灰色模糊综合评判模型在水利工程监理单位优选中的应用

李 增

(辽宁水利土木工程咨询有限公司，辽宁 沈阳 110000)

招投标作为工程监理单位优选的主要方式，对于发挥监理制在水利工程的作用，完善和优化工程监理市场并满足社会市场经济需求具有重要意义[1]。在施工招投标的基础上发展而来的监理招投标在程序上二者及其相似，然而在内容条件以及评标宗旨方面同样存在着显著的差异。在符合投标人要求的技术标准条件下注重考虑投标人报价水平为施工评标的核心和宗旨，其中各投保人的报价水平和施工能力通常是决定其能否中标的关键性因素。根据水利工程监理单位不需生产实质性的物质和监理评标的特殊性可将其评标宗旨归纳为“能力的选择”，主要是对投保人的技术水平与服务质量进行考察并评选出具有较高技术水平的监理团队，以科学合理的监督管理方式对工程各参建方进行监督并确保水利工程建设的环保、质量、进度、安全和费用达到既定目标和项目的顺利运行。然而，在监理项目评标时虽然不再以价格作为主要的判定依据，但仍需遵循“低价值差、优价优质”的市场规律[2]。

水利工程监理单位的评标其本质是对多个待评价对象，在多准则、多目标的条件下进行优选的过程，科学合理的评价指标体系和评标方法是决定评标工作公正、客观、科学的核心和主要内容。目前，综合评价法、摇珠原理以及最低评标价法等为传统的工程监理评标方法，其中综合评价法因具有考虑因素全面、适用性强以及能够充分发挥相关专家阅历经验和专业知识的优点而被广泛应用于监理优选评价，然而该方法透明度较低，且受人为主观性判断影响显著，因此极易引起腐败现象并造成评价结果有失公平、公正的原则；摇珠原理可简化投标程序、避免覆盖现象的出现并具有较高的透明度然而缺乏相应的则优原则且科学性较低；最低评标价法可符合市场竞争规律具有目的明确、操作简单、造价控制简便等优点，然而容易产生低价竞标和唯价格论，对各投标人的优劣、技术能力，无法客观、全面的体现[3]。灰色关联度分析法、模糊综合评判法、层次分析法、人工神经网络法以及数据包络分析法等是在现代决策理论的基础上发展而形成的方法，上述方法不仅可在工程监理评标领域提升人们的理论水平和知识认知，而且可有效解决传统决策方法的单一片面性问题，同时也可为评标的最终决策提供一定的指导和监理。然而，在赋权方面上述方法还存在一定的主观随意性，评价模型和指标体系仍需要进一步的完善和探讨。据此，本文结合已有研究成果和相关理论构建了指标体系，然后对各指标权重采用模糊层次分析法进行确定并基于组合集成的理论构建了模糊综合评价模型，以实际工程为例，对各监理单位运用评判模型进行优选评价[4]。

1 建立水利工程监理单位优选指标体系

结合相关历史资料以及工程监理的评标特点，本文在遵循指标前瞻性、可行性、系统性、相对独立性以及系统性原则的基础上构建了监理单位评价指标体系，见表1。

2 构建灰色模糊综合评价模型

2.1 模糊层次分析法

在构建判断矩阵时采用传统的AHP法通常会忽略人为判断的模糊性，从而降低评价结果的准确性与可靠性，运用模糊逻辑理论对传统的AHP法进行改进并形成模糊层次分析法可显著提高指标权重计算的精度[4]。引入F=(fij)m×m为判断矩阵并符合fi+fj=1，该矩阵即为模糊互补矩阵，若fij为0，则代表元素fj的重要性大于fi；若fij为1，则代表fj的重要性低于fi；若fij为0.5，则代表元素fj的重要性与fi相同。然后将矩阵F=(fij)m×m进行模糊一致性矩阵的转换，将矩阵每行进行求和计算，使其符合下式：

(1)

利用下式对其进行转换：

(2)

若矩阵符合Sij=Sik-Sjk+0.5，则可认为该矩阵满足模糊一致性检验，变换后的矩阵经过检验可认为满足条件。然后利用下式进行权重的求解，如下：

(3)

2.2 构建综合评价模型

考虑到评价对象信息的模糊性和灰色性特征，本文结合相关理论和分析方法构建了基于灰色关联度的模糊综合评判模型。根据评价对象各影响因素建立评价指标集，即U={U1,U2,U3,,Um}；然后对各指标利用模糊层次分析法进行求解并构造权重集，即W={W1,W2,W3,,Wm}；结合待评价水利工程监理单位的实际状况构建评语等级论域，即V={V1,V2,V3,,Vn}，从而构造模糊关系矩阵R，其表达式如下：

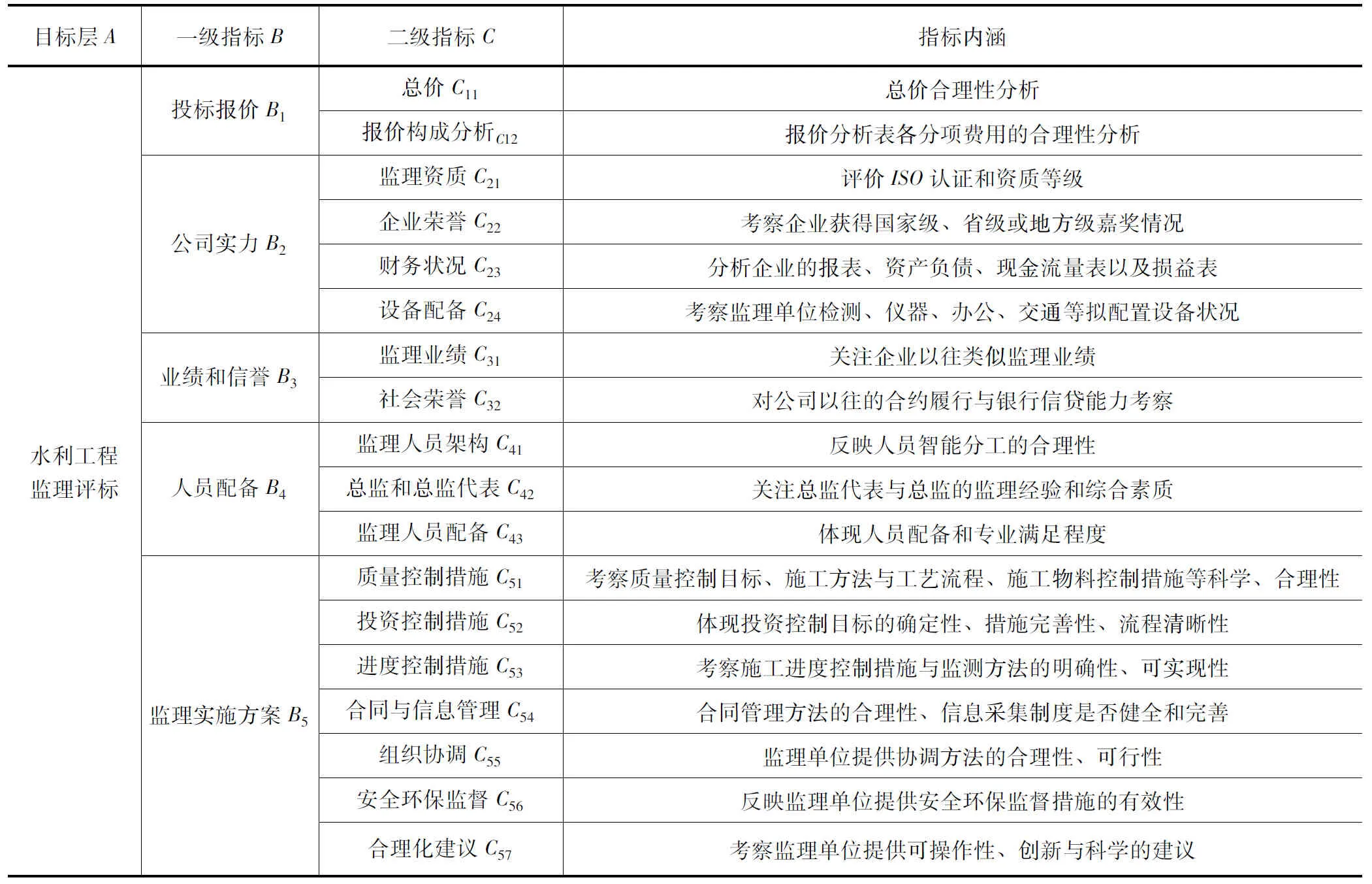
表1 水利工程监理评标的指标体系及内涵

(4)

式中,rij—在j评价等级下待评价对象对应于i评价指标的隶属度；本研究在考虑了专家意见以及相关文献资料的基础上确定了各评价指标的隶属度，即rij=t/T，其中t、T分别为对i指标评语等级在j的专家和评价专家的总人数。

然后利用公式Bi=Wi·Ri对各一级指标进行模糊综合评判，结合一级评判结果对各二级指标进行综合评判，二级指标计算公式为B=W·Bi。确定最优参数序列和比较数据序列分别为X0={X0(k)|k=1,2,3,,n}、Xi={Xi(k)|k=1,2,3,,n;i=1,2,3,,m}，则灰γ0i(k)色关联系数求解公式如下：

(5)

式中，ρ—分辨系数，其值为0.5。

比较序列相对于参考序列的灰色关联度采用γ(X0,Xi)表示，通常情况下对灰色关联度采用平均值法进行确定，并按照其值的大小进行排序，均值计算方法如下：

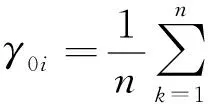
(6)

3 实例应用

本文以辽宁省某水利工程项目施工监理评标为例，利用所构建的模糊综合模型进行优选，该水利工程项目通过资格审查的监理单位共有甲、乙、丙、丁四家，评标委员会由专家库中随机抽取的10专家组成并对该水利工程项目进行评标[5]。结合该项目相关数据材料以及专家调查结果，对各评标指标进行两两对比分析初步确定重要性评比结果[6]，然后利用文中所述权重计算公式进行求解，结果见表2。评价等级分别为V1～V5，相应的评语为优秀、良好、中等、一般很差。然后根据专家组对各指标的评价结果可进行隶属度的计算，甲监理公司的隶属度计算结果见表2。

表2 各评标指标权重计算结果

然后根据隶属度计算结果可得到模糊关系矩阵，利用文中所述一级和二级模糊综合评判矩阵计算公式，可得到B1=(0.112，0.637，0.260，0.000，0.000)，同理可求得B2=(0.281，0.542，0.116，0.015，0.015)、B3=(0.778，0.112，0.112，0.000，0.000)、B4=(0.382，0.226，0.125，0.181，0.052)、B5=(0.331，0.486，0.106，0.042，0.022)。利用公式可分别求得各二级指标模糊综合评判结果，见表3。

表3 各监理单位各二级模糊综合评判结果

根据上述模糊综合评判结果按照隶属度原则，可认为四家水利工程监理投标单位均处于“良好”水平等级。据此，为更加准确、合理的优选出最佳监理单位，本文采用灰色关联度法，对4家监理单位作进一步的深入分析，首先对各指标数据按照公式进行标准化处理，结果见表4。

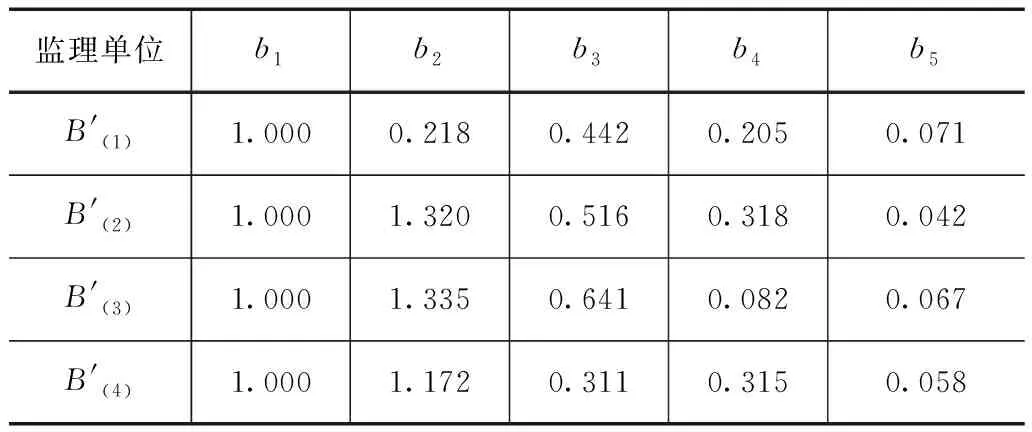
表4 灰色关联数值初始化处理

4 结语

(1)在评标指标权重确定中引入模糊层次分析法不仅避免了传统AHP法中的缺陷提高了权重的客观性与全面性，而且充分考虑了人为判断的模糊性特征，在一定程度上课简化计算过程和方法提高计算效率，并且所构造的判断矩阵无需对其一致性作进一步的检验，权重计算结果更加符合监理公司实际情况。

(2)对水利工程项目的各监理投标单位利用灰色模糊综合评价法进行客观、系统的评估，不仅避免了有效信息丢失的现象，而且利用最大隶属度原则进行评价提高了评价结果的合理性与真实性，评价结果更加科学合理，对于优选出技术水平较高、服务质量较好的水利工程监理单位具有重要意义。

(3)在水利工程监理投标优选过程中采用该评价模型具有一定的参考价值和指导意义，通过对理论方法的稍加改动还可用于决策方案的优选中，在水利工程监理该方法具有广泛的应用价值和显示意义。