改进的蓄水曲线法在平原区排涝模数计算中的应用与分析

孙 娟

(辽宁省水文局，辽宁 沈阳 110003)

排涝模数的合理确定对于平原区排水泵站的合理规划及防洪排涝规划至关重要，当前，对于平原区排涝模数的研究方法较多，大致可分为3种：经验方法[1-3]、水量平衡方法[4-6]以及河网水动力学模型方法[7-9]。经验方法大多需要当地进行观测试验，结合试验数据进行统计得到平原区的排涝模数计算经验方程，这种方法存在区域适用性，很难进行普及应用。水量平衡方法理论性较强，其中蓄水曲线方法即为水量平衡方法的一种，这种方法较为适合平原排涝区水系较为简单的区域，而对于水系较为复杂的区域，该方法的适用性较差。对于水系较为复杂的平原区域，主要采用河网水动力学模型方法进行计算。近些年来，蓄水曲线方法由于计算原理较为简单，在平原区排涝模数计算中应用较为广泛，但是传统蓄水曲线方法由于未能考虑排涝区的调蓄作用，存在一定的局限性，为此本文引入改进的蓄水曲线方法，以辽宁中部平原区为研究实例，对比不同算法下区域排涝模数的计算精度，分析改进算法的适用性，并定量分析平原区排涝模数计算的主要影响因子。

1 研究方法

在平原区排涝模式的主要计算方程为：

(1)

改进的蓄水曲线方法将平原排涝区看成是一个蓄水水库，做出水库蓄水变化曲线，结合水库调蓄方式寻求较为稳定的调蓄库容，其调蓄水位主要计算方程为：

(2)

式中，St—不同时刻计算蓄水点的排涝面积，km2；H—蓄水的节点水头，m；∑Qt—蓄水节点水量，m3。

当为自由出流时，其蓄水节点水量的计算方程为：

(3)

式中，m—自由出流比例因子；B—排涝区蓄水节点溢流宽度，m；Zu—其上游观测水位，m；Zd—其下游观测水位，m。当其出现淹没出流时，其计算方程转变为：

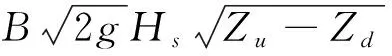
(4)

式中，Hs—排水区平均水位，m；其他变量含义同式(3)中变量含义。

2 研究成果

2.1 区域概括

本文以辽河东岸盘锦混合区为研究实例，盘锦市境内辽河以东、大辽河以西由北向南沿盘山县吴家乡和大洼县新立镇、田家镇、清水镇、王家镇中轴线构成此混合区。区域面积为753.7km2。主要河流有螃蟹沟、六零河、清水河排干、赵圈河排干、干鱼沟、接官厅排干、五岔河、西海河等8条。其中一级支流5条，二级支流2条，三级支流1条。结合区域内赵圈河排干实测排水量数据，对比分析改进前后的蓄水曲线方法在平原区排涝模数计算的适用性。

2.2 排涝模数计算精度对比

分别采用改进前后的蓄水曲线方法对研究区域的排涝模数进行计算，在区域排涝模数的基础上，结合区域面积获得区域排涝水量，为对比不同算法下排涝模数的计算精度，基于不同算法下的排涝水量与区域实测排涝水量进行对比，对比结果见表1。

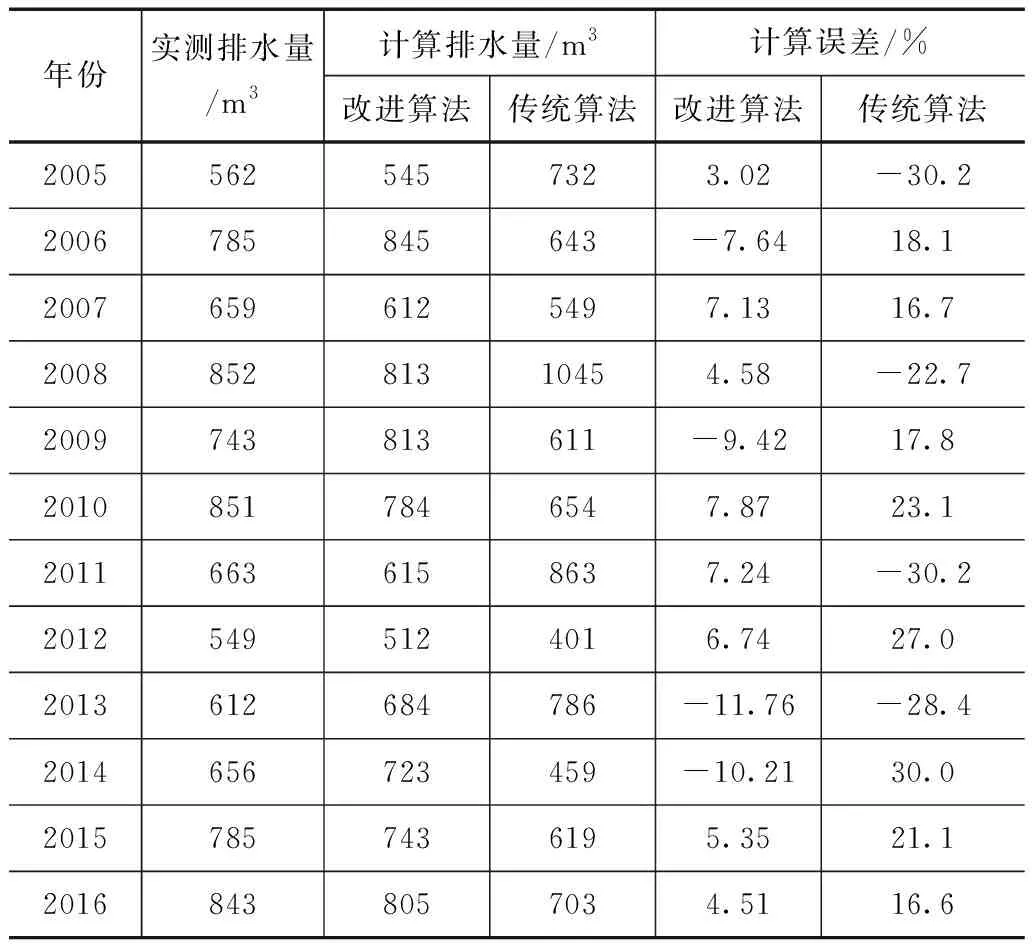
表1 不同算法下排涝量计算精度对比结果

从表1中可以看出，改进算法下区域的排涝水量计算误差均小于改进前的计算误差，相比于传统蓄水曲线算法，改进后的算法下，其计算精度平均提高16%，这主要是因为改进后的蓄水曲线方法综合考虑平原排涝区的调蓄作用，增加调蓄影响因子，基于区域水量平衡计算下的排涝模数更为合理化，相比于传统蓄水曲线方法，排涝模数更为精确，也使得区域排涝水量计算误差减少。

2.3 主要影响因子分析

为定量分析平原区排涝模数主要影响因子，结合改进的蓄水曲线计算方法，定量分析不同排涝面积倍比下的区域排涝调蓄量以及不同过水断面面积下的区域排涝水量，分析结果见表2—3、如图1所示。

表2 区域排涝调蓄量～排涝面积倍比变化关系

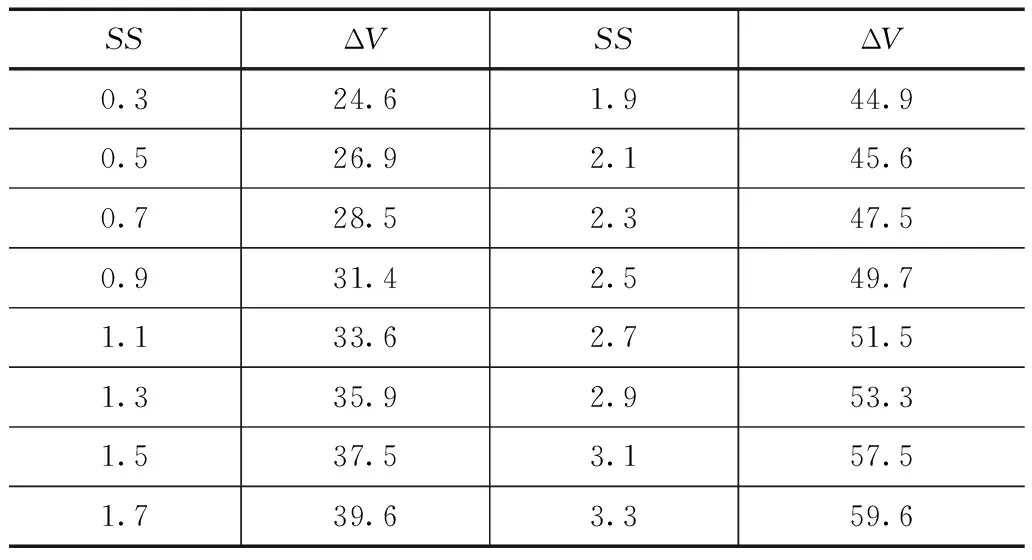
表3 区域排涝调蓄量～过水断面面积倍比变化关系

图1 排涝调蓄量与主要影响因子关系图

从表1和表2均可看出，区域排涝调蓄水量和排涝面积倍比及过水断面面积之间呈现较好的正向变化，随着排涝面积倍比的增加，区域调蓄水量也逐步增加，而过水断面面积增加后，区域的排涝调蓄量也稳步增加，从图1中也可直观的看出排涝调蓄量和这两个主要影响因子之间的正向线性变化关系。可见，对于平原区排涝调蓄量影响的两个主要因素为排涝面积倍比AA以及过水断面面积比SS两个因子。

2.4 影响要素综合分析

在主要因子分析的基础上，综合分析两要素同时变化对区域排涝调蓄量的影响，综合影响分析结果见表4。

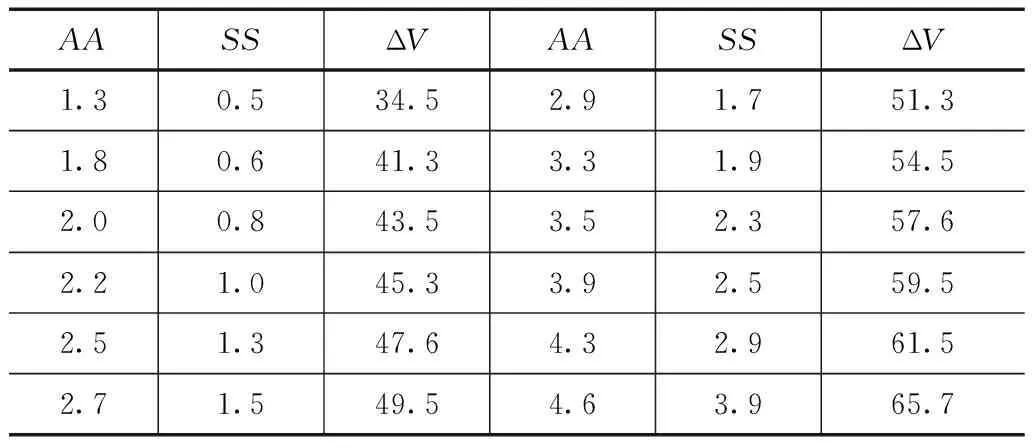
表4 区域排涝综合影响分析结果

从表4中可看出，区域排涝调蓄量和区域排涝调蓄两个主要因子呈现指数变化关系，增大区域排涝能力可以适当增加区域的过水断面面积，而对于过水断面面积比较难增加的区域，可以通过调整区域的排涝面积倍比来增加区域的排涝模数，从而提

高区域排涝水量以及排涝效率。从表中还可看出，平原排涝区过水断面面积的影响要大于区域排涝面积倍比的影响度。

3 结论

本文结合改进的蓄水曲线方法对辽宁中部平原盘锦混合区的排涝模数进行计算，并定量分析其影响主要因子，分析取得以下结论：

(1)改进的蓄水曲线方法下的排涝模数计算误差明显改善，但对于水系较为复杂的平原区域，该方法适用性不如水动力学模型，对于水系较为简单的平原排涝区适用性较高。

(2)在平原区排涝整治规划中，可通过适当调整区域过水断面面积比以及排涝面积倍比来提高排涝模数，排涝面积倍比的影响度低于过水断面面积比。