基于多周期的危险品多式联运路径优化研究*

李 萍,朱宗良,苌道方

(上海海事大学 物流科学与工程研究院，上海 201306)

0 引言

根据国家统计局统计，2017年我国多式联运货运量约17.47亿t，占全社会货运量的4.1%，其中危险品多式联运货运量约2亿t，占比约为16.5%。2020年，我国多式联运货运量预计将达到30.28亿t，复合增长率为20.11%[1]。危险品货运量增加的同时，也给危险品运输带来了挑战，研究危险品多式联运路径优化问题具有重要意义。

目前，国内外学者对危险品多式联运已经有了一些研究。魏航等[2]将运输网络进行变形,建立了在时变网络条件下多式联运有害物品的最短路径模型，并利用Dijkstra算法求解出不同出发时间下的有效路径；叶炽球[3]在此基础上，考虑时变条件对危险品运输社会恐慌度的影响，构建时变条件下有运量限制的危险品道路运输最短路径模型；张得志等[4]建立了时间和路段能力约束的最短路径模型，并用启发式算法求得多城市间多种运输方式的最佳组合；开妍霞等[5]以事故损失及运输成本线性加权和最小为目标，对危险品运输网络中的运输方式和路径优化开展研究；黄丽霞等[6]以总成本和总风险最小为目标，建立双目标0-1线性规划模型；Xie等[7]研究了危险品多式联运的选址-路径问题，建立了1种多目标、多模式的混合整数线性规划模型；辛春林等[8]以成本和风险的加权和最小化为目标建立了配送选址—多式联运路径优化模型;辛春林等[9]基于运输费用和人口风险的较强时变特性,建立危险品多式联运的最短路径选择模型，利用Dijkstra改进算法进行求解;Manish Verma和Ghazal Assadipour等[10-13]在多式联运的基础上，考虑风险因素，建立风险模型。从以上文献可以看出，关于危险品多式联运的研究都是使用单周期模型进行终端选址和路径优化，而危险品运输具有较强时变的特性，因此本文考虑在动态网络下，选择多周期模型进行路径优化。

本文基于由多个路径期组成的危险网络进行规划研究，以降低运输成本及风险(伤亡人数及财产损失)为目的，建立1个混合整数概率鲁棒模型，并通过模拟退火算法求解，达到在不同场景及周期内多式联运终端位置和运输路线同时优化的目的。

1 模型构建

1.1 问题描述

本文研究了危险品多式联运网络扩张问题，在网络规划期间，某一路径起止点(Origin Destinatinpair, OD对)之间的运输路线上可能包含多个多式联运终端，并将规划期T划分为1组短时间段即路径期，用于路径决策，同时这些时段的1个子集Tl进行扩张决策，且在每1个扩张期以及在预算范围内开放新终端，扩容已有终端或者重铺铁路。由于受到自然或人为因素的影响，网络终端和链路中断的风险具有不确定性，且存在发生中断的概率，这些中断会很大程度降低终端及链路的运输能力，以及对人口密集且短时间内不易疏散的脆弱区域造成人口伤亡和财产损失，当受影响的终端及链路逐渐恢复能力时，其将再次成为最优路径。多周期的规划问题可以概括为在每个扩张期预算有限的情况下确定需要改进的路径期。本文做了以下假设：在每个扩张期开放的终端在规划期内一直保持开放;扩大终端的容量在规划期内不会减少;各终端及路径上的成本和风险已知;各场景下的终端及链路中断风险是相互独立的;中断只发生在扩张期，受损的终端及链路从路径期中逐渐恢复，直到下一个扩张期完全恢复。

1.2 符号说明

1)集合含义：

2)参数含义：

3)决策变量含义：

1.3 模型建立

minC期=μC+(1-μ)R

(1)

(2)

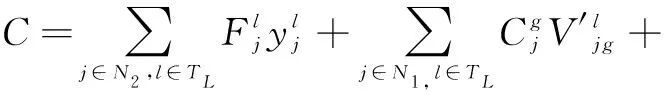
(3)

(4)

s.t.

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

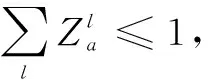
(13)

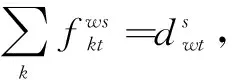
(14)

(15)

(16)

(17)

式(1)为目标函数,表示期望成本最低，其中μ为运输危险品的成本权重(假设μ为0.6)，(1-μ)为风险权重；式(2)表示危险品风险函数，包括运输风险和转运风险；式(3)表示危险品的成本目标函数，包括开放终端成本，扩容终端容量成本，铁路重铺成本，运输成本和转运成本；式(4)表示运输风险，其中β1和β2分别为人口风险和财产风险的权重；式(5)和式(6)表示确保已有终端的容量在所有路径期内都多于路径上的货流；如果终端在以后的特定场景下保持弹性，则激活式(5)，否则使用式(6)；式(7)表示确保危险品在公路中的货流不超过其链路的能力；式(8)表示确保新开放的终端容量在所有路径期内都多于路径上的货流；式(9)和式(10)表示确保危险品在铁路中的货流不超过其链路的能力，与式(5)和式(6)类似，如果在特定场景下链路保持弹性，则式(9)被激活，否则式(10)被激活；式(11)表示确保最多可以为已有终端选择1个容量模块;式(12)表示确保备用终端在所有扩张期内最多可以打开1次；同理，式(13)表示保证每条铁路链路在扩展周期内最多进行1次重铺；式(14)表示确保OD对间的供需平衡；式(15)表示确保货流分配给开放的终端；式(16)表示在扩张期内成本不能超过预算；式(17)表示决策变量非负。

2 模型求解

1)将可行解编码为1个单维数组。每个数组由2个部分组成，分别用于寻找备用终端和铁路重铺决策以及在扩张期扩容已有终端的容量。通过该算法生成1个随机初始解，并对其在式(16)条件下的可行性进行验证，当决策变量确定下来时，问题就变为单一场景单一路径期下的多式联运路径规划问题。当路径子问题得到解决时，则开始计算目标函数。

步骤1：选择1个决策变量x(备用终端，链路或已有终端)和随机路径期t。

步骤2：

①如果x是备用终端且x的对应值等于t，则有：当在t周期备用终端没有开放时，计算成本/容量的值，最低值的终端在t周期开放且x在整个规划期间关闭。当在其他周期没有终端被开放，则关闭x，且在t周期没有终端被选择打开；当在t周期备用终端开放时，则计算成本/容量的值，在整个规划期内关闭最高值的终端，并且在t周期开放x；如果在t周期没有新的终端开放，则在这个周期x将一直开放。

②如果x是现有的终端,则有：在t周期将x的容量模块随机更改为与其可用模块不同的1个模块；在t周期把x和随机已有的终端y容量模块进行交换。

③如果x是铁路则与①同理。

步骤3：检查新解是否在预算范围内。如果不在，则舍弃并转到步骤1。

2)当生成可行解，则在所有的路径期内把货流分配给整个网络并计算此时的目标函数值C(γ)。C(γ0)为初始的目标函数值，如果C(γ)≤C(γ0)，则接受新解C(γ)。否则，是否接受这个非改进解由Boltzman函数e＾(-Δ/φ)决定，其中φ为当前温度，Δ是C(γ0)和C(γ)之差。随机产生1个∂∈[0,1]，当∂≤e＾(-Δ/φ)时，则接受这个非改进解；反之则不接受。如果C(γ)仍小于非改进解，则C(γ)为目前的最优值。

3)在每个温度下产生并计算领域解的范围K。对K进行计算后，其温度随φ(i+1)=Ω×φi函数的变化而减小,Ω是当温度下降时的冷却速率，且Ω∈[0,1]。设φ0为冷却时的温度，当φi≤φ0时，或者当设定的迭代次数中没有最优解，则算法停止。

3 算例分析

图1为随机网络,图中的数字为对应编号。给出了12个城市、4个已有终端、2个备用终端、2个扩张期和7个路径期。本算例采取2个扩张期，分别在第1年和第4年开始进行扩张决策，每个扩张期分别有3个场景，第1个扩张期的3种场景分别为:①随机网络有60%的概率不会发生中断；②终端4有30%的概率发生中断；③与城市12相连的所有链路出现中断的概率为10%。第2个扩张期的3种场景分别为：①随机网络有75%的概率不会发生中断；②终端6有20%的概率会发生中断；③与城市3相连接的所有链路出现中断的概率为5%。在扩张期内发生概率最高的第1个场景为随机网络中没有发生中断，即为正常情况，飓风和冰雪灾害是第1个扩张期的另外2种场景；龙卷风和洪水是第2个扩张期的另外2种场景。每个中断场景在其相应的扩张期开始时损坏程度最大，并且其严重程度随着时间的推移而减少。本文算例在Python环境中进行求解。

3.1 多周期规划方法对联运网络的影响

本文将单周期规划方法与多周期动态规划方法进行比较，并分析了2种方法对总运输成本的影响。单周期规划方法同时考虑了多周期中不同时期的所有OD对，并假设在所有情况和时间段内终端及链路中断达到最大百分比，并通过计算得出最优方案，即在规划期开始时开放备用终端5，扩容终端1和终端4并重铺了终端4—终端3以及终端1—终端4的2条铁路。与单周期相比，多周期危险品货运网络的最优方案为：在第1个扩张期扩容终端1，在第2个扩张期开放终端3以及扩容终端4，并且不进行铁路重铺。因此，与多周期规划

图1 随机网络Fig.1 Random network

方法相比，单周期的总运输成本在整个规划期内约为1 312万。而在相同的情况下，多周期在整个规划期内总运输成本约为726万，总成本降低了55.3%。

由于多周期规划是动态的，决策方案在不同的时间段内进行，且在所有路径期内中断的概率相对较小，而单周期规划方法忽略了随着时间的推移，危险品网络终端从中断到逐渐恢复这一过程和链路可能发生中断的低概率情况，当终端重新获得初始容量时，更多的货物可以通过成本最低的路径运输，而这一过程只能在多周期的动态模型中考虑，所以在多周期规划下没有预算用在重铺铁路上。结果表明，大部分的预算用在了扩容已有的终端上，而不是开放新终端以及重铺铁路上，因此多周期的总运输成本低于单周期的总运输成本。表1为随机网络参数的取值，服从正态分布。

表1 随机网络参数Table 1 Random network parameter

3.2 多周期规划方法对路径决策的影响

在多周期动态模型求解出的最优方案基础上，分析了第2个扩张期第2种场景下OD对(1～12)的路径结果。图2为第2个扩张期第2种场景下的路径,图中数字、图形与图1一致。如图2所示，虚线链路为运输成本和风险成本之和最小的路径。由于受龙卷风的影响，终端6初期能力下降了80%，在第2个扩张期的第1年，即第1个路径期，只有20%的终端容量可用于危险品运输，因此，只有20%的危险品通过虚线链路进行运输，其余80%的危险品则由其附近另一条成本较高的路线来运输，即通过终端2所在的双箭头路线进行运输；在扩张期的第2年，即第2个路径期，终端能力逐渐恢复，其容量的60%可以进行危险品的运输，因此，60%的危险品通过最短路径进行危险品的运输，其余40%的危险品由图中双箭头路线进行运输，同时扩容终端4以及开放终端3；在扩张期的第3年，即第3个路径期，终端6的能力完全恢复，全部危险品由虚线路径进行运输，在第4个路径期与第3个路径期一致，具体情况如表2所示。

图2 第2个扩张期第2种场景下的路径Fig.2 The path under scenario 2 in the second expansion period

t路径货流/%1城市1—终端1—终端4—终端6—城市1230城市1—终端1—终端2—城市3—城市8—城市12702城市1—终端1—终端4—终端6—城市1260城市1—终端1—终端4—终端3—城市12403城市1—终端1—终端4—终端6—城市12100 4城市1—终端1—终端4—终端6—城市12100

此外，本文还分析了预算和转运成本对总成本及路径货流的影响，如表3所示。一方面，预算对总成本及路径货流有较高的影响。当预算增加时，运输路径中的货运流量将增加10%，同时总成本会降低；相反，当预算减少时，货运流量会减少且总成本显著增加。当减少预算时，开放终端的数量以及扩容终端的规模将变小，从而较经济的路线运输能力将减少，导致货物只能通过其他高成本的路线运输，进而增加了总运输成本；同理，当预算增加时，在规划期内可以开放和扩容更多的终端，增加经济路线的运输能力，降低成本。另一方面，转运成本对总成本及路径货流的影响较低。当转运成本增加时，总成本略有增加但是货运流量保持不变；当转运成本减少时，总成本略有降低并且货运流量略有增加。由于终端上的转运成本降低，总成本也随之降低，路径将变得更经济，因此会有更多的危险品通过该路径进行运输；而转运成本增加，会带来总成本增加。

表3 灵敏度分析Table 3 Sensitivity analysis

4 结论

1)针对危险品多式联运网络扩张问题，考虑了成本及风险因素，并将风险进行量化处理以经济损失的形式表现出来且赋以权重进行加和，最后，以总成本以及风险最低为目标，建立混合整数概率鲁棒模型，在模型中将扩张决策和路径决策的不同时间段相结合。

2)以小型随机网络为算例，利用模拟退火算法进行求解，解决了公铁联合货运网络扩张问题，得出危险品在不同时间段的运输方案；通过对特定场景下其中1组OD对路径进行分析，验证了模型的合理性。

3)考虑建立时间窗下多周期的危险品联合货运实际网络模型，以及研究不同权重对路径的影响是未来研究的方向。