城市轨道交通列车大小交路开行方案优化

刘 意，陈 东

（西南交通大学 交通运输与物流学院，四川 成都 610031）

0 引言

在断面客流空间分布不均衡程度较高的城市轨道交通线路上，采用合理的列车大小交路开行方案，在保证必要的服务水平前提下，达到节省车辆数量，加速车辆的周转，提高运营效益的目的[1]。

针对城市轨道交通列车大小交路开行方案的研究，主要是确定理想的列车开行数量及范围、行车间隔、编组数等。王媛媛等[2]以乘客在途与等待时间成本、车辆配置费用与车辆走行费用最小为目标，建立双目标非线性整数规划模型。许得杰等[3]将列车编组数加入决策变量，允许不同交路区段采用不同的编组形式，并把多目标约束优化模型转换为单目标无约束优化模型求解。田晟等[4]将乘客出行时间价值和平均载客率作为目标函数，用以体现运营服务质量和运力利用水平，并采用粒子群算法求解多目标优化模型。王永岗等[5]运用RailSys仿真软件为优化模型标定了不同交路区段中列车的运行时分、速度等相关参数，并利用隶属度函数求得模糊最优解。

运用车数是影响列车大小交路开行方案决策的重要因素之一，可以通过列车运行图周期与行车间隔求解。目前对大交路区段和小交路区段中列车运行图周期的确定，大多采用列车往返旅行时间加折返站最短折返时间的方法。在该方法下即便折返站能力满足要求，也会由于不同交路区段中列车在公共区段共线运行，造成列车间的相互制约。为保证不同交路区段中列车合理的开行比例和均衡的行车间隔，列车折返时间往往会大于最短折返时间，从而导致列车运行图周期呈现规律性变化[6]。因此，针对仅一个中间折返站的列车大小交路开行方案，采用“运行图周期分析法”来确定列车运行图周期，从而建立列车大小交路开行方案优化模型，并使用Lingo进行求解。

1 问题描述及参数定义

列车大小交路开行方案如图1所示，其中S ={sj|j= 1，2，…，n}为车站集合，se为中间折返站e∈(1，n)；se至sn之间为非小交路区段，记做H1，s1至se之间为小交路区段，记做H2，该区段为线路上断面客流较为集中的区域，H1与H2共同构成大交路区段；Tk为第K个运营时段时长；aij为Tk内出行起点为i，讫点为j的客流量；根据出行起讫点的不同，可将客流分为4类，①类、②类为下行方向客流，③类、④类为上行方向客流，①类、③类客流出行起讫点均在H2区段，②类客流出行讫点在H1区段，起点不限，④类客流出行起点在H1区段，讫点不限；tj为列车在s1至sj间的往返旅行时间；Tk内开行在大交路区段(H1与H2区段)的列车数量和列车编组数分别记做f1，q1，仅开行在小交路区段(H2区段)的列车数量和列车编组数分别记做f2，q2。

图1 列车大小交路开行方案Fig.1 Long and short routing train plan

列车大小交路开行方案车底周转模式如图2所示。

图2 列车大小交路开行方案车底周转模式Fig.2 Fleet turnaround modes of long and short routing

理想状态下大交路区段中列车最小运行图周期Tzdmin计算公式为

式中：tn，tzmin分别为大交路区段中列车往返旅行时间和折返站最短折返时间。

令H1区段与H2区段行车间隔分别为I1，I2。根据列车运行图周期理论，为保证各区段行车间隔的均衡，减少运行图空费时间，I1通常为I2的整数倍，即小交路区段中列车开行数量为大交路区段中列车开行数量的整数倍[6]。当采用以大交路区段中列车最小运行图周期为基础来确定小交路区段中列车周转方式的车底运用模式时，如果0，则计划的行车间隔I1，I2均不能实现。为解决该问题，可以按以下公式对大交路区段中列车运行图周期进行调整。

由于不同交路区段中列车在H2区段共线运行，列车间相互制约，将导致小交路区段中列车在中间折返站的折返时间有所增加，其列车运行图周期的计算公式为

式中：m∈Z+，m的取值与γ有关[6]。

式中：γ为小交路区段与大交路区段中列车往返旅行时间的比值；te为小交路区段中列车往返旅行时间。

m取值[6]如表1所示。

表1 m取值Tab.1 Values for m

2 模型建立

从乘客和运输企业出发，以乘客出行成本和企业运营成本最低为模型优化目标。

2.1 基本假设

（1）列车均采用“站站停”模式，同一区间范围内列车上、下行旅行时间相同。

（2）研究时段内乘客均匀到达车站，并选择第一列直达列车出行，无滞留乘客，无不同交路间换乘客流。

（3）大交路区段和小交路区段中列车车底独立运用。

（4）所有折返站列车折返间隔时间不超过线路允许的最小追踪间隔时间。

（5）同一交路区段中列车编组数一致，不同交路区段中允许不同的列车编组数。

2.2 乘客出行成本

乘客出行成本主要包括乘车费用和出行时间成本等。乘车费用由乘客出行起讫点距离决定。乘客出行时间主要包括在站候车时间、在车纯运行时间和途中停站等待时间[2]。根据基本假设（1），在车纯运行时间仅与乘客出行起讫点相关。停站时间除个别集散量特别大的车站外，各站并无太大差异。综上所述，在站候车时间更能体现不同列车开行方案间的差异，宜作为乘客出行成本。

根据基本假设（2），第②、第④类客流仅选择大交路区段中列车出行，第①、第③类客流可选择大交路和小交路区段中列车出行。单位乘客在站平均候车时间趋近于行车间隔的一半。乘客在站候车时间最小化目标Z1为

2.3 企业运营成本

企业运营成本可分为固定运营成本和可变运营成本。固定运营成本可根据运用车数确定。大交路区段运用车数Nd、小交路区段运用车数Nx的计算公式分别为

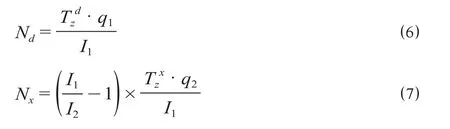
运用车数最小化目标Z2为

可变运营成本与列车开行距离及客位数量有关。考虑到城市轨道交通运输的公益属性，只将虚糜的运能，即未被利用的客位公里计入可变运营成本。总供给的客位公里记做λ1，已被利用的客位公里记做λ2。

λ1为大交路区段、小交路区段中列车分别供给的客位公里之和，计算公式为

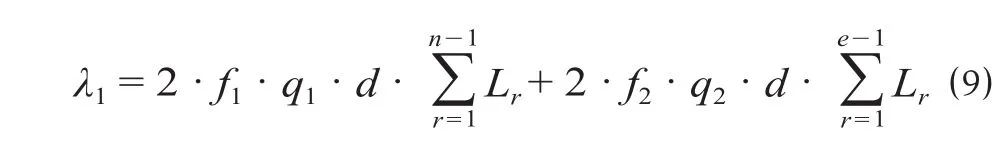
式中：Lr为第r个区间的长度分别为大交路区段、小交路区段的长度；d为车辆定员。

λ2通过上、下行方向上各断面客流量与站间距乘积之和求得，计算公式为

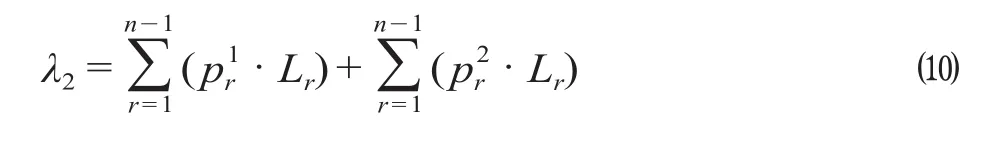
式中：pr1，pr2分别为线路上、下行方向上第r个区间(sj至sj+1之间，j=r)的断面客流量，计算公式为

虚糜运能最小化目标Z3为

2.4 约束条件

小交路区段与大交路区段中列车开行数量应满足整数倍关系，则有

Tk内I1，I2与f1，f2的关系分别为

令Imin为线路通过能力水平允许的列车最小追踪间隔时间，则计划行车间隔应满足令f1

min为在保证必要的设计满载率前提下，满足H1区段最大断面客流量需开行的最小列车数量，β为设计满载率，计算公式为

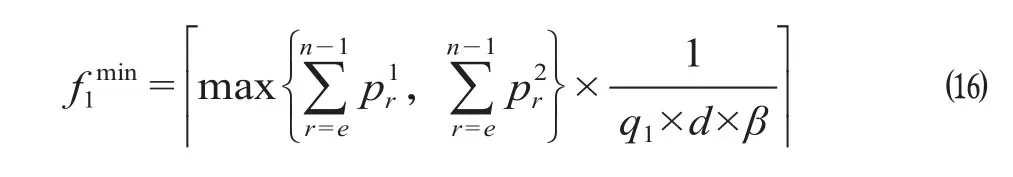
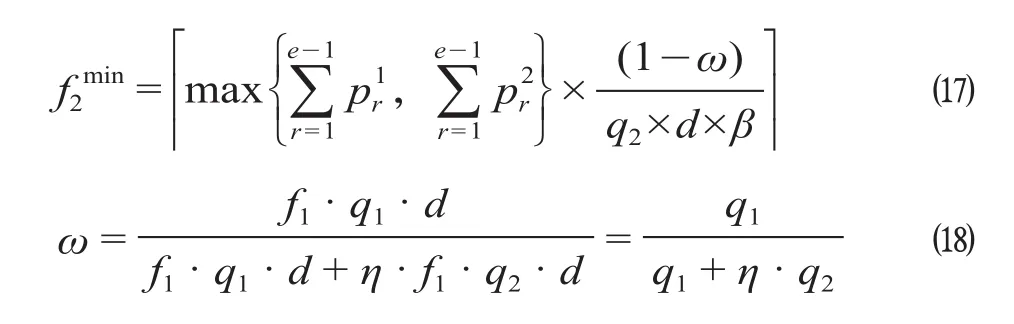
大交路区段、小交路区段中列车计划最小开行数量应分别满足

令Imax为为保证必要乘客服务水平而允许的最大行车间隔，则计划行车间隔应满足

令qmax，qmin分别为列车编组数的上、下限，则列车计划编组数应满足

此外，以下参数还应满足正整数约束条件

2.5 求解方法

该优化模型为多目标非线性混合整数规划问题。由于各优化目标均与成本相关，可将其换算成总成本，将多目标规划转化为单目标规划，如公式(24)所示，并用Lingo软件求解该模型。

minC=θ1·Z1+θ2·Z2+θ3·Z3(24)式中：C为总成本，元；θ1为乘客在站候车时间成本，元/min；θ2为每辆车投入的与走行公里无关的固定运营成本，元/辆；θ3为每客位公里可变运营成本，元/人公里。

3 算例分析

3.1 基础数据

某城市轨道交通1号线是一条连接城市核心区域与周边区域的半径线。全线有s1，s2，...，s14共计14个车站，站间区间依次编号为1，2，…，13。s1同时为大交路区段、小交路区段的端点折返站，s5，s8，s10，s12为具备折返条件的中间折返站。早高峰小时站间客流如表2所示。早高峰小时断面客流如图3所示，该时段客流具有明显的向心性特征，断面客流呈现“半钟型”[7]，符合线路走向及时段特点。各区间长度和旅行时间如表3所示，相关参数取值如表4所示，其中θ1，θ2，θ3的取值可参考文献[8-9]。

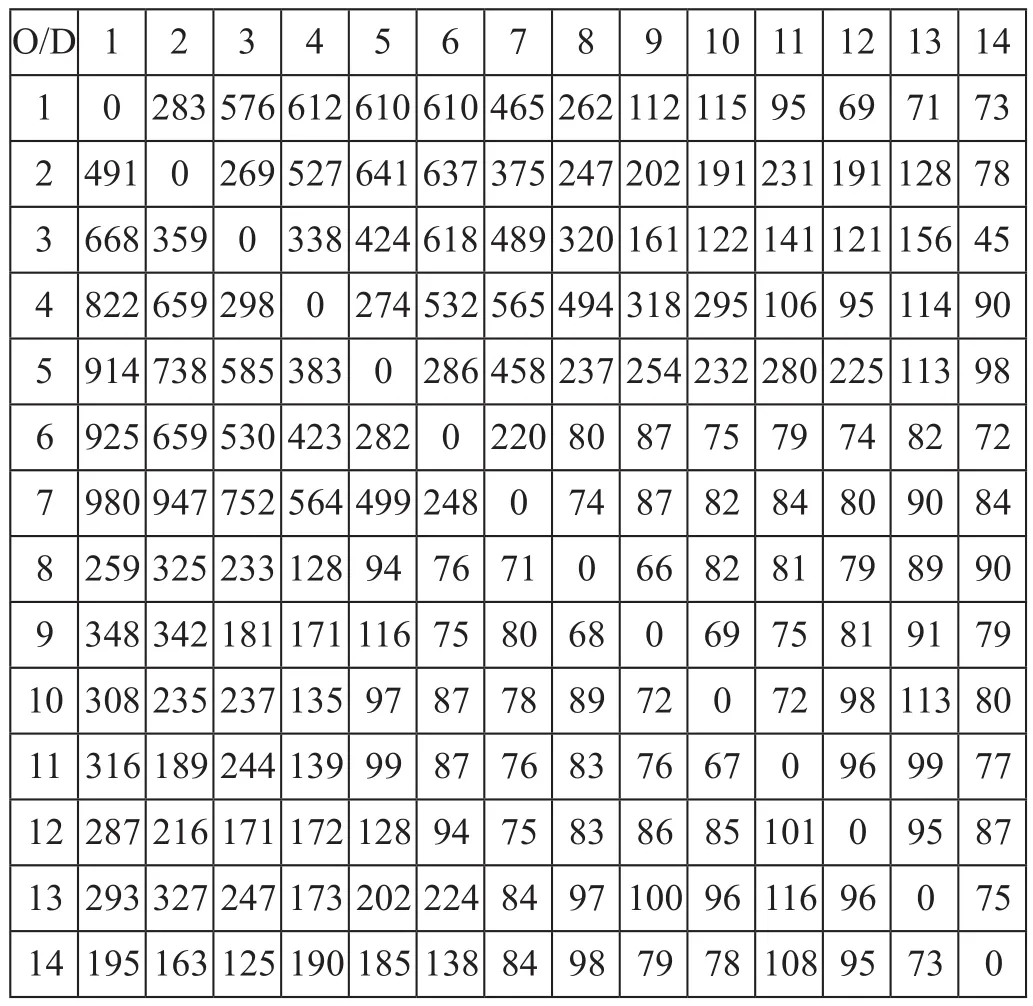
表2 早高峰小时站间客流 人次Tab.2 Passenger volume between stations during morning peak hours person-time

图3 早高峰小时断面客流Fig.3 Section passenger volume during morning peak hours

表3 区间长度和旅行时间Tab.3 Station spacing and travel time

3.2 算例结果

利用Lingo软件分别求解不同中间折返站条件下对应的最优列车大小交路开行方案。为便于对比，同时求解了单一长交路即列车常规交路开行方案的相关指标。各方案指标计算结果如表5所示。

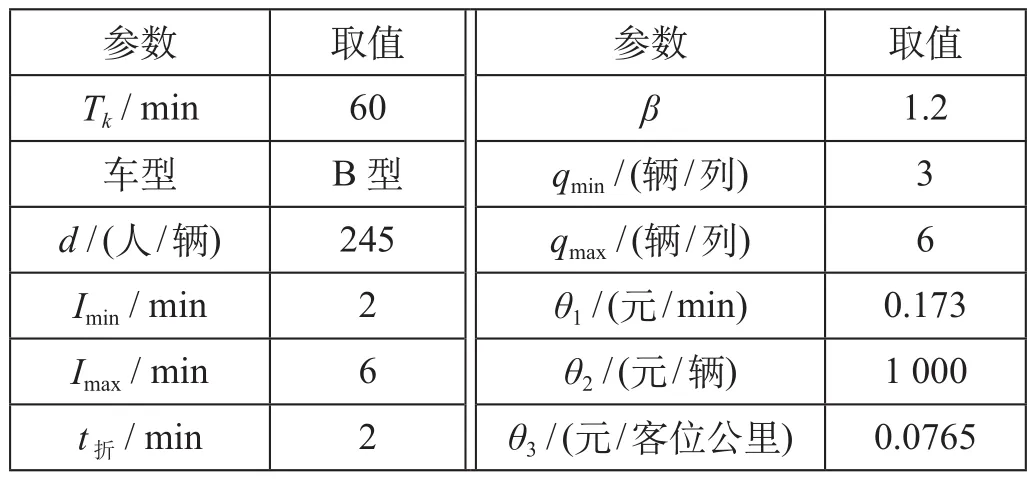
表4 相关参数取值Tab.4 Values for related parameters

3.3 结果分析

在表5中，方案Ⅰ至方案Ⅳ分别为4个不同中间折返站对应的最优列车大小交路开行方案，方案Ⅴ至方案Ⅷ分别为采用3 ～ 6辆编组的列车常规交路开行方案。2类列车交路开行方案中总成本C最低的方案Ⅱ相较于方案Ⅴ，其乘客出行成本θ1·Z1增加31.65%，固定运营成本θ2·Z2下降11.11%，可变运营成本θ3·Z3下降39%，总成本C下降9.75%，总运营成本下降18.21%。因此，以s8为中间折返站的方案Ⅱ为最优方案。在最优方案中，小交路区段覆盖了断面客流最为集中的线路区域，中间折返站选定在断面客流突变明显的区域附近。通过实例分析，验证了优化模型的可行性与有效性。

4 结束语

基于列车运行图周期分析法的列车大小交路开行方案优化模型，在兼顾乘客服务水平和企业运营成本的前提下，对以“半钟型”为典型客流空间分布特征、从城市核心区域向周边区域放射的轨道交通线路(半径线)，能给出较为优化的列车开行方案，但对另一种常见的以“凸字形”为典型客流空间分布特征、穿越城市核心区域的轨道交通线路(直径线)的列车开行方案，上述模型尚不能有效优化，后续研究中可继续针对此类线路进行建模优化。在原模型基础上，新优化模型需同时考虑小交路区段2个中间折返站的分布，并重新归纳在大交路区段、小交路区段中列车共线制约下列车运行图周期的变化规律，此外，列车停站模式作为开行方案的重要组成部分，有必要在“站站停”模式之外，将适用于列车大小交路开行方案的“区段停”模式纳入考虑范畴，以实现更好的优化效果。

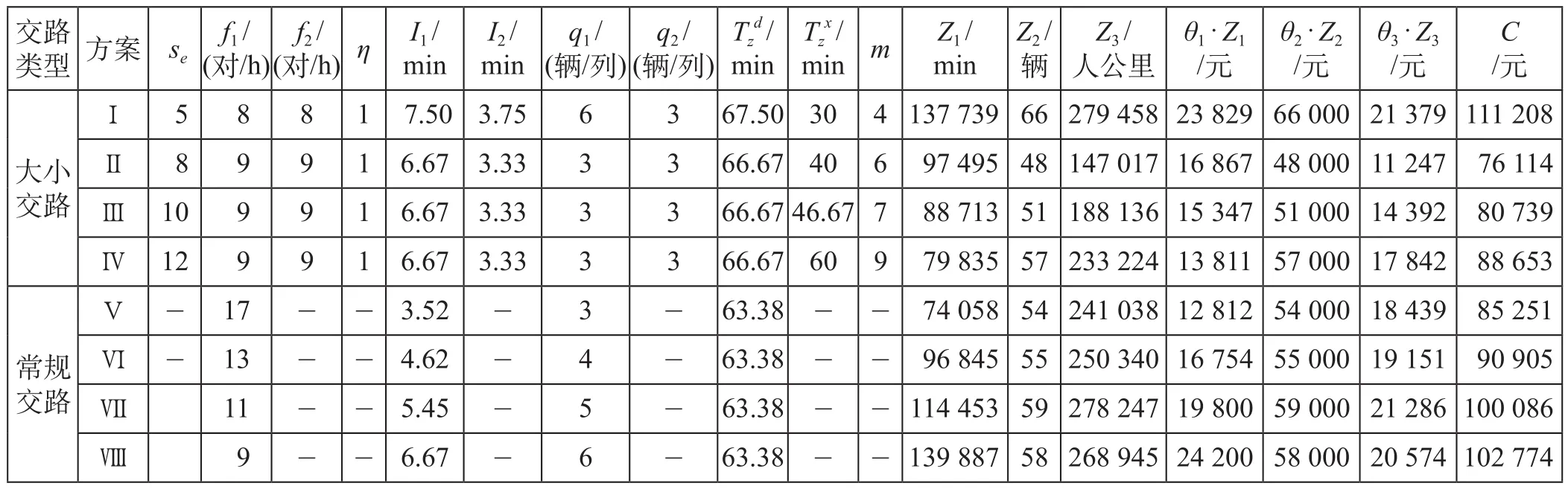
表5 各方案指标计算结果Tab.5 Parameter calculation results of various plans