拖拉机后悬挂横向位姿调整的模糊PID 控制
邵明玺,辛 喆,江秋博,张延安,杜岳峰,杨后富
(1. 中国农业大学工学院,北京 100083; 2. 潍坊科技学院,潍坊 262700)
0 引 言
作为粮食、油料的主要产地,中国丘陵山区的面积占全国土地资源的69%,但适宜丘陵山区的机具匮乏,严重制约着这些地区农业机械化的发展[1-2]。丘陵山地的坡度多为6°~15°,拖拉机在作业时容易发生侧翻以及耕深不均匀的问题,影响作业效率和农作物的生长。为达到与地形相适应的目的,丘陵山地拖拉机需要具备车身调平及农具横向位姿调整功能。在车身调平方面,国外研究较多,技术水平较高[3-6],但对于农具的横向位姿调整研究明显不足。对于中国耕地现状而言,亟需具有横向位姿可调的山地丘陵拖拉机满足我国农业生产需求。
基于中国农业生产的耕地现状以及中国农机的发展水平,中国制定的十三五重点研究专项,专门设立了丘陵山地拖拉机研究专项,拖拉机后悬挂横向位姿调整技术逐渐被国内学者重视起来,并迅速进展。邹爱民[7]对丘陵山地拖拉机后悬挂结构、后悬挂液压系统及后悬挂电液控制系统的具体应用进行了重点分析,但对于后悬挂姿态调整模式及其控制未做深入研究。周浩等[8]设计了拖拉机悬挂旋耕机自动调平控制系统, 通过试验验证了具有自动调平控制系统的旋耕机,作业后地表横向平整度显著提高, 旋耕效果更加理想, 耕深更加稳定。刘林[9]以GDZ-150 型履带式旋耕拖拉机作为研究平台,研究了基于拖拉机三点悬挂的耕作机具调平系统。浙江师范大学蒋俊等[10]对丘陵山地拖拉机的电控液压悬挂系统的运行机理与控制方法进行了分析,在定负载和变负载2 种典型工况下进行了仿真分析。胡炼等[11]设计了—种农机具自动调平控制系统,采用了卡尔曼滤波算法,通过试验验证了调平控制算法的可靠性,实现了农机具的自动调平控制。
目前,对于拖拉机后悬挂的调平或者姿态调整研究仅限于单侧液压缸调整或者旋耕机的调整,本文主要针对中等马力丘陵山地拖拉机的三点式后悬挂机构横向位姿调整问题设计了—种双液压缸同时调整的液压系统,并采用模糊PID 控制方法,对所设计的横向位姿调整液压系统进行仿真分析,并进行了台架试验。
1 横向位姿调整机构设计
丘陵山地拖拉机作业过程中需要进行后悬挂机构的姿态调节,其目标为在1 s 内实现±15°的横向位姿角度调节,且耕深保持不变。因此,针对丘陵山地拖拉机作业需求,本文设计了—种基于液压缸可变长度提升杆拖拉机后悬挂机构,2 个液压缸活塞杆的相对位移关系决定了农具的倾斜角度以及调整范围,本文首先进行横向位姿调整机构分析。
1.1 基于双液压缸的后悬挂横向位姿调整机构
针对拖拉机三点式悬挂机构,提出基于双液压缸的后悬挂横向位姿调整机构。横向位姿调整方式可以分2 类:第1 类,采用伺服电机驱动的滚珠丝杠构提升杆;第2 类,采用液压缸提升杆。鉴于拖拉机的作业工况,选择液压调整方式。利用液压缸活塞带动下拉杆产生横向角度,采用电液比例阀调节液压缸活塞杆速度。由于机构本身自由度的限制,结合丘陵山地的耕地地形变化,后悬挂提升杆采用2 个双向非对称液压缸,实现在双向15°范围内横向位姿可调,使农机具与倾斜地面保持平行[1-5]。
坡度自适应液压后悬挂机构是为主动全姿态调整丘陵山地拖拉机设计的,采用主动独立姿态调控前驱动装置的控制方式和刚性结构柔性姿态调节的独立悬架后驱动方式,实现整机各种作业工况下的主动全姿态调控。动力输出为双速、后置、非独立式,电液提升器提升力≥8 000 N、额定牵引力≥7 000 N、爬坡度≥20°、后悬挂等高作业坡度≥15°。丘陵山地拖拉机后悬挂横向位姿调整装置组成示意图如图1 所示 。
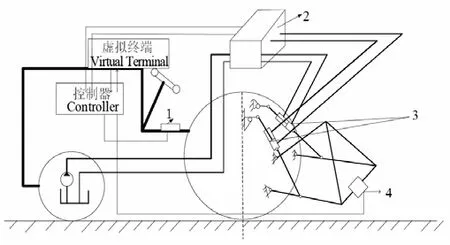
图1 拖拉机后悬挂横向位姿调整装置组成 Fig.1 Composition of lateral pose adjustment device of tractor rear suspension
1.2 横向位姿调整控制策略
丘陵山地拖拉机采用了车身调平机构,遇到横向坡度可以自动调整车身横向角度,调整范围β≤15°。在坡度较小(β≤2°)工况下,后悬挂不需要进行调整,液压缸没有动作。当横向坡度为2°~15°时,后悬挂提升杆双液压缸动作,依据车身倾角与农具倾角的反馈差值进行调整,自动调整流程图如图2。
1.3 横向位姿调整机构运动学分析
为得出液压缸活塞杆位移与农具横向倾角的关系,以进行横向位姿调整机构控制,需进行横向位姿调整机构的运动特性分析。本文将后悬挂下拉杆以及活塞杆简化到—个平面内,建立液压缸活塞杆位移与倾斜角度的几何关系函数(本文以后悬挂三角架角度为倾斜角度,试验中的角度传感器安装位置也位于此)。
自耕深位置最大处开始,令左侧液压缸活塞杆位移变为最小,右侧液压缸活塞杆位移变为最大,使2 个液压缸活塞杆位移的差值从0 逐渐增大至100 mm。悬挂机构横向位姿状态如图3 所示。

图2 拖拉机后悬挂横向位姿调整控制流程图 Fig.2 Control flow chart of lateral pose adjustment of tractor rear suspension
在△ABC’中:
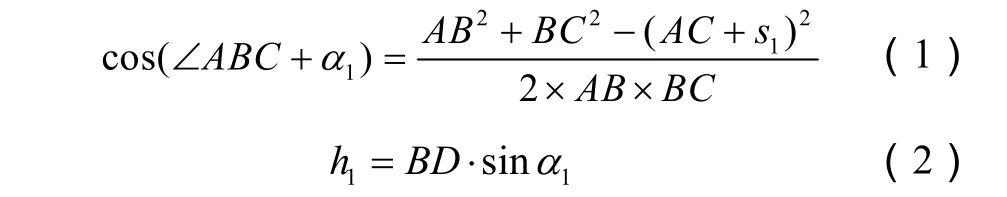
式中α1为左侧液压缸活塞杆与水平面夹角,(°);s1为左侧液压缸活塞杆位移,mm。

式中α2为右侧液压缸活塞杆与水平面夹角,(°);s2为右侧液压缸活塞杆位移,mm。
在△M’GN’中,
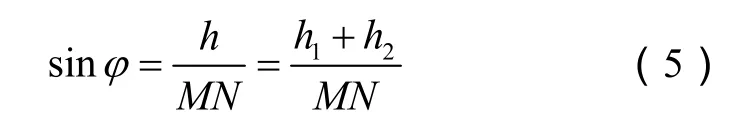
式中h1为左侧下拉杆悬挂点D'到水平面的垂直距离,mm;h2为右侧下拉杆悬挂点D''到水平面的垂直距离,mm;h 为农具左侧悬挂点M'与右侧悬挂点N'的垂直变化距离,mm。
本液压系统中,采用了非对称液压缸,即活塞两端面积不相等,其比例公式如下:

式中s1、s2为液压缸杆位移,m。D、d 为液压缸活塞直径和活塞杆直径,m。以右侧液压缸(AC'')为研究对象,以s2为自变量,建立农具倾角φ 与液压缸活塞杆位移s2的函数,如式(7)~式(8)所示。当s2>0 时,活塞杆做提升运动;当s2<0、液压缸反向运动时,活塞杆做下放运动,当s2=0 时 活塞杆无运动。
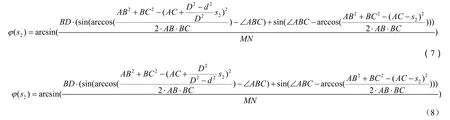
式(7)~式(8)中,∠ABC 为△ABC 内角B 的度数,(°);D 为提升杆液压缸缸筒内径,mm;d 为提升杆液压缸活塞直径,mm;AB 为铰接点A 与铰接点B 之间的长度,mm;BC 为铰接点B 与铰接点C 之间的长度,mm;AC 为左、右两侧提升杆的原始长度,mm; BD 为左、右两侧下拉杆的长度,mm。△h 为农具横梁MN 中点的垂直变化距离,mm。
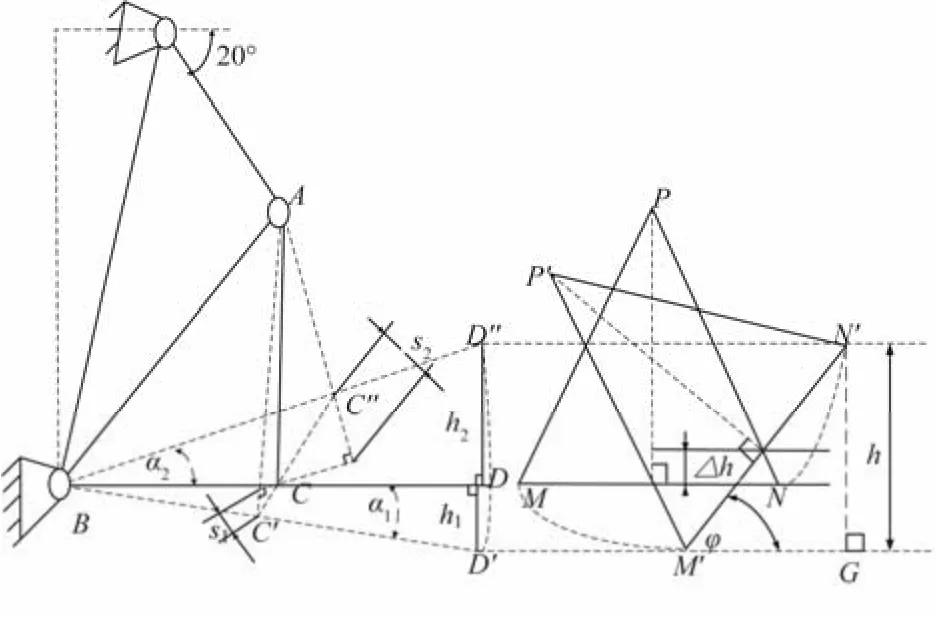
图3 液压缸运动与农具横向平面转角关系 Fig.3 Relationship between movement of hydraulic cylinders and lateral plane angle of agricultural tools
如图3 所示,△ABC 为下拉杆处于水平面时的简化图,将空间机构简化为平面机构便于分析几何关系。△PMN 为悬挂农具的三角架,△P’M’N’为横向调整后三角架位置。图中可以看出,由于为非对称液压缸,液压缸活塞杆位移s1(AC'-AC)与s2(AC- AC'')不相等,导致△PMN 不能围绕中间点旋转。因此,形成了影响耕深的可由后悬挂的提升下降液压缸在原耕深基础上进行修正调节,其几何关系如下:
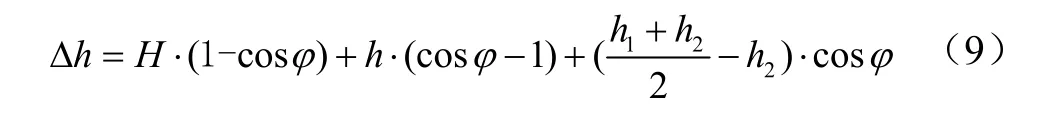
基于式(7)~(8),采用MATLAB 编程进行仿真。根据液压缸活塞杆最大行程,将仿真范围在设定为正负100 mm,仿真得到液压缸活塞杆位移与横向角度的关系,如图4 所示。
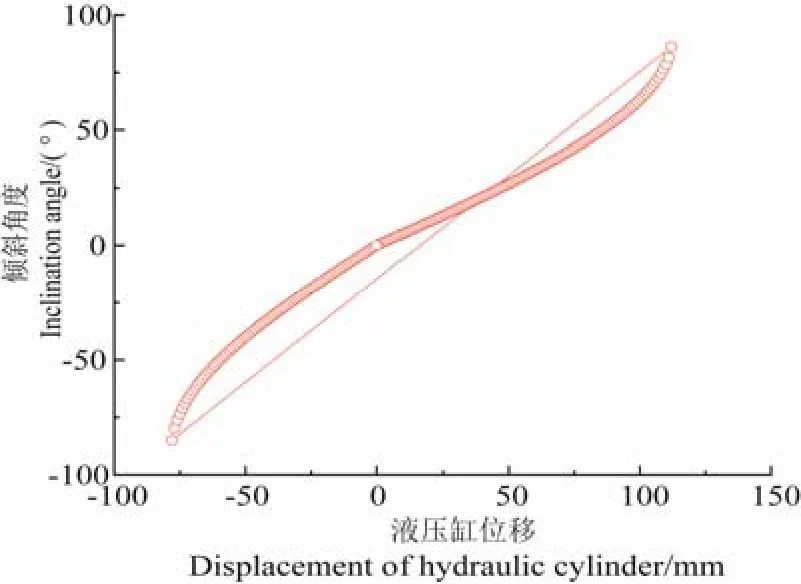
图4 液压缸活塞杆位移与后悬挂倾角的关系 Fig.4 Relationship between displacement of hydraulic cylinder piston rod and rear suspension inclination angle
2 横向位姿调整机构液压系统设计
根据丘陵山地拖拉机后悬挂机构横向位姿调整的设计要求,液压系统采用定量负载敏感回路。该液压系统有2 个活塞式液压缸代替后悬挂提升杆,有自动调整与手动调整2 种模式;同时,在横向位姿调整完成后,后悬挂能够保持与坡地的平行姿态,在液压油路上采用了液压锁;根据图4,在±15° 范围内,后悬挂倾角与液压缸活塞杆位移成线性关系,因此确定后悬挂的调整角度为±15°。后悬双侧液压缸均采用HSG40/22-180×408,液压缸活塞杆最大行程为180 mm,内径32 mm,外径40 mm,活塞杆直径22 mm,公称压力7.4 MPa;由于机构对液压缸行程的约束,液压缸活塞杆单侧最大行程50 mm,双侧行程差100 mm。确定液压系统的主要元器件型号及个数如表1 所示,液压系统的原理如图5 所示。
丘陵山地拖拉机横向位姿调整过程为:在坡度 ≤ 15°的工况下,拖拉机启动自动调平功能。齿轮泵3 在发动机启动后—直工作,液压油经吸油过滤器4、齿轮泵3 到达定差减压阀5,当齿轮泵3 输出油液压力达16 MPa后,油液经溢流阀1 流回油箱。高压油经过定差减压阀5、节流阀10 进入三位五通电液比例换向阀,对应调整角度的方向(左倾15°或者右倾15°)分别启动比例阀,安装在农机具的反馈信号与车身倾角传感器的差值作为控制信号反馈给控制器,形成闭环控制。当差值为零(≤2°),对应的电液比例阀关闭,不再给液压缸供油,液压锁关闭,横向位姿调整结束。同时,本液压系统采用负载敏感设计,通过单向阀6 将最大压力反馈到差压式溢流阀2,如果出现负载突然变大导致压力升高,液压油经差压式溢流阀流回油箱,起到保护液压回路元器件的作用。同时,由于采用液压锁设计,可以将液压缸锁定在某—位置,避免负载传感小流量泄露导致的液压缸振动以及频繁调整。当坡度开始减小、直到车身倾角传感器与农具倾角传感器差值≥2°时,差值信号反馈给模糊PID 控制器,经过控制器处理,电磁换向阀重新接通,右侧液压缸11 和左侧液压缸12 重新调整活塞杆位移,直至达到差值<2°,横向位姿调整结束。

表1 液压系统各液压元件的名称与型号 Table 1 Name and model of each hydraulic component of hydraulic system
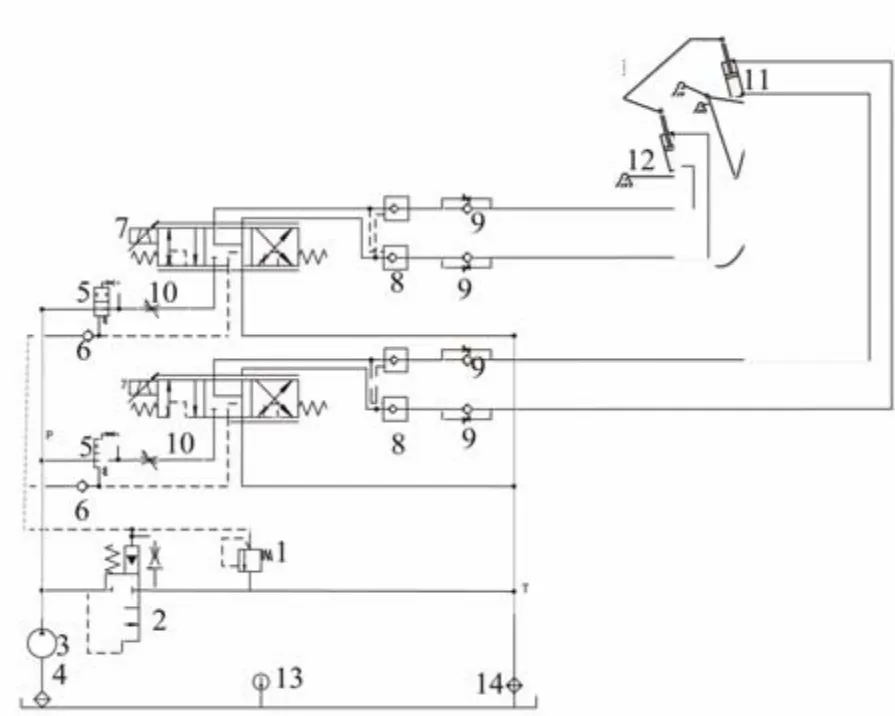
图5 横向位姿调整液压系统原理图 Fig.5 Lateral pose adjustment hydraulic system schematic
3 横向位姿调整机构液压系统建模与分析
3.1 数学模型的建立
在横向位姿调整液压系统中,采用了三位五通电液比例阀以及非对称活塞液压缸,液压原理如图6 所示。因此阀控液压缸的建模主要包括电液比例阀的流量方程、液压缸流量连续性方程和液压缸力平衡方程[12]。数学模型分析如下:
1)力平衡方程
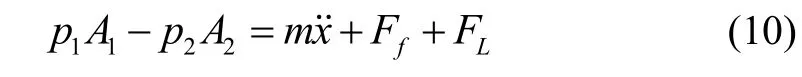
式中m 为活塞与所有连接物体的总质量,1 600 kg;x 为液压缸活塞杆位移,m;p1和p2为液压缸的输入和输出腔体压力,Pa;A1,A2分别是2 个腔体的有效活塞面积,分别为8.038 4e-4和4.898 4e-4m2;FL为外部负载力,包括黏性阻力,N;Ff为活塞上的摩擦力,N。
2)负载流量连续性方程
对于出现泄漏的双向液压缸系统,其流量连续性方程[13-18]为

式中V1=0.000 34,V2=0.000 097,分别为左室和右室的原始控制体积[19-27],包括阀、管道和液压缸控制腔的体积m3;βe为体积弹性模模量,6.85 e8Pa;q1为向左室提供的流量,q2为右室的回流流量,m3/s;qi为内部泄漏流量,qe1和qi2为外部泄露流量,m3/s。
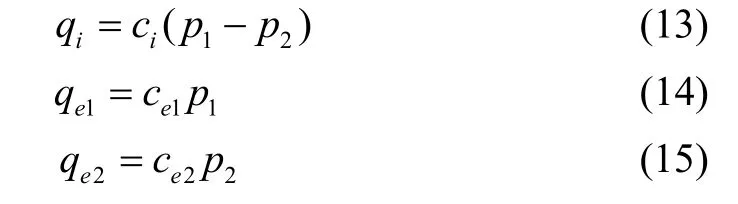
式中 ci=1 097,为内部泄漏系数, m3/(s·MPa);ce1=ce2=120,为外部泄漏系数,m3/(s·MPa);
3) 阀口流量方程:

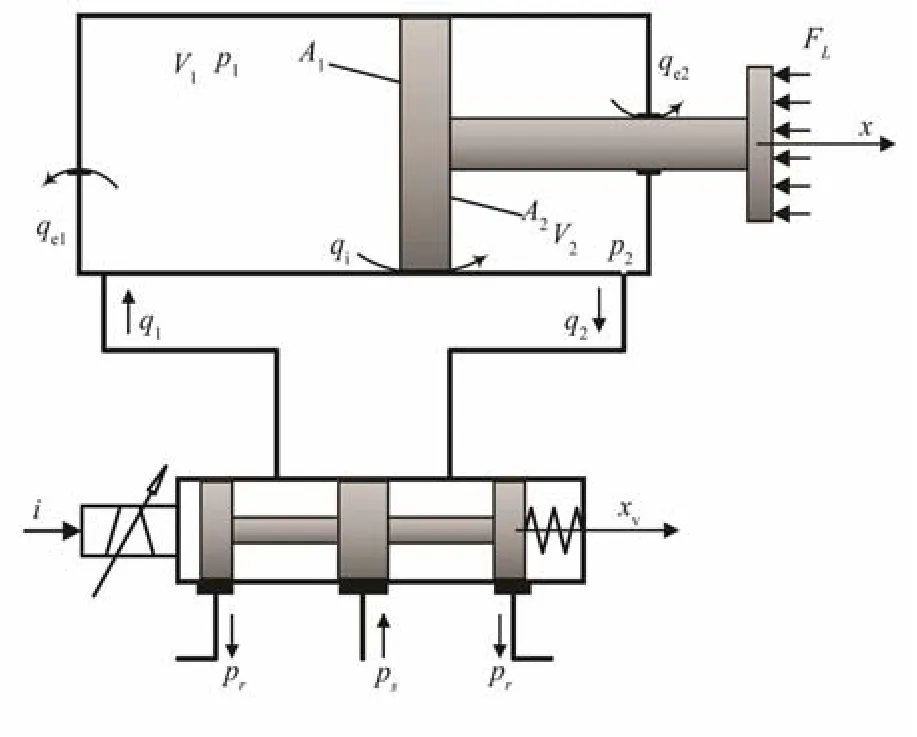
图6 横向位姿调整阀控液压缸原理图 Fig.6 Schematic diagram of lateral pose adjustment valve-controlled hydraulic cylinder
其中 s ( xv)函数[28]的定义如下:

式(16)~(20)中kq1= kq2=2.68×10-5,为流量增益,是关于面积梯度的函数,无量纲;ps为油源压力,Pa;pr为回油压力,Pa;xv为换向阀阀芯位移,m;Cd=0.68,为流量系数,无量纲; w1= w2=0.023 7,为阀芯节流口面积梯度,m;ρ=850,为液压油密度,kg/m3。
将上述公式整理可得:
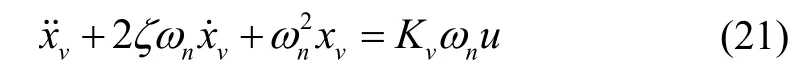
式中ζ =0.5,为阀的阻尼比,无量纲;nω 为阀的固有频率,120.5 rad/s;Kv为阀的电压增益,10.5×10-5m/V;u为输入电压信号,V。

此处

3.2 控制系统建模
依据丘陵山地拖拉机后悬挂横向位姿调整液压原理图,系统采用角度负反馈方式,阀控液压缸模型采用状态反馈方式搭建,采用模糊自适应整定 PID 控制原理,在Simulink 中建立仿真模型。将 PID 控制的规则和条件用模糊集合表示,并将这些模糊规则预先编制好存储在控制器中。根据控制系统的实际运行状况,控制器可以利用模糊推理自适应地调整 PID 参数,从而达到最佳的控制效果。
模糊自适应 PID 控制由 PID 控制器和模糊控制器2 部分组成。模糊控制器以偏差 e 和偏差变化率 ec 为输入,利用事先储存的模糊规则表在线对 PID 参数进行实时调整,得到最合适的参数值,然后将调整好的参数值增量叠加到原本的 PID 控制器中
3.2.1 输入输出变量及其模糊子集的确定
在横向位姿坡度自适应控制中,输入车身倾斜角偏差值以及偏差变化率,输出为PID 控制器的3 个参数修正值Δkp、Δki、Δkd。对模糊控制器而言,控制模式均为双输入三输出的形式。
模糊控制器无法识别连续变量,因此首先要将变量在其论域范围内进行离散化,各变量论域值范围均为[-15,15]。依据确定论域值的划分规则,各变量的离散论域划分[29]如下:
比例系数变化量Δkp 的离散论域为{-15,-10,-2,0, 2,10,15};
积分系数变化量Δki 的离散论域为{-15,-10,-2,0,2, 10,15};
微分系数变化量Δkd 的离散论域为{-15,-10,-2,0,2, 10,15};
各变量的量化等级均为 7 级,相应的模糊子集为{NB,NM,NS,Z,PS,PM,PB},各模糊变量代表的含义分别为“负大”、“负中、“负小”、“零”、“正小”、“正中”、“正大”。
3.2.2 隶属度函数的确定
模糊控制中隶属度函数的形状对控制效果影响较大。隶属度函数形状较尖的模糊子集分辨率高,控制更灵敏。隶属函数较平缓的模糊子集,分辨率低,控制更稳定[29]。各变量的隶属度函数中,当误差为 NB 与 PB 时,为了提高稳定性,NB 采用 zmf 型隶属度函数,PB 采用 smf 型隶属度函数。其他模糊子集均采用 trimf 型隶属度函数,以提高系统的响应速度。
3.2.3 模糊规则的建立
模糊 PID 控制器的模糊规则用来表述输入变量 e、ec 与输出变量Δkp、Δki、Δkd 间的对应关系,如表3 所示。

表3 Δkp、Δki、Δkd 控制规则表 Table 3 Δkp、Δki、Δkd fuzzy control rule table
3.2.4 PID 自适应校正
Δkp、Δki、Δkd的模糊控制规则表建立之后,将系统的输入变量 e、ec的变化范围定义为模糊集上的论域。

设e、ec 和kp、ki、kd 均服从正态分布,因此可以得出各个模糊子集的隶属度,根据模糊子集的隶属度赋值表和各参数模糊控制模型,应用模糊合成推理设计PID参数的模糊矩阵表,查出修正参数代入下式:

运行控制系统过程中,系统通过模糊规则的结果处理、查表、运算,完成对PID 参数的自动校正,如图7 所示。
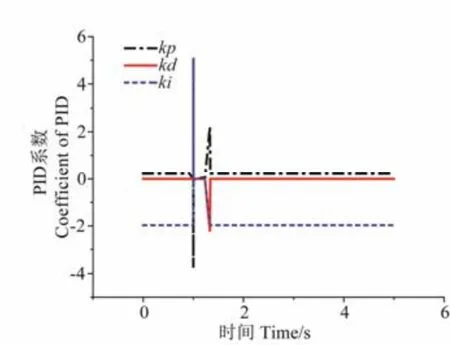
图7 kp、ki、kd 的自适应调整 Fig.7 Adaptive adjustment on coefficients of kp、ki、kd
3.3 仿真结果及其分析
根据采用的液压阀内部结构参数以及液压缸尺寸参数,搭建上述仿真模型,在仿真模型中,用阶跃函数代替实际试验中车身倾角的测量值。由于中国丘陵山地坡度多为10°~15°,分别设定输入值为+10°和+15°,仿真时间为5 s,换向阀控制电压为2.5 V,采用PID 反馈控制2 个液压缸同时移动,将两侧液压缸活塞杆位移绝对值之和作为角度换算的输入值输入到拟合函数,阶跃时间在第2 s,得到2 个液压缸活塞杆位移随时间变化曲线,如图8 所示。

图8 两个液压缸活塞杆位移随时间变化曲线 Fig.8 Displacement versus time curve of two hydraulic cylinders piston rod
由 于液压缸采用非对称活塞杆液压缸,在采用2 个液压缸调节角度时,2 个液压缸活塞杆速度不—样,因此液压缸杆活塞位移在图10 中不对称,2 个液压缸的活塞杆位移绝对值之和等于角度调节所需的单杆液压缸活塞杆调节长度,但速度较单杆液压缸快。
4 验证试验
4.1 试验平台
在中国农业大学上庄试验站,采用五征40 马力拖拉机搭建试验平台,测试后悬挂横向位姿调整角度能否达到设定目标值(10°~15°)。首先,对后悬挂倾角传感器进行了标定,其次,采用手动调节车身倾角传感器作为输入信号。由于采用非对称活塞杆液压缸,启动横向位姿调整前,提升杆两侧液压缸活塞杆伸出量需调整至50 mm,如果采用单侧液压缸角度调整无需预先伸出液压杆,试验采用双液压缸调节和模糊自适应整定PID 控制策略。
拖拉机后悬挂系统控制试验平台主要由液压系统、虚拟终端和数据获取系统3 部分组成,如图9 所示,其中悬挂系统主要由拖拉机液压泵、多路换向阀、升降液压缸、提升杆伸缩液压缸、农具、提升臂及油管等组成;虚拟终端主要由显示器、控制器、倾角传感器、及可变电源等组成;数据获取系统由USBCAN 接口卡和PC 机组成。
拖拉机液压泵额定流量为20 L/min,额定压力为 16 MPa。农具横向倾角传感器由24 V 电源供电,倾角信号输出端与控制器AI21 电流采集端口连接,接地线与控制器AGND 模拟地端口连接,构成回路使控制器采集倾角信号。

图9 实车试验 Fig.9 Real vehicle test
4.2 结果与分析
本试验目的为:设置车身倾角,测试后悬挂经过控制器的输出信号控制液压缸活塞杆位移导致的角度变化是否与仿真结果—致。试验过程中,通过调整车身产生不同的倾斜角度,控制器输出控制电流,使两侧液压缸活塞产生位移,达到调节农具横向倾角的目的,调整效果如图9 所示。
保存数据并处理,得到农具横向倾角随时间变化的曲线,如图10 所示,在前2 s 内显示器—共发送10 次增加电磁铁输入电流的控制信号,每次使得控制两侧液压缸活塞杆提升的PWM3 占空比增加5%,最终PWM3 的占空比为50%,两侧液压缸活塞杆运动时间约1 s,农具横向倾角由0°上升为10°。
本试验中,换向阀开启的死区电压4.2 V,PWM3 占空比≤35%时,阀芯不能开启。

图10 倾角变化曲线 Fig.10 Inclination change curve
在试验数据采集中,由于后悬挂结构的不稳定性以及测量误差等原因,三点悬挂铰接部件产生干涉,试验采集数据在初始阶段振荡严重,导致试验和仿真数据误差较大。车身调平的同时,采用PID 控制器根据车身倾角传感器对后悬挂进行横向位姿调整,由图10 可知,稳定后的仿真数据和试验采集数最大误差为1%,平均误差为0.7%;仿真试验中模糊 PID 自适应控制的过渡过程时间不足0.2 s,系统无超调。实际试验的调整时间为1 s左右,试验调量为0,目标值与试验数据的最大误差13.3%,平均误差10%。
5 结 论
本文针对于丘陵山地拖拉机设计了三点式后悬挂的横向位姿调整液压和控制系统,并进行了仿真试验与台架试验,主要结论如下:
1) 通过MATLAB 软件对系统进行运动学仿真,得出100 mm 液压缸活塞杆行程内,后悬挂机构倾斜角度与液压缸活塞杆位移的函数关系,并将其应用到仿真控制模型中。
2) 根据丘陵山地拖拉机电液悬挂控制系统的特点进行液压回路的分析,搭建了双液压缸横向位姿调节液压系统模糊PID 仿真控制模型并进行了台架试验。设定倾斜角度由0°阶跃至15°时,系统过渡过程时间为 1 s,系统超调量为 0,系统控制平稳。结果表明,本文所设计的后悬挂机构能适应地形的在±15°范围内的变化,满足拖拉机在山地丘陵作业过程中的横向位姿调节需求。

