基于改进粒子群算法的大迟延热工对象PID参数优化

马鑫泰，何同祥

（华北电力大学 控制与计算机工程学院，河北 保定 071003）

0 引言

PID控制器具有原理简单、使用方便、适应性强、鲁棒性强等特点，在工程中被广泛应用[1]。尽管PID控制器具有很多优点，但是应用于热工对象的PID控制器参数整定具有一定难度，尤其对于具有大惯性、大迟延的热工对象，采用常规整定方法如Z-N、C-C、ITAE阶跃响应曲线法以及衰减曲线法等工程整定方法，来整定PID参数变得较为困难，不易于获得良好的控制效果。随着智能优化算法的普及，控制器参数的整定方法越来越多。粒子群算法具有原理简单、易于实现的特点，其发展较为迅速[2]。本文对粒子群算法进行改进，利用改进的算法对PID参数进行整定优化，并应用于大迟延热工对象，取得良好的控制效果。

1 粒子群算法（PSO）的改进

1.1 粒子群算法原理

粒子群算法[2,3]（Particle Swarm Optimization，PSO）最早由Kennedy和Eberhart于1995年提出来的，是一种群智能优化算法。粒子群算法是针对鸟类捕食这一行为，进而产生的一个模型。

粒子群算法的核心是将优化问题的解看作空间中的一个粒子，空间的维度是由优化问题解的个数决定的。例如PID参数的优化，有3个参数，即在一个三维空间中去寻找一个最优解。空间中每个粒子的飞行方向及飞行长度都会被目标函数所约束，在此过程中会产生两个最优值，个体最优值Xbest和种群最优值XBEST。

确定目标问题解的个数N以及种群中的粒子规模M，即在N维空间中的M组可能解中寻找一组最优解。其中，第i个粒子的位置可以表示成Xi=(xi1,xi2,…,xiN)，i=1,2,…,M；速度可以表示成Vi=(vi1,vi2,…,viN)，i=1,2,…,M。将位置坐标Xi带入到所设定的目标函数Q(x)中，计算出各个粒子的适应度，根据适应度的大小进而判断粒子位置Xi的好坏。经过一段时间的寻优，产生个体最优位置Xbest=(xi1,xi2,…,xiN)以及种群最优位置XBEST=(xg1,xg2,…,xgN)，每个粒子根据式（1）和式（2）来更新自己的速度和位置，如下：

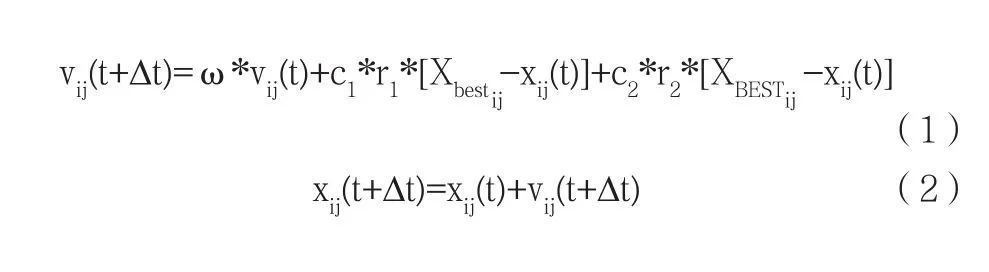
式（1）中，ω为权重系数，c1与c2分别为个体学习因子和种群学习因子，r1和r2为0～1之间的随机数。随着寻优的进行，权重系数会根据式（3）得到线性更新，如下：

式（3）中，ωmax和ωmin分别为ω的最大值和最小值，k为当前走过的步数，Zmax为最大寻优步数。

如此迭代下去，直到取得最优值。

1.2 粒子群算法改进

本文从两个方面对粒子群算法进行改进：第一，对粒子群算法的个体学习因子及种群学习因子进行改进；第二，利用PID控制器经验整定公式对粒子群参数寻优区间进行改进。

个体学习因子c1为个体寻找自身最优位置的权重系数，种群学习因子c2为个体靠近种群最优位置的权重系数。引入α系数使个体学习因子和种群学习因子进行非线性变化，系数α由式（4）进行表示，如下：

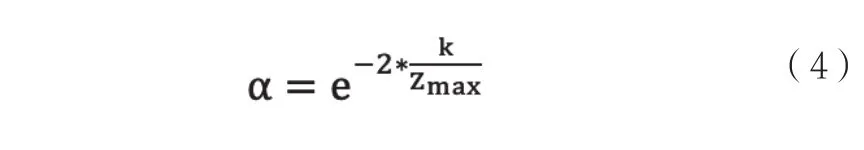
式（4）中，k为当前走过的步数，Zmax为最大寻优步数。

将个体学习因子c1和种群学习因子c2进行如式（5）和式（6）改进，即：

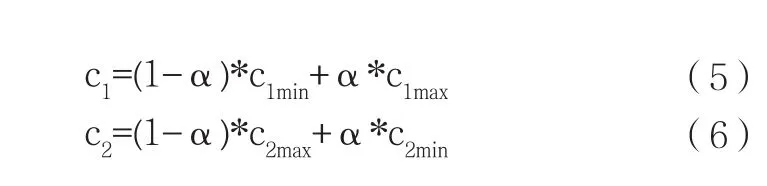
式中，c1max和c1min分别为c1的最大值和最小值，c2max和c2min分别为c2的最大值和最小值。

改进前的个体学习因子和种群学习因子一般取定值2，寻优的过程中，学习因子一直不变。因此，其寻优过程中可能会错过最优值。改进后，个体学习因子和种群学习因子随着寻优进行非线性变化，对于寻找最优位置更具有针对性。寻优的前期，使个体学习因子取值较大，自身去寻找个体的最优位置，使之完善自身位置，达到理想的位置；寻优的后期，使种群学习因子增大，利用种群去寻找最优位置，直至取得最优值。改进粒子群算法有效地避免了粒子群算法已陷入局部最优值的状态，在兼顾搜索精度的基础上，提高了搜索速度。

确定一个合适的参数搜索区间可有效地提高粒子群算法的搜索速度，因而可通过计算来对粒子群算法所优化的参数上下限进行基本确定。根据文献[4]中的经验整定公式，对比例带δ、积分时间常数Ti以及微分时间常数Td3个参数进行计算，确定基本参数δ0、Ti0以及Td0。确定的参数寻优参数范围如下：

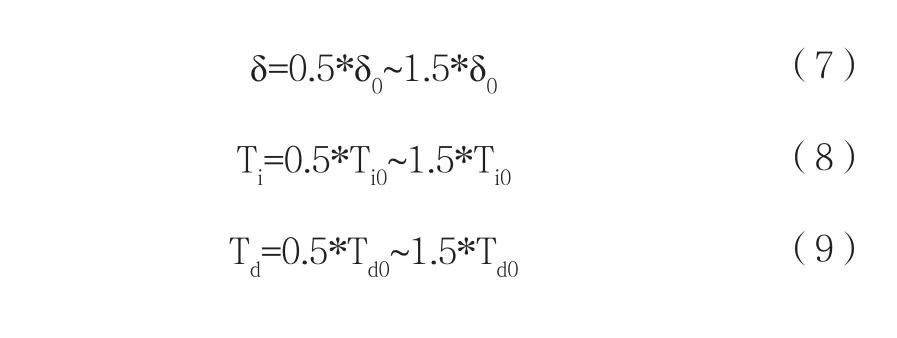
本文对PID控制器参数进行整定优化，它的传递函数为：

式中，δ为比例带，Ti为积分时间常数，Td为微分时间常数。

PID控制器[5]的控制量是由偏差的比例作用（P）、积分作用（I）、微分作用（D），经过线性组合得到的。只有将比例带δ、积分时间常数Ti以及微分时间常数Td三者的组合最优时，控制器才会产生良好的控制效果，进而达到稳、准、快的效果。

1.3 目标函数的设计

整定PID控制器参数的过程是以目标函数为核心的，即想要达到的控制效果可由目标函数进行限制。为了得到良好的动态特性同时避免过大的控制量，将误差绝对值的时间积分性能指标（ITAE）和控制器输出的平方项加入到目标函数中。同时给二者用权重系数b1和b2进行限制。目标函数如下：

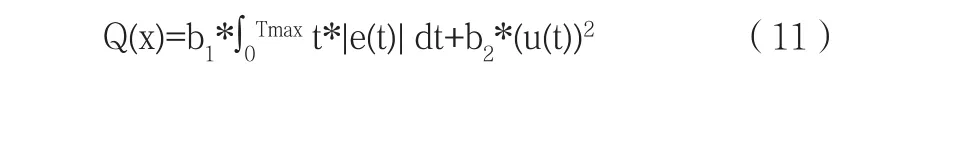
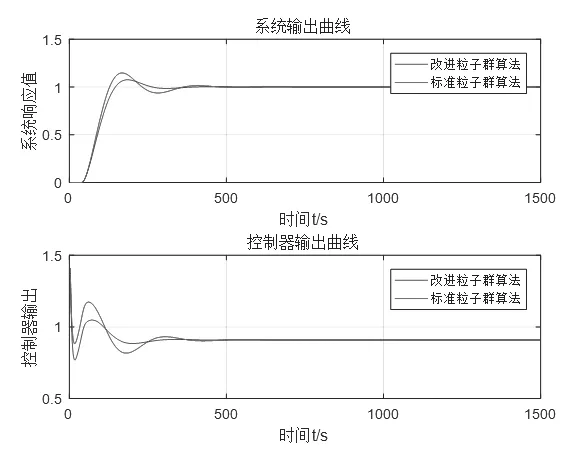
图1 两种方法对比仿真曲线Fig.1 Comparison of two methods to simulate the curve

2 改进的算法应用于大迟延热工对象的PID参数整定

为了检验改进粒子群算法整定出的PID参数应用于大迟延热工对象上的效果，对一个热工对象进行仿真及研究。

选取的热工对象的传递函数为：

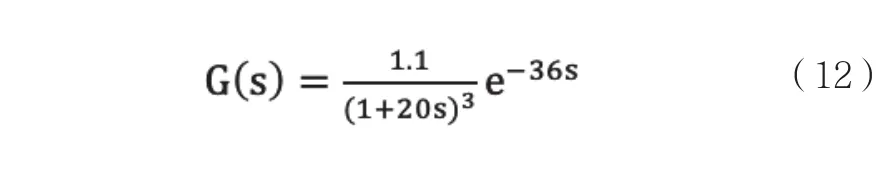
利用经验公式整定出的基本参数：δ=1.6929，Ti=57.6，Td=7.2～14.4。

寻优参数的范围：δ=0.8～2.6，Ti=28～87，Td=3.5～22。

改进粒子群算法寻优设定值：定值扰动信号为单位阶跃信号，优化PID参数的个数为3，粒子的总数为100，惯性系数的上下限为ω=0.4～1.6，个体学习因子的上下限为c1=0.5～2.5，种群学习因子的上下限为c2=0.5～2.5，比例带参数寻优的速度上下限为v1=-0.2～0.2，积分时间常数参数寻优的速度上下限为v2=-2～2，微分时间常数参数寻优的速度上下限为v3=-1～1。

寻优结果：δ=1.8652，Ti=52.3806,Td=10.8253。

仿真曲线如图1所示。

由曲线可知：与标准粒子群算法整定出的PID参数相比，改进的粒子群算法整定出的PID控制器参数，具有良好的控制效果，减小了超调量同时减小控制器输出的波动。因此，改进粒子群算法是合理可行的。

3 结语

本文在粒子群算法的基础上，提出了改进粒子群算法，并将改进的算法应用到大迟延热工对象的PID控制器参数整定中，得到了良好的控制效果。通过MATLAB仿真验证了改进粒子群算法的优越性，针对大迟延热工对象，该算法可有效克制被控对象的大迟延，在兼顾系统的快速性的基础上，抑制了系统的超调量，从而提高了控制效果。