海外项目平面控制测量起算数据获取方法研究与可靠性验证

朱延坡

(中铁工程设计咨询集团有限公司郑州设计院，河南郑州 450001)

在利用GPS相对定位方法建立平面控制网时，常规做法是联测高等级的起算点，得到起算点所在坐标系下的控制成果，该方法既能满足精度要求，又可以实现与当地政府规划坐标保持一致[15]。然而，部分国家或地区缺少必要的起算数据，国内专家对此也进行了诸多研究。例如刘文斌等[14]采用GPS测量的方法，虽然相对精度满足要求，但是绝对坐标难以实现与当地规划坐标的衔接；贾登科等[2]在欠发达国家采用联测IGS参考站的方法，虽然获得了满足规范要求的绝对坐标，但未考虑WGS84精化对测量成果的影响。以下基于既有的理论基础，探讨较为严谨的平面控制网起算数据获取办法。

IGS组织由超过400个持续运行的GNSS参考站、4个IGS全球数据中心和多个区域数据中心组成。用户通过专业网站可以下载全球GNSS系统的精密星历、IGS参考站坐标和速度场等[10]。IGS参考站采用ITRF框架坐标，具有毫米级精度。因此，通过联测IGS参考站，理论上可以为项目提供满足精度要求的起算点数据。联测IGS站的基线长通常为数百公里，而一般的商用解算软件只能解算几十公里的基线，故采用解算能力较强的GAMIT软件进行基线解算。

工作原理为:按照控制网分级布设原则，首先获得起算点的坐标成果。以长基线解算软件GAMIT为基础，对起算点野外观测数据和IGS参考站观测数据进行联合解算，得到合格的基线解算成果。以IGS参考站框架坐标为已知点进行约束平差，通过历元转换和坐标转换，获得本项目的起算数据。考虑到IGS站的空间分布[12]、基线解算及数学换算对计算结果的影响，采用两种不同的方法建立测区控制网:以该起算数据为已知点，经约束平差得到项目的首级控制网成果；以二维联合平差法对首级控制网进行约束，得到该方法下的控制网成果；采用两套控制点成果反算边长并进行对比，验证该方法的可靠性。

1 起算数据获取

1.1 项目概述

安科罗-马诺诺道路修复和现代化项目位于刚果(金)加丹加省(Katanga)马诺诺(Manono)地区。项目起点为马诺诺市，沿西北方向经 KOKOLE、DLANDALA、KITAMATA、MUSWELO、SEYERINO，终至MUYUMBA，长约41.5 km，设计车速60 km/h。道路沿线没有任何平面控制点。

1.2 坐标系统参数

按照规范规定，本项目首级控制网采用一级平面控制测量，起算点测量等级不低于四等，采用WGS84参考椭球、高斯投影。为了保证投影变形不大于25 mm/km，并兼顾后期施工方便及与当地成果的衔接，提供了两套不同的投影成果(UTM投影成果用于与当地政府规划衔接；高斯投影成果用于工程测量)。为了保证坐标值均为正值，东坐标和北坐标的加常数分别为500 km和10 000 km。

1.3 数据采集及处理

(1)标石埋设

按照规范要求，在马诺诺-安科罗道路沿线地表基础稳定、点位易于保存处，每隔4 km左右布设单点或点对，全线共布设17个控制点(见图1)。其中，GPS1～GPS6位于马诺诺市周边；线路起终点为GPS4和GP17(间距约为40 km)。

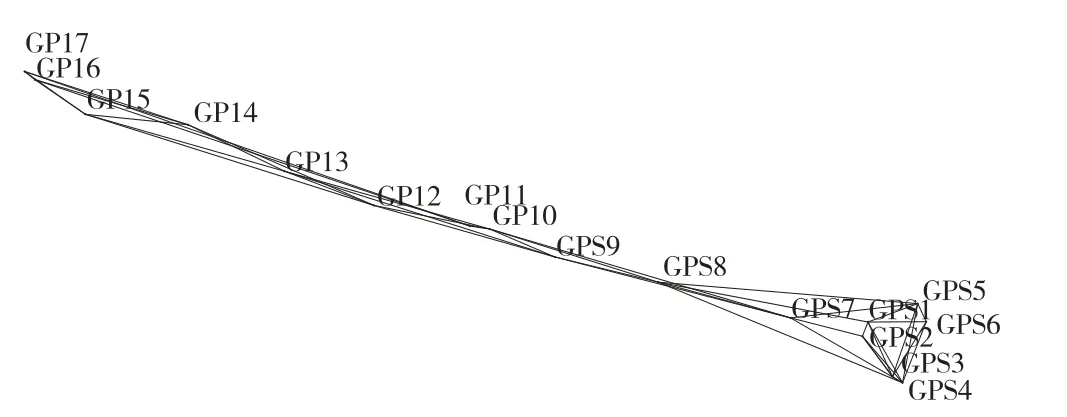
图1 控制点平面位置示意

(2)数据采集

本项目采用的南方S82双频接收机，经测量仪器检定机构检定为合格，且在其检验的有效期限内。在起算点GPS4和GP17上分别架设GPS接收机，以同步观测方式观测2个时段(每时段不少于6 h)[9]；数据采样间隔与IGS观测数据保持一致，均为30 s，截止高度角为10°。天线高在每个观测时段观测前后各量取一次，两次量高之差在误差范围内时，取两次的平均值为最后的天线高[3]。在第一个观测时段结束后，重新对中整平，方可开始第二时段测量。

(3)下载IGS参考站坐标数据

根据野外观测时间，下载计算所需的数据，主要包括对应年积日的rinex格式观测数据、导航文件和sp3格式的事后精密星历；根据测区位置选择周边合适的IGS参考站点，依据精密星历中所采用的ITRF参考框架(本项目为ITRF2008框架)和外业观测对应的年积日，下载相对应的空间坐标，见图2。

图2 IGS参考站站点ITRF08坐标

(4)基线解算

①将野外观测数据转换成标准rinex格式，和IGS参考站观测数据一起放入GAMIT软件项目目录mnn的rinex文件夹中；精密星历和广播星历分别放入igs文件夹和brdc文件夹下。②运行“sh_setup-yr 2016”，更新tables文件。③设置sites.defaults文件中参与运算的IGS站点、station.info文件更新、sestbl.中的全球海洋潮模型、process.defaults中的采样间隔、观测历元数及开始结束时间等文件。④采用批处理，运行sh_gamit-d 2016 166，对观测数据和IGS站数据进行基线解算；两个时段分开解算，分别获得两个观测时段基线解算成果的qexpta文件。⑤将qexpta文件写入“cosagps for gamit q-file”，并拷贝至windows系统下待用。

nrms作为判断基线解算质量的重要指标之一，通常小于0.3视为该质量评定指标合格。如果nrms超过0.5，应对数据进行检查，并重新处理基线[11]。本例中，两个时段nrms=0.23(满足要求)，解算结果见图3。

图3 GAMIT基线解算nrms结果

(5)网平差

结合qexpta文件，运用CosaGPS软件，以点NKLG三维框架坐标作为已知点，进行三维无约束平差，重复基线测量的差值≤2 2σ，GPS网同步环分量闭合差≤，异步环各坐标分量闭合差≤3 nσ，独立异步环坐标闭合差≤3 nσ，基线分量的改正数绝对值≤3σ，均满足规范要求。

以三个IGS站为已知点，进行三维约束平差，基线分量的改正数与同一基线无约束平差改正数较差的绝对值≤2σ，满足规范要求，GPS4和GP17的空间直角坐标见表1。

表1 起算点ITRF08框架2 016.454历元空间直角坐标

(6)历元换算

上述计算得到的GPS4和GP17空间直角坐标是观测历元时的坐标，需对上述成果进行统一框架下的历元换算，得到与WGS84(G1674)对应的框架坐标，即将2 016.454历元的坐标换算到统一框架下的2 005.0历元坐标。由于地壳运动，IGS测站框架坐标随着历元的改变而变化，因其变化速度缓慢，其运动轨迹可视为匀速线性[8]。因此，统一框架下的历元换算可表示为

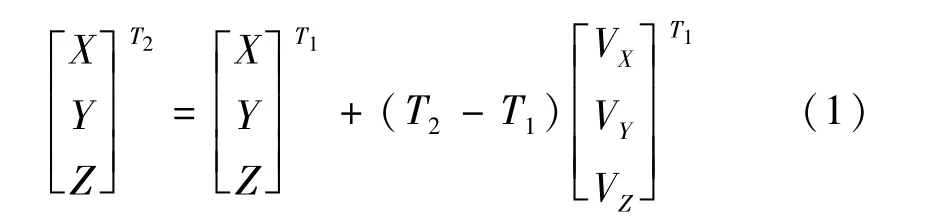
(7)坐标转换和高斯正算

①同一参考椭球下空间直角坐标与大地坐标的变换[4]

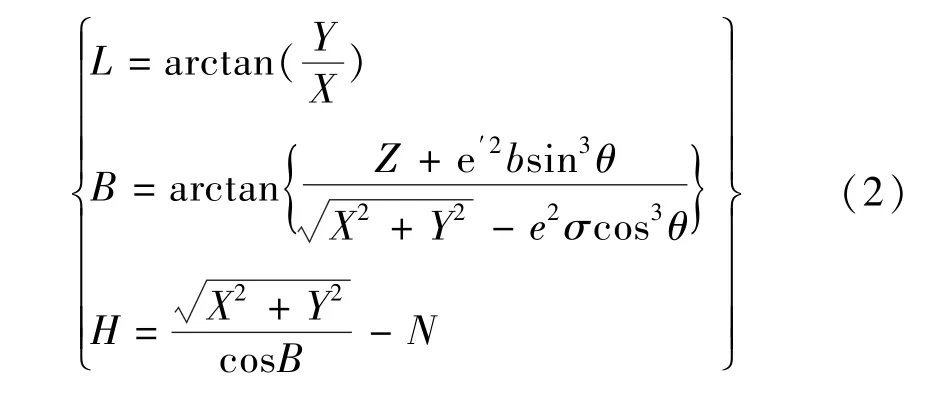
式中，e′为参考椭球的第二偏心率；

由公式(2)和公式(4)，得到GPS4和GP17在WGS84参考椭球下的高斯投影3°带第9带的平面直角坐标，作为本项目首级平面控制网的起算数据。GPS4和GP17的高斯平面直角坐标见表2。

表2 起算点高斯平面坐标 m

2 可靠性验证

首级控制网野外观测结束后，采用两种方法进行约束平差，即以表2中的起算点进行约束平差和联合/约束平差，通过两种不同方法的成果对比，验证联测IGS参考站获取起算点方法的可靠性。

首级控制网测量等级为一级，采用4台双频南方S82接收机进行观测。采用边连式布网，相对定位作业模式。观测时段长按照规范规定执行，高度截止角为15°，起算点GPS4和GP17与首级控制网同步观测。

将观测数据转换成标准rinex格式，分别用徕卡LGO软件进行基线解算、CosaGPS软件进行网约束平差。无约束平差时，起算依据采用GP17三维坐标。同一基线测量的差值≤2 2σ，GPS网同步环分量闭合差异步环各坐标分量闭合差≤3 nσ，独立异步环坐标闭合差≤3 nσ，基线分量的改正数绝对值≤3σ，均满足规范要求。

2.1 平差方法一

以GPS4和GP17为起算点，进行二维约束平差，计算出其他GPS点的平面坐标成果。

最弱点点位相对中误差为0.34 cm，小于规范要求(±5 cm)；最弱相邻点边长相对中误差为1/222 000，小于四等控制测量的规范要求(1/35 000)。

按照规范，测区内投影变形应在一定范围内[5]，计算公式为

式中，Δs1为实测边长归算到参考椭球面上的变形影响值，Δs2为参考椭球面上的边长归算到高斯投影面上的变形影响值，Δs为测区内的投影变形值，Hm为归算边高出参考椭球面的平均高程，s为归算边的长度，R为归算边方向参考椭球法截弧的曲率半径。即s0为投影归算边长，ym为归算边两端点横坐标平均值，Rm为参考椭球面平均曲率半径。

为了保证Δs满足规范要求，可采用以下方式:选择合适的高程参考面的抵偿投影面、移动中央子午线的任意带高斯正形投影，同时改变高程参考面和中央子午线高程抵偿面的任意带高斯投影。本测区在27°02′～27°24′之间，离中央子线(27°)的最大距离为42 km左右，投影变形主要来自于Δs1的影响。因此，本项目采用抵偿投影面的高斯投影，即选择合适的高程投影面，以保证投影边长长度满足规范要求。

令Δs=Δs1+Δs2=0，当ym一定时，有

根据上述公式，求得ΔH=49 m

则投影面高为

取高程投影面为550 m，将所有控制点成果转换到该投影面上，得到该方法下的最终控制网成果。

2.2 平差方法二

在控制网无约束平差后，只输入一个已知点的坐标，再输入一条地面边长(经过温度、气压和大气折光改正，不进行高程归化和高斯投影变形改化)和该边的自带方位角，将地面边长和地面方位角作为固定值进行约束平差，得到控制网的平面成果。以GP17的平面坐标、GP16～GP17的实际观测距离及GP16～GP17方位角为固定值，用CosaGPS软件进行约束平差，其最弱点点位相对中误差和最弱相邻点边长相对中误差均满足公路四等测量规范要求。

2.3 对比论证

方法一获得的控制点成果的绝对坐标可以达到厘米级精度[2]，将方法一的控制点反算边长与方法二的控制点反算边长进行对比，见表3。

表3 两种约束方法的控制点成果反算边长对比

从表3可以看出，由联测IGS站获取起算数据的方法完全满足规范精度要求，可以在工程实践中推广运用。

3 结论

⑴可通过联测IGS参考站的方法获取平面控制测量的起算数据。为了兼顾控制网精度、后期施工方便及与当地规划坐标系统的衔接，可以采用两种坐标系统的控制成果，但是需要计算不同坐标系之间的转换参数。

②建议采用专业的长基线解算软件(如GAMIT等)，以保证基线计算的精度；进行二维约束平差时，可以用地面观测边长和方位角等已知数据进行联合约束平差，对控制网成果进行检核。