气控环形防喷器密封胶芯大变形分析*
(1.中国石油大学(华东) 机电工程学院 山东青岛 266580;2.中联煤层气有限责任公司 北京 100011)
在煤层气带压修井中,多采用液控环形防喷器进行井口密封,它密封压力高,适合井内压力高的常规油气井[1]。许多学者从液控环形防喷器的组合方式、液压结构等各方面进行了改进与优化,使其得到了较为广泛的推广与应用[2-4]。由于液控环形防喷器密封压力高,结构复杂,通过油管接箍困难,使修井时间过长;同时由于煤储层产水,修井过程中动液面不断升高,造成“事实压井”,且由于煤本身的脆性、水敏感性和易碎性,在带压修井过程中极易造成储层破坏,影响产能[5-6]。因此,研究人员设计出了密封压力低、油管接箍通过性好、作业效率高的适用于煤层气井的气控环形防喷器。
胶芯是实现防喷器密封的核心,许多学者利用有限元仿真分析的方法对胶芯变形进行了大量的研究。张宝生等[7]研究了锥型胶芯在大变形状态下应力、应变及接触应力的变化规律;贾光政等[8]针对带压作业,利用有限元方法对组合胶芯进行了非线性计算;余长柏等[9]针对胶芯的常见失效形式,对胶芯进行接触动力学分析。同时,许多学者也从结构、材料以及现场使用等方面对防喷器胶芯的失效形式进行研究[10-11],但对于胶芯变形的理论分析较少,而胶芯变形的理论分析对于防喷器的应用和密封性评价有着重要的意义。
本文作者通过分析胶芯材料非线性、几何非线性,结合橡胶本构方程和厚壁筒理论,采用载荷迭代的方法,推导了胶芯无变形阶段、自由变形阶段和接触变形阶段的变形和接触压力方程,并将理论计算结果与仿真结果对比分析,为该类适用于煤层气带压修井防喷器的应用判断和密封性评价提供了理论依据。
1 气控环形防喷器结构与原理
由于煤层气井“排水-降压-解吸-采气”的排采方式和煤层气储层的“低压、低渗透率、低饱和度”的三低特性[12],液控环形防喷器在煤层气带压修井作业中存在密封压力高、胶芯退让性差、过油管接箍困难以及泄压时间长的问题,而气控环形防喷器则可以解决这些问题,可用于煤层气带压修井作业。
1.1 气控环形防喷器结构
气控环形防喷器主要由压盖、壳体、胶芯、气囊、密封圈等组成,其结构如图1所示。自密封壳体和上壳体通过花键连接,胶芯下骨架与下壳体也同样采用花键连接,自密封橡胶起辅助密封作用。在安装胶芯时,先用顶丝实现胶芯与自密封壳体的固定连接,之后,把胶芯连同自密封壳体插入壳体内,并旋转自密封壳体到定位销孔对齐,利用销轴固定。此时,密封壳体与上壳体、胶芯下骨架与下壳体都通过花键啮合的方式实现了固定。为了保证安全,同时利用螺栓连接各个壳体。用花键连接的方式替代螺栓连接,保证了胶芯在磨损后的快速更换。
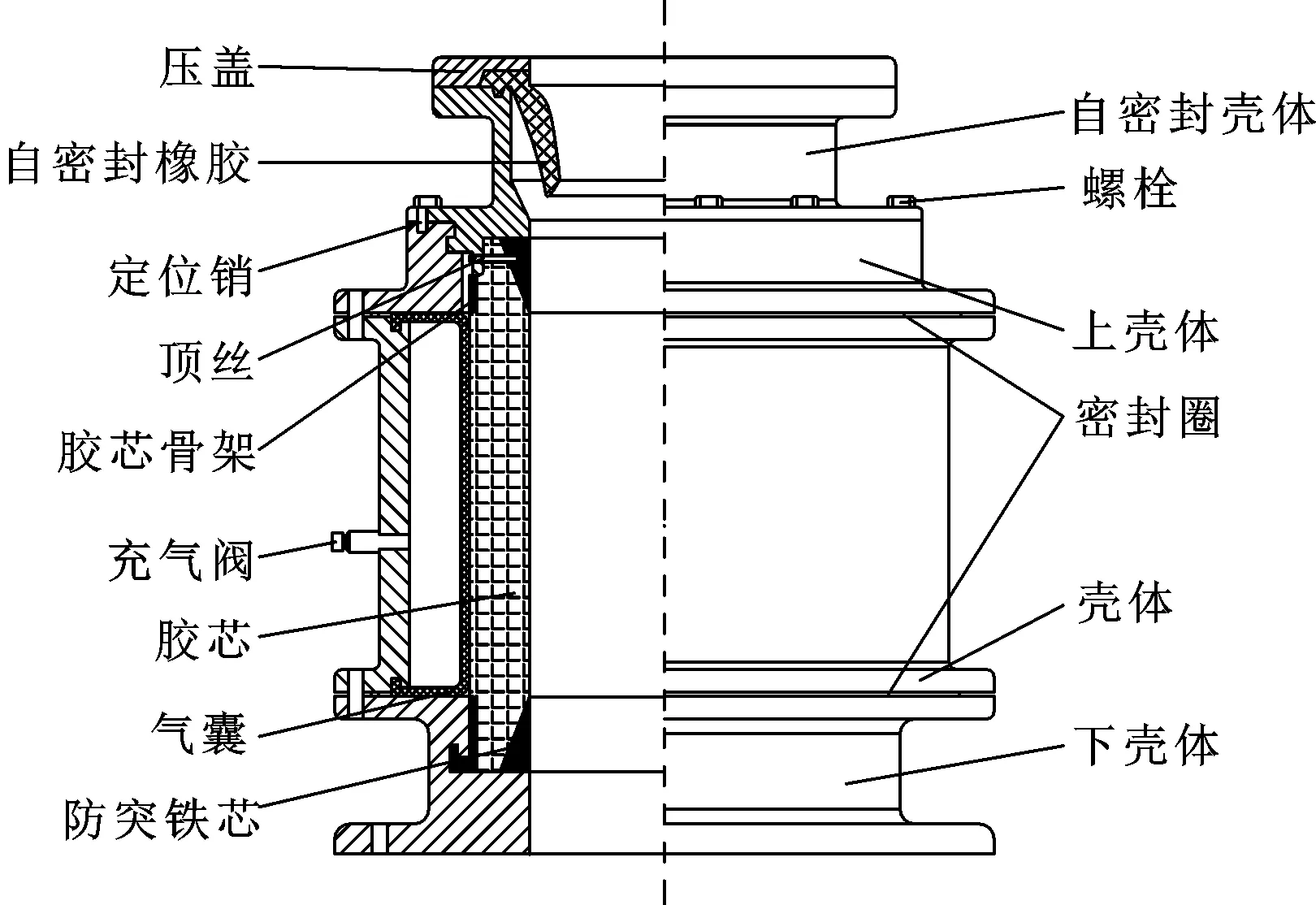
图1 气控环形防喷器结构示意图Fig 1 The schematic diagram of air controlled annular BOP
1.2 气控环形防喷器作业原理
气控环形防喷器利用气体的退让性和特殊的筒形胶芯结构,保证油管接箍顺利通过。其工作原理为:当修井作业需要抱紧油管密封时,操作空气阀,控制系统打入高压气体经壳体上的空气阀进入壳体和气囊之间的空腔,气囊外表面受到高压气体的作用力,压迫胶芯产生大变形抱紧油管,实现密封。当油管接箍通过时,油管接箍使胶芯变形减少,胶芯压迫气囊从而压迫壳体和气囊之间的空腔,利用气体的可压缩性,使油管接箍顺利通过。在作业中产生极其少量的井底废气溢出,被压盖下的自密封橡胶阻拦,封存在自密封橡胶和胶芯之间,进一步保证了井场作业的安全性。气胎式环形防喷器的作业工艺如图2所示。
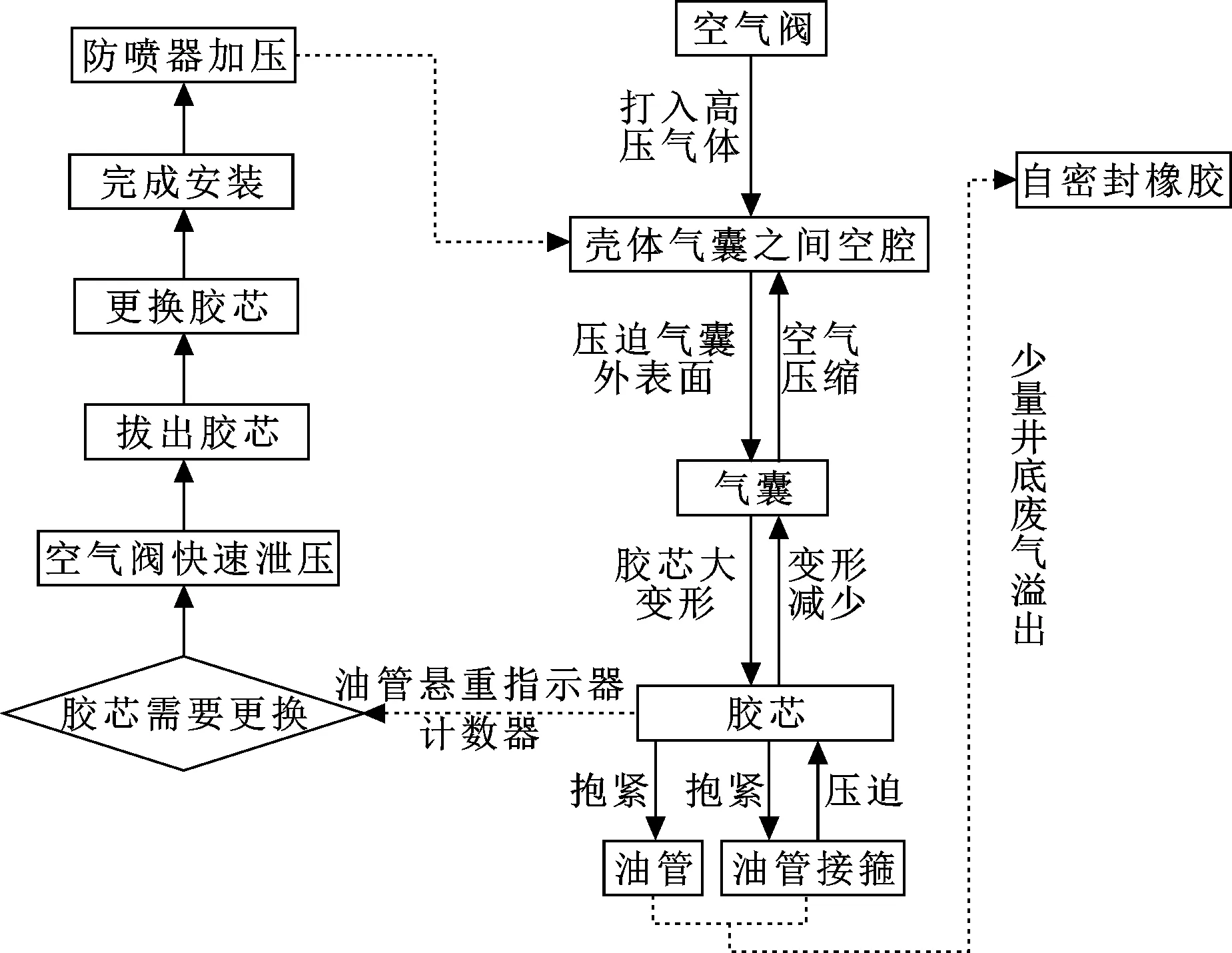
图2 气控环形防喷器作业工艺流程图Fig 2 The flow chart of air forced annular blowout preventer in operation
2 胶芯物理模型建立与变形过程分析
2.1 建立物理模型
通过对防喷器作业工艺的分析,得到防喷器工作过程中主要有4种状态:初始状态、初始变形状态、初始密封状态和完全密封状态,如图3所示。
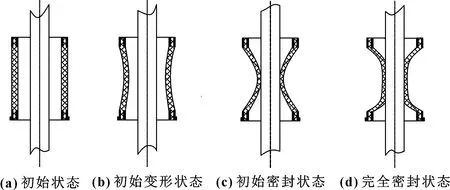
图3 防喷器胶芯变形过程Fig 3 Deformation process of rubber core(a)initial state; (b) initial deformation state;(c)initial sealing state;(d)complete sealing state
初始状态指胶芯未开始工作、控制压力为0时的状态,此时防喷器胶芯无变形,如图3(a)所示;初始变形状态指随着控制压力的增加,胶芯逐渐伸长,产生变形,但并未与油管产生接触的状态,如图3(b)所示;初始密封状态指当控制压力达到一定值,胶芯内侧与油管刚好接触的状态,如图3(c)所示;完全密封状态指胶芯与油管完全接触,胶芯抱紧油管,实现井口密封时胶芯所处的状态,如图3(d)所示。
2.2 变形阶段分析
在胶芯变形过程中,胶芯两侧从两面都不受力到外侧受控制压力,最后到两面均受压力。根据受力情况,可将防喷器胶芯变形分为3个阶段:无变形阶段、自由变形阶段和接触变形阶段。根据胶芯的受力情况建立胶芯的计算模型如图4所示。
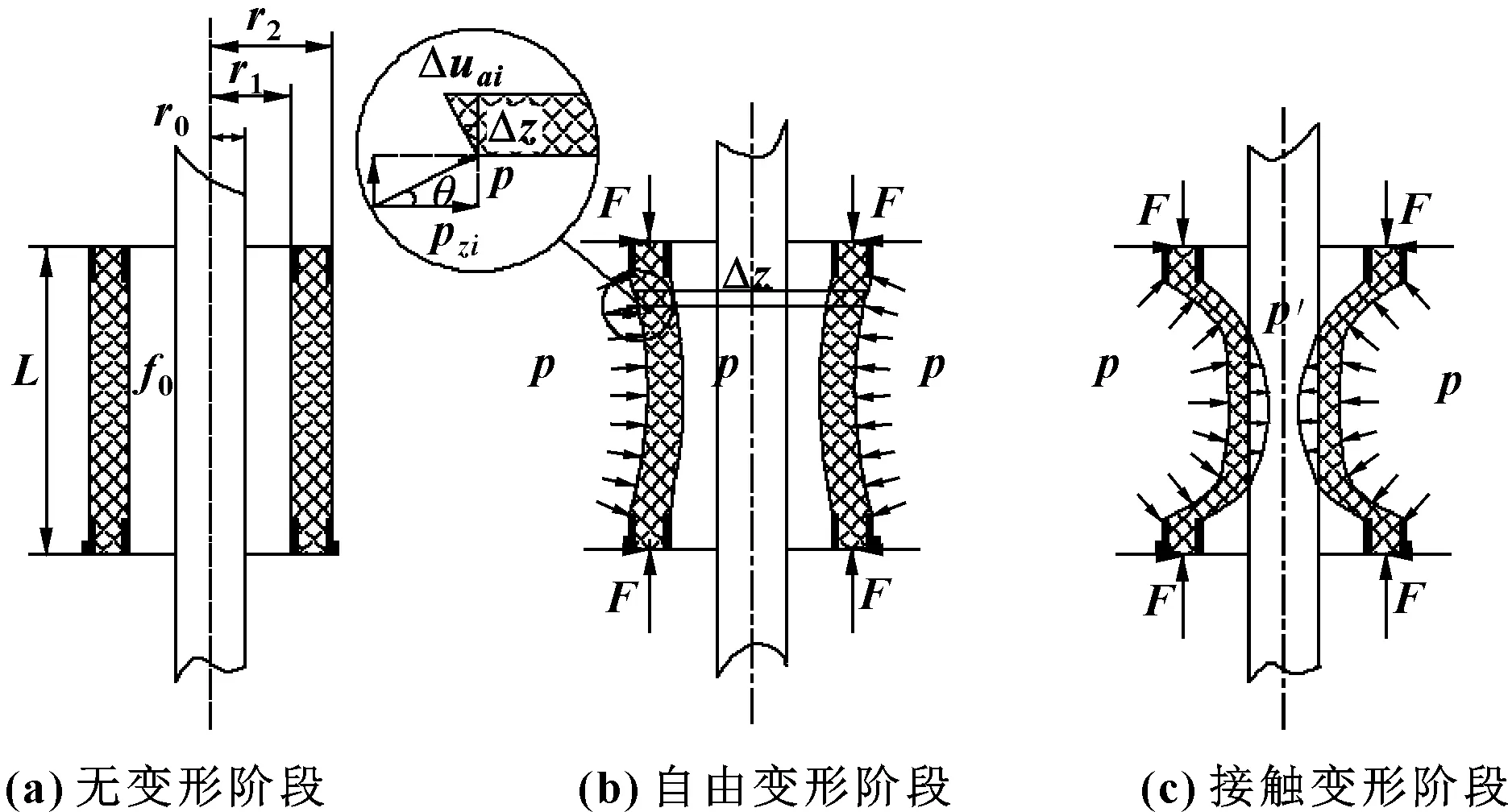
图4 胶芯变形三阶段受力分析Fig 4 Three-stage stress analysis of plastic core deformation(a) no-deformation stage;(b)free deformation stage; (c)contact deformation stage
胶芯处于初始状态时,胶芯外径为r2,内径为r1,胶芯高度为L,油管外径为r0,胶芯和油管间的摩擦因数设为f0,如图4(a)所示。给胶芯施加压力p,胶芯进入自由变形阶段,取微段Δz,受到水平方向上压力大小为pzi,p与pzi的夹角为θ,如图4(b)所示。胶芯两侧固定,受到来自壳体的约束力F。随着控制压力p的增加,胶芯与油管接触,产生接触压力p′,同时由于油管的运动产生竖直方向的摩擦力Fz2,如图4(c)所示。
微段上受到水平方向压力pzi可表示为
pzi=pcosθ
(1)
控制压力p与pzi的夹角θ可表示为
(2)
式中:Δuai表示胶芯微元在压力为pzi时,两微段间的变形量的差,Δuai=uai-uai-1。
3 胶芯变形计算
3.1 胶芯变形方程建立
根据上述对胶芯变形过程和状态的分析,得到了胶芯的受力情况。胶芯变形属于不可压缩的超弹体的大变形,应力与应变属于曲线为单值函数的非线性曲线。试验得到的该胶芯橡胶的应力-应变曲线,如图5所示。
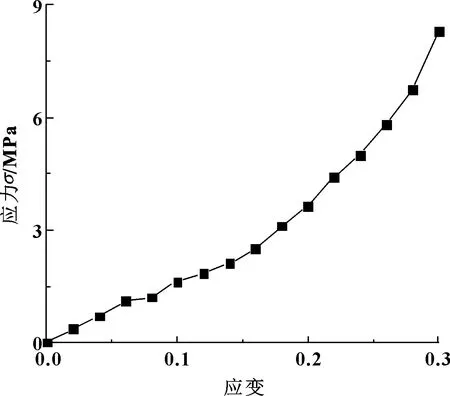
图5 胶芯橡胶的应力-应变曲线Fig 5 The rubber stress-strain curve of rubber-core
防喷器胶芯形状为轴对称结构,来自壳体的约束为对称约束,胶芯在控制压力p作用下产生形变,最终与油管接触,产生接触压力和摩擦力。取胶芯竖直方向微段Δz进行分析,受力分析如图6所示。胶芯变形中任意微段的内外径分别用a、b表示,内外压力分别用p′和pzi表示,Z轴方向的作用力用fz表示。
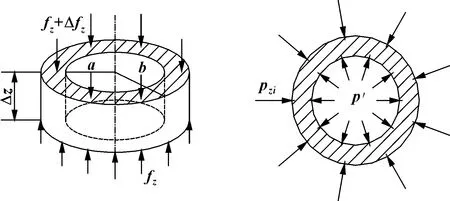
图6 胶芯微段受力分析Fig 6 Force analysis of rubber core micro segment
(3)
环向应力σθ为
(4)
竖直方向的应力σz为
(5)
胶芯Z轴方向的力fz由两部分组成,fz1表示控制压力在Z轴方向的分量,fz2表示油管和胶芯之间的摩擦力,fz可表示为
(6)
式中:k为胶芯和油管的密封系数,当胶芯与油管接触时密封系数取1,当胶芯处于自由变形阶段时,k取0;任一微段胶芯内径为a,a=a+ua;外径为b,b=b+ub。
将式(3)(4)(5)代入橡胶材料的本构方程,得到胶芯的位移方程如下:
(7)
(8)
(9)
式中:E为材料的弹性模量,可以通过图5所示的胶芯橡胶的应力-应变曲线查到应变量并求出;μ为泊松比;k1、k2为与设定胶芯材料、尺寸和所受压力有关的参数,k1=1/(b2-a2),k2=a2p′-b2pzi。
证明 由于μ是紧测度框架, 所以是Parseval框架,再取推论2.2中的E=Ø, 即可得到第一个等式,第二个等式是显然的。
3.2 迭代程序推导
在胶芯分析过程中,将胶芯分成若干微段,采用迭代的方法分析和计算胶芯不同阶段受力和变形量,通过积分和微分的方法把复杂的非线性加载过程转化为微段厚壁筒进行分析计算,对迭代过程的求解设计如图7所示。
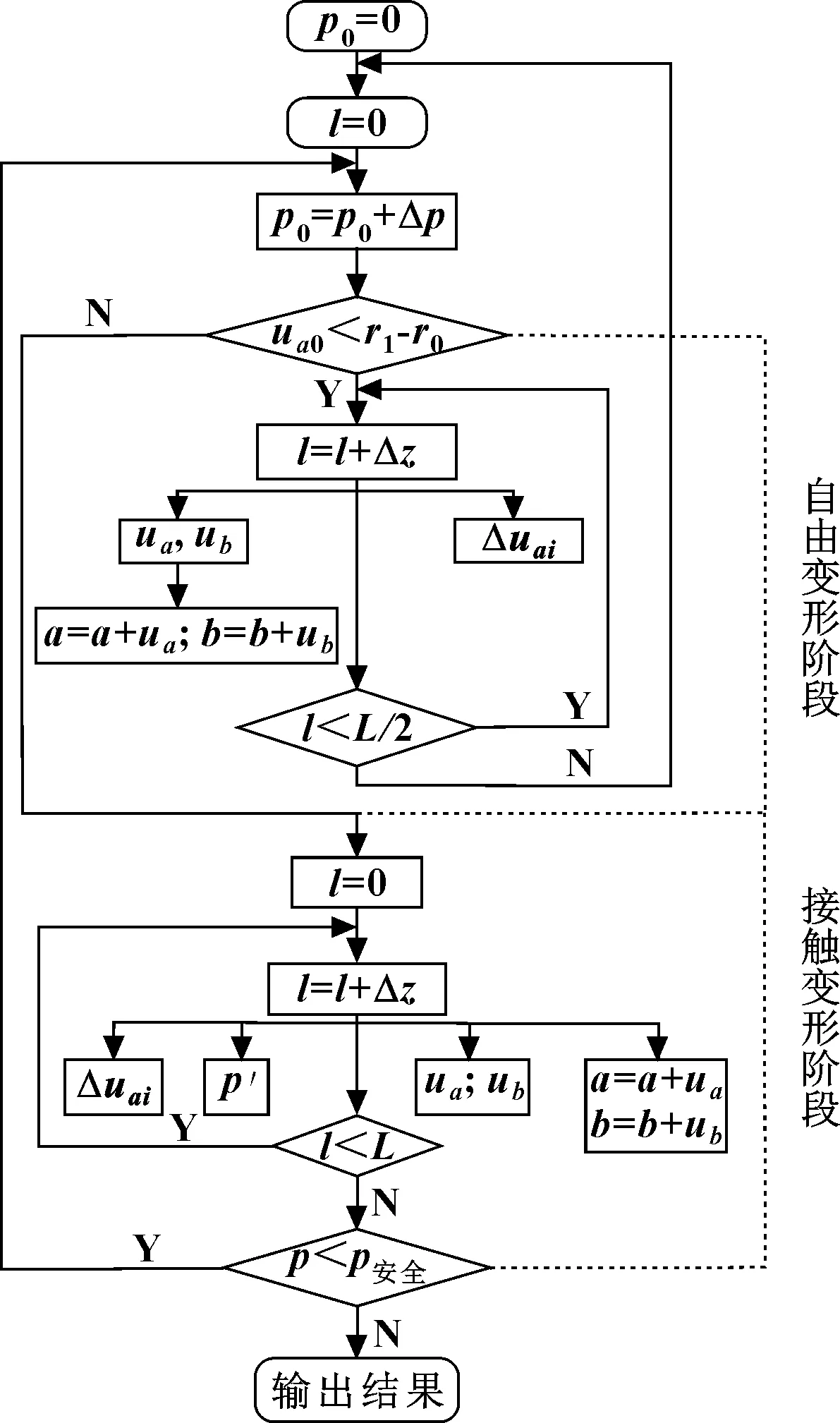
图7 胶芯计算流程图Fig 7 The flow chart of rubber core calculation
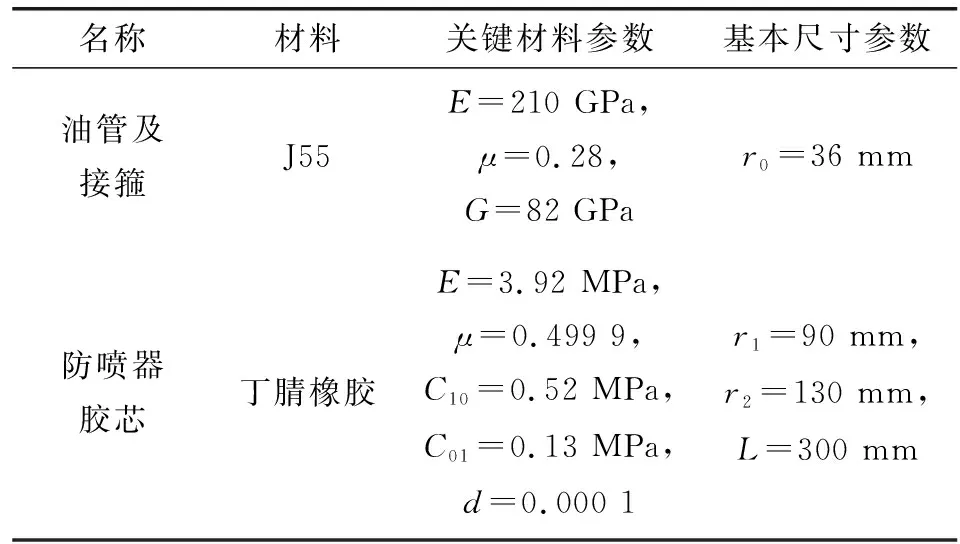
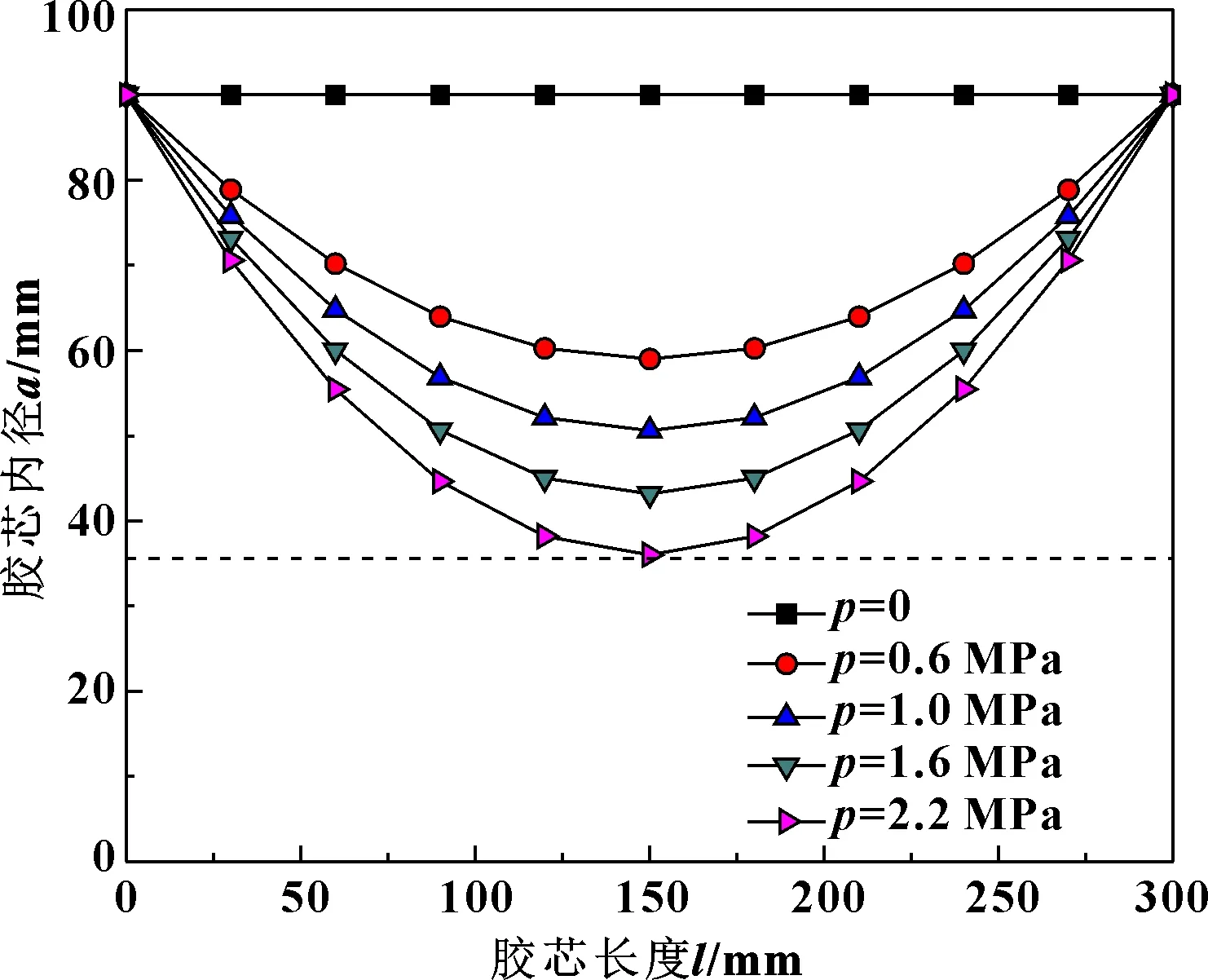
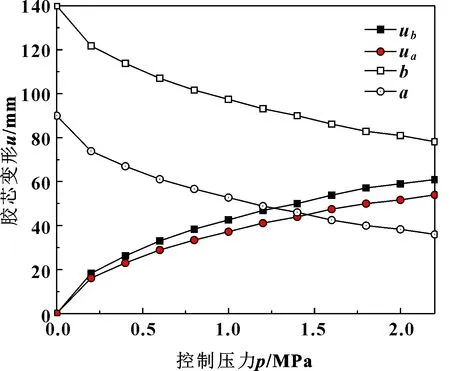
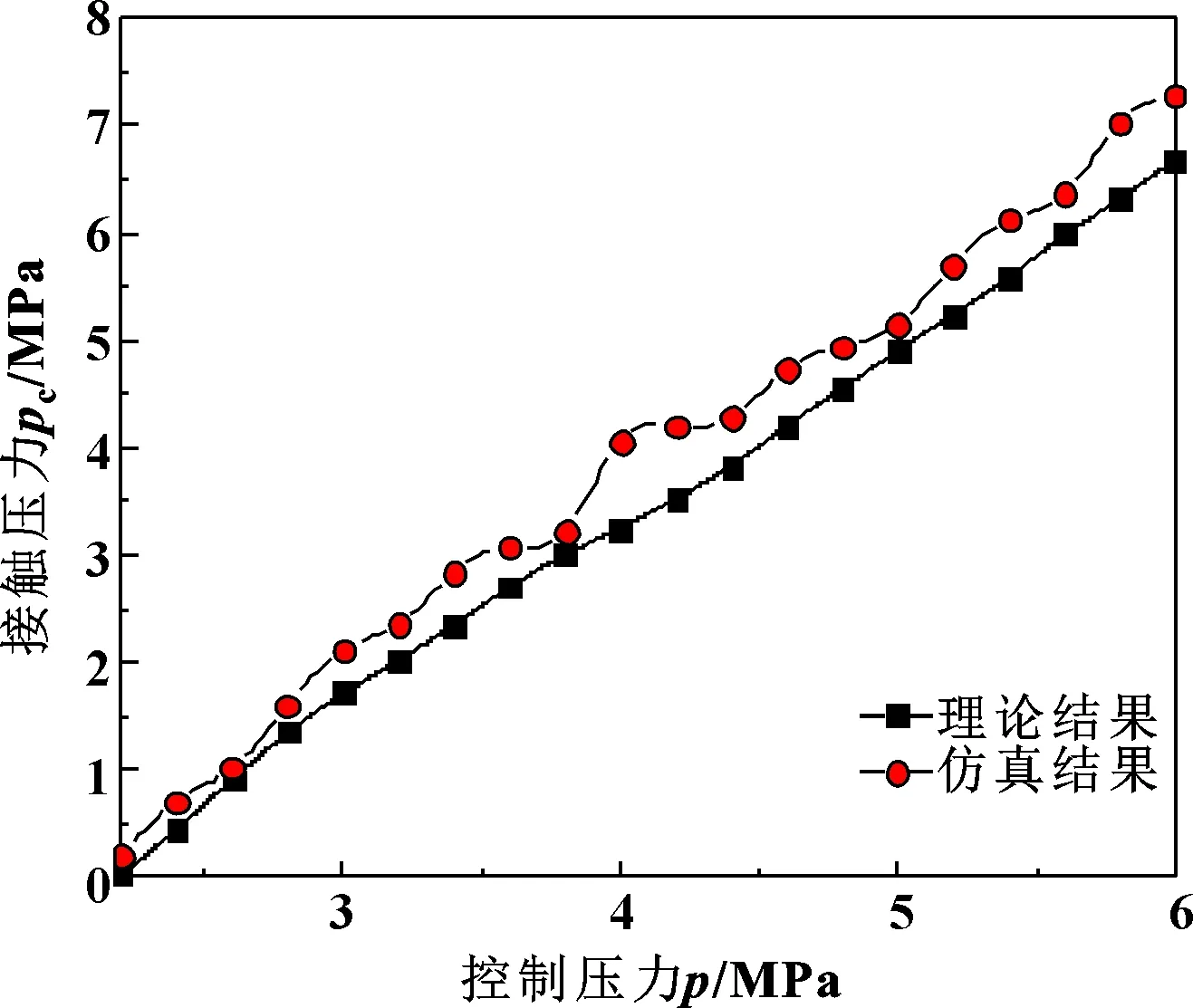
随着控制压力p的增加,胶芯开始产生变形,内外径不断改变,当ua 根据上述分析,设定边界条件,求解胶芯接触压力和变形量随控制压力的变化关系,根据胶芯受力状态的不同,将胶芯受力分为2种情况进行分析,即自由变形阶段和接触变形阶段。 (1)自由变形阶段 在自由变形阶段胶芯与油管无接触,密封系数k=0,边界条件为 (10) 此时式(7)可以表示为 (11) 对式(11)进行积分得到: (12) 式(12)中,当r确定时,依然存在pzi和ur2个未知量,为了求解变形量,首先计算当θ=0时,胶芯变形量ur0。然后结合式(2)和(12)求解2个未知量θ和uri。 根据上述步骤,得到r=a和r=b时变形量与压力关系方程: (13) 因此通过Δz叠加可以得到每一微段上胶芯内外径变形量随控制压力变化方程。 (2)接触变形阶段 在此阶段,胶芯与油管接触,接触系数k=1,边界条件为 (14) 此时,对式(7)积分: (15) 根据式(9)确定常数C=0,同时得: (16) 根据边界条件得: (17) 与胶芯自由变形阶段相同,式(16)和(17)存在4个未知数,所以取θ=0时计算变形量和压力,然后结合式(2)得到每一微段的变形量和接触压力p′的变化。 选取防喷器胶芯和油管基本参数如表1所示。 表1 胶芯和油管基本参数Table 1 The basic parameters of rubber core and oil tube 设定初始控制压力为0,压力增量Δp=0.2 MPa,安全压力p安全=6 MPa,迭代长度Δz=2 mm,油管和胶芯之间的摩擦因数取0.1,计算得到自由变形阶段,胶芯变形关系随控制压力变化关系如图8所示。可知:随着控制压力的增加,胶芯变形量越来越大,且中间变形量最大,两侧变形量逐渐减小;当控制压力为0时,在整个长度上胶芯内径为90 mm,无变形;当控制压力为2.2 MPa时,胶芯内径变为35.78 mm,与油管外径接近,如图8中虚线所示,此时,自由变形阶段已经结束。 图8 胶芯内径随控制压力变化曲线Fig 8 Change curves of internal diameter of rubber core with control pressure 在胶芯自由变形阶段,取控制压力方向θ=0的微段,得到不同压力作用下的胶芯内外径及变形量如图9所示。随着控制压力的增加,胶芯内外径a、b逐渐减小,变形量ua、ub逐渐增加。由于胶芯在控制压力作用下整体伸长,厚度变小,所以外径变形量ub大于内径变形量ua,且差距越来越大。当自由变形结束时,ub和ua的差为6.82 mm,此时胶芯外径为78.96 mm。 图9 胶芯内外径及变形量随压力变化关系Fig 9 Variation of internal and external diameter and deformation of rubber core with control pressure 利用有限元的方法对胶芯进行模拟分析,并在ANSYS软件中建立有限元模型。选取73.02 mm的油管进行分析,油管接箍外径尺寸为93.17 mm,长度为133.35 mm,油管和胶芯主体的参数如表1所示。对胶芯油管进行网格划分,设定胶芯网格大小为5 mm,油管网格大小为10 mm。最终得到在不同控制压力下的接触压力的理论计算与仿真计算结果如图10所示。 图10 接触压力随控制压力变化关系Fig 10 Relationship between contact pressure and control pressure 从图10可以看出:随着控制压力的增加,接触压力不断增加,仿真结果与理论结果趋势相同,且仿真结果略大于理论结果。当控制压力为2.2 MPa时,仿真得到接触压力为0.19 MPa,但理论计算认为胶芯和油管刚开始接触,接触压力为0,出现此误差的原因是由于理论计算时,迭代选用压力差较大,由图8可知,控制压力为2.2 MPa时,胶芯内径大小已经小于油管外径,此时接触变形已经开始,但理论计算不能准确给出,所以在下一轮计算中直接取临近的2.2 MPa为接触变形起始压力。同样,由于理论分析选取压力和长度梯度大,在每个压力梯度下,认为所取微段变形为线性,存在计算误差,通过每次迭代导致误差累积,所以造成仿真得到接触压力略大于理论值,且差距趋势越来越大。 (1)将防喷器工作过程分为初始状态、初始变形状态、初始密封状态和完全密封状态,并根据胶芯的受力情况,划分胶芯变形过程为无变形阶段、自由变形阶段和接触变形阶段。 (2)在胶芯自由变形阶段,随着控制压力的增加,胶芯变形量越来越大,胶芯外径变形量大于内径变形量,且两变形量之差不断累积;在接触变形阶段,胶芯内径保持不变,且与油管间接触压力不断增加。 (3)采用胶芯变形理论方法计算的接触压力虽存在一定的累积误差,但与仿真得到的接触压力变化趋势相同,验证了胶芯变形理论计算方法的正确性。3.3 不同阶段胶芯变形量和接触压力求解
4 计算结果与分析
4.1 计算结果分析
4.2 理论与仿真结果对比
5 结论

