归纳逻辑程序设计综述

戴望州 周志华

(计算机软件新技术国家重点实验室(南京大学) 南京 210023)

规则学习是机器学习中以符号规则为模型表达方式的一个分支，主要属于符号主义学习的内容.在文献[1]中有对规则学习的基本介绍，本文主要关注以一阶逻辑(first-order logic， FOL)为表达语言的归纳逻辑程序设计(inductive logic programming，ILP)[2].一阶逻辑是一种形式系统[3].与只能陈述简单命题的命题逻辑相比，FOL引入了谓词、函数和量词等更多词汇，它可以通过谓词来量化地陈述命题，因此也被称为一阶谓词演算.

基于文献[1]的界定，ILP指以FOL归纳理论为基础，以FOL规则为模型的机器学习方法.与其他种类机器学习方法相比，ILP能够在学习过程中以FOL规则的形式引入复杂领域知识，并能自然地处理学习问题中的复杂推理.此外，它学得的模型具有较好的可理解性，这使得用户和领域专家能够方便地对学习成果进行解读和研究.

1 发展历程

“归纳逻辑程序设计”的命名来自于Muggleton[2]于1991年发表的奠基性论文以及同年召开的第一届国际归纳逻辑程序设计研讨会，它是如今国际归纳逻辑程序设计会议(International Conference on Inductive Logic Programming)的前身.

20世纪七、八十年代出现并流行的专家系统[4]极大地推广了人工智能实际应用.专家系统的知识库一般由一组符号逻辑规则构成.早期专家系统中的规则必须由领域专家提供，这不仅成本高，在许多任务中还由于专家知识难以总结或专家不愿分享知识而难以完成，形成了所谓“知识工程瓶颈”.为了突破这个瓶颈，出现了许多以符号逻辑表达语言的机器学习方法[1].

一般来说，此类方法存在3种局限[2]：1)它们学得的模型一般为命题逻辑规则.受限于模型的表达能力，难以描述对象之间的“关系”(relation)，而在许多任务中关系信息非常重要.2)命题学习的输入一般为属性-值(attribute-value).许多领域知识难以被表示为这种形式，导致学习过程不易利用领域知识.3)命题规则只能由一组固定的属性特征所对应的原子构成，学习过程不能自主地对原始特征空间进行变换以弥补其不足.

为了解决这些问题，Muggleton[2]指出应当使用表达能力更强的FOL作为机器学习的形式化语言.逻辑程序(logic programming)[5]作为计算机技术中应用最广泛的FOL系统之一，理所当然地成为了首选.由于机器学习是一种从数据中自动“归纳”(induction)的方法，因此它与逻辑程序设计结合而诞生的学科便被命名为“归纳逻辑程序设计”.

事实上，早在20世纪70年代就已出现一些关于FOL归纳理论的先驱性工作[6-9]，例如对FOL归纳学习可行性的证明，为ILP的出现奠定了基础.其中Plotkin[6]提出的“最小一般泛化”和“相对最小一般泛化”后来成为ILP的基础运算.20世纪80年代中期，开始出现Marvin[10]等初步运用FOL归纳的机器学习算法.20世纪80年代后期出现了许多关于FOL归纳理论的研究，例如Muggleton的逆归结[11-13]以及Rouveirol和Puget[14]的工作等.Muggleton[12]首次提出使用FOL归纳来实现一阶谓词发明[12]，使得机器学习过程能自动对不够完善的背景知识进行弥补，这期间也出现了最早的ILP系统Cigol[12].

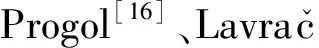
由于逻辑程序无法直接描述不确定性，ILP难以对带噪声的数据进行学习.为了解决此问题，Dantsin[32]首次在逻辑程序中引入概率分布，提出了概率逻辑程序(probabilistic logic programming， PLP)，Poole[33]研究了PLP中的概率推断，Sato[34]则在Dantsin[32]的基础上为PLP定义了严格的FOL语义.2004年De Raedt[35]等人提出了以PLP为模型的机器学习框架，它是ILP的一种概率扩展，被称为概率归纳逻辑程序设计(probabilistic inductive logic programming， PILP).在这些工作的基础上，研究者们提出了众多PLP模型[36-43]与PILP算法[44-48].

2010年至今，ILP领域的研究又取得进一步发展.例如在传统的ILP理论方面，研究者们提出采用二阶逻辑诱导来进行FOL归纳[49-50]，此类ILP方法在谓词发明和学习递归规则的能力上取得了突破；PILP领域依旧十分活跃[51-58]，被成功应用在自然语言处理和生物信息学等许多兼具不确定性与复杂领域知识的实际任务中[59-64]；此外，随着近年来深度学习的崛起，为了进一步提高ILP的学习效率，研究者们开始尝试在ILP中嵌入可微构件[65-66]，并取得了一定成效.

2 基本内容

在不做特别说明的情况下，本文将以汉字、阿拉伯数字和小写英文字母开头的词代表谓词、函数与常量，以大写英文字母开头的词代表变量和FOL公式，并省略FOL公式中的全称量词“∀”.

不含连接词的FOL公式被称为原子公式(atom)，例如“奇数(X)”；原子公式及其否定式被称为逻辑文字(literal)，例如“奇数(X)”；当公式中不含变量时被称为“具体的”(grounded)，具体的原子公式被称为具体事实(ground facts)，例如“奇数(3)”.

ILP模型是由逻辑公式组成的集合：

A←B1∧B2∧…∧Bn.

(1)

其中，A和Bi分别为FOL原子和文字.一般称这种公式为FOL规则，其中“←”右边的部分是有限个文字的合取，被称为规则体(body)，表示此规则的前提；“←”左边的A是一个FOL原子，被称为规则头(head)，表示规则的结果；“←”是数理逻辑中的蕴涵符，表示“推出”关系；n≥0为规则长度.该规则表示：“若B1,B2,…,Bn均成立，则A也成立”.

FOL系统的语义被体现在FOL公式的赋值(assignment)中.最基本地，可以对每一个具体事实进行赋值，令其为true或为false.然后FOL系统会按照一定规则进行演算，从而得到其他公式的真值.若存在一种赋值方使得某公式为true，则称此公式为可满足的(satisfiable).公式(集)Γ与T之间的可满足性被称为“语义蕴涵”(entailment)，记为“ΓT”.它表示一切令Γ为真的赋值也使得T为真.公式(集)之间还存在一种“语构蕴涵”(implica-tion)关系，记为“ΓT”，一般读作“Γ可推出T”.它表示Γ可以凭借FOL公理证明出T.

对于一般的形式系统，这2种蕴涵关系并不等价.若一个形式系统有(ΓT)→(ΓT)，则称该系统为“完备的”(complete)[3].对机器学习而言，若令Γ和T分别表示假设(hypothesis)和训练样例(example)，那么对完备的学习算法来说，其假设空间必然包含所有满足训练样例的假设.

2.1 学习任务

ILP主要关注“概念学习”[1]，即学习一个关于目标概念(target concept)的描述(该描述也可视为一个单类别分类器).学习过程的输入是一组关于目标概念的样例和背景知识(background knowledge)，输出为一个满足所有样例的假设，即学得模型.本文将背景知识记为B，假设模型记为H，训练样例记为E=E+∪E-，其中E+和E-分别代表正负样例.那么，概念学习任务可以用FOL语言形式化为

B∪HE.

(2)

对于传统的概念学习问题来说，B和E的形式一般为属性-值数据集，E中的每个示例(instance)均被表示为一个特征向量，H可以是任何形式.而对ILP来说，这里的B,E和H均为逻辑程序[5].通常情况下，E是一组关于目标概念的具体事实；B则是一系列关于原始概念(primitives)的具体事实；H是一个FOL规则集，每条规则均由原始概念组成.

表1[1]展示了一个ILP任务所使用的数据集.其中的原始概念为瓜与瓜之间在某些属性上的比较关系；每行是一个关于原始概念的具体事实；目标概念是“更好”.此类数据集中的条目不再是关于某一个对象的特征或标记，而是多个对象之间的“关系”.故而ILP的任务属于关系学习(relational learning)[1]，此类数据集也被称为关系型数据集(relational data).

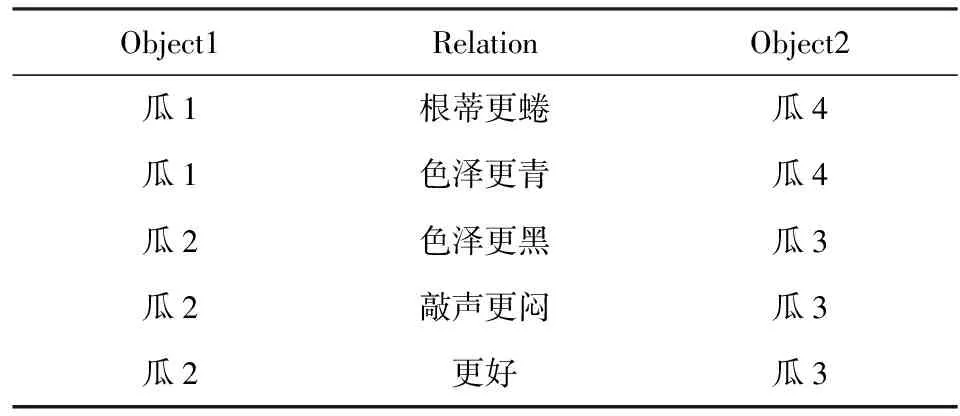
Table 1 An Example of Relational Dataset表1 关系型数据集

对象间的关系可能十分复杂，例如表1中的目标概念“更好”便是一个递归关系：

更好(X,Y)←更好(X,Z)∧更好(Z,Y).

“归纳逻辑程序设计中”的“归纳”是逻辑系统中演绎(deduction)推理的逆过程.“演绎”指从一般规律出发推演出具体结论的特化(specialization)过程.譬如式(2)自左向右所描述的便是以B∪H作为前提，最终推导出结论E的演绎推理.而“归纳”则与演绎相反，它需要从具体的样例出发，总结出一般规律以概括这些样例，故而它是一个泛化(generalization)过程.换言之，ILP可视为FOL中演绎推理的逆运算.

表2总结了FOL中常见的演绎和归纳运算.大部分ILP方法[11-12,14-16,67]均源自这些归纳运算.此外，还有一些ILP系统试图先将关系型数据转化为属性-值数据，再使用命题学习技术来获取FOL规则[25,68-70].本节将简要介绍这些基本的ILP方法.

Table 2 Deduction and Induction Operations in FOL表2 FOL中的演绎与归纳运算

2.2 最小一般泛化

Robinson[71]提出的“合一”(unification)是最简单的FOL演绎运算，其目标是将逻辑变量替换(substitute)为常量以使2个逻辑文字相等，这可以直观地理解为对背景知识B进行“查询”[1].例如当B中存在事实“A1=a(1,2)”时，若欲推出“A2=a(X,2)”的赋值，只需将A2与A1合一即可得到一个替换“θ={X=2}”使得A2θ=A1，即当X=2时A2为true.合一过程中同时存在多种可行的替换时，往往希望通过替换最少的变量来使合一成立，这被称为“最一般合一”(most general unification, MGU).

合一的逆运算是由Popplestone[72]所提出的“泛化”运算，它反过来将原子公式中的常量替换为变量以使逻辑文字变得更一般.MGU的逆运算是Plotkin[6]提出的最小一般泛化(least general gener-alization, LGG)，它能够通过替换最少的常量使得FOL公式的泛化性最强.例如，若B中同时存在2条具体规则：

1) 更好(瓜1,瓜2)←色泽更黑(瓜1,瓜2).

2) 更好(瓜3,瓜2)←色泽更黑(瓜3,瓜2).

LGG可将它们中的常量代换为变量，以得到一条能够概括这2条规则的一般规则：

更好(X,瓜2)←色泽更黑(X,瓜2).

在ILP问题中，B∪E一般为关于原始概念和目标概念的具体事实，不存在可供LGG直接泛化的具体FOL规则.因此Plotkin[7]提出先用B∪E来生成关于目标概念的具体规则，再使用LGG对它们进行泛化.例如根据表1中的所有事实即可构造出具体规则：

更好(瓜2,瓜3)← 色泽更黑(瓜2,瓜3)∧

根蒂更蜷(瓜3,瓜4)∧

…

这种根据全体B∪E生成的具体FOL规则后来被称为饱和规则(saturation)[14]；由于针对饱和规则进行的LGG与B∪E相关，所以这种LGG被称为相对最小一般泛化(relative LGG, RLGG)[7].

Plotkin[7]证明对于任意FOL文字集合S，只要它不包含矛盾文字——即不存在A使得A∈S且(A)∈S，则可通过LGG得到至少一条可满足S的非空FOL规则R.当B与E分别为由n和m个具体事实构成的集合时，RLGG可以求出所有满足式(2)的H，但最坏情况下学得的规则将包含O((n+1)m)个文字[8].

但是，若B中包含形式不受限制的FOL公式，则(R)LGG运算无法保证完备性[8].此外，若目标概念必须由多条FOL规则才能表示，则(R)LGG将无法学得正确的模型[8].因此，一般情形下基于(R)LGG的ILP不满足完备性.

基于RLGG归纳的代表性ILP算法是Muggleton和Feng[24]提出的Golem，它有较高的学习效率，是早期应用最广泛的ILP系统之一.

2.3 逆归结

在合一的基础上，Robinson[71]提出了归结原理(resolution principle)以处理更复杂的多步演绎.它试图借助MGU运算来找到背景知识与演绎目标中相反的项，然后对它们进行消解.将归结原理的过程逆转过来便构成一种FOL归纳运算.Muggleton[11-12]首次将该方法应用于机器学习，并将它命名为逆归结(inverse resolution).文献[1]中对FOL中的归结原理与逆归结有详细介绍.

图1展示了4种逆归结运算.其中，p，q和r代表规则头中的原子公式；A，B和C代表规则体中的FOL文字集合；每种运算的上下2行分别为逆归结的输入与输出；二者间的箭头代表逆转后的归结原理[1].

Fig. 1 Four kinds of inverse resolution operators图1 4种逆归结运算

逆归结首次实现了FOL归纳中的谓词发明[12]，它在学习过程中能够自动构建背景知识B中未出现的概念，例如图1内构(intra-construction)与互构(inter-construction)运算输出的新原子q和r.新发明的谓词可作为新的“原始概念”被用于构成H.直观来看，谓词发明是当B中的原始概念不足以简洁地描述目标概念时，ILP将某些逻辑文字的组合归纳为一个事先未定义的新概念，并将之用于构建H，以减少H的规则条数或者规则长度.换言之，谓词发明能够对B所定义的领域结构进行补充，它可以帮助用户对领域建立新的认识[2].

对命题规则学习而言，只需吸收与内构2种运算即可保证逆归结的完备性[11]，但对ILP该结论并不成立[13].

基于逆归结的Duce[11]和Cigol[12]是最早实现的ILP系统，它们分别被用于命题规则学习和ILP任务中，后者第一次实现了FOL中的谓词发明.逆归结的缺点在于内、互构运算会不断地对规则集进行扩充，而得到的新规则又会作为下一阶段逆归结的输入，从而导致生成更多规则.此外，这些新谓词、新规则的可满足性在学习过程中很难验证.因此在缺乏有效的剪枝策略时，逆归结运算会造成组合爆炸.所以Cigol的效率远不如基于RLGG的Golem[24].

2.4 逆语构蕴涵

2.2节和2.3节讲述的2种FOL归纳运算均无法满足完备性，根本原因在于它们所采用的基础泛化运算LGG与FOL中的语构蕴涵关系“→”并不等价[15].

“P是Q的LGG”仅代表公式P可以通过变量替换与Q合一，不妨将这种关系记为“Pθ⊆Q”，其中θ代表合一时使用的变量替换.而语构蕴涵关系“P→Q”的本义是“P可推出Q”.事实上，若Pθ⊆Q则必有P→Q；反之则并不成立.例如，考虑2个FOL公式：

P≡p(f(X))←p(X)，
Q≡p(f(f(X)))←p(X)，

使用f(x)替换掉P中的X得到:

R≡p(f(f(x)))←p(f(X)).

再对P，R使用三段论(modus ponens)[3]即可证P→Q，即P蕴涵Q；但是，P却无法通过任何变量替换来使之等价于Q.也就是说，Q无法通过LGG得到P.因此LGG不能保证FOL归纳的完备性.

可以看到，上例中从P到Q的推导过程只利用了规则P自身，因此Q被称为由P“自归结”(self-resolution)得到.为了补全LGG运算，Muggleton[15]给出了完备语构蕴涵的3种情况.在FOL中，若P→Q，则要么Q恒真；要么Pθ⊆Q；要么∃R(θR⊆Q)，其中R可通过对P不断进行自归结得到.

依据该结论，Muggleton[15]给出了对FOL归纳完备的逆语构蕴涵(inverse implication)运算，它在使用LGG对具体规则进行泛化的同时，还需对所有LGG输出的中间结果R进行逆归结，以找到所有可通过自归结得到R的规则R′.根据上面的结论，只需令H=R∪R′即可保证FOL归纳的完备性.

事实上，在FOL中能够进行自归结的公式均为递归公式，即类似于“p(f(X))←p(X)”这样规则体与规则头中出现相同谓词的FOL规则.在逆语构蕴涵出现之前，基于(R)LGG与逆归结的ILP无法处理此类递归概念.

遗憾的是，找寻递归语句的逆自归结公式是一个不可判定(undecidable)[3]问题，所以完备的逆语构蕴涵只停留在理论阶段，并未形成真正的算法.目前为止，基于逆语构蕴涵思想的ILP方法仅有Idestam-Almquist[67]在对其进行放松后提出的逆T-语构蕴涵.

2.5 逆语义蕴涵

2.4节介绍的(R)LGG、逆归结和逆语构蕴涵的目标均是对可证关系(即“→”)进行逆转，它们很难保证FOL归纳的完备性.为了解决“→”带来的问题，Muggleton[16-17]提出应当从FOL语义——即B∪H对E可满足性的角度来进行归纳.

基于该想法，Muggleton[16]提出了语义蕴涵“”的逆运算——逆语义蕴涵(inverse entailment).通俗地理解，它基于“逆否命题与原命题等价”这一原则，将式(2)等价地转化为

B∪EH.

(3)

这种做法巧妙地将原归纳问题化归为一个演绎问题：即通过B∪E来推导出可能的H，最后只需将推导出的结果取反，即可得到原问题所求解的H.

具体来说，在应用逆语义蕴含时，先要将所有样例E取反得到E，再对B∪E进行演绎得到⊥.由于演绎推理得到的结果只能是一组具体事实，因此不能将⊥直接取反作为H.不过，若H存在，则由式(3)可知(⊥H)∧(H⊥).根据“∧”的右半部分，只需先将⊥中所有具体事实取反，再进行泛化即可得到H.也就是说，逆语义蕴涵的步骤是“先特化、后泛化”.

理论上，对形如式(1)的FOL规则集合，逆语义蕴涵能保证归纳的完备性[17]，但这在实际操作中却并不简单.一个主要原因是在进行式(3)中的演绎推理时难以保证得到的⊥形式和数量足够丰富.例如对2.4节提到的递归公式，它们通过自归结演绎得到的事实可能有无穷多个.因此一旦B中存在递归规则，就无法保证获得足够大的⊥并泛化出一切满足式(3)的H.所以，在实现过程中往往要引入一些先验来对⊥的形式和演绎过程进行约束，在保证逆语义蕴涵的效率的同时使之尽可能完备.

最早基于逆语义蕴涵的ILP方法是Muggleton[16]于1995年提出的Progol，它通过设置超参数来约束⊥的大小；并使用模式声明(mode declaration)来保证⊥中事实的形式足够丰富.而在对⊥进行泛化时，Progol还提出使用精化算子(refinement operator)[18]来对搜索过程进行剪枝来提高学习效率，避免在进行泛化时出现冗余规则.

2.6 命题化

基于命题化方法[68]的ILP试图先将关系型数据转化为属性-值数据，然后再使用命题规则学习技术来建立模型.命题化数据中的特征为FOL文字或FOL文字构成的合取式，因此命题化方法学得的“命题规则”事实上仍旧是FOL规则.

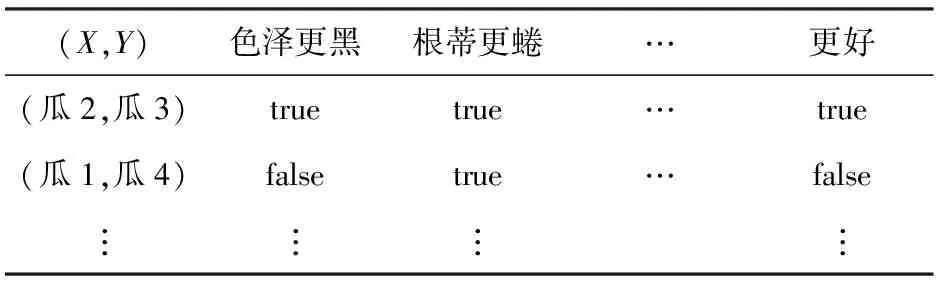
Table 3 An Example of Propositionalized Dataset表3 命题化数据集

与其他ILP方法相比，基于命题规则学习的命题化方法既能更自然地处理领域中的噪声，又拥有更高的学习效率.但它在生成数据集时需要耗费一定时间.此外，它的假设空间十分依赖于关系型特征的构造，若领域中的关系过于复杂，则需要生成大量的关系型特征才能保证学得足够好的H.此外，基于命题化方法的ILP不能学习递归规则，因此无法保证FOL归纳的完备性.所以，命题化方法一般被应用于以个体为中心的领域[68]，即目标概念只描述个体属性而不涉及个体间关系的领域.

2.7 ILP的PAC可学习性

基于命题规则学习的PAC可学习性结论[19,73]，Page和Frisch[74]证明了单条不含函数符且非递归的一类特殊FOL公式通过LGG是PAC可学习的.此类FOL公式形如式(1)，但所有出现在{B1,B2,…,Bn}中的FOL变量必须也在A中出现.

上述结论只适用于单条FOL规则学习，为了研究规则集可学习性，Džeroski等人[20]定义了一类“确定子句”来对FOL规则的形式进行约束.这里的“确定”代表对于式(1)规则体中的每个文字Bi：若Bi中存在一个变量X从未在其之前的文字A,B1,…,Bi-1中出现，那么对X来说，一旦A,B1,…,Bi-1中除X以外的变量取值确定，则X的取值也能唯一确定.他们证明了对于符合某些简单概率分布、不含函数符且无递归的FOL确定子句集，可在多项式时间内将其扩张为PAC可学习的命题规则集.

若不对目标概念所服从的概率分布进行假设，Džeroski等人[21]证明不含函数符、无递归且每条规则长度有限的一类FOL规则集是PAC可学习的.但此时学习算法的时间复杂度关于目标概念中最大规则的长度呈指数级增长.Cohen[22]进一步去掉了该结论中对“非递归”的要求，但增加了一些额外假设，例如每个FOL变量在规则中的出现次数有限.

虽然陆续有理论证明某些形式受约束的FOL规则集PAC可学习，但Kietz[23]证明，一般形式的FOL公式集不是PAC可学习的.这是因为ILP在搜索H的过程中必须不停地检测它是否与B∪E冲突，而对于形式不加约束的B和E，这是NP-hard问题.

这些结果均说明FOL规则学习在本质上比命题规则学习更加困难.Cohen与Page[75]总结了ILP关于PAC可学习性研究的大部分结论.他们指出，FOL模型远比命题规则复杂，所以不能仅以命题规则学习的样例数与规则复杂度来衡量FOL模型的可学习性，而应当试图从FOL模型本身的角度对可学习性进行探索.

3 研究进展

第2节所介绍的基本ILP方法有3个主要局限：1)除了逆归结以外，其他实用性更强的ILP方法均无法直接实现谓词发明，并且对递归规则的学习效率较低；2)受FOL语言表达能力的限制，大部分ILP方法不能在数据带噪声的情况下进行学习；3)由于ILP的假设空间结构十分复杂，进行高效的学习有相当的困难.

近年来，ILP研究者们在这3个问题上均取得了进展.其中以元解释学习(meta-interpretive learning, MIL)[50]为代表的二阶诱导方法较好地解决了谓词发明和递归规则学习的问题；概率归纳逻辑程序(PILP)[35]则对ILP进行了概率扩展，使之能够应对学习问题中的噪声；还有一些工作尝试在ILP中嵌入神经网络等可微构件[65-66]，利用梯度下降和误差反向传播算法来加速ILP学习.本节将对这些方向中的代表性工作进行简要介绍.

3.1 二阶诱导推理

诱导推理(abductive reasoning)[76]是在演绎和归纳之外的另一种逻辑推理形式.它能根据背景知识为已观测事实找到一种合理的原因作为解释，因此也被称为“溯因”推理.例如，若背景知识中存在如下3条FOL规则：

1) 出汗(X) ←觉得热(X),

2) 觉得热(X)←天气热,

3) 觉得热(X)←运动后(X).

那么，在观测到“出汗(张三)”为true时，根据第1条规则便能诱导出唯一的原因：“觉得热(张三)”.接下来，根据后2条规则我们可以进一步推测出：要么现在天气热、要么张三刚刚运动完、要么此二者均成立.可以看到，诱导推理是一种已知一般规则(因果关系)，从具体事实(关于某个对象的观测事实)中推演出其他具体事实(发生在该对象身上的特殊原因)的过程.

遗憾的是，ILP的目标并不是获得关于某个概念的具体事实，而是学习由一般规则组成的FOL规则集H.因此，上述FOL诱导推理不能被直接用于ILP.为此，Inoue等人[49]提出了元诱导(meta-level abduction)方法，试图使用二阶逻辑诱导来进行FOL归纳.

早在2003年，Lloyd[77]就曾指出高阶逻辑(higher-order logic)语言[3]或许能更有效地形式化并解决FOL归纳问题.二阶逻辑(second-order logic, SOL)即是一种高阶逻辑，它可以对FOL中的谓词和函数进行量化，因此对于SOL公式来说，FOL公式只是它的具体个例.比如对于SOL规则：

P(X,Y)←Q(X,Z)∧R(Z,Y).

其中,P,Q和R均为SOL变量，可被替换为任意二元FOL谓词.若将它们全部替换为“更好”，便可得到关于“更好”关系的递归FOL规则.元诱导学习试图将SOL规则作为背景知识B、将训练样例E作为观测到的具体事实来进行诱导推理，最终得到的便是具体的SOL规则集合，即FOL规则集H.

不过，元诱导学习并未实现真正意义上的SOL诱导.它需要将描述原始概念的FOL谓词转化为逻辑常量，并将背景知识中的SOL规则转化为FOL规则，以将SOL诱导表示为FOL中的诱导问题进行求解.最终还需将诱导得出的具体事实进行还原，才能获得待求解的FOL规则集H.

Muggleton等人[50]提出的元解释学习(meta-interpretive learning, MIL)在逻辑程序中实现了一个可以解释SOL规则的元解释器(meta-interpreter)，真正实现了SOL诱导推理.MIL允许用户在B中定义一组被称为“元规则”(metarule)的SOL公式BMR，并通过元解释器来对这些元规则进行SOL中的诱导推理.

MIL的目标可以这样描述：给定背景知识B、训练样例E和SOL元规则BMR，MIL需要找到一种SOL变量替换θ将元规则的SOL变量替换为关于原始概念的FOL谓词，以得到FOL规则(集)BMRθ，使得BMRθ∪BE.换言之，MIL通过令H=BMRθ将式(1)中对H的搜索转化为对θ的搜索.

这种搜索是通过SOL中的诱导推理完成的，而诱导推理中的已观测事实是“E可证”.因此MIL需要在对E的证明过程中诱导出θ的取值.以表2的任务为例，待证明的样例为“E=更好(瓜2,瓜3)”，设此时BMR只包含一条元规则R≡P(X,Y)←Q(X,Y).证明过程开始时，MIL会将R的规则头与E进行合一，以表示E是可证明的结论，为此需采用变量替换：

θ1={P=更好,X=瓜2,Y=瓜3},

将其应用于BMR中的元规则R，得到:

Rθ1=(更好(瓜2,瓜3)←Q(瓜2,瓜3)).

为了令证明成立，必须保证该规则体中的“Q(瓜2,瓜3)”赋值为true.通过对表2中的事实进行查询，可看出只需使用变量替换:

θ2={Q=色泽更黑}

即可令B∪Rθ1θ2E成立.保留θ1中的SOL变量替换可得{P=更好}，最终令即可得到一个候选假设模型

Rθ=(更好(X,Y)←色泽更黑(X,Y)).

显然，MIL可看作一种以SOL元规则为模板进行的FOL规则搜索.

由于SOL变量能被替换为任意FOL谓词，MIL的规则搜索比基于FOL归纳运算的ILP更加灵活：当元规则头和规则体中的SOL变量被替换为相同谓词时，便形成了递归规则；当元规则头被替换为B中不存在的谓词时，便实现了谓词发明.

例如文献[50]以楼梯的3D点云作为训练样例，学会了关于楼梯概念的模型假设：

staircase(X)←s1(X).

staircase([X,Y,Z|Planes])←

s1([X,Y,Z])∧staircase([Z|Planes]).

s1([X,Y,Z])←vertical(X,Z)∧horizontal(Z,Y).

其中，(X,Z)，(Z,Y)和Planes均为点云中的平面；{X,Y,Z}为平面的边界；谓词vertical和horizontal分别表示平面的方向为垂直和水平，谓词staircase(X)表示平面序列X是一段楼梯.该模型中第2条规则即为递归规则，而s1则是被发明的谓词.经过解读可知s1代表“一级台阶”，而第2条规则表示“楼梯加上一级台阶依然是楼梯”.

显然，MIL的假设空间结构依赖于元规则的选取.若仅使用“P(X,Y)←Q(X,Y)”作为元规则，那么MIL将永远无法学会形式为P(X,Y)←Q(X,Z)∧R(Z,Y)的FOL规则.此外，由于MIL的诱导过程中可以使用BMR中的任意一条元规则作为模板，元规则的总数会影响MIL的搜索效率.Cropper与Muggleton[78-79]研究了元规则选择对MIL假设空间完备性的影响，证明BMR只需包含2条元规则，其假设空间即可包含所有通用图灵机可计算函数.但对于一般的目标概念H*，MIL通过这2条元规则学得的模型H′只能保证在语义上与H*等价.而在形式上，H′所包含的规则条数可能比H*多很多，这往往要求MIL在对样例的证明过程中增加搜索深度.因此仅仅减少元规则条数不一定能够提高MIL的学习效率.

3.2 概率扩展

3.2.1 概率逻辑程序

经典FOL只能用于形式化“非真即假”的推理过程.为了在FOL中引入概率分布，需要对原始的FOL语义进行扩展——即允许逻辑事实依概率为真.那么式(2)的学习问题可以重写为

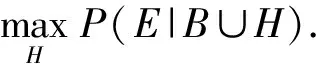
(4)

式(4)不再要求H与训练样例E绝对一致，仅要求H尽可能在对E赋值的判断上少犯错误.

为了适应模型语义的变化，还需对式(1)中FOL规则的语法进行扩展.一般可以采用如下形式的概率逻辑规则(probabilistic logic rules)：

p∷A←B1∧B2∧…∧Bn.

(5)

其中，p∈[0,1]为概率值.当n=0时，式(5)退化为一个概率原子公式(probabilistic atom)p∷A，当A不含变量时它被称为概率事实(probabilistic facts)，它表示A是一个随机变量，且A服从参数为p的二项分布.

由概率FOL规则构成的逻辑程序被称为概率逻辑程序[32]，为了使用概率逻辑程序进行推理，必须严格定义其上的概率分布形式.

FOL系统的语义由领域内所有具体事实的赋值决定，因此最直接的方法便是将概率分布定义在这些具体事实上，这种定义方式被称为“分布语义”(distribution semantics)[34].它将领域中所有具体事实作为随机变量，并在其上定义联合概率分布.考虑图2中的PLP模型：

0.8∷根蒂更蜷(瓜1,瓜2).
0.3∷敲声更闷(瓜1,瓜2).
0.6∷色泽更黑(瓜1,瓜2).
false←根蒂更蜷(X,Y)∧根蒂更蜷(Y,X).
false←敲声更闷(X,Y)∧敲声更闷(Y,X).
false←色泽更黑(X,Y)∧色泽更黑(Y,X).
更好(X,Y)←根蒂更蜷(X,Y)∧敲声更闷(X,Y).
更好(X,Y)←敲声更闷(X,Y)∧色泽更黑(X,Y).

Fig. 2 An example of probabilistic logic program
图2 概率逻辑程序示例

其中行1～3定义了3个带权的具体事实，它们是该领域中分布的来源；其他几行为一般的FOL规则.

若将PLP中所有FOL规则构成集合记为R，所有概率事实的集合记为F.假设F中的概率事实相互独立，W∈F是所有赋值为true的概率事实，那么W出现的概率为

(6)

例如，若W仅包含图2中的前2个概率事实，那么它出现的概率为PF(W)=0.8×0.3×(1-0.6)=0.096.W加上原有的FOL规则集R即可得到一个普通的一阶逻辑程序：

根蒂更蜷(瓜1,瓜2).
敲声更闷(瓜1,瓜2).
false←根蒂更蜷(X,Y)∧根蒂更蜷(Y,X).
false←敲声更闷(X,Y)∧敲声更闷(Y,X).
false←色泽更黑(X,Y)∧色泽更黑(Y,X).
更好(X,Y)←根蒂更蜷(X,Y)∧敲声更闷(X,Y).
更好(X,Y)←敲声更闷(X,Y)∧色泽更黑(X,Y).

根据W不同取值而产生的所有一阶逻辑程序被称为“可能世界”(possible worlds)[80].在每个可能世界的内部都可进行正常的FOL推理.如此便可以计算PLP中任意原子公式A为真的概率：

(7)

式(7)表示原子公式A为真的概率等于所有蕴涵A的可能世界的概率之和.以图2为例，除去互斥事实后该领域的可能世界共有8个，其概率分布如表4所示.通过计算可知，“更好(瓜1,瓜2)”为真的概率是0.144+0.096+0.036+0.024=0.3.

Table 4 Possible Worlds of the PLP in Fig.2表4 PLP(图2)的可能世界与概率分布

早期的PLP语法不允许FOL规则像式(5)那样拥有自己的权重，实际上，使用概率事实(布尔随机变量)加FOL规则的PLP的表达能力已经足够强大，能够直观地定义基于布尔随机变量的贝叶斯网、马尔可夫链和隐马尔可夫模型等常见概率模型.

Dantsin[32]在提出PLP时便确定了“概率事实加FOL公式”的基础语法规则，但由于其语法过于灵活，在PLP上进行精确概率推断比较困难.为此，Poole[33]对PLP语法进行了简化，并证明贝叶斯网是这种PLP的一个特例.Muggleton[37]提出的随机逻辑程序(stochastic logic programs)在PLP中引入了递归规则，能够通过采样来进行概率推断.由于不断递归产生的具体事实概率值呈指数级减小，因此SLP的概率推断可以保证有界.随后Poole[38]和Vennekens[40]在PLP中引入了带权规则，进一步扩展了PLP的语法，使其有能力表达多值概率分布.

De Raedt等人提出的ProbLog[41]是现在应用最广泛的PLP系统.它集成了许多成熟的PLP语法，并进一步优化了PLP概率推断的效率.它通过将PLP编译为二元决策图(binary decision diagrams, BDD)[81]来将PLP的概率推断转化为一种可满足性(SAT)问题，然后使用带权模型计数(weighted model counting, WMC)来实现高效的PLP推理.最新的版本ProbLog2[82]将基于BDD的WMC改进为基于d-DNNF(deterministic decomposable nega-tion normal form)[83]的WMC，进一步提高了推理效率.

近年来，针对不同的应用领域，研究者们依旧不断地提出新的PLP系统.例如与贝叶斯网相结合的CLP(BN)[39]、与ASP(answer set programming)相结合的P-Log[42]、与因果推断相结合的CP-logic[43]、为信息检索设计的PROPPR[55]等.它们大多仍使用分布语义对PLP进行建模，仅在做概率推断时有一定区别.有兴趣的读者可参阅相关文献[46,84].

3.2.2 概率归纳逻辑程序

概率归纳逻辑程序(PILP)[46]是以PLP为模型的机器学习方法，其任务为找到满足式(4)的假设模型H.为便于讨论，令其中的H=(Γ;Θ)，这里的Γ表示假设模型中的FOL规则结构，Θ代表所有概率规则和事实的参数.在无歧义的情况下，可以省略式中的背景知识B，将式(4)重写为

(8)

虽然PILP使用的数据形式上还是逻辑事实构成的集合，但由于引入了概率分布，其本质是关于随机变量的采样.因此PILP中的样例一般被写为D={E1=e1,E2=e2,…,EM=eM}，其中的Em表示第m次采样的随机变量(具体事实)集合，em表示本次采样的结果，即Em中所有具体事实的赋值.为了能够用D来对模型进行估计，一般假设这些采样结果服从独立同分布.于是，式(8)中的后验概率可以写成：

(9)

PILP学习的目标即为最大化似然函数L(Γ,Θ|D)=P(D|Γ,Θ).通常采用对数似然函数，那么PILP最终被形式化为

(10)

若Γ已知，则PILP退化为参数估计问题：

(11)

其中，PΓ是结构为Γ的概率逻辑模型的分布函数，对基于分布语义的PLP，PΓ就是式(7)中的P.

当Em为模型中所有随机变量——即领域中全部具体事实时，PILP的参数学习问题可以直接使用极大似然估计[1]解决.例如Cussens[45]提出的FAM(failure-adjusted maximization)和ProbLog[41]使用的LFI-ProbLog[51]等.

然而在大部分应用中，训练数据仅包含模型中一部分具体事实的赋值.这种情况相当于参数估计时存在隐变量.记模型第i组样例中的隐变量为Xi，则式(11)的目标可以重写为

(12)

当Γ未知时，PILP需要同时学习规则结构和模型参数，大部分算法选择交替地对它们进行学习.

De Raedt等人[46]提出的PLP模型压缩方法试图通过贪心算法来逐条删除PLP中的规则，并确保每次删除规则后得到的PLP关于训练数据集的似然值最大.该方法虽能对PLP模型结构进行修改，但难以从数据中学习新规则.

Bellodi和Riguzzi[54]提出的SLIPCASE通过ILP的规则精化[18]来生成候选Γ，并采用EMBLEM[53]算法来学习模型参数.Bellodi和Riguzzi[58]提出的SLIPCOVER算法则通过演化计算来改进SLIPCASE中基于规则精化的结构搜索，可有效地缩小搜索空间.

戴望州和周志华[56]提出的SUL(statistical unfolded learning)试图将ILP中的命题化[68]方法扩展至PILP.它首先将训练数据表示为一个超图，然后通过关系型路径查找[85]来构建关系型特征并对数据集进行命题化.接下来，SUL采用统计模型在命题化后的数据集上进行学习，最终将模型转化为概率逻辑规则集.与其他PILP方法相比，SUL能够以较高的效率同时学习规则结构与参数.此外，SUL还实现了PILP中的谓词发明.

3.3 可微构件嵌入

在决策树等模型中嵌入神经网络这样的可微构件早有研究[86].在ILP中嵌入可微构件的策略目前有2种：1)使用线性运算和神经网络来替代逻辑运算，并对FOL系统中的真值进行连续放松；2)将规则结构搜索中的组合优化转换为参数空间中的连续优化.与ILP和PILP相比，可微构件的嵌入进一步提升了学习效率，并允许模型拥有更大的数据吞吐量.

Rocktäschel与Riedel[65]提出的neural theorem prover(NTP)方法采用了第1种策略.它保留了逻辑程序中的后向链(backward chaining)推理，并使用神经网络来代替推理中用到合一等运算.后向链是逻辑程序中一种对原子公式进行证明的方式，MIL[50]的元解释器便借鉴了其思想.对于一条FOL规则a(X,Y)←b(X,Y)∧c(X,Y)，当用户查询目标概念具体事实a(1,2)的赋值时，它会首先被用来与规则头a(1,2)进行合一，得到变量替换θ={X=1,Y=2}；再将规则体中的原子经过θ替换可得b(1,2)∧c(1,2).后向链递归地证明这2个原子，若它们均为true，那么对该规则的证明成功，得到a(1,2)的赋值为true.

NTP将证明过程中使用的合一运算转变为神经网络unifyσ(A,B,S)=S′，其中A与B为待合一的2个原子，每个原子p(e1,e2,…,em)被表示为一个k(m+1)维向量(σ(p),σ(e1),…,σ(em))，其中σ(X)表示符号X的嵌入形式，k是其长度；S与S′分别为合一之前与之后的证明状态，它包含一个集合Sφ和一个标量Sψ∈[0,1].前者用于存储目前为止所有使用过的变量替换θ，后者代表目前状态下合一成功的可能性.σ为NTP网络的所有参数，它包含所有逻辑符号(谓词及常量)的嵌入以及所有unifyσ(A,B,S)网络的参数.A与B的合一可能涉及到多种情况，NTP分别对它们进行了定义.例如若A=e1和B=e2均为逻辑常量时，则unifyσ会直接输出其嵌入的相似度；若A是变量时，则B被直接赋值为σ(A).

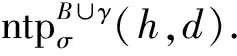
Evans和Grefenstette[66]提出的∂ILP则主要采用了第2种策略.它首先将所有可能的候选假设模型提前构建出来；然后为每个候选模型设置一个权重；最终根据训练样例对权重进行优化，筛选出权重最高的模型作为输出.

为了限制候选模型的数量，∂ILP规定对每个目标概念p只能学习一个由2条FOL规则组成的假设模型，其中每条FOL规则都依照一条SOL元规则[50]为模板而生成.它将式(2)中的ILP学习目标改写为优化问题：

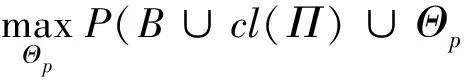
(13)

为了求解该目标，∂ILP也采用策略1将FOL中的赋值放松为[0,1]区间内的连续值，并定义关于Θp的负对数似然函数：

其中e和y分别为训练样例及其标记；P(e|Θp,Π,B,T)表示当(Θp,Π,B)确定时，经过T步演绎后e赋值为true的可能性.

为了优化该目标函数，∂ILP需要将p(e|Θp,Π,B,T)中的FOL演算转化为连续可微的函数运算.它将候选假设模型中的每条FOL公式R转化为一个可微函数FR:[0,1]n|→[0,1]n，这里的n为领域中所有具体事实的个数，因此FR的定义域和值域均为领域中全体具体事实的赋值.

x[a]=max(Fj(a[i]),Fk(a[i])).

∂ILP虽然是一种可微分模型，但它几乎完全保留了FOL规则的形式.与PLP的分布语义类似，它的FOL语义直接建立在领域中全体具体逻辑事实的赋值上.在许多不带噪声的ILP任务中，∂ILP的学习效果甚至可以与MIL[50]相媲美；而当数据中存在噪声时，它依然能够学到有效的FOL规则.其局限在于假设模型的形式不够灵活.当目标概念难以仅用2条规则描述时，用户必须将其分解为2个甚至更多待学习谓词，并为它们一一设定元规则作为模板.此外，∂ILP在进行参数学习之前必须枚举所有的候选模型，并将其全部用于FOL推理.事实上，绝大部分候选模型可能是无效、甚至矛盾的，因此∂ILP可能将大量计算资源浪费在无效模型的推断中.

一方面，嵌入可微构件的ILP能够有效地利用GPU等并行计算设备，在一些仅需简单逻辑推理的关系型学习任务中实现高效学习；但另一方面，它们加入了大量约束来对ILP模型的形式进行简化，无法保证待学习的目标概念仍然存在于假设空间中.

4 应 用

ILP在早期一般被应用于生物、化学和制药等领域.Golem曾被应用到蛋白质结构预测[27]任务中，并取得了比神经网络更好的效果；Progol被应用于生物医药研究上，并辅助科学家们发现了重要的生物诱变剂[29]；基于诱导推理的ILP则被用于学习生物的新陈代谢规律[88].

除了经典ILP系统之外，PILP也在许多任务中得到应用.例如，自然语言是一种结构性强但形式很灵活的数据.PILP既可以有效地引入语法等背景知识，又能从概率上对其不确定性进行建模，因此已被应用于自然语言处理[60].

ILP也影响了其他机器学习领域的研究.例如在统计关系学习(statistical relational learning， SRL)[89]中，ILP常被用于对SRL模型结构进行初始化[90].而在概率图模型中，ProbLog可以作为一种效率非常高的概率推断引擎来对图模型上的推理和学习进行加速[41].

得益于FOL语言强大的表达能力，ILP能用于辅助科学发现.例如生态学中的一个重要问题是从生物数量的变化判断物种之间的捕食关系.因为收集到的数据量十分庞大，若由科学家来对它们一一进行检验则需要消耗很长时间.并且物种间的捕食关系可能十分复杂，一个物种的数量往往受十几种其他物种的影响.生态学家们拥有大量复杂的领域知识，能通过FOL语言进行表达.Bohan等人[91]将MIL应用于该问题，不仅实现了数据驱动的食物网自动构建，还通过MIL自动发明的谓词，辅助科学家们发现了许多新的现象.

由于ILP学得的模型具有良好的解释性，用户可以更好地加以利用.例如Progol曾被应用于一个叫“机器人科学家”(robot scientist)的项目中.每当ILP从实验数据中学得一个模型，生物学家们便对它发现的FOL规则进行深入分析，然后根据这些分析结果来设计新的实验.这种模式将人类的科学发现与机器学习组成一个闭环：人类知识被用于设计科学实验；实验结果最终成为机器学习的数据来源；从数据中学得的模型最终被用于更新人类的知识并设计下一步实验.该计划运用这种模式成功发现了带有重要功能的基因片段[30-31].

上述应用中所使用的均为关系型数据.而Muggleton等人[92-93]提出的Logical Vision则试图将ILP直接应用于像素表示的图像数据以进行视觉概念学习.该方法用其他学习模型来探测图像中分隔主物件与背景的“边界点”，同时结合FOL表达的几何概念作为背景知识，通过ILP学习更复杂的视觉概念.Logical Vision采用了认知科学中的“假设-检验”模型，试图在符号表示的抽象概念学习与原始数据感知之间架起桥梁.借助领域知识，Logical Vision甚至可以学会预测未出现在图像中的物体[92].例如，基于简单的光学常识，该方法仅从一幅图片中即可学会判断图像外光源的位置.更有趣的是，得益于FOL强大的表达能力，Logical Vision在光源学习任务中得到的FOL规则还能够从图像中解读出关于反射面凹凸形状的歧义，并通过对不同光源位置进行假设来解释这种歧义.这在目前其他形式的机器学习中很难实现.

5 讨论与展望

与其他类型的机器学习技术相比，ILP有其自身的优势.

1) 使用FOL作为表达语言的ILP拥有强大的表达能力和推理能力，便于对复杂结构的领域知识进行处理和利用.

2) FOL规则有良好的可理解性.每条FOL规则均遵循“若X成立，则Y成立”这样的简单模式，且其中的谓词、函数符号大多取自于背景知识中的原始概念，所以学得的模型有良好的语义.

3) FOL规则有着良好的可重用性.由于背景知识和假设模型均为FOL规则集，ILP学得的模型可以作为背景知识被直接应用在其他ILP任务中.例如，戴望州等人[93]提出的Logical Vision便将学习“三角形”概念所得到的FOL规则集作为背景知识重用于“直角三角形”的概念学习任务中.依照这种模式，ILP可以实现从简单到复杂任务的分阶段学习[94]，并不断将学得的模型进行重用，这为实现“学件”[95]等构想提供了便利.

但另一方面，ILP技术本身还存在很多局限，很多问题有待解决.

1) 由于FOL规则的形式和结构是离散的，其假设空间十分复杂.为了提高学习效率，PILP与可微构件的嵌入在一定程度上对FOL模型的语义和语法做出了放松.但是，对FOL语义的放松导致难以区别错误规则和领域噪声造成的规则冲突，甚至无法保证放松后的假设空间仍包含目标概念.此外，机器学习任务不仅面临着日益增长的数据量，还面临着越来越庞大的领域知识.例如，WordNet[96]作为自然语言处理中最常用的领域知识库之一，它拥有的词汇量与二元具体事实的数量已分别超过150 000条与200 000个.现有的ILP方法很难对如此庞大的背景知识加以利用.

2) 目前的ILP不能进行非单调学习.只能不断地学习与背景知识不发生冲突的新规则.这使得它们十分依赖于背景知识的正确性，然而现实机器学习任务中往往很难确保背景知识的正确性.

3) 几乎所有的ILP方法都只能从逻辑符号表示的数据中进行学习[97].但现实机器学习任务中往往涉及到很多非符号类型数据，例如像素构成的图像、波形组成的音频等.此外，ILP任务中的原始概念及具体事实通常需由领域专家从原始数据中标注而来，这往往需要消耗大量成本.

对上述问题目前已经有一些探索.例如，在工程上可以尝试采用分布式计算来提高ILP的搜索效率[98].而在理论上，限制ILP效率的瓶颈主要在于FOL对模型完备性和一致性的要求.对这2个要求该如何放松，放松至何种程度，放松的过程中如何保证学习的效率，均是值得解决的问题.

对非单调学习问题，一种可行的方式是为ILP引入非单调推理模型，例如信念修正中的AGM模型[99]等.对于PILP来说，该问题则更加复杂，由于它允许数据集中出现噪声，学习系统还必须能够区分由数据噪声和错误规则导致的冲突.

对如何从原始数据中自动抽取符号表示，在ILP中嵌入可微构件是一种探索，例如Evans和Grefenstette[66]提出的∂ILP即可接入预训练的卷积神经网络，从手写数字图像中学习大小与关系.戴望州等人[100]提出的诱导学习(abductive learning)则将FOL诱导推理与深度学习相结合，实现了逻辑模型和深度学习模型的同时训练.其他机制尚有待探索.

此外，ILP良好的可理解性或可对其他形式的机器学习方法产生一定启发.目前在该方向中的探索可大致分为2类:1)将ILP作为独立的部件与其他机器学习方法相结合；2)将ILP所使用的FOL演算嵌入机器学习过程.例如，戴望州和周志华[101]采用第1种策略，试图通过诱导推理来约束统计机器学习.Socher等人[102]提出的NTN(neural tensor network)以及Cohen[103]提出的TensorLog则采用第2种策略，将FOL演算表示为张量运算嵌入深度神经网络.第1种策略有助于保持FOL的表达能力，但是将FOL演算与机器学习分离为2个相对独立的过程；第2种策略便于引入“端到端学习”，但是一定程度上损失了FOL的表达能力.

总的来看，作为一个已经发展了30年的机器学习分支方向，ILP已经取得了很多的进展和成果.尤其在人们对机器学习的可理解性愈来愈关注的今天，ILP的研究可能值得更多研究者关注和参与.