智能芯片的评述和展望

韩 栋 周聖元 支 天 陈云霁 陈天石,3

1(中国科学院计算技术研究所智能处理器中心 北京 100190)2(中国科学院大学 北京 100049)3(上海寒武纪信息科技有限公司 上海 201203)

人工智能是研究如何让计算机从原始数据获取知识，实现类似人类的行为或智能的学科.人类作为地球上拥有最高智慧的生物，有着区别于传统计算机的感知、学习和决策等能力.近些年，人工智能技术在许多商业领域的应用取得了巨大的成功.人工智能技术使得电脑能够像人类一样，在复杂多变的真实环境中做出判断和决策.其中发展最为迅速的技术是模仿人类大脑神经系统结构的人工神经网络(ANN).人工神经网络的基本单元是感知器，它可以接受一系列输入然后产生输出.多层的感知器组成一个层级性的网络结构，每层网络中的感知器接受上层的输入，然后生成输出传递给下一层，最终产生输出.

人工神经网络的概念最早由McCulloch和Pitts[1]在1943年提出，并且他们提出了第1个神经网络模型，即神经元模型(M-P)模型.之后，基于神经突触模型，Knott[2]在1951年提出了第1个神经网络学习策略.1958年，Rosenblatt[3]发明了用来进行模式识别的感知器模型，并且证明了在监督学习的策略下感知器模型可以收敛.1974年，Werbos[4]发明了著名的监督学习算法——反向传播算法(BP)，这大大推动了神经网络的发展.

近年来，随着世界各地科研人员和科技公司的重视和投入，人工智能的研究取得重大进展，在语音识别、图像分类、自然语言处理、系统辨识与控制、医疗诊断等应用领域取得了巨大突破[5-17].

传统的人工智能算法运行于CPU或GPU之上，但随着人工智能算法中人工神经网络的网络结构迅速膨胀，单一的CPU或GPU在人工智能的处理上十分低效，于是很多硬件研究人员也开始转向能够有效支持人工智能算法的性能更强大的领域专用处理器的研究及多核处理器系统的研究.

但是，随着半导体工艺达到纳米级的尺度，栅氧化层泄漏损耗在整个芯片能量消耗中占据更大的比重，而且沟道掺杂浓度提高会导致结泄漏损耗增加[18].所以，能量密度的增加使得保证所有晶体管在全频率和额定电压下同时开关动作，并且保持芯片工作在安全温度范围内变得十分困难.

此外，Esmaeilzadeh等人[19]的研究表明，在给定温度和能量的要求下，8 nm的集成电路中需保持断电的元件(dark silicon)的比例会达到50%～80%，系统仅仅能在最好的情况下获得7.9倍的加速.在这种情况下，研究人员开始研究专用的协处理器和通用处理器组成的混合系统来提高系统的性能.

1 人工智能简介

1.1 经典算法

本节主要讲述SVM算法[20]、k-Means算法[21]以及感知器算法[3]等经典人工智能算法.

SVM算法[20]是一种通过线性和非线性变换，对二分类问题进行有监督学习的算法.其首先通过核函数，将支持向量映射到高维度空间，然后在高维度空间依据范式进行线性分类，最终得到分类超平面.然后其通过已有的核函数以及该超平面对后续测试集进行分类.

k-Means算法[21]是一种通过迭代将数据进行无监督学习的聚类算法.其首先任选k个数据作为聚类中心，然后对每个数据点计算其与聚类中心的距离，再后重新计算聚类中心，最后判定用以评测数据的测度函数是否收敛，如果收敛则结束，否则继续调整聚类中心.

感知器算法是一种针对二分类问题的监督学习算法.其通过权重和输入进行内积，得到激活值，然后依据激活值与数据标定结果，对权重进行更新，从而逐渐收敛得到二分类权重.

1.2 人工神经网络基本算法

近几年，人工智能算法中的人工神经网络算法所占比重日益加大.传统的神经网络使用Sigmoid函数作为神经元的激活函数，使用BP算法作为训练方法.但BP算法由于其残差会从靠后一个层向前一层反馈的时候，乘以因子得到前一层的残差，因此，如果因子总是小于1，会产生“梯度消失”现象.随着网络层数的加深，“梯度消失”的现象更加严重，优化函数容易陷入局部最优解，并且局部最优更可能偏离全局最优，深层网络的效果可能还不如浅层网络.深度神经网络(DNN)[22]使用ReLU函数代替了Sigmoid函数，从而有效克服梯度消失的问题.最初，DNN中采用全连接层进行连接，但是因为网络输入层的节点很多，同时全连接层要求下层神经元和上层所有神经元形成连接，这样一来网络的参数数量会迅速膨胀.但是，实际上，在很多应用中，譬如图像领域，只有图像中局部的像素之间才存在关联，所以下层网络只需要和上层网络中的局部生成连接即可.卷积神经网络(CNN)就是基于这种思想，通过卷积核将下层和上层进行连接，卷积核参数在上层节点中共享，从而减少了网络的参数.卷积神经网络主要包括卷积层、汇聚层、归一化层和全连接层(分类层)这4种网络层.

1) 卷积层.卷积层通过几个滤波器(核)提取输入数据的特征.假设卷积层的输入尺寸为xi×yi×di，每一个卷积核的尺寸为Kx×Ky，步长为Sx,Sy.则输出特征图(a,b)处的值为

其中，f(*)一般为激活函数，如ReLU函数;wi,j,k和β代表相应的权重和偏置.

2) 汇聚层(池化层).汇聚层的主要作用是降低特征图的尺寸，进一步减少网络中的参数数量，同时减少过拟合的出现.汇聚层常用最大值函数或平均值函数作为滤波器的形式，保留局部的最大值或平均值.设窗的大小为Kx×Ky,最大值的情况表示为

3) 归一化层.归一化层通过不同特征图的相同位置值的对比来模拟生物神经元的横向抑制机制.归一化层有2种类型，局部对比归一化(LCN)(即将每个数据与同一特征层相邻位置的数据进行归一化)和局部响应归一化 (LRN)(即每个数据与不同特征层的同一位置的数据进行归一化).实际使用中，LRN由于其跨越特征层做归一化的特性，因而使用较多.LRN形式为

其中，α,β,k是该层的参数，M参数是特征图fi的邻居个数.

4) 分类层(全连接层).分类层通常作为神经网络的末层，输出节点与输入层全连接，可计算为

其中，f(*)是最大值函数或其他激活函数;w和β代表相应的偏置.

1.3 常见人工智能应用算法

1.3.1 AlexNet

AlexNet[23]是一个8层的卷积神经网络，在ImageNet LSVRC-2010比赛对120万图像的1 000分类问题中，它达到了top-1 37.5%,top-5 17.0%的错误率，并且该模型的变种在ILSVRC-2012比赛中获得了冠军.

AlexNet的前5层是卷积层(某些卷积层中含有池化层)，后3层是全连接层，最后一层是一个1 000维的softmax层.它有4个新的特征：

1) 使用ReLU非线性激活函数.采用了非线性的激活函数ReLU，比传统使用Sigmoid的等价网络快6倍.

2) 多GPU训练.120万张图片训练时的计算量太大，因此将它们的网络分布在了2个GPU上.它们在每个GPU上放置一半的神经元，同时只在某些特定的层上进行GPU之间的通信.

3) 局部响应归一化.即引入了LRN，从而增加了模型的泛化能力.

4) 重叠池化.传统的CNN中采用局部池化层，即池化单元互不重叠，亦即步长s等于窗的边长z.在该网络中采用了s=2，z=3的池化层，即重叠池化.

AlexNet针对过拟合采取了2种方法：1)数据增强.该网络中采用2种数据增强的举措.一是进行图像变换和水平翻转，从256×256的图像中提取5个(四角及中心)224×224的图像块并进行水平翻转，最终得到10个图像，对这10个图像在softmax层的结果进行平均.2)失活(dropout).失活是指以0.5的概率把隐层神经元的输出设为0，这样来强迫神经元学习更鲁棒的特征.在测试时使用所有神经元，但将它们的输出乘以0.5.该网络的前2个全连接层使用了失活方法.

1.3.2 GoogLeNet

GoogLeNet[24]是一个22层的深度卷积神经网络，基于Inception架构[25]，该架构能够在保持计算量不变的基础上增加网络深度和广度.GoogLeNet在ILSVRC2014比赛中取得了当时的最好结果.

提高深度 CNN性能最直接的方式是增加其深度和广度.然而这种方式使得系统更容易过拟合，同时也增加了计算资源的消耗.解决该问题的基本方法是将全连接层替换为稀疏的全连接层或卷积层.然而在非均匀的稀疏结构上进行数值运算时，现行的计算架构效率低下.

Inception架构基于的主要思想是：使用容易获得的稠密子结构近似覆盖卷积神经网络的最优稀疏结构.据此产生了图1所示的结构：使用不同尺度的卷积核进行卷积，提取更加丰富的特征，然后进行聚合.

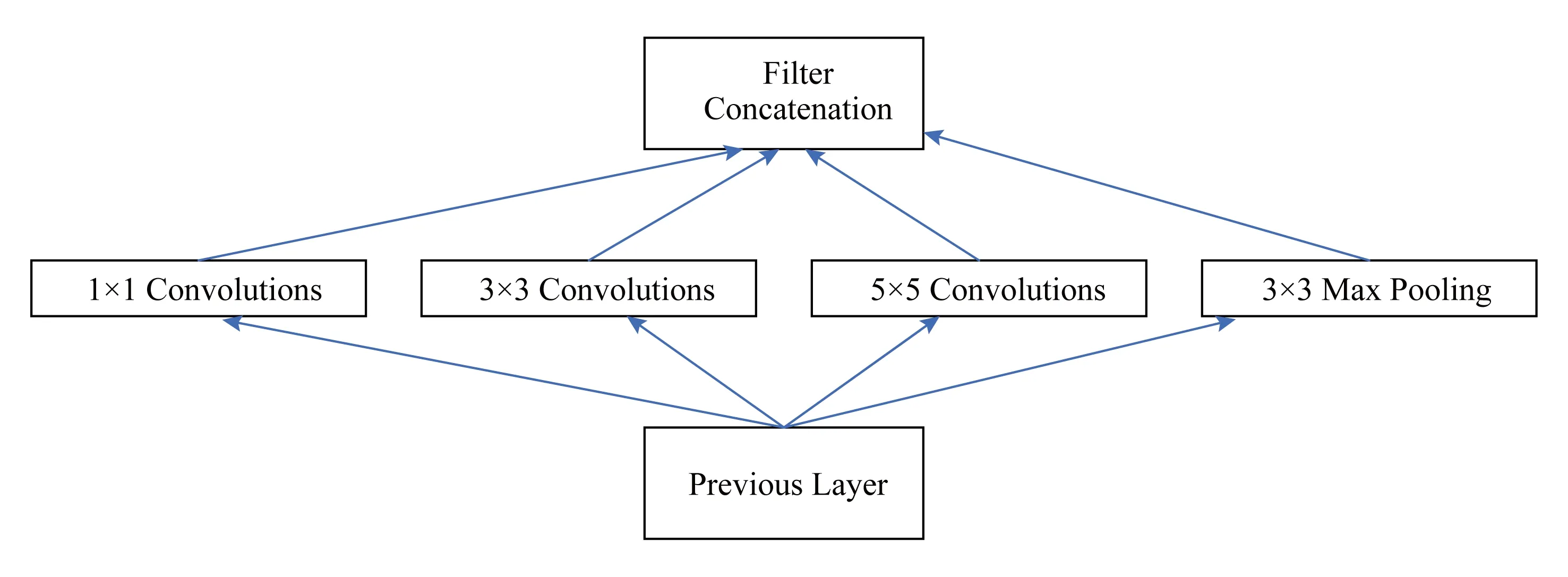
Fig. 1 Initial architecture of Inception network图1 初始Inception结构

Inception架构基于的另外一个思想是：在计算要求高的地方减少维度.图1中所示的的卷积核仍然会带来很大计算量，于是使用了的卷积核降维之后再进行卷积.如图2所示:

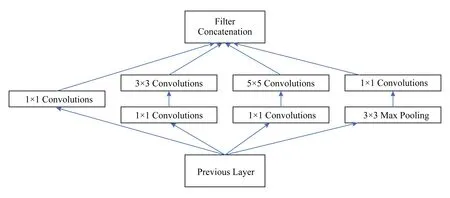
Fig. 2 Final architecture of Inception network图2 最终Inception结构

1.3.3 ResNet

ResNet[26]基于残差学习框架，拥有更深的网络结构，但复杂度仍然较低.该网络在ImageNet测试集上取得了3.57%的错误率，并且在ILSVRC2015分类任务中赢得了第1名.

在解决梯度消失的基础上，一方面较深的模型效果更好，另一方面随着深度的增加准确率会发生饱和，然后迅速下降.这种退化不是由于过拟合引起的，增加层数会带来更大的误差.ResNet通过引入深度残差学习框架，解决了退化问题.

ResNet中的思路是：

1) 残差学习.如图3所示，假设多层网络可以近似复杂函数H(x)，这等价于让网络近似残差函数F(x)=H(x)-x，然后加入前馈得到H(x)=F(x)+x.

2) 快捷恒等映射.多层网络可以表示为y=F(x,Wi)+x，如果F,x维度不匹配，可以使用Ws来匹配维度y=F(x,Wi)+Wsx.

3) 网络结构.先设计简单网络，设计原则为：相同输出特征图尺寸的层具有相同数量的滤波器；特征图尺寸减半时将滤波器数量加倍.然后在简单网络基础上加入快捷连接.

Fig. 3 Residual network图3 残差学习网路

1.3.4 Faster R-CNN

先进的目标检测算法依靠区域提议算法(region proposal algorithm)和基于区域的卷积神经网络(R-CNN).其中Fast R-CNN利用很深的网络实现了接近实时的速率，而提议算法(proposals)是计算的主要瓶颈.R-CNN使用GPU进行运算，将区域提议算法在GPU上实现是一个加速的方法，但这样就不能进行共享计算.为此，Faster R-CNN[27]引入了区域提议网络(RPN)，代替了以前使用的选择性搜索(selective search)或滑动窗口算法进行区域提议.RPN与检测网络共用全图像的卷积特征，实现了几乎零成本的区域提议过程.

RPN的思路是:基于共享卷积层所得的特征图对可能的候选框进行判别.RPN引入锚点(anchor)机制，对特征图进行卷积相当于使用滑窗在特征图上进行平移，在特征图的每个位置可以预测多个提议区域(假设有k个)，每个位置可以在滑窗的基础上加入尺度和长宽比，例如在文献[27]中定义3种尺度和3种长宽比，则k=9，这样的每个候选窗口称为一个锚点，对于W×H的特征图有W×H×k个锚点.之后的网络产生2个分支，一个分支用于计算目标边框的坐标和宽高(边框回归层reg)，一个分支用于判断边框确定的区域是不是目标(分类层cls).

为了训练RPN，给每个锚点按照4个规则标定类别标签(是或不是目标)：1)如果候选框与真实框交并比(IoU)最大，标记为正样本；2)如果候选框与真实框交并比IoU>0.7，标记为正样本；3)IoU<0.3标记为负样本；4)其余情况对训练目标没有帮助.然后根据Fast R-CNN的多任务损失方法最小化目标函数，损失函数为

为了能够让RPN和Fast R-CNN共享卷积层，有3种方法：1)交替训练.先训练RPN，然后用提议训练Fast R-CNN，Fast R-CNN微调的网络用于初始化RPN.2)近似联合训练.每次BP迭代时，前向过程生成区域提议，反向传播过程中，对共享层组合RPN损失信号和Fast R-CNN损失信号，其中忽略了提议边界框的导数，故为近似联合训练.3)非近似联合训练.加入了使边界框坐标可微分的ROI(region of interesting)池化层.

1.3.5 GAN

生成对抗网络(GAN)[28]同时训练一个获取数据分布的生成网络G和一个用来判断样本是否属于训练集的识别网络D，这是一个对抗的过程.训练的目标是，使G最大化让D出错的可能.这是一个极小化极大值(minimax)问题，训练的结果是G生成近似训练集的数据分布，而D判断样本属于任何一方的概率都是1/2.在G和D都是多层感知器(MLP)的情况下可以使用BP算法进行训练.

2 人工智能处理器

2.1 FPGA

FPGA的可编程性和可重构性等特点允许在短时间内对定制的设计进行评估，以此缩短开发周期，节省设计的开发费用.因此，有很多研究人员基于FPGA平台进行人工智能处理器的研究和实现.

Farabet等人[29]实现了一个类RISC(精简指令集计算机)的可编程卷积网络处理器.该处理器通过多个DSP并行地计算使用相同的输入的不同输出的局部和，然后平移输入(窗口)来完成相应输出的卷积.Farabet等人[30]后来在Xilinx Virtex 6 FPGA平台上实现了一个可扩展数据流硬件结构.该系统包括多个计算单元(tiles)，每个计算单元集成了多个一维卷积器(MAC)来构成二维卷积器.

由于二维卷积广泛应用于图像处理等场景中，Cardells-Tormo等人[31]提出了用于二维卷积的基于FPGA的结构.这种结构需要相对更少的片上内存开销，因此可以用低成本的FPGA实现.此外，他们还提出了单位面积最大吞吐量准则，用来说明这种结构的高效性.

之后，随着任务复杂度日益增加，因此，为了能处理越来越复杂的多层感知器，Ordoez-Cardenas等人[32]使用低成本的Xilinx Spartan-3E FPGA实现了多层感知器神经网络(MLP)和相应的学习算法.他们设计了一个模块化的方案，使系统能够灵活地调整到特定的应用中.同时，流水线结构也提高了这个系统的性能.

在处理神经网络系统的过程中，由于计算量增大，因此，功耗问题日益严峻，Maashri等人[33]发明了一个用于通用识别的神经网络系统.该系统基于一个用于视觉处理的仿生神经网络模型HMAX，相比于CPU和GPU，它能够分别达到7.6倍和4.3倍的加速，节省12.8倍和7.7倍的能量消耗.

Gokhale等人[34]设计的nn-X则是一个可扩展、低功耗、用于加速深度神经网络的协处理器，它能够达到理论227Gops/s和实际200Gops/s的性能，同时整个系统的功耗只有8W.在Xilinx ZC706平台上实现的内核使用2个ARM Cortex-A9 CPU作为主处理器，主处理器用来解析神经网络并将其翻译为相应的指令，然后将数据传递给协处理器nn-X.

随着研究的推进，脉动型结构突显出其在执行卷积运算中的优势.SCoNN[35]是一个用于CNN推理阶段的脉动型(systolic)硬件实现.它通过多个2D数组处理单元和一个滑窗实现并行的卷积处理.为了节省更多的能量和带宽，SCoNN[36-37]直接把中间结果储存到RAM中来作为下层的输入数据.Sankaradas等人提出了由systolic并行卷积基元和一个数据传输专用控制器组成的协处理器，它拥有用于协处理器的片下高带宽内存，同时使用较低的数据精度，在每次内存操作时使用打包过的数据字.该协处理器在FPGA中实现，需要和主机一起工作.但是，脉动阵列机具有很多优缺点.其优点有：可以大量复用输出数据；更简单的处理单元设计；为并发性调整的流水线；对计算密集型问题有相对较高的性能；简单数据流和常规控制；具有可扩展性和模块化特性.缺点有：对不同规模人工智能算法的灵活性不足；存在内存带宽约束等[38-39].

随着人工智能算法的数据量越来越大，通常需要使用额外的储存空间来储存它们.同时，随着人工智能算法越来越复杂，带宽需求越来越大.因此，研究者们开始寻找新的结构来充分地重利用(reuse)人工智能算法中的数据.

Qiu等人[40]提出了一个基于FPGA的人工智能加速器，它使用了全连接层的权重矩阵的奇异值分解来减少内存访问，同时采用动态精度数据量化方法来减少能量和逻辑消耗.他们发现卷积层的核心是计算而全连接层的核心是内存，基于此，他们使用不同的方案对待2种数据.他们利用Xilinx Zynq ZC706实现的设计在150 MHz下的CNN的运算中达到了137.0 GOP/s的性能.

Zhang等人[41]实现了基于VC707 FPGA的61.62 GFLOPS人工智能加速器.他们使用了循环分块和转化技术来定量分析卷积层的计算和带宽需求，然后借助roofline模型开发了一个统一的结构.

Suda等人[42]则更深入地进行了Zhang等人的研究.他们不仅关注卷积层的加速，还提出了一种系统的设计开发方法，来最大化基于OpenCL的FPGA加速器的性能.

为了减少额外的内存和带宽开销，Peemen等人[43]提出新型的人工智能加速器.他们设计了一种灵活的内存管理方式，用来支持数据访问和优化人工智能算法中的数据位置.这种加速器能够最小化片上内存需求，同时能够最大化数据的利用率，因此这种方法避免了不必要的封装(footprint)和能量消耗.

此外，除去将人工神经网络部署于FPGA，Rice等人[44]基于George和Hawkins[45]研究的理论结构，实现了基于FPGA的分层贝叶斯网络模型.结果表明相比于全部在Cray XD1运行的软件，他们的硬件提升了75倍的平均吞吐量.Kim等人[46]提出了一种生成高效置信网络(deep belief nets)原型，该模型比在高档CPU上最优的软件实现快了25～30倍.

2.2 ASIC

专用集成电路(ASIC)是一类专用的电路，能够给设计者实现应用最大程度的自由.为了满足不同消费者的需求，ASIC常常有更小的体积、更低的功耗、更高的性能、更强的安全性和量产之后更低的成本.

卷积运算在人工智能算法中占据很大的运算量，它本质上适合做并行运算.早期关于专用人工智能芯片的研究主要关注如何尽可能快速地实现卷积运算，以满足实时处理的需求.

Lee和 Aggarwal[47]提出了一种并行的二维卷积结构，这种处理器拥有和图片像素数目相同的处理单元，这些处理单元之间网状相连，它可以使用任意大小的2维或3维的卷积核.Kamp等人[48]提出了一种全集成的2维滤波器(卷积核)宏单元(macrocell)，它提供了7×7的可编程的卷积核，但只适用于垂直对称的参数掩模.

Kim等人[49]提出了一种201.4 GOPS的实时多目标识别处理器.芯片模仿人类视觉系统，在含有3级流水线的神经感知器中使用了仿生神经网络和模糊电路.

由于人工智能算法中的Deep CNN在许多计算机视觉任务中能够达到最高的准确率，在经济的推动下出现了很多Deep CNN加速器.Sim等人[50]提出了一种Deep CNN加速器，它拥有1.42 TOPS/W的能量效率.为了减少能量消耗，他们应用了一个双范围的乘法累加器(DRMAC)来进行低能耗的卷积运算.他们利用了分块排列的方式(tiled manner)，使用和片上存储相同大小的数据块和压缩的卷积核进行卷积运算，来减少片下内存的开销和带宽需求.

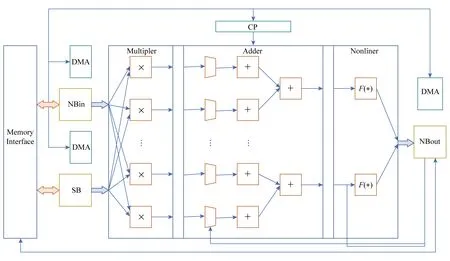
Fig. 4 Architecture of DianNao图4 DianNao结构方框图

此外，还有利用人工智能算法内在错误弹性(intrinsic error resilience)的硬件加速器研究.Hashmi等人[51]提出了一种仿生的计算模型，并且揭示了相对皮质网络(relative cortical networks)的内在容错性.这个模型的关键是使用固定型方案(stuck-at)来保护函数计算结果，当硬件出现错误时不做任何处理.人工智能算法本质上能够抵抗短暂或者永久的错误，基于此，Temam[52]提出并且实现了一个能够忍受多重错误的人工智能芯片.它可以使用多种的基于ANN的算法，实现一些高性能任务的运算.它和其他定制芯片一样，相比通用芯片能够提高2个数量级的能量效率.

3 DianNao系列加速器

3.1 DianNao

DianNao[53]作为DianNao系列中最早的加速器，其计算峰值达到452 GOP/s，在台积电65 nm的工艺下，面积为3.02 mm，功耗为485 mW.DianNao主要关注内存使用的加速,其利用陈天石等研究者提出的启发式模型方法，达到了计算量和内存体系之间完美的平衡,从而获得了相比CPU具有3个量级的能量效率提升.同时，尽管GPU在运算速度上超过了DianNao，但它需要的能量和面积是DianNao的100倍.

DianNao基本结构为一个控制逻辑(CP)和其控制一个输入缓冲区(NBin)，以及另一个缓冲区(SB)和其将输入神经元和权重传递给的神经功能单元(NFU)，然后还包括输出缓冲区(NBout)，其从NFU接收输出神经元，如图4所示.其中使用了一个内存接口来为3个缓冲区中的数据流进行路由.其NFU利用交错的3级流水线结构，将不同类型的层在DianNao中被分解为2个阶段或者3个阶段，并且在CP的控制下进行流水线运算，同时对多个输出神经元进行计算.

为了在降低计算的能量消耗的同时，优化数据传输策略，减少数据传输的能量，DianNao将片上存储被分为3部分：输入缓冲区(NBin)、输出缓冲区(NBout)和突触(权值)缓冲区(SB).其收益如下：1)可以调整SRAM为合适的读写带宽，而不必是同等的带宽.由于权重的数目大约比输入神经元和输出神经元的数目高一个量级，这种专用的结构可以为读请求提供更好的能量和时间性能.2)分离储存和神经网络位置先验信息，使得DianNao能够避免数据冲突，这种发生在缓冲区的冲突往往需要消耗时间和能量来弥补.3)DianNao能够让NBin缓冲区工作在循环缓存状态，来重用输入神经元数据.因此，DianNao相比CPU或GPU将数据传输带宽减少到1/30～1/10.

3.2 DaDianNao

DaDianNao[54]是在DianNao的基础之上构建的多核处理器，其处理器核心的规模扩大到16个，同时增大了片上内存.DaDianNao基于28 nm工艺，运行频率为606 MHz，同时其面积只有67.7 mm2，功率只有大约16 W.DaDianNao不仅支持推理算法，同时支持训练算法，以及权值预训练环节(RBM).

Fig. 5 Architecture of DaDianNao图5 DaDianNao结构方框图

为了有效避免逻辑和数据的拥塞，DaDianNao采用如图5所示的分块(tile-based)结构，即将所有输出神经元的运算被分为16个片段，分给相应的运算块(tile).其每个运算块(tile)同时处理16个输出节点对应的输入节点，即单个芯片同时进行256个并行运算.

DaDianNao一方面使用了大量分布式的eDRAM来使所有的突触(权重)靠近运算器，另一方面通过采用了一个高带宽的胖树(fat tree)结构来向每个块(tile)广播相同的输入数据以及收集每个块中不同的输出节点值.其在胖树结构的末端，有2个eDRAM起到和DianNao中的NBin和NBout相同的作用.同时，中心eDRAM中的输入神经元值被广播到所有的块(tile)来计算不同的输出，这些输出被集中到另一个中心eDRAM.这样，一方面，在MLP和卷积层中，比起神经元，权重的数量更多，所以移动神经元值比移动权重更合理；另一方面，靠近计算单元储存权重提供低能耗/低延时的数据供应.同时中心eDRAM连接到了hyper transport(HT)2.0接口，用以和相同的芯片通信系列.

3.3 PuDianNao

PuDianNao[55]是DianNao系列中，用以支持多种人工智能算法的人工智能芯片.其支持的算法有k-近邻、朴素贝叶斯、k-均值、线性回归、支持向量机、深度神经网络、分类树等.PuDianNao在1 GHz的频率下，具有每秒1.056万亿次运算的峰值性能，但是只有0.596 W的功耗和3.51 mm2的芯片面积.多种人工智能算法在PuDianNao上运行的平均性能相当于使用通用GPU的性能，但是其能量消耗只有GPU大约百分之一.

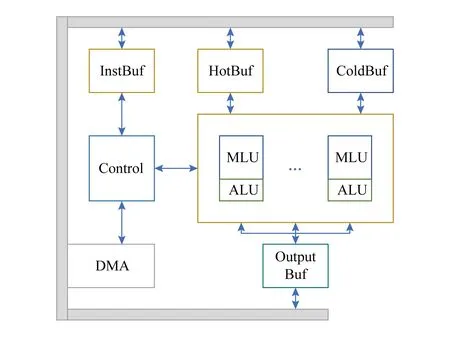
Fig. 6 Architecture of PuDianNao图6 PuDianNao结构方框图

如图6所示，PuDianNao由功能单元、数据缓存、1个控制模块、1个指令缓存和1个DMA组成.其中，为了支持多种人工智能算法，功能单元被分为1个用来支持多种基础运算的机器学习功能单元(MLU)和1个辅助MLU的算法逻辑单元(ALU).

MLU包含6级流水，用以支持多种人工智能算法.1)第1级计数级(Counter)通过按位与运算或比较输入数据然后累加结果来加速计数运算，计数运算在分类树和朴素贝叶斯中经常使用.2)第2级加法级(Adder)用来计算机器学习中普通的向量加法.3)第3级乘法级(Mult)计算向量乘法，并且可以从前一级或数据缓存中输入数据.4)第4级加法树级(Adder tree)对乘法的结果进行求和.5)第5级累加级(Acc)对求和结果进行累加.6)最后的第6级Misc级负责排序和线性插值运算，排序器可以用来寻找累加级中的最小值，线性插值器用来计算非线性函数的近似结果.其中，乘法级、加法树级和累加级配合共同实现点乘运算.此外，ALU用以提供MLU支持的基础运算外的各种各样的运算.

片上数据缓存被分为3个分离的部分：8 KB的HotBuf，16 KB的ColdBuf 和8 KB的 OutputBuf.HotBuf用来存储短重用距离(short reuse distance)的输入数据，相反，ColdBuf用来存储长重用距离(long-reuse distance)的输入数据，而OutputBuf用来存储临时或输出数据.其一方面适应了机器学习中多种集群平均重用距离的变量，另一方面可以消除由不同读入数据位宽引起的额外带宽开销.因此，PuDianNao可以避免内存带宽成为系统瓶颈.

3.4 ShiDianNao

Fig. 7 Computation mode of ShiDianNao图7 ShiDianNao运算模式

ShiDianNao[39]是用来处理图像实时人工智能算法的人工智能芯片.它能够被嵌入到传感器中，以实现实时的图像处理.ShiDianNao可以直接从CMOS或CCD传感器直接获取输入图像，同时仅用SRAM进行了完整的CNN映射，减少DRAM对权值的访问.其相比DianNao，它大体上提升了60倍的能量效率.

ShiDianNao加速器包括1个突触权值缓存(synapse buffer, SB)、2个储存输入输出节点数据的缓存(NBin, NBout)、1个神经功能单元(neural function unit, NFU)和1个算法逻辑单元(arith-metic logic unit, ALU)，1个用来储存指令和译码的缓存和译码器.其中，NFU用来进行加、乘、比较等基础的运算，ALU专门用于激活函数的运算.

NFU包含了一组处理基元(processing element， PE)阵列.基于2维滑窗的特点，同时卷积核的大小有限，处理基元的性质为：每个基元代表一个神经元(节点)，排列在一个2维的网格拓扑结构中.它可以传输FIFO中的数据到其相邻的基元中.

以图7所示的卷积层为例，假设PE阵列的大小为2×2，卷积层卷积核的大小为3×3，步长为1×1.在计算特征图时，每个PE计算一个输出神经元(节点)，计算结束后移动到一个新的基元中.在计算的第1个周期Cycle0，所有4个PE(PE0,0,PE0,1,PE1,0,PE1,1)从SB中获取卷积核k0,0的值，从NBin中获取第1个输入节点的值(x0,0,x0,1,x1,0,x1,1)，然后PE计算输入节点和权值的乘积，把临时结果储存到寄存器中，同时从FIFO中获取输入节点值.PE1,0,PE1,1在Cycle1中从NBin读取输入节点x2,0,x2,1，在Cycle2中读取x3,0,x3,1.PE0,0,PE0,1在Cycle1中从PE1,0,PE1,1的FIFO中读取输入节点x1,0,x1,1，在Cycle2中读取x2,0,x2,1.同时，在Cycle1和Cycle2中广播卷积核值k1,0,k2,0，储存输入节点值到FIFO中.乘法运算的结果和前一次计算的结果进行累加.Cycle3～Cycle5和Cycle6～Cycle8的操作类似.PEi,0(i=0,1)从PEi,1中获取输入节点值xi,1-xi+2,1,xi,2-xi+2,2.PEi,1(i=0,1)从NBin中获取输入节点值xi,2-xi+2,2,xi,3-xi+2,3.同时系统顺序地从SB中读取卷积核值k0,1-k2,1和k0,2-k2,2，并将它们广播给所有的PE，乘法和累加运算仍然同之前一样.这样每个PE就完成了运算，然后将累加的和传给ALU就得到了输出的y0,0,y0,1,y1,0,y1,1.

3.5 Cambricon-X

Cambricon-X[56]是一款专门针对稀疏剪枝设计的人工智能处理器.其利用人工神经网络的稀疏性，减少运算量，同时减少功耗和面积.

其总体结构如图8所示，由Buffer Controller负责从NBin中读取数据送给PE，同时将PE的执行结果存放到NBout中，PE进行具体的运算.

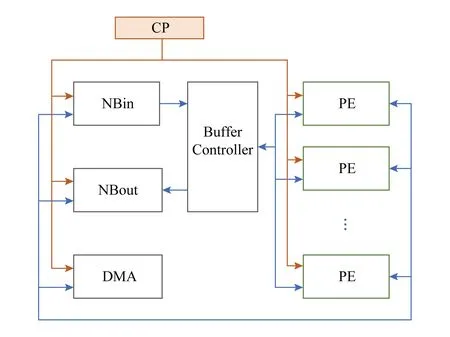
Fig. 8 Architecture of Cambricon-X图8 Cambricon-X总体结构框图

其中，Buffer Controller的结构如图9所示，同时从NBin中读取神经元，然后依据各PE中的稀疏权值对应的索引，筛选出该PE需要运算的神经元，而后将筛选后的神经元发送给相应的PE，与PE中SB存储的稀疏权值进行运算.从而，有效利用了稀疏神经网络的权值稀疏性，将不需要计算的数据在送给运算部件之前先行剔除掉.同时，其BCFU则将旁路过来的input数据和PE的运算结果进行整合，得到最终的数据，将其写入到NBout中.

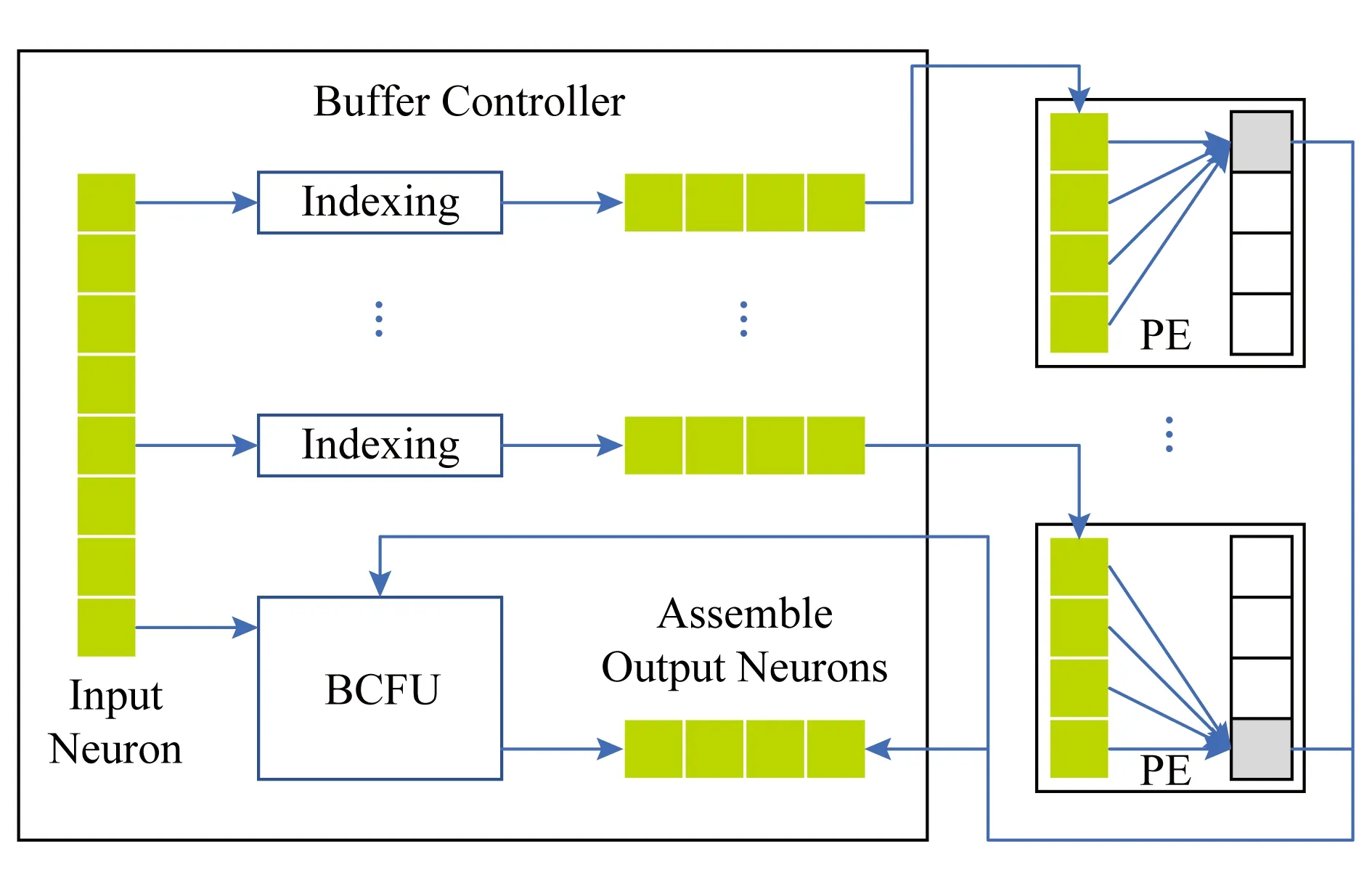
Fig. 9 Architecture of Buffer Controller图9 Buffer Controller结构框图

PE结构如图10所示，其分为PEFU以及SB.PEFU即包含乘法以及加法树，将稀疏选择之后的神经元以及权重进行乘法，然后将得到的结果通过加法树得到最终结果.SB则存放稀疏之后的权重，与稀疏选择之后的输入一一对应.

Fig. 10 Architecture of PE and PEFU图10 PE和PEFU结构框图

Cambricon-X利用稀疏选数，在16个PE的基础之上，做到了544 GOP/s的峰值，但是65 nm的工艺之下面积仅有6.38 mm2，并且其功耗仅有954 mW.

3.6 指令集

Cambricon[57]是一种新型的用于人工智能芯片的指令集结构(ISA).这种装载结构基于对现有的人工智能算法复杂的分析，集成了标量、向量、矩阵、逻辑、数据传输和控制指令等.基于10种有代表性的NN技术对指令集进行的评估表明，Cambricon对大范围的人工智能算法有很强的表示能力，并且有比x86,MIPS和GPGPU等通用指令集更高的代码密度.比起最新最先进的人工智能芯片DaDianNao(能够适应3种神经网络)，基于Cambricon的加速器原型只带来了可以忽略不计的延时/能量/面积开销，却能够覆盖10种不同的神经网络基准.

Cambricon的设计受到RISC ISA的启发：首先，将复杂、高信息量的、描述高层次的神经网络功能块(如网络层)分解为对应低层次运算的更短的指令(如点乘)，这样就可以使用低层次的运算来集成新的高层次的功能块，这就保证了加速器有很广泛的适用范围.其次，简短的指令大大地降低了指令译码器设计和验证的复杂性.

Cambricon的装载结构只允许使用加载或储存(load/store)指令对主内存进行访问.Cambricon不使用向量寄存器，而是将数据储存在片上暂存器中.Cambricon包含了4种指令类型：计算类型、逻辑类型、控制类型、数据传输类型.尽管4种指令有效长度不同，但为了设计的简单性和内存对齐的作用，所有的指令均为64 b.

Cambricon的控制指令和数据传输指令与MIPS指令类似.Cambricon包含2条控制指令：jump和conditionalbranch.为了支持向量和矩阵运算指令，Cambricon的数据传输指令支持可变数据尺寸.

基于对GoogLeNet的定量分析，神经网络中99.992%的基础运算可以被合并为向量运算，99.791%的向量运算可以被更进一步合并为矩阵运算.因此，人工智能算法可以分解为标量、向量和矩阵运算，而Cambricon充分地利用了这一点.

1) 矩阵指令.Cambricon中含有6条矩阵指令.以MLP为例，每个全连接层进行的运算为y=f(Wx+b).其中的关键运算是Wx，这可以通过矩阵乘向量指令(matrix-mult-vector, MMV)实现.为了避免转置运算，还有VMM指令，在神经网络的权值更新中，会用到W=W+μΔW运算.因此有叉乘指令(outer-product, OP)、矩阵乘标量指令(matrix-mult-scalar, MMS)和矩阵加法(matrix-add-matrix, MAM)指令.此外Cambricon还提供了矩阵减法指令(matrix-subtract-matrix, MSM)指令用于玻尔兹曼机(RBM).

2) 向量指令.不失一般性，以Sigmoid函数为例：对于向量A，执行Sigmoid运算f(A)=eA(1+eA)，即对向量A中的每个元素进行激活操作.首先，使用向量指数指令(vector-exponential, VEXP)对向量A的每个元素求指数；其次，使用向量标量加法指令(vector-add-scalar, VAS)为上述结果向量eA的每个元素加1；最后，使用向量除法指令(vector-divide-vector, VDV)计算eA(1+eA).类似地，对于其他函数Cambricon提供相应的向量指令，如vector-mult-vector (VMV),vector-logarithm(VLOG)等.此外，Cambricon提供了向量随机数指令(random-vector, RV)，用于相关人工智能算法的实现中.

3) 逻辑指令.最好的人工智能算法中往往使用比较运算或其他逻辑运算.Cambricon中使用vector-greater-than-merge (VGTM)指令用于支持最大汇聚(max-pooling)运算.此外，Cambricon还提供了vector-greater-than (VGT), vector AND(VAND)等指令.

4) 标量指令.Cambricon仍然提供基础的单元素标量运算和标量超越函数等指令.

4 人工神经网络相关技术的发展

4.1 权值与输入量化

4.1.1 二值网络

由于人工智能芯片中乘法器最消耗能量和空间，Courbariaux等人[58]提出使用只含有-1和1的二值化权重可以将复杂的乘法累加运算替换为简单的累加运算，进而提升硬件的性能.二值化连接(BinaryConnect)方法基于2个关键点：1)累加平均大量的随机梯度需要足够的精度，但含噪声的权重(可以认为离散化是一种噪声)也同样适用于随机梯度下降法(SGD).SGD每步都很小并且含有噪声，对每个权重而言，随机梯度的求和将噪声平均掉了，因此这些累加器需要足够的精度(来计算平均).同时，研究发现随机舍入可以用来进行无偏离散化.2)变化权重噪声、失活(Dropout)和失连(DropConnect)等方法在激活值或权重中加入了噪声.但这些噪声权重实际上提供了一种正则化的方法，可以让更模型有更好的推广性(避免了过拟合).这些研究说明只有权重的期望值才需要很高的精度，噪声实际上是有好处的.

BinaryConnect方法中的权重只含有+1和-1两种情况，这样乘法累加运算就可以被加减运算取代.一种直接的二值化方法如下：

这种固定的二值化方法可以通过平均大量输入权重的离散值来补偿信息的损失.另一种更精细准确的方法是随机二值化方法：

其中,σ是Hard Sigmoid 函数：

网络的更新策略是：为了保证SGD算法正常工作，只在前向传播和后向传播时使用二值化权重，权重更新时仍使用精确的权重.

4.1.2 三值网络

Hwang等人[59]提出了一种新的人工智能算法，它只需要三值(+1，0，-1)的权重和2～3位的定点量化信号.训练算法仍使用反向传播算法重训练定点网络，但使用了一些方法进行提高精度，如通过范围和灵敏度分析进行精细信号分组(elaborate signal grouping)、同时量化权重和信号值、最优量化参数搜索和对深度神经网络的考虑.

由于对权重和信号使用不同数据类型太复杂，所以需要根据它们的范围和量化敏感度对它们分组.在每层的权重中，只有偏置值(bias)需要很高的精度(它们的范围通常比其他权重大很多).对偏置值使用较高的(如8 b)定点数类型不会带来很大的开销.隐层信号的量化敏感度都很低，但网络输入的量化敏感度十分取决于应用.一种传统的量化方法是:通过最优步长Δ直接量化训练的浮点数权重，浮点数权重可以通过先使用玻尔兹曼机(RBM)进行预训练，然后使用误差反向传播的精细调整来获得.可以通过最小化L2误差方法(类似Lloyd-Max量化)获得初始值，然后使用穷举搜索对量化步长进行微调来获得最优步长.为了减小搜索维度，可以使用贪心算法进行逐层搜索.最终Δ大约是Lloyd-Max方法结果的1.2～1.6倍.

在权重精度很低时，直接量化方法有很高的输出误差.这可以通过使用定点优化方法重训练量化的神经网络来解决.直接对量化的神经网络使用反向传播算法往往行不通，这是因为权重的更新值往往比量化的步长小很多.为了解决这个问题，该网络同时保留高精度和低精度的权重和信号.高精度的权重用于计算误差的累计和生成量化的权重，而低精度的权重用于后向传播算法的前向和后向步骤.

4.2 计算以及传输剪枝

4.2.1 稀疏CNN

Graham[60]通过研究发现，在高分辨率人工智能算法中使用单像素笔画所写的字符是一种稀疏矩阵.同时图片填充后也可以认为是稀疏的，充分利用矩阵的稀疏性可以更加高效地训练更大更深的网络.

假设手写字符是一个N×N的二值图片，非零像素数目只有O(N)，第1个隐层可以借助稀疏性计算得更快.传统卷积层使用valid模式，但不是最优的，解决方法有：1)对输入图片用零像素填充；2)在每个卷积层使用较少数目的填充，保证卷积使用full模式；3)对一组重叠的子图使用卷积网络.而稀疏性能够组合这些好的特点.

对于手写字体而言，更慢的池化操作(窗较小的池化层，网络更深)可以保留更多的空间信息，使网络具有更好的可推广性.对通常的输入而言，慢的池化层相对需要更高的计算代价，但稀疏的输入由于在网络的前几层保留了稀疏性，就只需要相对较低的能量代价.

DeepCNet(l,k)的网络结构为：l+1层卷积层，中间是l层2×2的池化层.第l卷积层的滤波器的数量是nk，第1层滤波器尺寸为3×3，后面的层的滤波器的尺寸为2×2.在DeepCNet的基础上加入network-in-network层，NiN层卷积核尺寸为1×1，在每个池化层和最后一个卷积层的后面加入NiN层，生成DeepCNiN(l,k)网络.在该网络中，采用了2种措施来使反向传播函数更加高效：首先，只对卷积层进行失活操作，对NiN层不进行操作.其次，使用了leaky修正线性单元：

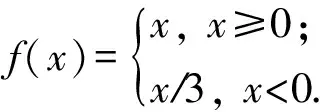
假设输入全零时，隐层变量的状态为基态(ground state)(由于偏置的存在，基态的值非零).当输入稀疏数组时，只需要计算和基态不同的隐层变量的值.为了前向传播网络，对每层计算2种矩阵：1)特征矩阵(feature matrix)是一个行向量列表，一个代表ground state，一个代表该层中每个激活位置.矩阵的宽度时每个空间位置特征的数量.2)指针矩阵(pointer matrix)是一个和卷积层大小相同的矩阵.在其中储存每个空间位置在特征矩阵中对应的行.

4.2.2 ReLU运行时剪枝

Akhlaghi等人[61]统计发现，CNN中的ReLU层的大量输出都是零值，说明了卷积层中大量的输出为负值.同时，不同中间层的零值空间分布不同.基于这个特点，SnaPEA算法能够提前判断中间计算结果是否会产生零值来决定是否提前终止，进而减少算法的计算量.SnaPEA有2种模式：1)准确模式.不会降低分类的准确率.2)预测模式.通过预测提前中止计算，以节省更多的计算量，代价是分类准确度有一定降低.

在准确模式下，将卷积核中的权重按照符号排序，正的权值在前，负的权值在后.在计算过程中定期检查求和的符号位，一旦符号位为负就终止运算，在这种情况下不会降低分类准确率.

在预测模式下，如果卷积运算在特定次数的MAC运算后低于相应的阈值，最终的结果就很可能是负的，于是提前终止运算.但是这种操作会降低最终分类的准确度，为了减小这种损失，需要确定2个参数：阈值和相应的运算次数.参数可以通过一个多变量约束的优化问题来确定，进一步通过贪心算法来解决这个问题.该算法包括3个步骤：1)独立测量准确率对每个卷积核引入不精确值(提前停止)的灵敏度，根据这个灵敏度确定每个卷积核的参数；2)联合每层各个核的参数，为每层确定一组参数；3)迭代调整各层参数，使得在减少最大计算量的同时达到可以接受的准确率.由于确定参数的算法执行一次，所以并不会在CNN执行期间增加额外的运行开销.

预测模式执行特定次数计算后根据阈值判断是否终止计算，因此需要确定计算哪一部分权值.一种方法是将权重按照绝对值降序排序，选择幅值较大的进行计算.但由于忽略了数据随机性和数据之间的依赖，这种方法会导致正确率急剧下降.SnaPEA将权重按升序排序，并将其分为几组，从每组中选取幅值最大的权重参与计算.在这种情况下，划分的组数就是运算的次数.

4.3 特殊器件

3.1节所述的DianNao系列芯片采用了分布式片上内存来减小数据传输的能量开销，此外还有其他降低数据传输能量开销的方法：例如，让片下高密度的内存更加靠近计算单元，或者直接将计算单元集成到内存中.在嵌入式系统中，还会将计算模块集成到传感器中.一些相关的研究中使用了模拟信号处理，但其有增加电路敏感性和设备非理想性的缺点，导致的结果是通常使用降低的精度进行计算.另一个问题是，DNN通常在数字域进行训练，对于模拟信号处理，DAC和ADC就还需要额外的能量消耗.

同时，除了如DaDianNao等，把DRAM集成到芯片中，还可以使用TSV技术(也称3D内存技术)将DRAM堆叠在芯片上.这种技术已经以混合立方储存器(HMC)和高带宽内存(HBM)的形式商业化了.相比二维 DRAM，三维内存(3D DRAM)的电容更小，因此能够将带宽提升一个量级，同时能够节省5倍的能量.

将处理单元集成在内存中是另一种思路[62].例如，乘法累加运算可以集成在一个SRAM数组的位元(bit cell)中.在这项研究中，使用了5位DAC将字线(WL)转换成代表特征向量的模拟电压，使用位元(bit cell)储存权重(±1)，位元电流(IBC)计算出特征向量和权重的积，位元电流之间相加来对位线(VBL)放电.比起分离进行读取和运算，这种方法节省了12倍的能量.

乘法累加运算可以直接集成在先进的非易失性储存器中(忆阻器).特别地，可以使用电阻器的电导作为权重，电压作为输入来进行乘法运算，电流是乘法的输出.加法操作可以通过将不同忆阻器的电流相加进行.这种方法的优点是，由于计算被集成在内存中，所以不用进行数据的传输，进一步节省了能量消耗.可供用作非易失性储存器的器件有：phase change memory (PCM)，resistive RAM(ReRAM)，conductive bridge RAM (CBRAM)和spin transfer torque magnetic RAM (STT-MRAM)等.该技术的缺点有：降低了计算精度、需要忍受额外的ADC/DAC开销、数组大小受连接电阻的导线数目限制、对忆阻器的编程需要消耗很大的能量等.ISAAC将DaDianNao中的eDRAM替换为忆阻器，为了解决精度不足问题，其中使用了8个二位的忆阻器来进行16 b的点乘运算.

在图像处理领域，将数据从传感器传输到内存中占据了系统能量消耗的很大的一部分.因此有一些研究试图让处理器尽可能地接近传感器.特别地，大部分研究针对的是如何将计算移动到模拟域以避免ADC的使用，进而节省能量.然而，电路的非理想性导致了模拟计算中只能使用更低的精度.有研究将矩阵乘法集成在ADC中，其中乘法的高位使用开关电容进行计算.此外，还有研究实现了模拟的累加运算，其中假设3 b权重和6 b激活值的精度是足够的，这将传感器中ADC转换次数减少到1/21.更有研究将整个卷积层的运算在模拟域实现.

除了可以将计算集成在ADC之前，将计算嵌入在传感器本身也是可行的.有研究使用了Angle Sensitive Pixels传感器来计算输入的梯度，降低了10倍的数据传输消耗.此外，由于DNN第1层的输出通常是类似梯度的特征图，这使得有可能跳过第1层的计算，进一步减少能量消耗.

5 未来工作展望

人工智能日益成为工业界和学术界极其重要的一个领域.随着人工智能算法日益复杂以及人工智能处理的数据日益增大，人工智能芯片相比GPU和CPU等传统处理器，具有越来越明显的优势.人工智能芯片可以满足在日益复杂的应用场景中，对存储性能和计算能力的巨大需求.随着技术的发展和研究的深入，人工智能芯片已经发展出了诸如DianNao系列的芯片系列，解决了很多现有的问题和应用场景.但是，目前的人工智能芯片，其访存瓶颈和计算能耗依然有很多的提升空间.其未来可能的发展方向有5个方面：

1) 随着应用场景的增多，人工智能算法日益复杂，作为人工智能芯片，保持针对人工智能算法的通用性将会是一个巨大的挑战.

2) 人工智能算法中，其计算过程具有非精确性特点，因此，使用低精度量化是减少人工智能算法的计算复杂度和开销的一种重要的手段.其不仅可以如4.1节所说，使用二值网络处理特定的算法，同时还可以寻找适用范围更加广泛、更加精准的算法.将这些算法应用在人工智能芯片之后，将极大地节省芯片功耗和面积.

3) 由于现有的人工智能算法，其搜索空间庞大无比.因此，进一步利用其稀疏性质，减少人工智能算法的计算复杂度和开销，将会使得人工智能芯片具有更低的功耗和面积.

4) 随着芯片集成度越来越高，如何在一个芯片中部署多个运算核单元，并且使得这些运算核协同工作，获得较高的加速比，也逐渐成为一个重要的发展方向.

5) 对于人工智能算法，其计算单元相对简单，因此，探索新的物理器件例如光衍射、忆阻器等来进行存储和运算，可以极大地优化人工智能芯片的功耗和算法.