非椭圆接触下地铁小半径曲线外轨全寿命侧磨发展规律

王少锋，冯青松，罗信伟，刘庆杰，雷晓燕

(1.华东交通大学 土木建筑学院，江西 南昌 330013；2.广州地铁设计研究院股份有限公司，广东 广州 510010)

地铁列车运行在小半径曲线上会造成外轨严重侧磨，大量曲线外轨因侧磨超限而报废。因此，研究地铁小半径曲线侧磨特征，掌握其发展规律，具有重要的科学意义，为钢轨养护维修提供理论指导。

由于试验设备无法准确模拟曲线轨道的侧磨，诸多研究采用现场跟踪监测的试验方法。娄平等统计了25条普速铁路曲线外轨侧磨并拟合出侧磨速率[1]；周宇[2]、颜怡翥[3]、潘建杰等[4]分别对上海、广州和北京地铁大运量小半径曲线钢轨的侧磨进行了跟踪测量。

由于受到车轨条件的限制，现场试验只能从侧磨结果上进行研究，难以分析侧磨原因及各影响因素，而利用数值仿真技术则简单易行。孙宇等基于Braghin磨耗模型分析了高速铁路钢轨磨耗[5]；肖乾等基于Zobory和Braghin磨耗模型研究了摩擦系数对高速铁路车轮磨耗的影响[6]，认为在摩擦系数大于0.2后Braghin磨耗量基本不变；侯茂锐等基于Heuman磨耗指数研究了动车所小半径曲线的侧磨情况[7]；许玉德等基于非Hertz轮轨接触及能量耗散模型预测了钢轨磨耗[8]；王璞[9]基于Specht磨耗模型，张晴[10]、刘瑶[11]、杨新文等[12]则选用Archard磨耗模型模拟了重载铁路钢轨磨耗状况。

从以上研究现状可以看出，在钢轨磨耗的仿真研究中采用的材料磨耗模型并不统一。文献[5—6]针对的高速铁路直线线路几乎不存在侧磨，文献[7]未直观得到侧磨的发展规律，文献[8—12]的研究对象是钢轨整个型面的磨耗，只分析了侧磨的初期变化(小于3 mm)，而地铁半径≤300 m曲线外轨的后期侧磨达到12 mm以上[2]，因此需要更进一步的研究。

本文建立常用的地铁车辆—轨道动力学模型，基于非椭圆接触理论计算接触点的轮轨接触状态，考虑运营中的高峰期和低峰期并设置相应的权重，进行磨耗累积，研究大运量地铁小半径曲线外轨全寿命阶段(从新轨上道至严重侧磨下道)侧磨随运营时间的发展速率及规律，并与现场跟踪测试结果进行对比。

1 侧磨预测方法

1.1 改进的Archard材料磨耗模型

一般情况下轮轨之间硬度比为1～1.2∶1[13]，属于典型的黏着磨耗，常用Holm-Archard方程计算磨耗量，为

(1)

式中：V为材料的磨耗体积，m3；k为磨耗指数；FN为法向接触力，N；l为接触体的滑动距离，m；H为维氏硬度指数，N·m-2。

从式(1)中可以看出，V与FN和l成正比，与H成反比。在摩擦系数不变的情况下，式(1)变为

V=kmWs

(2)

其中，

式中：km为修正的磨耗指数，由试验或经验值得到；Ws为滑动摩擦功，由轮轨接触得到；μ为摩擦系数。

在全滑动摩擦情况下，式(2)能够较为准确地计算出金属材料磨损量。但曲线线路上的轮轨接触状态多为蠕滑，对于接触斑内的任意一点i， 其在j方向(j=x，y；x和y分别代表横向和纵向)的切向蠕滑力Fij可表达为该点法向力F0ij与轮轨蠕滑率ξij的函数，即

Fij=f(F0ij,ξij)

此时点i处j方向上的蠕滑功Wsij为

(3)

式中：vs为蠕滑速度；t为时间。

在小蠕滑状况下，轮轨蠕滑力与轮轨蠕滑率呈线性关系(斜率为蠕滑系数)，但在大蠕滑状况下，二者呈现非线性的关系。轮轨蠕滑率在接触斑上的每一点并不一致，因此滑动距离l应为滑动速率vs的时间积分，最终的蠕滑功应是横向蠕滑功及纵向蠕滑功的累积。将接触斑内钢轨的每1个点看作1个微单元，那么该微单元处的蠕滑位移在车轮通过的一瞬间非常微小，而微单元的面积相对于磨耗也十分微小，因此可以将磨耗体积近似于该点的磨耗。

1.2 轮轨接触蠕滑状态计算模型

根据式(3)可知，钢轨在某一点的磨耗与该点处轮轨蠕滑率有很大的关系，而小半径曲线上的轮轨接触斑内任一点的轮轨蠕滑率都可能不同。文献[9—12]采用FASTSIM算法得到了椭圆型的接触斑，这种模型仅适用于轨头型面曲率过渡平滑、接触斑可视为椭圆的小磨耗工况。一旦发生较大磨耗，轮轨接触斑即为非椭圆，尤其在轮缘与轨侧接触位置处，采用FASTSIM算法得到的切向蠕滑状态与椭圆型接触斑下的误差较大。因此，本文采用非赫兹接触计算轮轨接触的法向荷载，采用Kalker完全理论计算轮轨非椭圆接触斑的切向蠕滑力。

车—轨耦合系统中的任何一个动力学参数的变化都会引起轮轨接触状态的不同，应在车—轨耦合的多体动力学模型里进行求解。建立大运量地铁常用车辆A型车和B型车的标准模型，轨道参数见表1，且施加德国高干扰不平顺谱。基于多体动力学软件计算出曲线钢轨接触斑形状及其内每一点处的蠕滑率和法向荷载。

表1 地铁车—轨多体动力学模型中的轨道参数

由于地铁客流具有高峰期以及潮汐性特点，不同载客车体其重心位置、转动惯量等参数相差较大，运行时轮轨动力学参数也不同。根据我国大运量地铁运营时间、发车间隔及经过长期观测得到的客流量特征，将荷载谱分为3类，分别为AW3(高峰期超载，权重为46%)；AW2(中峰期定载，权重为46%)；AW0(低峰期空载，权重为8%)。计算每类荷载条件下钢轨磨耗，并按照所占权重进行磨耗累积，即为钢轨磨耗加权值。

1.3 外轨侧磨预测流程

钢轨侧磨是整个钢轨型面磨耗的一部分，每个轮对经过时都会在钢轨接触斑位置每个点上产生磨耗，通过建立的车辆轨道多体动力学模型得到接触斑上每一点的蠕滑功，再根据材料磨耗模型可得到每一点的磨耗hi。设置磨耗迭代阈值为hT，当接触斑上存在某一点的最大磨耗himax达到该阈值时，更新钢轨型面进行下一步迭代。阈值越小越接近于实际情况，但时间成本会急剧增加。根据多次试验，磨耗阈值取0.08～0.15 mm时能够在节省时间成本的情况下取得较高的预测精度。本文中取磨耗阈值为0.08 mm。

基于以上步骤，建立地铁小半径曲线外轨侧磨计算流程如图1所示。

图1 地铁小半径曲线外轨侧磨计算流程图

2 小半径曲线外轨侧磨预测结果

2.1 运行A型车时的外轨侧磨规律

根据图1所示流程图计算运行A型车时小半径曲线外轨型面全寿命阶段的型面演变如图2所示。由每阶段的型面数据，可以得到小半径曲线外轨侧磨发展规律如图3所示。

由图2、图3可知，运行A型车时小半径曲线外轨的侧磨发展主要分为3个阶段。

(1)从新轨上道至运营3个月左右为阶段Ⅰ，侧磨发展速率为0，磨耗首发于轨距角部分，并急剧向轨顶和轨侧位置扩展。

(2)运营3～20个月为阶段Ⅱ，侧磨出现并呈线性发展，速率约为0.53 mm·月-1，磨耗部位继续向轨顶以及轨侧下方扩展，本阶段的后期侧磨达到9 mm左右。

(3)运营20个月之后为阶段Ⅲ，侧磨速率加快，约为1.11 mm·月-1，工作边磨耗部位基本稳定，保持在轨顶中心以下27～28 mm位置处。在阶段Ⅲ的后期(运营29个月)，侧磨达到了19 mm，根据相关规范钢轨属于重伤范围，此时应及时换轨。

(4)在外轨全寿命阶段中，侧磨平均速率约为0.66 mm·月-1，拟合度达到0.958 4。因此，可以将小半径曲线外轨的侧磨在全寿命阶段中与运营时间视为线性关系。

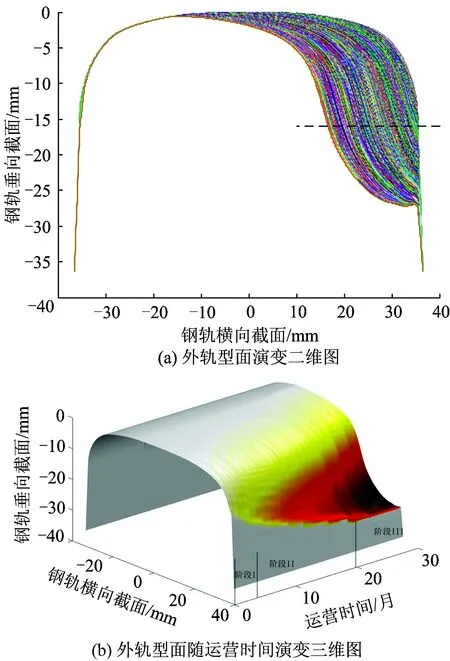
图2 运行A型车时小半径曲线外轨全寿命阶段的型面演变

图3 运行A型车时小半径曲线外轨侧磨发展规律

2.2 B型车的外轨侧磨规律

以同样的流程计算运行B型车时小半径曲线外轨型面全寿命阶段的型面演变如图4所示。根据每阶段的型面数据，可以得到小半径曲线外轨侧磨发展规律如图5所示。

图4 运行B型车时小半径曲线外轨全寿命阶段的型面演变

图5 运行B型车时小半径曲线外轨侧磨发展规律

由图4、图5可知，运行B型车时小半径曲线外轨侧磨发展也主要分为3个阶段。

(1)从新轨上道至运营5个月左右为阶段Ⅰ，侧磨速率为0，磨耗首发于轨距角部分，并急剧向轨顶和轨侧位置扩展。

(2)运营5～25个月为阶段Ⅱ，侧磨出现并呈线性发展，速率约为0.46 mm·月-1，磨耗部位继续向轨顶以及轨侧下方扩展，本阶段的后期侧磨也达到9 mm左右。

(3)运营25个月之后为阶段Ⅲ，轨侧磨耗部位基本稳定，保持在轨顶以下27～28 mm位置处。侧磨速率加快，约为1.61 mm·月-1，约3个月后又恢复到阶段Ⅱ的扩展速率。在阶段Ⅲ的后期(运营39个月)，侧磨值达到19 mm，根据相关规范钢轨属于重伤范围，此时应及时换轨。

(4)在外轨全寿命阶段中，侧磨的平均速率约为0.57 mm·月-1，拟合度达到0.946 1。因此，可以将小半径曲线外轨侧磨在钢轨全寿命阶段中与运营时间视为线性关系。

2.3 对比分析

从以上预测结果可以看出，2种车型作用下小半径曲线外轨侧磨发展具有相似的规律，磨耗均由轨距角开始，快速向轨顶和轨侧扩展。当侧磨开始产生后，呈线性发展规律，A，B型车产生的平均侧磨速率分别约为0.66和0.47 mm·月-1，比例为1.4∶1。文献[2，14]的现场监测结果表明，上海地铁某300 m半径曲线外轨侧磨平均速率约为0.47～0.59 mm·月-1，文献[15]监测结果表明，南京地铁某400 m半径曲线外轨侧磨最大速率约为0.56 mm·月-1；本文预测结果与已有现场监测结果有极大的吻合。

仿真结果表明，侧磨达到9 mm后会显著加快。文献[4]对北京地铁现场跟踪观测指出，大多数小半径曲线外轨侧磨发展到7～9 mm后，速率要明显高于前期，这也与本文预测结果十分吻合。

3 现场测试验证

3.1 侧磨发展规律的验证

为进一步研究小半径曲线外轨侧磨规律，以某特大城市大运量地铁线路为研究对象，对多条小半径曲线外轨的型面演变以及侧磨发展进行长期跟踪测试，用于验证本文预测结果的准确性。

测试结果显示，相同半径曲线即使位于同一条线路上，其侧磨发展速率离散范围较大，表明侧磨发展速率受众多因素影响。其中运行A型车时外轨侧磨速率范围为0.21～0.70 mm·月-1，最大速率与本文预测值较为接近；平均速率约为0.40 mm·月-1，最接近该平均值的曲线侧磨速率为0.44 mm·月-1，其发展规律如图6所示。从图6可以很清晰地看出，阶段Ⅰ、阶段Ⅱ以及阶段Ⅲ中侧磨发展规律的现场测试结果，都与本文的预测结果相吻合。

图6 现场测试的侧磨随时间发展图

3.2 型面演变过程的验证

侧磨发展伴随着钢轨型面的演变，选取侧磨发展过程中新轨上道、侧磨即将产生、4.7 mm侧磨、8.3 mm侧磨、11.5 mm侧磨、13.0 mm侧磨这6个阶段，对比预测型面与实测型面如图7所示。

图7 侧磨发展过程中的预测型面与实测型面

从图7可以看出：①与预测结果相同，现场实测的钢轨磨耗从轨距角部分开始，逐渐向轨顶与轨侧扩展；②每一阶段的预测型面与实测型面基本吻合，误差较大部位发生在侧磨位置以下，这是由于现场实测的钢轨在侧磨位置以下会出现肥边，由钢轨塑性流动所致。根据肥边大小，可将侧磨视为肥边的开关，即当侧磨产生时，肥边也在侧磨下方随之产生，并随侧磨的发展而增大。

当侧磨达到重伤标准即19 mm时，小半径曲线外轨的预测型面与实测型面的对比如图8所示。从图8可以看出，仿真所得到的外轨磨耗后期预测型面与实际型面十分吻合。

图8 外轨侧磨后期预测型面与实测型面的对比

4 结 论

(1)采用本文方法无论是预测侧磨发展规律还是钢轨型面演变，都与现场测试具有很高程度的吻合，能够较为精确考虑磨耗后钢轨型面的曲率变化，可对外轨全寿命阶段的侧磨进行分析研究。

(2)小半径曲线外轨侧磨发展整体上可以看成与运营时间的线性关系，但具体又可分为3个阶段，阶段Ⅰ侧磨速率为0，磨耗从轨距角开始产生并急剧向两侧扩展；阶段Ⅱ侧磨缓慢发展，速率约为0.53 mm·月-1(运行A型车时)和0.46 mm·月-1(运行B型车时)，同时肥边开始产生；阶段Ⅲ侧磨速率会明显增大，阶段Ⅱ和Ⅲ的拐点在约9 mm侧磨处。

(3)影响侧磨的因素众多，在全寿命阶段中运行A，B型车时小半径曲线外轨产生的平均侧磨速率分别约为0.66和0.47 mm·月-1。

(4)利用本方法能够以较小的成本来分析现场难以设置的参数对于外轨侧磨的影响，比如轨距加宽、轮轨润滑、轨底坡等，为减缓外轨侧磨、延长外轨使用寿命、轨道养护维修提供科学依据。