基于应力修正的土体抗剪强度影响因素分析
龚 琰,朱建群,陈浩锋
(1.成都基准方中建筑设计有限公司,四川 成都 610021;2.常州工学院土木建筑工程学院,江苏 常州 213032;3.常州市建筑科学研究院集团股份有限公司,江苏 常州 213015)
土体破坏常为剪切破坏,当土体所受剪应力超过抗剪强度时,会产生土坡滑动、地基失稳等工程问题。土的抗剪强度值受其结构状态、基质吸力及矿物成分的影响,同时与形成环境、应力历史及当前所受应力状态等密切相关,当任一因素发生变化时,土体工程性质随之改变。
众多专家学者围绕土的抗剪强度展开了理论及试验研究工作。1960年Bishop等[1]和1978年Fredlund等[2]提出了被普遍认可的非饱和土抗剪强度公式。陈正汉[3]研制的测定非饱和土强度、变形等性质的系列仪器设备,揭示了土体许多重要的力学规律。汤连生[4]从粒间吸力角度探讨其对土体强度的影响,并归纳出总吸力与抗剪强度的关系式。雷国辉等[5]通过分析已有文献,确定了宏观抗剪强度与粒间摩擦强度之间的正相关关系。曹宇春等[6]通过有效固结应力法研究了黏性土的结构性对不排水抗剪强度的影响,验证了该方法的适用性。申春妮等[7]、赵蕊等[8]分别以不同土体做试验,探讨含水量变化对土体抗剪强度造成的影响,通过拟合强度参数与含水量的关系曲线,得到变化趋势。余凯等[9]考虑剪切中面积与应力的变化对直剪试验数据进行修正,提高了数据的准确性与可靠性。诸多学者的探索,推动了学科的发展,但由于土体自身的复杂性,抗剪强度影响因素的深化研究仍然是重要课题。本文从附加应力的角度,探讨土体结构与状态被改变后,其抗剪强度指标发生的变化,以期为促进此方面的研究提供参考。
1 试验土样及方案
1.1 试样选取
试验所用土样取自江苏省常州市戚墅堰区某职业技术学校工程场地。根据各孔土层信息选取两类代表性原状土体:①粉土夹粉砂,取土深度为地表下4.0~4.5 m,青灰色,可塑状态;②淤泥质粉质黏土,取土深度为地表下7.0~7.5 m,灰黑色,流塑状态。根据《土工试验方法标准》(GB/T 50123—1999),测得土体基本物理性质指标如表1所示。
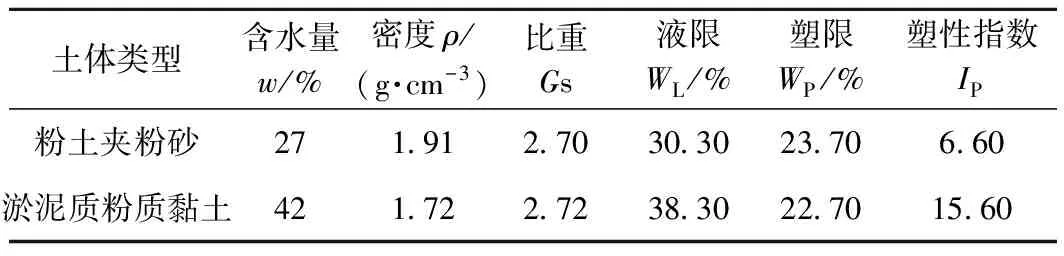
表1 土体基本物理性质指标Table 1 Basic physical property indexes of soil
将部分现场获取的土样切除表层后自然风干,碾散,过2 mm及以下标准土壤筛组,经颗分试验初步判定后取0.075 mm筛下土颗粒进行甲种密度计试验,获取其颗粒组成(图1)。由图1可知,粉土夹粉砂中<0.075 mm的土颗粒占总土质量的53.9%,其中黏粒(<5 μm)含量约为5.9%,砂粒(>0.05 mm)含量约为65%;淤泥质粉质黏土中<0.075 mm的土颗粒占总土质量的90.2%,其中黏粒(<5 μm)含量约为13.5%,砂粒(>0.05 mm)含量约为12%。
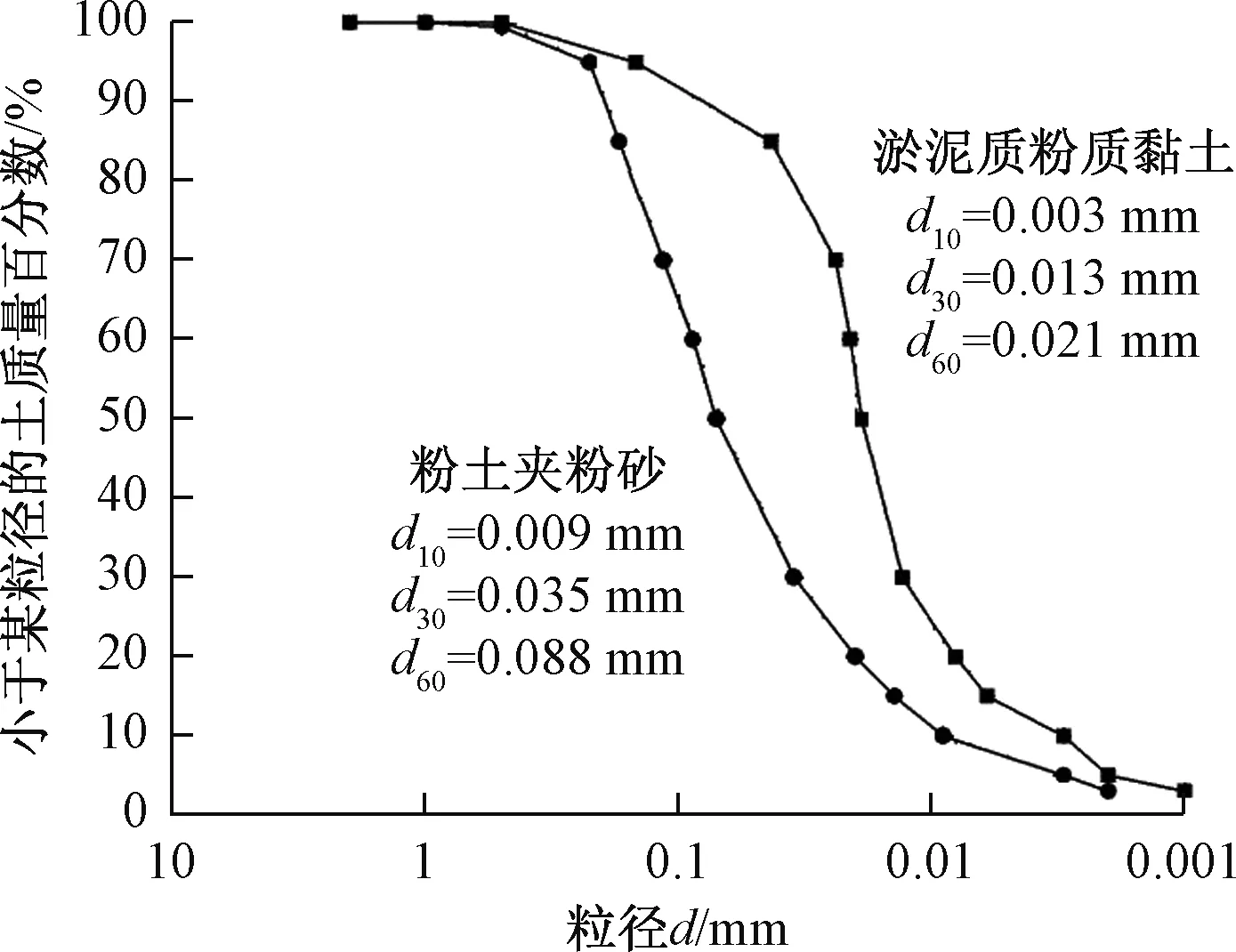
图1 试样的颗粒级配曲线Fig.1 Grain size distribution of the soil
1.2 试样制备及方案
将原状钻孔样用钢丝锯切割成约30 mm一段的圆柱体,轻缓压入环刀后用削土刀平整削成内径61.8 mm、高度20 mm的试样,随后立即用塑料薄膜包裹,防水分散失,两类土体均制样20个。
将两类备好的试样称重后各自均分成4组,依据勘探获取的土层信息及各层土土工试验物理性质指标求算待试验土体的上覆土重,在此基础上增设多组附加应力值,依次为0,100,200,400 kPa,通过GZQ系列气压全自动固结仪施行,土样经快速固结[10]后,测取其竖向变形量,同时再次称取环刀试样重,求算每组条件下各自的平均竖向变形量,挑出最为接近平均值的试样进行固结试验,测定压缩模量。剩余每组4个试样置于ZJ型应变控制式直剪仪中进行快剪试验,剪切速率控制为0.8 mm/min。
2 面积与正应力修正的直剪试验公式
两种材料共同受力,假定产生相等变形,但因自身性质的差异,会导致各材料分担力值不同,以弹性材料先做简要论述。
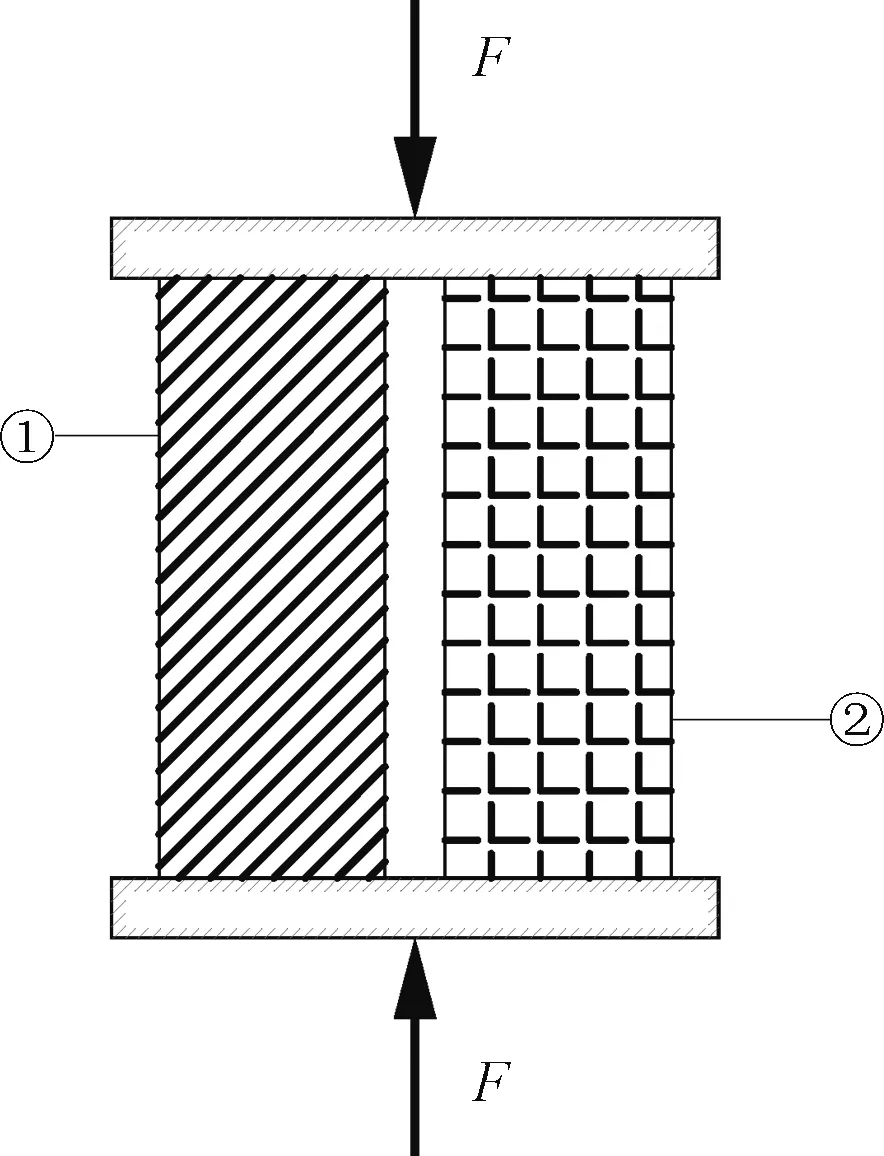
图2 模型受力示意Fig.2 Schematic diagram showing force analysis of the spring model
如图2所示,由刚度为K1的材料①和刚度为K2的材料②共同分担压力F,其各自所分担的力为F1及F2,产生的压缩变形量为λ1及λ2:
F1+F2=F
(1)
(2)
(3)
设压缩变形相等,得变形协调方程λ1=λ2。解得:
(4)
由式(4)可知,各材料所分担的力与其刚度有关,即与其尺寸及材料力学性能有关。
直剪试验仪器如图3所示,力FN通过传力板、透水石传递至剪切盒上部环刀土样后,经剪切面传至下部剪切盒与下部试样。

图3 直剪仪示意Fig.3 Schematic diagram of the direct shear apparatus
随剪切位移增大,剪切面以下压力逐步变为试验土体与铜盒共同承担(图4)。因材料刚度不同,铜盒与土体所受应力有差异。
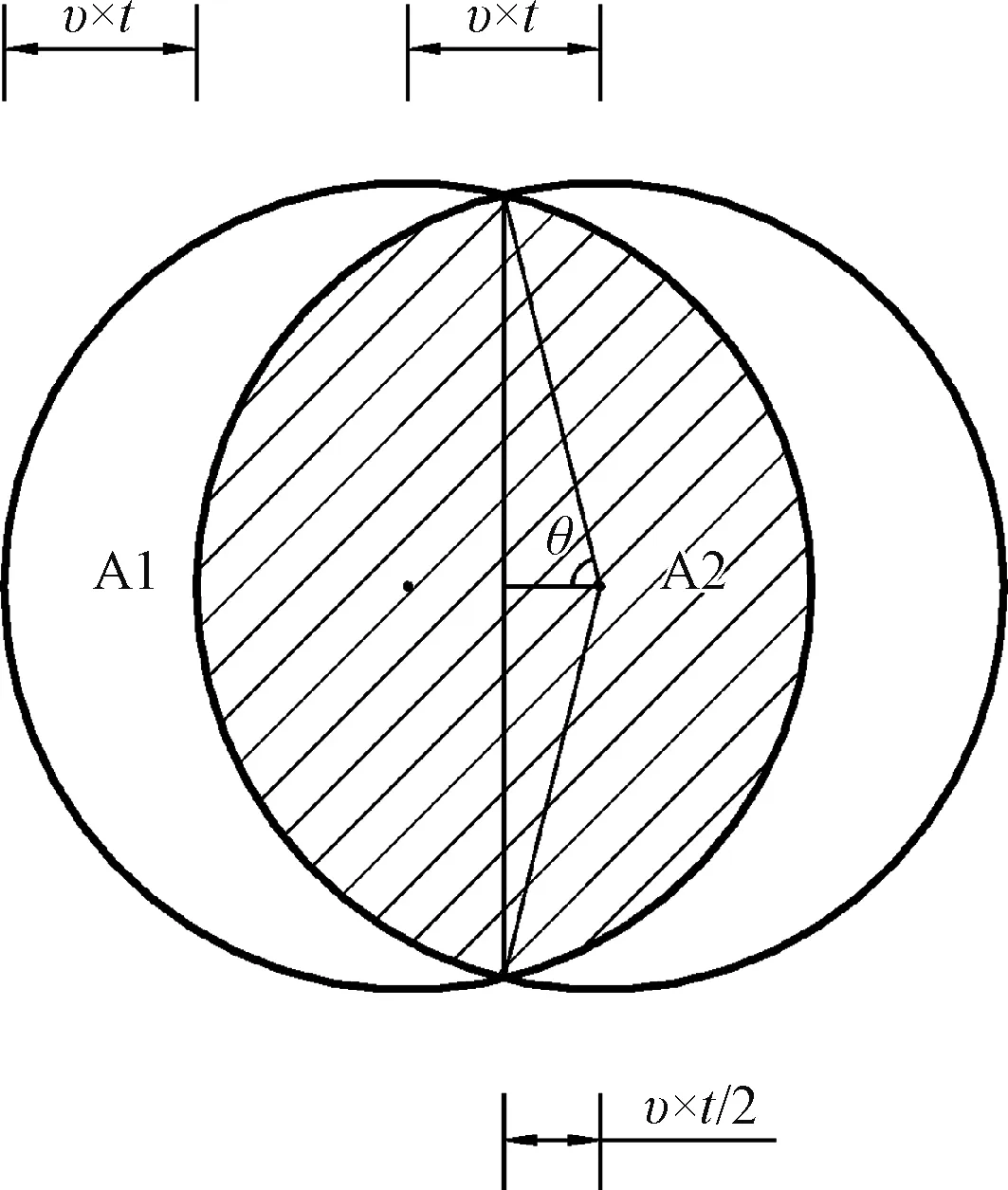
图4 剪切过程示意图Fig.4 Sketch of force analysis during the shearing process
试验中的剪应力依据牛顿第二定律所求,即:
T-τA=ma
(5)
在应变控制式直剪仪中,加速度a=0,则有:
T=τA
(6)
直剪仪中剪应力的计算公式为:
τ=CR
(7)
式中:C——量力环系数/(kPa/0.01 mm);
R——百分表读数/0.01 mm。
根据库伦定律,抗剪强度表达式为:
τf=c+σtanφ
(8)
2.1 剪切面积的修正
剪切面积A是与时间t及速度v有关的函数,面积呈现动态变化,随剪切进行不断减小。具体推导为:
(9)
(10)
剪切过程中实际剪切面积A2为:
(11)
2.2 正应力的修正
对正应力修正作如下基本假设:(1)剪切面平直;(2)材料为均匀体;(3)考虑土间竖向剪应力,忽略土体与铜盒间的竖向剪应力;(4)连续剪切过程可分解为单个状态,土体产生塑性变形,铜盒产生弹性变形,以产生峰值强度时试件状态建立受力分析模型。
剪切范围内受力及变形如图5所示,试样沉降变形如图6所示。试样按剪切面划分为上下两部分,根据上覆土体表面整体沉降量相等(考虑土间剪应力忽略土与铜盒间剪应力),得如下关系:
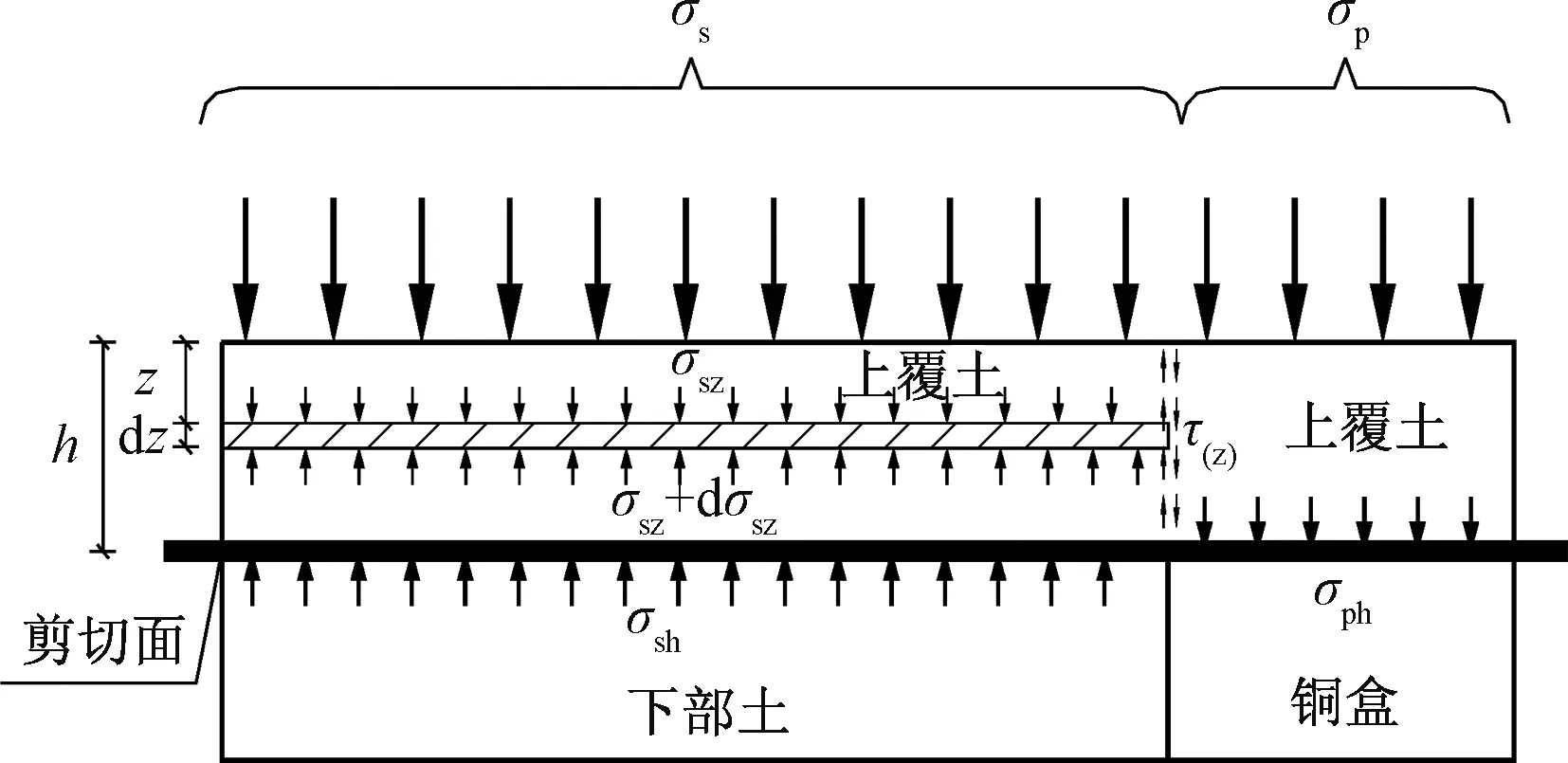
图5 剪切范围内试样受力分析Fig.5 Sample force analysis within the shear scope
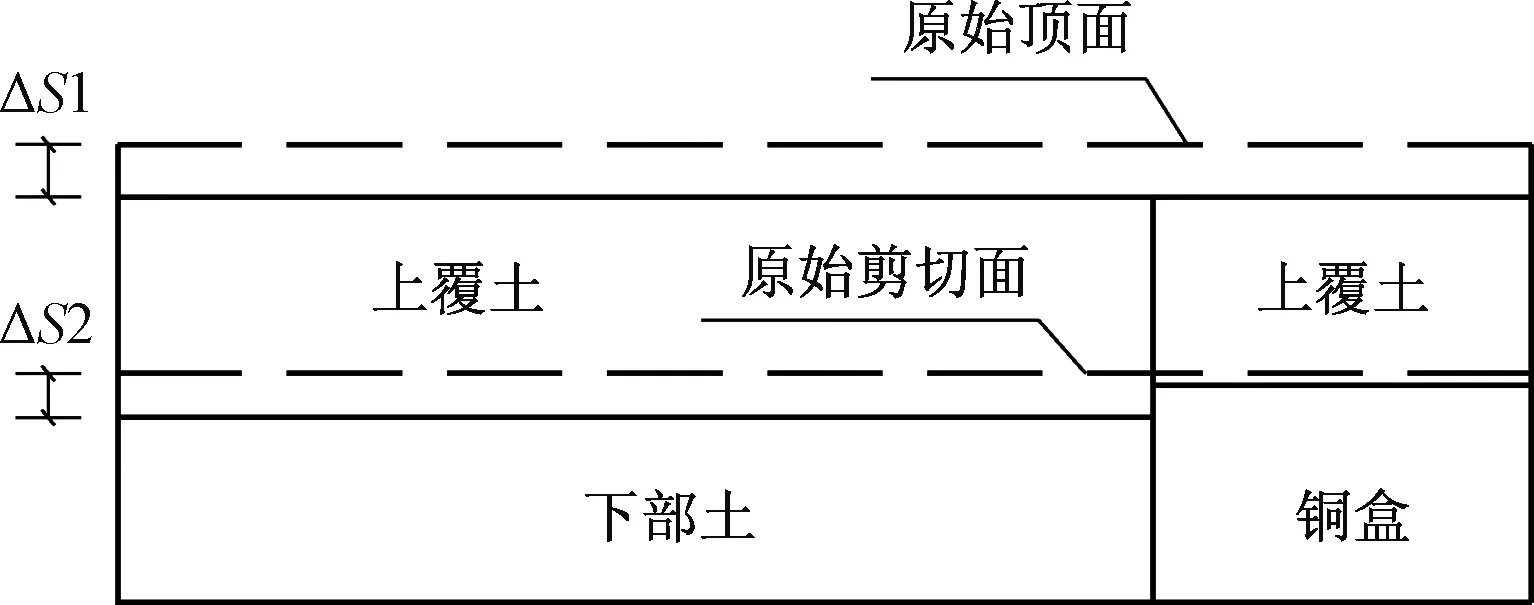
图6 试样沉降变形示意Fig.6 Schematic diagram of the sample settlement
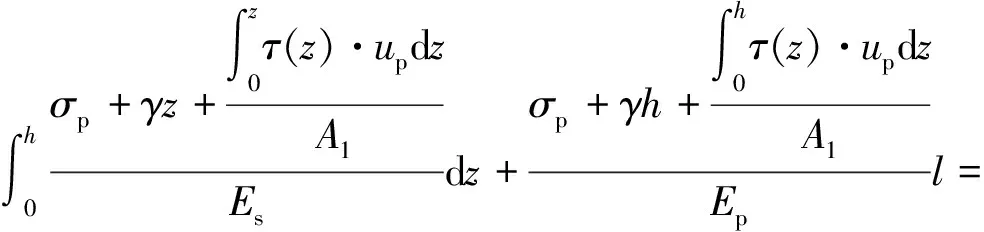
(12)
式中:σp——作用于铜盒上覆土表面的正应力;
σs——作用于下部试样上覆土表面正应力;
Es——土体压缩模量;
Ep——铜盒压缩模量;
τ(z)——随竖向深度变化的剪应力;
up——铜盒与土试样接触弧长;
γ——土试样重度;
h——上覆土体厚度;
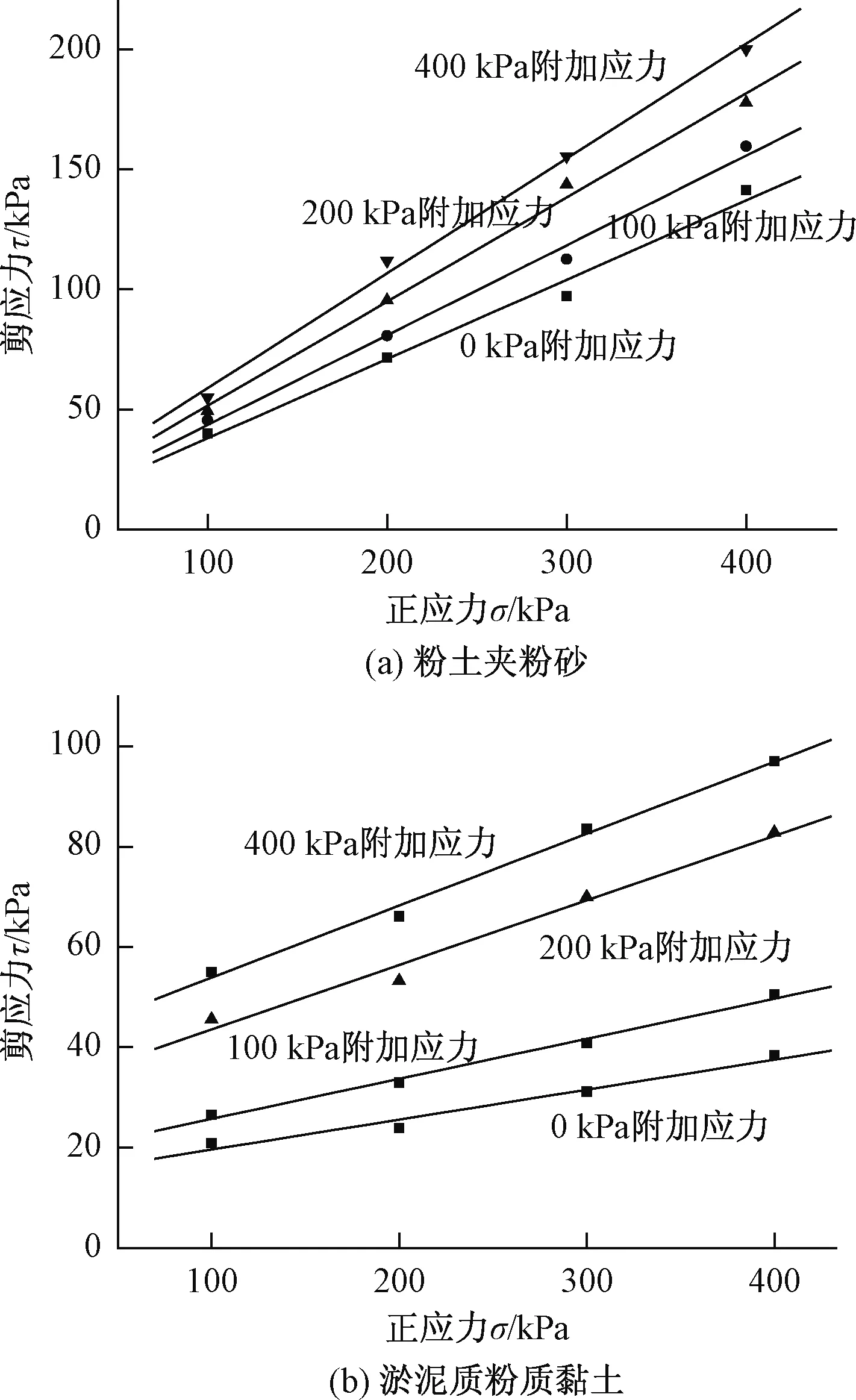
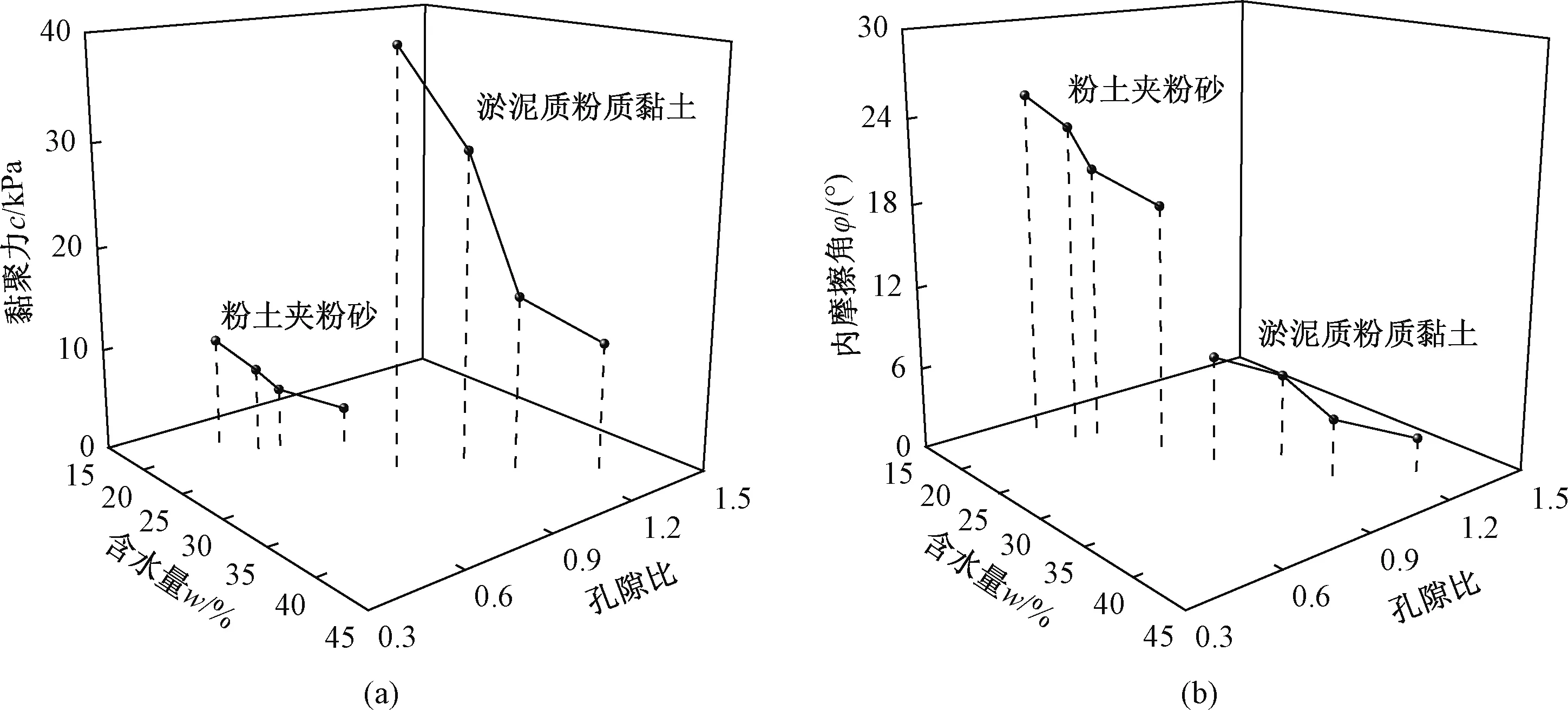
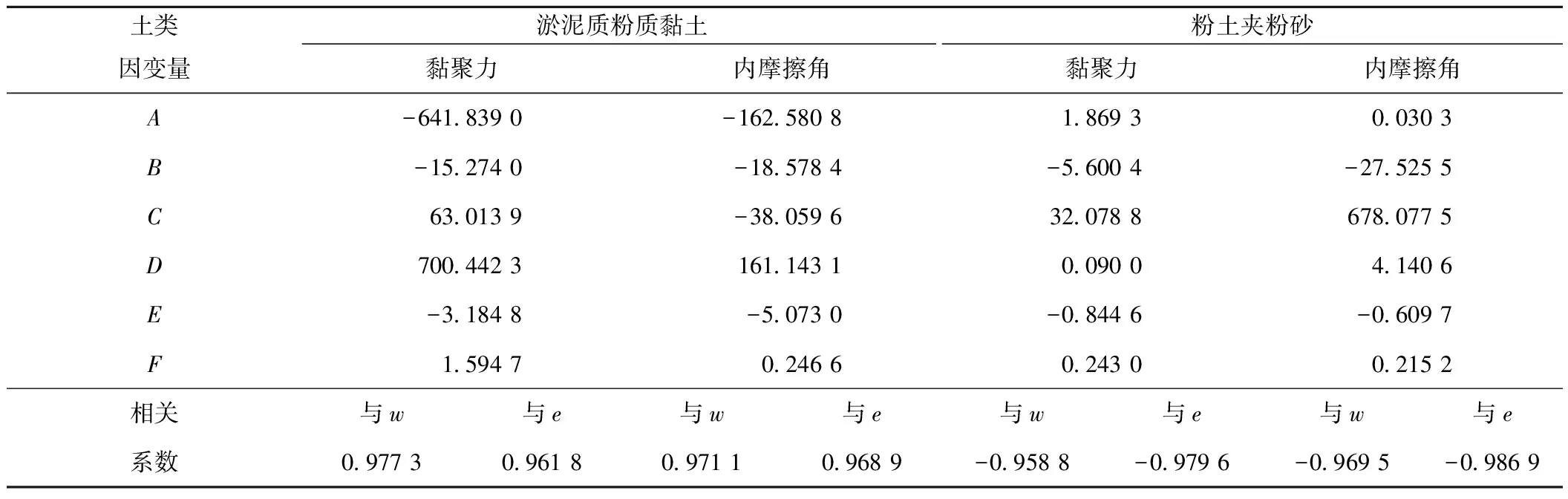
l——半个环刀高度;0 A1——剪切范围内铜盒所占面积; A2——剪切范围内土试样所占面积。 FN作用下铜盒与土两部分上覆土表应力分担如下: σpA1+σsA2=FN (13) 对图1左侧剪切面以上土体进行受力分析有: (14) 式中:σsh——上覆土h深度所受的竖向正应力。 据图6剪切面下部土体沉降变形与铜盒刺入上覆土层深度扣除铜盒压缩变形量值相等原则,得: (15) 式中:δ——铜盒刺入上覆土层深度。 借鉴刚体刺入垫层深度计算式[11]: (16) 取图5上覆土层深度z处微单元体,列竖向静力平衡方程: σszA2-(σsz+dσsz)A2+γA2dz-τ(z)·updz=0 (17) 式中:σsz——上覆土z深度处所受的竖向正应力。 将式(16)代入式(15)中与式(14)联立解得: (18) (19) 因剪应力相对于竖向应力对沉降变形的影响微弱,在此做线性简化假设: (20) 因受力面积满足:A1=A-A2 (21) 将式(17)~(21)代入式(12)中,联立式(13)可求得剪切过程中的正应力: (22) (23) (24) h=l(1-ε) (25) 式中:ε——竖向应变; 由式(22)、(23)、(24)可得: σs=σβ1-γhβ2 (26) Es与ε的变化与σ有关,而A2的变化与t有关,则β1,β2是受时间及附加应力双变量影响的参数,即β1=F1(σ,t),β2=F2(σ,t)。 通过快速固结试验,获取土体不同附加应力下的竖向变形量,与初始高度值相比,即可获得试样的竖向应变。称得固结后试样质量,调用前述基本物理性质试验指标参数,求取密度、孔隙比及饱和度的变化值。以常规固结试验测定再压缩模量。 各级附加应力下的土体试样竖向应变、含水量再压缩模量变化趋势如图7所示。图7表明,随附加应力的增长,两类土体的竖向应变均递增,但淤泥质粉质黏土的增长幅度要大于粉土夹粉砂。随附加应力增长,土体含水量均递减,且减少梯度大致相同。随附加应力的增长,土体压缩模量会逐渐提高。土骨架具有可变性,因受附加应力产生变形,土颗粒靠近变密,相互间胶联增强,骨架结构更趋稳定[12],表现出土次生结构的强化。 将粉土夹粉砂与淤泥质粉质黏土试样的各级附加应力施加后的密度、孔隙比及饱和度列于表2。 由表2可见,施加不同的附加应力,粉土夹粉砂与淤泥质粉质黏土的密度均会随其值增加而增大,而孔隙比则会随其增加而减小。在附加100 kPa压力下,密度与孔隙比变化迅速,但当所施压力成倍递增,其变化逐渐缓慢。因所选土样自身饱和度极高,附加应力的施加会促使土体更趋饱和乃至最终实现饱和。以上现象说明,施加的附加应力改变土体自身结构,使颗粒因外力作用脱离固有受力平衡状态而发生错动,颗粒与颗粒间咬合得更加紧密,土体内部空隙减小,颗粒相互接触面积增大。此外,侧限压缩过程会出现部分自由水随土骨架的重构筑排出土体表面现象,此时孔隙内封闭的气体也会部分排出,表现为饱和度的提高。 将各级附加应力作用快速固结后的环刀试样移至四联电动直剪仪中进行快剪试验,取峰值强度,以其所对应的强度指标值为试验结果,据图7所反映的关系曲线得出各附加应力所对应的ε及Es,由ε计算剪切时上覆土体厚度h;绘制面积变化如图8所示,求算峰值强度时间点对应的A2。 图8 剪切面积变化曲线Fig.8 Change in the dynamic shear area 代入式(22)中,求出作用在土体上的正应力σs,由式(7)求出τ,将所得正应力σs与切应力τ绘制成图9。将线性拟合后获取的抗剪强度参数列于表3。 由表3和图9可知,随附加应力的变化,粉土夹粉砂与淤泥质粉质黏土的抗剪强度参数均产生改变,但其影响有限,后续压力作用下土体抗剪强度参数变化渐小。随荷载增大,粉土夹粉砂的内摩擦角增长趋势明显,黏聚力变化较小,淤泥质粉质黏土则表现为黏聚力增长迅速而内摩擦角变化缓慢。 图9 各级附加应力下粉土夹粉砂和淤泥质粉质黏土的抗剪强度Fig.9 Shear strength of silt, silty sand and mucky silty under normal additional stress 附加压力/kPa0100200400粉土夹粉砂c/kPa4.906.108.1010.90φ/(°)18.2820.5223.4525.57淤泥质粉质黏土c/kPa13.7017.8030.7039.60φ/(°)3.424.567.338.16 随附加应力的施加,土体将产生竖向变形,宏观上表现为总体积缩小,伴随有部分水挤出土体表面。土中水分为自由水与结合水,附加应力下土体内部流态自由水被排出使得土颗粒间距缩小,水的黏滞性提高,因物理力与化学键作用而产生的黏着作用增强。 土体受附加应力压缩后,孔隙比减小,骨架调整使分布于剪切界面上的土颗粒数目增加,凸起或凹陷处增多,摩擦接触面积加大。摩擦机理表明剪切界面上实际接触面积仅占表观接触面积的小部分,随法向力的增大,实际接触面积会随之呈线性增长,摩擦阻力也随之加大[13],而粒间摩擦强度对宏观抗剪强度起决定性作用[14-15]。同时,非饱和细粒土中,毛细作用与土体内部的孔径有关,在微小孔隙贯通形成的毛细管周壁,水膜与空气分界面存在毛细张力,土颗粒骨架因此反受毛细压力作用。随孔隙比减小,毛细作用不断加大,颗粒间距缩小,粒间引力增长,宏观上表现为抗剪强度指标的改变。 如图10所示,随含水量与孔隙比的递减,淤泥质粉质黏土与粉土夹粉砂的黏聚力与内摩擦角均呈现递增趋势,淤泥质粉质黏土黏聚力增长较快,粉土夹粉砂则为内摩擦角增长较快。 两类土体呈现出抗剪强度指标变化的差异性与剪切界面的颗粒成份及粒径级配有关。黏土颗粒粒径小,具有胶结特性,颗粒经过长期的物理化学作用,会形成一定的胶结强度。颗粒粒径级配分析曲线所示,淤泥质粉质黏土中微小颗粒比粉土夹粉砂中的含量多,分布集中,土体总比表面积大,吸附更多的弱结合水。当含水量由可塑状态增至濒临流动状态时,颗粒间距拉大,受土中水润滑作用影响,咬合力比粉土夹粉砂表现得稍弱,呈现黏聚力较大程度的改变。粉土夹粉砂因较优良的粒径级配,附加应力的施加使颗粒紧凑,剪切界面上黏着接触节点生长更多,颗粒间物理力与化学键受影响加深,移动或滚动的难度增大,施加相同剪应力下内摩擦角明显变化。 通过分析图10可发现内摩擦角或黏聚力与含水量及孔隙比之间存在倒S型曲线模型[16]关系,由此构造函数关系式: (27) 式中:z——黏聚力或内摩擦角; x——含水量; y——孔隙比。 采用MATLAB对数据进行上述表达式拟合,效果较好(表4)。 图10 含水量、孔隙比与黏聚力、内摩擦角的关系Fig.10 Water content and void ratio vs cohesion and angle of internal friction 土类淤泥质粉质黏土粉土夹粉砂因变量黏聚力内摩擦角黏聚力内摩擦角A-641.839 0-162.580 81.869 30.030 3B-15.274 0-18.578 4-5.600 4-27.525 5C63.013 9-38.059 632.078 8678.077 5D700.442 3161.143 10.090 04.140 6E-3.184 8-5.073 0-0.844 6-0.609 7F1.594 70.246 60.243 00.215 2相关与w与e与w与e与w与e与w与e系数0.977 30.961 80.971 10.968 9-0.958 8-0.979 6-0.969 5-0.986 9 (1)考虑固结快剪试验中受剪土体与剪切盒各层面受力与沉降的关系,进行正应力求算,融入动态剪切面积表达式,推导正应力修正公式。 (2)附加应力的施加改变受剪土体抗剪强度指标值,指标值的变化因不同土体类型而表现出差异性,淤泥质粉质黏土以黏聚力变化为主,粉土夹粉砂以内摩擦角变化为主。 (3)土中含水量与孔隙比的减小,微观上体现为颗粒间距缩小,粒间接触面积增大,水的黏滞性提高,毛细作用与黏着作用增强,导致土体黏聚力与内摩擦角的改变。具体表现为抗剪强度指标值随含水量与孔隙比的递减而有所增长。 (4)土颗粒粒径越小黏聚力越易受水的影响;粒径级配越优良,内摩擦角变化越明显。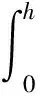
3 试验结果分析
3.1 附加应力对密度、孔隙比、饱和度的影响
3.2 快剪试验结果及分析
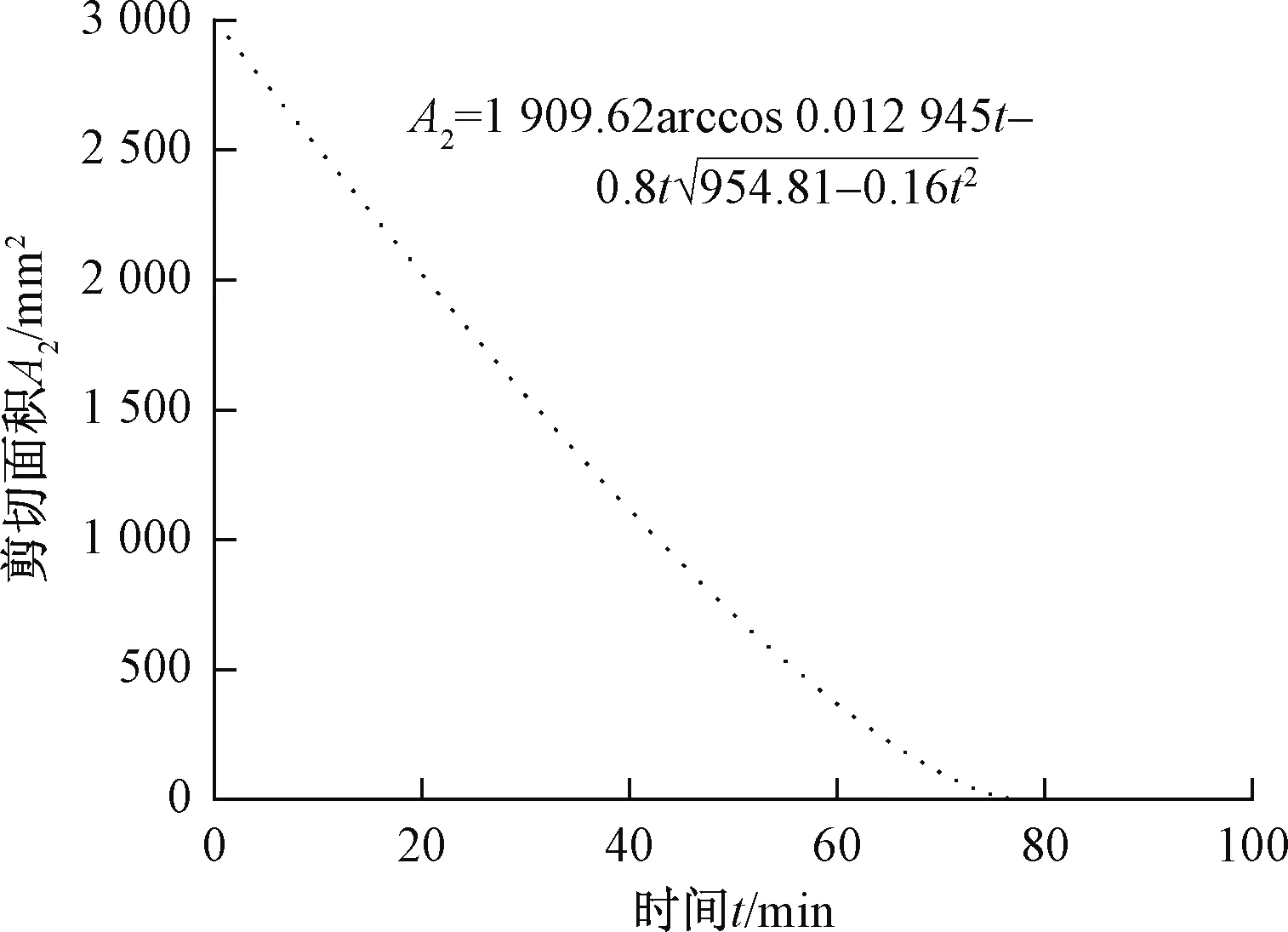

3.3 含水量、孔隙比耦合变化对黏聚力、内摩擦角的影响
4 结论

