爆燃压裂起裂模型常见问题分析与修正*

孙 林 黄 波 熊培祺

(中海油能源发展股份有限公司工程技术分公司 天津 300452)

爆燃压裂(也称为高能气体压裂、气动力造缝、脉冲压裂或推进剂压裂)技术是利用火药或火箭推进剂快速燃烧产生的高温高压气体使油气井增产增注的技术。该技术起源于19世纪60年代，用于向水井中开枪产生振动增加水量；直到20世纪60—70年代，前苏联和美国进行了大量现场实验和理论研究，使该技术发展起来。我国原西安石油学院与西安近代化学研究所于1986年3月在延长油矿七里村1038井进行了国内首次爆燃压裂现场实验并获得成功[1-6]；迄今为止，爆燃压裂技术在我国大庆、长庆、胜利、辽河、南海东部等油田应用已达上万井次，效果显著。

爆燃压裂技术的核心之一为峰值压力、裂缝参数等计算，为火药用量设计及作业安全性提供依据。我国从技术应用初期就开始从事这方面的研究工作，国内很多学者对常用起裂相关模型[7-15]进行了研究。但笔者在从事爆燃压裂模型研究过程中发现，目前国内文献中有关模型常出现一些问题，导致模型无法正常计算或者有关参数无法求解，而目前国内未对此问题进行相关修正，极易使相关研究产生错误，严重时可造成较大井下安全事故。针对此类问题，笔者推导分析了爆燃压裂起裂模型，并对相关模型错误进行修正。此外，针对原压挡液运动模型只能计算压挡液柱底部向上运动过程，而无法计算液柱中压力分布情况的问题，笔者根据牛顿第二定律和材料力学方程，按照压力波在液柱中的传递过程进行推导，新建立了一套应用范围更广的压挡液运动模型，从而整体提升了爆燃压裂预测精度和范围，为爆燃压裂参数预测和安全控制提供了理论参考。

1 常见问题分析

目前国内常见的爆燃压裂技术起裂模型主要包括火药燃烧模型、压挡液运动模型、热传导模型、液体模型(参数包括挤入垂直裂缝的液体流量、将液体挤入裂缝的压力)、气体模型(参数包括火药气密度、挤入垂直裂缝的气体流量、将气体挤入裂缝的压力)、裂缝模型(参数包括裂缝缝长、裂缝缝宽)等[7-14]，计算公式有十余个。将这些模型进行联合求解，即可得到具有有限精度的数值解，但这些模型存在单位不统一、物理意义模糊、模拟功能范围窄等问题，导致模型无法正常计算或者有关参数无法求解。

1.1 单位不统一

单位不统一的问题主要涉及压力、火药力、体积、密度、余容、杨氏模量等参量，本文主要分析爆燃压裂峰值压力简易模型和挤入液体模型。

1.1.1爆燃压裂峰值压力简易模型

爆燃压裂峰值压力简易模型[10-14]是早期实施爆燃压裂中常用的一种峰值压力预测方法，该方法具有计算便捷的特点，适用于计算精度不高的模拟。该模型的表达式如式(1)，整理后单位常见问题见表1。

(1)

表1 爆燃压裂峰值压力简易模型单位常见问题Table 1 Simple peak pressure model for deflagration fracturing about common unit problems

1.1.2挤入液体模型

挤入液体模型[7-9]是指在高压情况下，计算射孔孔眼内泄压时套管外压和挤入裂缝的液体流量的模型，该模型的表达式如式(2)、(3)，整理后单位常见问题见表2。

表2 挤入液体模型常见单位问题Table 2 Common unit problems for liquid model

(2)

(3)

1.2 物理意义模糊

物理意义模糊的问题主要涉及单位的系数合理性、相近量纲符号混用、未考虑地下状况等方面，本文主要分析压力与时间主模型、挤入液体模型、挤入气体模型和裂缝与时间关系模型等。

1) 压力与时间主模型。

压力与时间主模型[7-9]是计算不同时间下火药产生压力的关键公式，通过此公式可以预测不同火药用量下地层峰值压力大小，从而优选火药用量，确保管柱安全。该模型的表达式如式(4)。

(4)

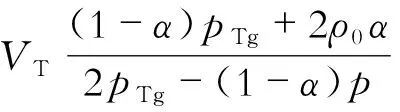
(5)

2) 挤入液体模型。

3) 挤入气体模型。

裂缝入口的爆燃压裂燃烧产物火药气的压力为

(6)

(7)

(8)

式(6)～(8)为常见的挤入气体模型[7-9]公式，其中：pTg为裂缝入口的爆燃压裂燃烧产物火药气的压力，Pa；a为裂缝指数，无因次；γ为燃烧产物的多变系数,无因次。

式(6)中的2p0同样存在物理意义不明确的问题；同时，国内部分模型易将p和ρ写错，把a的裂缝指数和火药余容α混用，导致公式无意义；式(7)、(8)均是表达气体流量的计算公式，但是气体具有压缩性，公式中仅考虑了地面情况，未考虑气体在地下受温度、压力影响下的实际流量，因此，考虑条件不全。

4) 裂缝与时间关系模型。

目前国内有2套公式计算裂缝的缝长和缝宽[7-9，15]，见式(9)、(10)。

(9)

(10)

式(9)、(10)中：L(t)为裂缝缝长，m；W(t)为裂缝缝宽，m；ρr为岩石密度，kg/m3；υ为岩石泊松比；E为杨氏模量，Pa；t为作用时间，s。

式(9)、(10)中 2p0项同样需要修正；另外式(9)中p-2p0项，由于起裂压力不断增加，当p=2p0(或修正后的pf)时，p-2p0值为0，将造成1个结果为无穷大的计算奇点。

1.3 模拟功能范围窄

目前模拟中通常采用刚体压挡液运动模型[7-9]，如式(11)、(12)。

(11)

(12)

式(11)、(12)中：x为气液界面位移距离，m；v为液柱质量中心的速度，m/s；p0为井筒液柱压力，Pa；ρ0为井筒液柱密度，kg/m3；C0为弱压缩波在井筒中的传播速度，m/s；β为井筒液柱和套管的摩擦系数；D为套管直径，m。

由于压挡液为可压缩流体，因此只能计算压挡液柱底部向上运动过程，无法计算液柱中压力分布情况。

2 模型修正

2.1 统一单位

单位不统一会导致计算数据的巨大差异，笔者在尽量保留原公式情况下，仅对计算单位进行统一。

2.1.1爆燃压裂峰值压力简易模型

经过推导，得到修正后的单位见表3。系列1中修正了V0的体积单位，同时为了跟其他单位的统一性，也修正了火药密度ρ单位；系列2中修正了压力单位错误问题。2个系列单位都可以进行使用。

表3 爆燃压裂峰值压力简易模型修正后的单位Table 3 Unit for deflagration fracturing peak pressure after correcting

2.1.2挤入液体模型

同理，采用不同单位进行推导，在同时满足式(2)、(3)单位的正确性且不修改原公式的情况下，各物理量单位见表4。

表4 挤入液体模型修正后的单位Table 4 Corrected unit for liquid model

2.2 物理意义修正

2.2.1压力与时间主模型

对式(4)修正为

(13)

2.2.2挤入液体模型

为了保证公式物理意义更符合实际情况，因此将2p0修正为pf，式(3)修正为

(14)

2.2.3挤入气体模型

综合物理意义和考虑条件不全问题，将气体体积流量都修正为地下状态，在公式中增加Bg(气体压缩因子，无因次)项，式(6)～(8)修正为

(15)

(16)

(17)

2.2.4裂缝与时间关系模型

式(10)修正为

(18)

2.3 扩大模拟功能范围

有文献[16-17]研究解决模型模拟功能范围窄的问题。本文根据牛顿第二定律和材料力学方程，按照压力波在液柱中的传递过程进行推导。

压挡液柱的运动，实际上是压力波在液柱中传导的一个过程，这个传播过程具有波动方程的形式。以微元液体进行力学分析，如图1所示，可以得到

(19)

式(19)中：[(pL+ΔpL)-pL]A为微元体积力的差值，Pa，其中pL为微元压力值，ΔpL为微元压力变化量，A为微元面积；f为运动阻力，主要包含流动摩擦力和重力，Pa；m为微元质量，kg；u(x,t)为压挡液中微元在x位置处、t时刻的位移，m。

图1 微元液体示意图Fig.1 Schematic diagram of micro liquid

根据材料力学方程，可压缩材料(即材料的杨氏模量E的值较小)的体积力和压缩量的关系为

(20)

将运动阻力展开

(21)

同时，微元的运动速度表达式为

v=[∂u(x,t)]/∂t

(22)

则最终的可压缩液体的运动方程为

(23)

(24)

边界条件为

u(x,0)=0

(25)

(26)

(27)

式(20)～(27)中：E0为水的体积模量，Pa；ρ(x,t)为压挡液中微元在x位置处、t时刻的密度，kg/m3；ρ0为压挡液原始密度，kg/m3；λ为摩阻系数；r为井筒半径，m；pL(t)为t时刻微元压力，Pa。

通过式(20)、(23)、(24)联解，即可求得压挡液中微元在x位置处、t时刻的压差值ΔpL，从而得到压力分布和传播情况。

3 应用分析

自2014年5月利用修正后的压挡液运动新模型已在中国海上油田应用8井次，其峰值压力经过检测，修正模型计算精度达97%。如南海东部油田X井爆燃压裂施工时井下高速压力计测试值为132.23 MPa，采用修正模型的软件预测值为127.77 MPa，如图2所示，而采用峰值压力简易模型的预测值仅为110.44 MPa。由此可见，修正后的新模型计算结果与现场测试数据吻合较好,可为爆燃压裂参数预测和安全控制提供参考。

图2 本文修正模型计算的南海东部油田X井爆燃压裂峰值压力Fig.2 Peak pressure of Well X in eastern South China Sea calculated by corrected model in this paper

4 结论

1) 通过公式单位推导与物理意义分析，对爆燃压裂峰值压力简易模型、挤入液体模型中的单位不统一问题和压力与时间主模型、挤入液体模型、挤入气体模型和裂缝与时间关系模型物理意义模糊问题进行了修正；同时根据牛顿第二定律和材料力学方程，按照压力波在液柱中的传递过程进行推导，建立了一套应用范围更广的压挡液运动新模型。

2) 压挡液运动新模型在中国海上油田成功应用8井次，峰值压力计算精度达97%，具有较好的推广应用价值。