PT对称波导中周期势的调制对相变的影响

胡蕊,郭利平

(山西大学 理论物理研究所,山西 太原 030006)

0 引言

PT对称的研究最早是在光波导实现的[8]。波导折射率n(x)=n1(x)+in2(x),其中描述线性材料的基础折射率的实部n1(x)满足偶宇称,n2(x)满足奇宇称,用于表征材料的增益和耗散的虚部,因此n(x)=n*(-x).则由折射率决定的势函数满足[9-13]

U(x)=U*(-x) .

(1)

当光在波导中传播时,麦克斯韦方程在傍轴近似下的光传播方程类似于含时薛定谔方程[14-18],另外改变波导的弯曲程度可提供必要的驱动外场[19-20]。当周期势的实部和虚部的周期相同,且实部振幅大于虚部振幅时,系统的哈密顿量处于PT对称区域;当实部振幅小于虚部振幅时,PT对称发生破缺;两个振幅相等时是奇异点。当周期势的实部和虚部周期不同时,其对PT对称区间以及能谱的影响是本文研究的重点。

1 理论模型

我们研究波长为λ的单色光在(X,Z)平面光波导阵列中的传输情况。其中光波导阵列是沿X方向且等间距排列,其间距为a。如果波导沿Z方向是弯曲的,且弯曲程度都一致用X0(Z)=Asin(ωZ)来描述,其中A是波导管弯曲程度的振幅,ω是其频率。

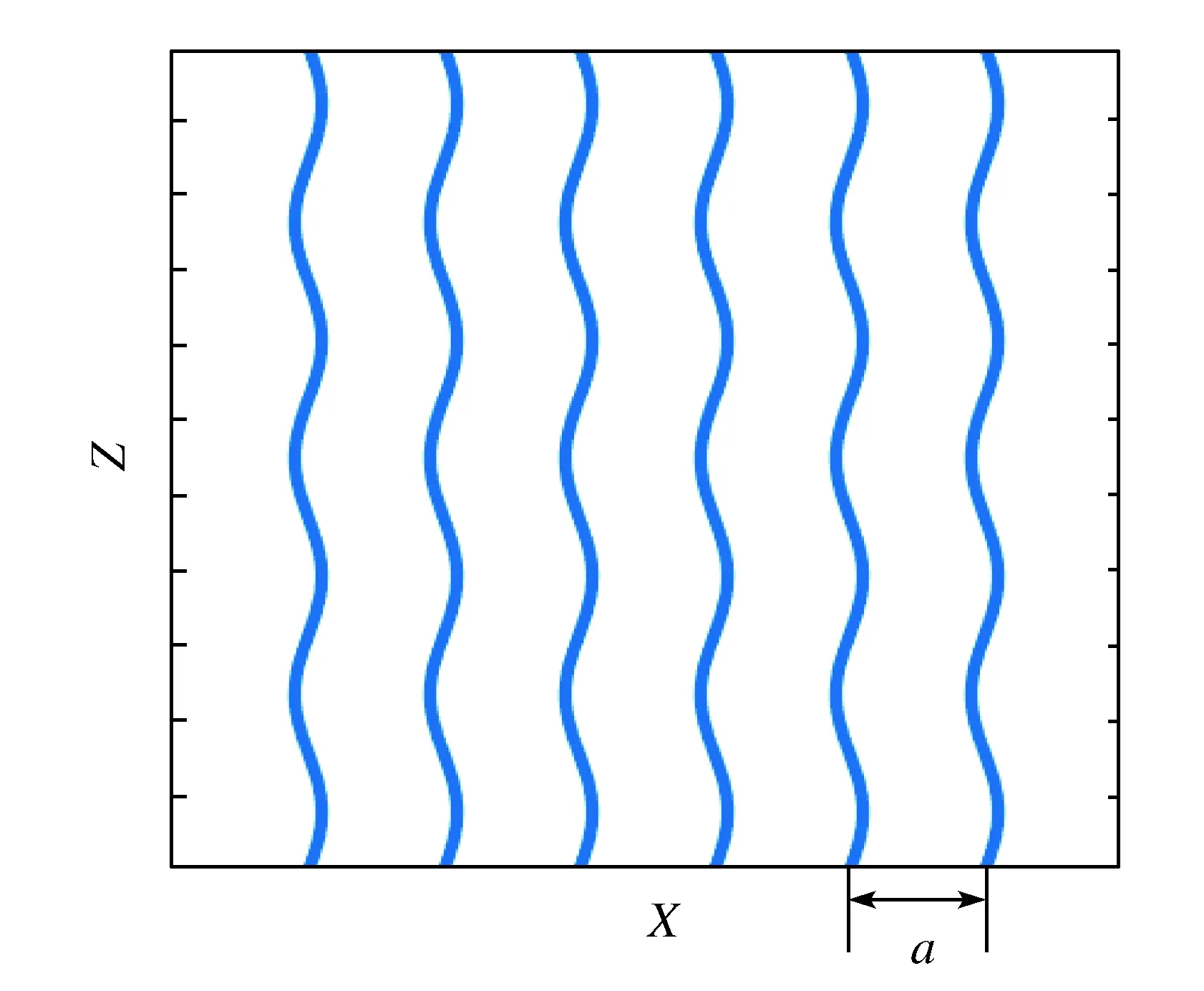
Fig.1 Waveguide array schematic diagram图1 波导阵列示意图

描述电场振幅ψ的有效传播方程为[19]

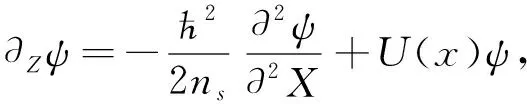
(2)

其中ћ=λ/2π,ns是基质折射率,x=X-X0(Z),U(x)=ns-n(x),n(x)是波导阵列的有效折射率且周期为a,即n(x)=n(x+a).利用规范变换

(3)

(点表示对Z求导),方程(2)变为[19]

iћ∂ZΨ=H0Ψ-F(Z)xΨ,

(4)

其中

(5)

周期驱动力

F(Z)=nsAω2sin(ωZ),

(6)

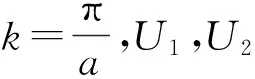
本文着重研究周期势的实部和虚部周期不同时对PT对称及能谱的影响。考虑势函数为

U(x)=U1cos(2kx)+iU2sin(4kx),

(7)

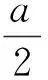
(8)

(9)

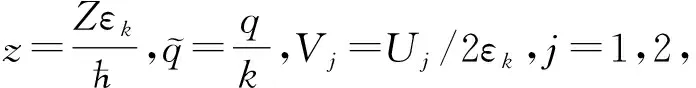
i∂z|aq(z)〉=H0|aq(z)〉,

(10)

其哈密顿量可以写成下面的形式

(11)

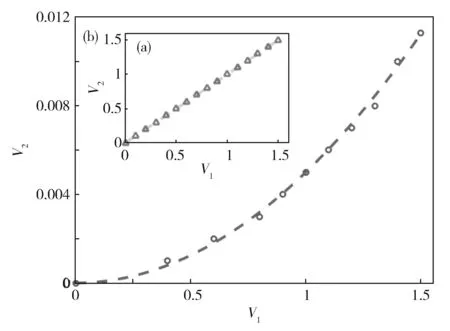
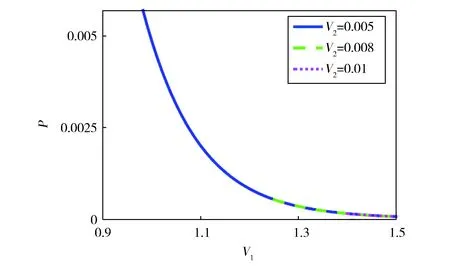
我们可以发现H0†≠H0,虽然每个矩阵元是实数,但(11)式是非厄米的哈密顿量。文献[18]研究的哈密顿量非对角元只出现在近邻对角线上,而(11)式中则出现了次近邻项。通过101个波导数值计算发现:文献[18]中研究的结果V1=V2是奇异点发生的条件(如图2(a)三角符号所示,虚线是数值拟合函数)。在图2(a)中当V2

结果表明由于势函数实部和虚部的周期不同，PT对称区域缩小了。通过拟合发现V1和V2满足以下关系:

(12)

另一方面,我们考虑周期势函数形式为

U(x)=U1cos(2kx)+iU2sin(6kx),

(13)

(14)

Fig.2 (a) Relation diagram of V1 and V2 at Exceptional points in [20].(b) Relation diagram of V1 and V2 at Exceptional points from Eq (11).图2 (a)文献[20]中奇异点V1和V2的关系图;(b)方程(11)奇异点V1和V2的关系图

Fig.3 Energy bands of the system as a function of Bloch-momentum and (b) describe thereal and imaginary part of the three lowest bands when respectively. And (c) and (d) show the cases when (a)、(b)当时描述了三个最低能带的实部和虚部;(c)、(d)分别表示的情况。图3 系统的能带是布洛赫动量的函数

将(14)式写成演化方程(10)的形式,其哈密顿量可表示为

(15)

在本文中近轴弯曲导致的交替驱动力(6)作用下准动量随时间的演化为

q(Z)=q0-nsAωcos(ωZ),

(16)

我们主要集中观察在PT对称区间对应的最低两能带能级免交叉点处的动力学问题。根据Landau-Zener隧穿概率公式[21]

(17)

其中,Δ为免交叉点处的能隙,v为能量变化的速率。以势函数(7)下的能谱为例进行研究,根据数值结果(12),在PT对称区间中每取定一组V1,V2的值就会有唯一的Δ和v与之对应,从而利用(17)式计算出Landau-Zener隧穿的隧穿概率。如图4所示可观察到由于V2远小于V1,隧穿概率随着V1增大而减小,不随V2的变化而变化。

Fig.4 Landau-Zener tunneling probability as a function of V1 with different V2.图4 V2取不同值时，Landau-Zener隧穿概率随V1的变化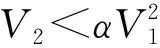

2 结论