多类型公共自行车调运问题

徐国勋， 李妍峰， 李 军， 徐冠宇

(1.西南交通大学 经济管理学院，四川 成都 610031；2.成都飞机工业有限公司，四川 成都 610000)

0 引言

随着城市化进程的不断加快，城市交通拥堵问题日益严峻，给居民出行带来诸多不便。自杭州2008在国内建立第一个公共自行车系统以来，我国城市公共自行车系统的建设取得了长足的发展。截止2016年初，我国共有118个城市拥有公共自行车系统[1]。公共自行车可以有效衔接长距离公共交通，与短距离公共交通形成优势互补，可以替代部分私家车出行，因而已经成为城市公共交通系统的重要组成部分。同时，公共自行车还是一种零碳排放的出行工具，符合未来智慧城市的发展方向。

随着公共自行车系统的大量建设和推广，越来越多的问题产生并亟需解决。倪康康等[2]对国内公共自行车系统的发展状况进行了分析，指出目前公共自行车系统运营过程中亟待解决的问题主要有：(1)道路骑行的安全问题；(2)道路的交通管理问题；(3)公共自行车借车难、还车难、易损坏；(4)公共自行车系统设备安装运营以及亏损问题。借车难、还车难是阻碍公共自行车系统发展的主要问题，即在需要租车的时候发现站点无车，在需要还车的时候发现站点无空位。为解决此类难题，需要进行合理有效的车辆调运，即调运卡车在公共自行车租赁站点所组成的网络中，将某些站点的自行车调运到其它站点去。这类问题被称为自行车调运问题或者自行车再平衡问题。这类问题的研究又分为动态和静态两种。当自行车系统使用率非常高时，根据每个站点的实时需求进行实施调运。当自行车系统使用率较低时，选择在某个时段内(如夜间)对各站点进行调运。由于自行车系统一般是在晚上进行调运，因此现有研究以静态模型为主，而对动态问题的研究非常少，只有文献[3～7]进行了研究。无论是动态问题还是静态问题，已有研究主要以运营成本最小和为满足的需求最小为目标，或是采用线性加权的方法同时考虑着两个目标。

通过对已有文献的梳理，发现目前对静态公共自行车的研究，除了Li等[17]之外都只针对单类型自行车，多类型自行车的研究处在起步阶段。在实际中，很多城市(如中国的杭州、台北，荷兰的鹿特丹、海牙、乌得勒支，英国的伦敦，日本的爱知县等)已经开始将多类型公自行车(如单人座，双人座，带小孩座椅等)引入公共自行车系统，在景区中(如杭州西湖，武汉东湖等)更加普遍也更加受欢迎。针对多类型公共自行车的特点，本文做了以下研究：(1)提出了多类型公共自行车的再平衡问题。针对网络中各类型自行车失衡的情况(如地铁站附近很难租到单人座自行车，景点附近很难租到双人座自行车等等)，设计了一个惩罚系数。该系数除了能衡量站内已有自行车数目和目标需求的偏差，还可以实现各租赁站点公共自行车的调运组合优化。(2)考虑了调配时间的限制。在现实生活中，对公共自行车的调配一般集中在某个时段(例如夜间)，因此本文将调配时间限制引入到多类型公共自行车问题。(3)将配送车辆数目扩展至多辆车。Li等[17]对多类型自行车的研究是假定一辆调运车负责所有租赁站点的调运，而在现实中是由第三方物流公司派出多辆调运车辆服务租赁站点。为了使问题更加贴近实际情况，本文研究了多辆调运车辆的情况。

1 问题描述及模型建立

1.1 问题描述

本问题定义在完备图G=(V,A)上。V表示点的集合{0,1…,n}，包括车场和租赁站点，其中0点表示车场，其余为租赁站点。由于自行车调运有第三方物流公司运作，因此车场内自行车保有数量为0。A表示弧的集合，A={(i,j);i,j∈V,i≠j}，每条弧对应着一个运输成本。

此外，本问题考虑了不同类型车辆之间需求的替代性。即某类自行车缺货时，有可能由其他类自行车替代使用。若某站点没有单人自行车，租赁者可使用双人自行车作为替代。反之，若使用者想租赁一辆双人自行车，而站点没有此类车时，可转向使用2辆单人自行车作为替代。而某些情形则不允许替代，如带小孩的租赁者打算租赁一辆带小孩座椅的自行车，但该站点没有此类车，这时租赁者没有办法使用其他类自行车作为替代。替代策略可以有效缓解需求，但同时也会产生一个替代惩罚成本，这是由于它的替代，会导致其他站点可供此类自行车使用的数量减少。

本问题需要合理地安排车辆的调运路线，同时确定在每个站点每类自行车的装载或卸载数量，从而使得总成本(包括公共自行车运营公司支付给物流公司的运输成本、非均衡惩罚成本和替代惩罚成本)最小化。

2.2 符号说明

在建模过程中需要用到以下符号：

(1)集合

K:调运车辆集合；M:行车种类集合；N:租赁站点集合。

(2)参数

(3)决策变量

2.3 数学模型

(1)

s.t.

辅助约束：

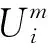
(2)

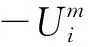
(3)

装卸载约束:

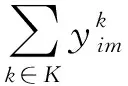
(4)

(5)

(6)

(7)

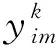
(8)

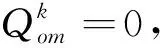
(9)

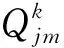
(10)

(11)

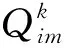
(12)

(13)

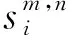
(14)

路径约束：

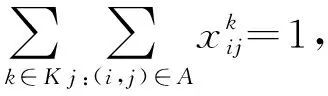
(15)

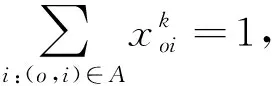
(16)

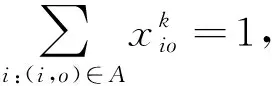
(17)

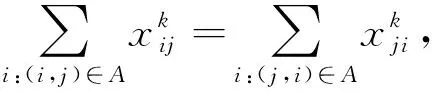
(18)

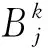
(19)

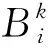
(20)

其它约束：

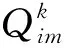
(21)

(22)

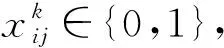
(23)

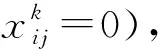
3 求解算法

由于本问题是混合整数规划问题，因此是NP问题。当问题规模较小的时候可以用Gurobi，CPLEX等商业优化软件求解，但当问题规模变大后，这些商业优化软件在规定的时间内甚至无法求得可行解。因此，本文设计了一种混合禁忌搜索算法来求解本问题。在所有的启发式算法中，禁忌搜索算法可以在较短时间内成功求解TSP问题(如文献[24])，VRP问题(如文献[25])，dial-a-ride问题(如文献[26～28])，Pickup and delivery问题(如文献[29,30])等一系列路线优化问题。考虑到公共自行车问题也是一类路线优化问题，故本文亦采用禁忌搜索算法作为主干算法，用来确定调运车辆的路线。当路线被确定后，本文将大规模数学规划优化器Gurobi 7.0嵌入到禁忌搜索算法中，用以确定多类型公共自行车的调运策略。算法具体流程如下所示：

Step1生成当前可行解p；

Step2用p更新Pbest；

Step3将精英集合S设为空集；

Step4如果满足终止条件转Step15，否则继续执行Step5～12，否则转Step13；

Step5在p的领域中找到最好的解p′；

Step6如果p′优于pbest，用p′更新pbest；

Step7将pbest放入精英集合S，然后更新精英集合S；

Step8用p′更新p；

Step9如果经过IT次迭代仍无法改进pbest，则执行Step10～12；

Step10从精英集合S中随机选出一个解pr，然后将pr从S删除；

Step11用pr更新p；

Step12重置禁忌表；

Step13返回pbest。

Step 1～3是算法的初始化步骤。在每次迭代过程中采用了最先改进下降策略来寻找最好的解(Step 5)。根据本文所设计的藐视准则，无法改进pbest的移动不能放入禁忌表中。如果pbest得到了改进，则将pbest放入精英集合S中(Step6～8)。如果经过次迭代仍无法改进pbest，则从精英集合中随机选出一个解pr，然后更新当前解p，并将禁忌表清空(Step 9～12)。

3.1 解的表示

假定n个租赁站点由k辆调运车辆来服务，则解p的长度为(k+n)。其中k个0表示从车场出发的调运车辆，其余n个自然数表示各个需要被服务的租赁站点。图1给出了k=3，n=7的例子，表示了3条路线：0→1→2→0,0→5→7→4→0和0→6→3→0。

0120574063

图1 解的表示

3.2 初始解的生成

本文设计了一种随机选择机制的最近邻算法来生成初始可行解。传统的最近邻算法在每次迭代中选择的是最近的且未被访问的站点，通过这种简单的贪心机制来构造可行解。本文所设计的算法用随机选择机制替代了简单的贪心机制。算法流程如下：

Step1将客户点集合S初始化为φ；

Step2将路线的初始点设置为0；

Step3在所有未被服务过的站点中选择总成本fcost最小的三个站点，随机选取一个站点j加入到路线末端的站点i之后，然后将j放入S中；

Step4如果未被服务过的站点只剩s,t最后两个，则二者被优先访问的概率为Ps和Pt的关系为Ps+Pt=1，Ps和Pr随机分布于区间(0,1)；

Step5如果S包含所有客户点，继续执行以下步骤，否则转Step 3；

Step6将剩余k-1个0点随机插入到路线当中，构造成3.1节表示的解；

Step7如果生成的解不满足服务时间守恒条件，则转Step 1，否则算法结束。

在Step 3中，fcost的计算公式如式(22)所示。

(22)

3.3 解的评估

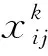
3.4 邻域算子

邻域算子是用来从当前解中生成新的解。本文设计了6中邻域算子，分别是：子序列随机交换，单点随机插入，子序列随机插入，子序列逆序，子序列逆序后随机插入和子序列逆序后随机交换。在每次迭代过程中，每个邻域算子采用均最先改进下降策略：一旦某个算子改进了当前解，则局部搜索从改进后新的当前解重新开始，直到所有邻域算子都无法改进当前解为止。

图2 邻域算子

①子序列随机交换：在解中随机选择两条独立的子序列，交换这两条序列的位置。如图2-a所示。

②单点随机插入：在解中随机删除一个点，然后将这个被删除点重新随机插入到解中。如图2-b所示。

③子序列随机插入：在解中随机删除一条子序列，然后将这个被删除的子序列重新随机插入到解中。如图2-c所示。

④子序列逆序：在解中随机选择一条子序列，然后将该序列逆序。如图2-d所示。

⑤子路线逆序后随机插入：在解中随机选择一条子序列并删除，然后将该序列逆序后随机插入到解中。如图2-e所示。

⑥子路线逆序后随机交换：在解中随机选择两条独立的子序列并且逆序，然后交换这两条序列的位置。如图2-f所示。

3.5 禁忌表和藐视准则

3.6 多样化策略

本文设计了一种基于精英集合的多样化策略。Nguyen等[31]设计了一种精英集合，此集合是由高品质解组成的具有多样性特征的解池，其中这些高品质的解在禁忌搜索算法迭代过程中发现的。当算法开始停滞时，精英集合可以使得算法更好地跳出局部最优，使得搜索方向朝着全局最优前进。

精英集合有最大规模上限，并且在算法开始的时候是空集。精英集合的多样性是通过不断地加入新的高质量的解，并删除现有的存在于集合中的某些解来实现的。与Nguyen等[31]的做法不同，本文对解的删除是基于解之间的相似度来决定。相似度Δ(pi,pj)表示解pi和pj之间相同弧的总数，其中Δ(pi,pj)≤n-1，n表示站点的数目，若有Δ(pi,pj)=n-1，则解pi和pj完全相同。举例如下，假定解p1=(0,1,2,3,4,0,5,6,7,8),p2=(0,1,2,5,4,0,6,8,3,7)，则p1和p2之间相同弧为(0,1)和(1,2)，因此Δ(p1,p2)=2。算法每次迭代都会将产生的最好的解pbest放入精英集合，但对解做删除操作时需考虑两种情况：1)当精英集合未达到规模上限时，将满足条件Δ(p,pbest)≥n-2的解全部删除，目的是提高精英集合的质量和多样性。2)当精英集合达到规模上限时，删除与pbest相似度最高的解即可。

4 数值实验

本节通过数值实验对问题特性进行了描述，并对算法性能进行了分析。混合禁忌搜索算法采用C#编写，所有实验均在i7-2600CPU主频3.40GHz内存16GB的PC上进行。

4.1 非均衡惩罚系数对调运决策的影响

表1 算例参数设置

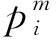
场景1基本场景。

场景2租赁站点2双人座自行车需求量很大，保有量无法满足需求，需增加调入量。

场景3租赁站点3双人座自行车的需求量很小，同时保有量过多，需增加调出量。

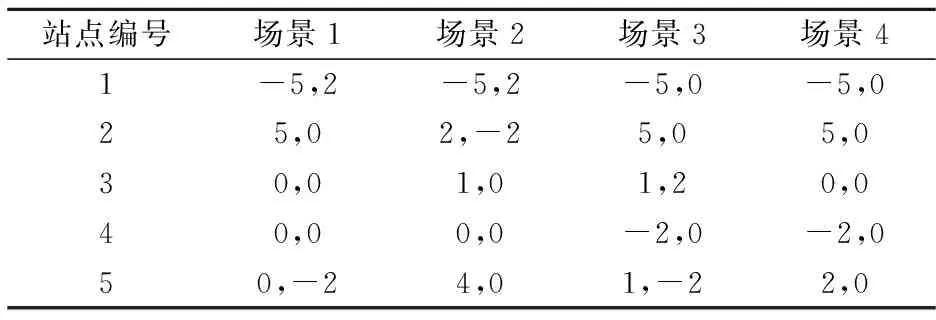
表2 四种场景下各类型自行车的调运数量

注：表中负值表示从配送车上卸载，即站点自行车增加。同理，正值表示往配送车上装载，即站点自行车减少。

表3 四种场景下目标函数值和调运车辆路线

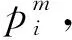
表3给出了4中场景下调运车辆的运行路线以及目标函数值。与场景1相比，场景2，3和4的目标函数值和运行路线都发生了变化。这是由于，不同的惩罚系数会产生了如表2所示不同的自行车调运组合，进而产生了不同了惩罚成本。同时，不同的调运组合会影响调运车辆的访问顺序，故产生了不同的运行路线。

4.2 替代策略对调运决策的影响

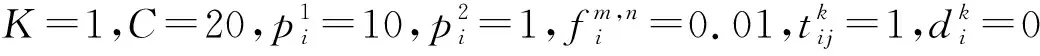
表4 不同替代策略下的结果

表4结果表明替代策略能够获得更低成本，因为第一类自行车具有相对较高的非均衡单位惩罚成本，采用替代策略能够降低第一类自行车非均衡的程度，并使得总的成本降低。该分析表明调运方在操作过程中可采取更加灵活的替代策略，以满足不同类型自行车的需求。

4.3 混合禁忌搜索性能分析

Nguyen等[31]发现精英集合规模增加到一定程度后，对解得改进作用开始不显著。他们的实验结果表明精英集合规模为5时，可以在解的质量和求解时间之间达到均衡。本文采用Nguyen等[30]的做法，将精英集合规模设置为5。此外出于求解时间的考虑，本文将设置为10，算法终止时间设置为100代。

表5 算法性能比较

表5详细给出全部数据的求解结果，Gurobi求解模型(终止时间为2小时)得到的上界(UB)、下界(LB)和反应Gurobi求解质量的gap。表5还给出了混合禁忌搜索求解结果，包括运行20次得到的求得的目标函数平均值(Avg.obj.)，平均运行时间(Avg.cpu)和标准差(Std)，以及反应与Gurobi求解下界(LB)差距的相关gap，其中gap=(Avg.obj-LB)/LB。

当|N|=10，Gurobi运行约100秒后求得了最优解。当问题规模逐渐增大(|N|=20,30,60,90)，gap逐渐变大，这种情形下Gurobi在规定时间内只得到了可行解。当问题规模进一步变大(|N|=120，Gurobi在规定的时间内无法求得可行解。这表明精确求解方法求解本问题上具有很大局限性。而文本所设计的混合禁忌搜索算法稳定性较好(标准差均值约25)，同时能在短时间内(平均运行时间不到4分钟)可求得所有规模数据的可行解，与精确算法形成了明显的对比。

为了比较混合禁忌搜索算法的求解质量，计算了相对于Gurobi求解下界的gap。由表5可得，当|N|=10，gap=0.2%，而平均运行时间约8秒。这意味着当问题规模较小的时候，混合禁忌搜索算法可在非常短的时间内求得十分接近最优值的可行解。当|N|=20,30，混合禁忌搜索求解gap虽然高于Gurobi求解gap，但差距在逐渐变小。当|N|=60,90，混合禁忌搜索求解gap比Gurobi求解gap要小，这意味着前者在600秒内求解效果比Gurobi求解两小时还要好。当|N|=120，混合禁忌搜索在短时间内仍然可以求得可行解。

5 结束语

本文研究了静态环境下多类型公共自行车问题，以运营成本最小目标建立了相应的混合整数规划模型。为求解问题，设计了混合禁忌搜索算法。其中禁忌搜索用来处理调运车辆路线的搜索空间，而租赁站点的各类型公共自行车的调配组合由嵌入的精确算法来确定。在数值分析部分，通过不同规模的算例比较，测试了混合禁忌搜索的性能。结果混合禁忌搜索能在较短时间内求解更大规模的问题，并且求解质量较好。测试算例还展示了非均衡惩罚系数对调配策略的影响，结果表明非均衡惩罚系数的变化可以决定了租赁站点各类自行车数量的增减和调配车辆的运行路线，本问题引入的惩罚系数成功地实现了不同租赁站点的公共自行车调运组合优化的目标。不同类型的自行车需求的替代使得调运决策更加灵活。下一步研究可考虑对损坏自行车的回收，动态环境下的调运以及和共享单车的比较等等。