基于学生能力发展的教学思考与尝试

王新星

(江苏省通州高级中学 226300)

一、问题提出

师：很多同学在参数范围问题的求解上表现得思路不清、计算模糊、解题不规范，今天我们就这一问题作详细探讨.

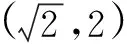
请各学生小组讨论并由各组代表展示交流成果.

师：这是惯常所用的数形结合法，生1的思路与表达都是值得肯定的，不过运算量大也导致无法得到最终结果，大家想一想参数范围问题可有更好解法呢？

生2：一般都用分离参数法，但本题的参数因为含有a2而无法直接分离出，此法对本题也不适合.

师：可有办法将参数分离呢？

生3：进行整体分离，例如，m2+m≥2sinx对x∈R恒成立，m的取值范围可以求得.

师：很好，大家都来试试看.

二、方法尝试

师：分析深入，条理清晰，非常好，大家可否对上述解题过程谈谈体会呢？

生5：分离参数的意识在解决此类问题时是必须的，整体分离解决本题时也表现出了解题的灵活性.

师(追问)：那么参数不好分离的情况是否还有呢？

生6：参数的系数符号不确定时就不能直接分离参数，例如：mx≤2x2+1，x∈R恒成立，求m的范围.不等号的方向在分离参数时并不确定，应怎么办呢？

三、思维发展

师：此时可以通过分类来解决问题，大家再看以下一题.

问题2 设函数f(x)=ax3-3x+1，若x∈[-1,1]时，f(x)≥0恒成立，求实数a的取值范围.

这是一道涉及众多知识与思想方法的综合题，教师在此题的教学中应进行充分的预设并启发学生的思维.

学生展示：

生7：因为x∈[-1,1]，因此分三种情况进行讨论：

(1)若x=0，f(x)=1≥0恒成立；

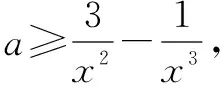
综合(1)(2)(3)，可得a=4.

师：大家解决上述两题之后可有什么收获和感受呢？

生8：很多问题的解决中虽有方法，但因为特定环境的改变会存在新的问题，改变思维方式并想办法进行克服才能更好地解决问题.

师：分离参数中一旦产生新的问题就需要解题的决心与能力作为支撑了.

问题3 设f(x)是定义在x∈[-1,1]上的奇函数，函数g(x)和f(x)的图象关于y轴对称，且当x∈[0,1]时，g(x)=lnx-ax2. (1)求函数f(x)的解析式；(2)若对于区间(0,1]上任意x都有|f(x)|≥1成立，求实数a的取值范围.

师：处理|f(x)|≥1是解决本题的关键，去绝对值符号采用平方法还是绝对值定义是需要考虑的.

生9：平方比较复杂.

师：那大家赶紧来解题吧.

四、能力提升

师：从上题可知，分离参数在包含绝对值不等式恒成立的问题中照样可以进行，借鉴这一思维也可以对含有二元变量方程的有解问题进行分析和处理，就是分离其中一个变量并用另一个变量表示，再结合其它条件进行解的判断与求值.

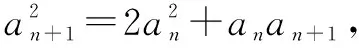
师：n到此处是否已经分离到位了呢？如果没有，又该怎样继续呢？

师：很好，分离到位了，解题就不难了，由此可见，分离参数是数学方法、思想和能力的综合.

总之，教师在具体教学中应不断为学生创设探究的机会并将其贯穿于整个高中数学教学中，唯有如此学生的能力与素养才能获得最大化的发展.