一种异方差模型的两阶段估计
张晓琴,牛建永,李顺勇
(1.山西财经大学 统计学院,山西 太原 030006;2.山西大学 数学科学学院,山西 太原 030006)
一、引 言
当经典线性回归模型的其它假设满足而同方差假设不满足时,称这样的模型为异方差模型。在截面数据中异方差性经常出现,当线性回归模型出现了异方差时,会对模型的估计和检验造成不良后果。研究线性回归模型主要是用于对模型进行估计和预测,而对模型进行估计和预测的前提是要确保模型具有一定的正确性和精确性。若对异方差线性回归模型进行最小二乘(OLS)估计会导致模型的估计与预测的精度降低,这就需要对其异方差问题进行有效的处理。
传统的处理异方差问题的方法主要有广义最小二乘法(GLS)、可行广义最小二乘法(FGLS)、Box-Cox变换法[1]等。近年来,国内外一些学者提出了处理异方差问题的不同方法如下:Su L等提出了使用局部多项式估计异方差多元线性回归模型[2];何其祥等提出了用局部多项式回归估计一元异方差线性回归模型[3],这两种方法均是使用局部多项式估计法估计模型的参数,虽然局部多项式估计具有一定的精确性,但在维数较高时带宽矩阵的选择是难点,因而此方法在多元模型中很难有效进行;Zhang等提出了用正交表法估计异方差线性回归模型[4],此方法将广义最小二乘和正交表法结合起来,模型估计结果具有一定的可靠性,但在用正交表法估计模型误差项估计量的过程中,产生因变量值时未用到自变量的信息,因此该方法在精确性上有待改进;张荷观提出了用分组两阶段估计方法对异方差线性回归模型参数进行估计[5],此方法不受模型维数的限制,是通过分组的方法对自变量产生重复数据进而对模型进行估计,但这有可能造成样本信息的损失,而且在多元线性回归模型中此方法需要先判断引起异方差最主要的自变量,而如何判断引起异方差最主要的自变量目前还没有比较有效的方法,因此分组两阶段估计方法具有一定的局限性;李顺勇等提出了基于变量选择和聚类分析的两阶段异方差模型估计[6],此方法把变量选择和聚类方法与广义最小二乘法结合起来,使模型估计具有一定的可行性,但在样本较小的情况下使用聚类方法容易聚成单类情况,此时这种方法失效,因此该方法也有一定的缺陷。基于上述分析,本文拟提出一种新的异方差模型的两阶段估计,主要思想是把异方差一致协方差阵估计HC5m和广义最小二乘估计法相结合,综合使用样本的全部信息,而且不受模型维数的限制,并将通过大量蒙特卡洛数值模拟和实证研究,对该方法和分组两阶段估计方法进行比较分析。
二、基本知识
(一)异方差模型
经典线性回归模型一般形式为:
(1)
用矩阵表示为:
(2)
其中
(二)分组两阶段估计
当异方差模型的误差项的协方差阵未知时,张荷观使用分组两阶段估计方法对异方差模型进行估计。以式(1)为例,介绍此方法的主要思想和步骤。假设样本数据(yi,xi1,xi2,…,xip),i=1,2,…,n满足式(1),x(1)=(x11,x21,…,xn1)T是引起线性回归模型异方差最主要的自变量,该方法的主要思想和步骤如下:
1.把自变量x(1)的观测值x11,x21,…,xn1按由小到大进行排序,其它自变量和因变量与之原对应的关系保持不变。

(3)
对式(3)两边同时除以στ,则式(3)变成同方差线性回归模型。
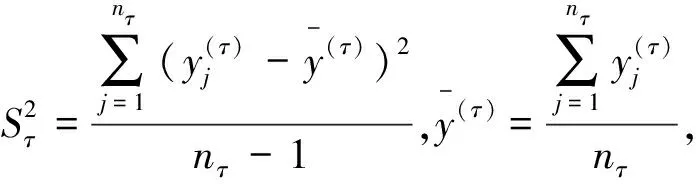
5.把στ的估计量Sτ带到变换后的式(3)中,根据OLS法求出模型估计即为式(1)的估计。
(三)异方差一致协方差矩阵估计
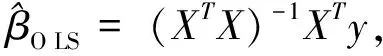
1980年,White提出了异方差一致协方差矩阵估计量(HCCME)[7],该估计量称为HC0:

在同方差和异方差的模型中,当误差项的协方差矩阵形式未知的情况下,HC0估计是协方差阵Ψ的一致估计量,因此根据HC0估计进行模型的显著性检验和回归参数的显著性检验,但HC0估计只适用于大样本情况下,当样本量比较小时则会产生较大偏差。实际上,HC0低估了模型参数估计的真实方差,使得quasi-t检验不再具有一定的精确性,一些学者对HC0估计量做了一些修正,这些修正方法统称HCCMEs[8-13],包括:
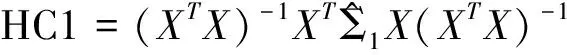


ω=1,2,3,4,5,4m,5m,hi为帽子矩阵H的第i个主对角元素,i=1,2,…,n,及
i=1,2,…,n。且
三、异方差模型的两阶段估计—基于异方差一致协方差阵估计
张荷观在两阶段估计方法中使用了分组方法使自变量产生重复数据,这有可能损失样本信息,而且在多元线性回归模型中进行异方差检验时采取把多元线性回归模型的异方差检验变为对每个一元线性回归模型进行Cochran异方差检验。若所有一元线性回归模型均不存在异方差,则可说明多元线性回归模型不存在异方差(反之亦然),再比较存在异方差的一元线性回归模型的Cochran检验临界值大小,由最大的Cochran检验临界值作为引起多元线性回归模型异方差最主要的自变量;由于多元线性回归模型并不等同于多个一元线性回归模型的简单相加,一般情况下会有多个自变量使模型出现异方差,因此使用分组两阶段估计方法对多元线性回归模型进行估计的结果也就不具有一定的精确性。针对分组两阶段估计方法的局限性,本文提出了异方差线性回归模型的两阶段估计,即基于异方差一致协方差阵估计。
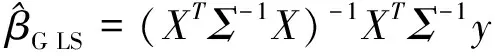
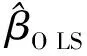

综合上述思想,下面给出该方法的具体步骤:
第一步,由异方差一致协方差矩阵估计量HC5m计算Σ5m,作为异方差线性回归模型误差项协方差阵Σ的估计。

本文将在一元和多元异方差线性回归模型下,用大量数值模拟和实证分析比较本文提出的方法(简记为M1)与分组两阶段法(简记为M2)的优劣,并选用如下三个衡量指标进行评价:
模型误差项方差的平均绝对误差[注]此评价指标进行的是横向比较,即在相同的情况下不同方法间的优劣比较。:
模型因变量预测值的平均绝对误差[注]同上。:
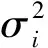
决定系数R2:
四、数值模拟和实证分析
(一)数值模拟
本节数值模拟部分的r模拟重复次数为1 000次,其中M2的分组组数k的取值分别为3、6、10。
1.一元异方差线性回归模型的数值模拟
假设一元异方差线性回归模型为:
yi=β0+β1xi+εi(i=1,2,…,n)
(4)
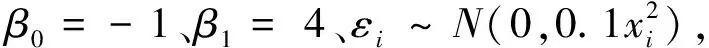
在表1中的任何一种情况下,使用M1得出的参数估计值均非常接近真实值-1和4;而使用M2在x~P(6)、k=3情形下,估计值与设定值相差较大,说明在一元异方差模型中M1在模型的估计和拟合精度方面更具有一定的优势,原因在于M1综合使用了全部的样本信息。从图1可见,在不同样本量下使用M1得出的MAEΣ和MAEy均小于使用M2得出的结果,而使用M1得出的R2均大于用M2得出的结果。

图1 在x~U(0,10)下MAE∑,MAEy、R2模拟结果比较图

自变量的取值分布样本量参数估计M1M2k=3k=6k=10x~U(0,10)n=30n=60n=90^β=^β0^β1()-1.015 44.005 2()-1.118 44.013 1()-0.974 93.989 9()-1.000 53.996 9()-1.006 84.001 8()-0.988 13.996 3()-0.967 43.987 9()-1.006 73.995 6()-0.996 13.998 1()-0.998 53.995 3()-0.983 93.992 9()-1.006 53.996 5()x~U(0,5)n=30n=60n=90^β=^β0^β1()-1.003 34.006 7()-0.982 94.379 8()-0.999 54.051 5()-0.998 53.994 8()-0.999 93.999 6()-0.988 84.445 2()-1.001 34.092 5()-0.998 64.0159()-1.001 74.001 6()-1.020 54.459 5()-0.999 74.101 4()-0.998 34.028 0()x~P(6)n=30n=60n=90^β=^β0^β1()-0.990 23.998 0()-2.878 84.330.3()-1.188 24.025 9()-0.927 33.989 0()-1.014 74.003 6()-3.434 14.435 6()-1.425 84.077 9()-1.115 14.019 3()-1.010 04.002 0()-3.581 34.436 8()-1.358 94.082 2()-0.993 93.996 9()
2.多元异方差线性回归模型模拟
假设多元异方差线性回归模型为:
yi=β0+β1xi1+β2xi2+β3xi3+εi
i=1,2,…,n
(5)
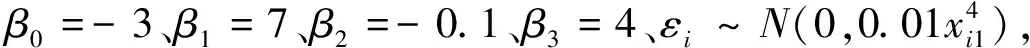
1)x1,x2,x3~U(0,10)
2)x1,x2,x3~N(10)
3)x1,x2,x3~Exp(1)
4)x1~U(0,10)x2~Exp(5)x3~P(3)
即样本量n的取值和自变量x的取值分布共有12种组合。通过式(5)可以得到n个因变量y的样本观测值,分别用M1、M2对式(5)的参数进行估计,部分模拟结果如表2和图2所示。
表2是在x1,x2,x3~Exp(1)与x1~U(0,10)、x2~Exp(5)、x3~P(3)情形下,使用M1、M2在不同的样本量下模型参数估计的模拟结果;图2是在x1~U(0,10)、x2~Exp(5)、x3~P(3)情形下,使用M1、M2在不同的样本量下得出的MAEΣ、MAEy、R2的结果比较。

表2 多元线性模型参数估计模拟结果表

图2 在x1~U(0,10)、x2~Exp(5)、x3~P(3)下MAEΣ、MAEy、R2的模拟结果比较图
由表2可见,各种情形下的参数估计值均非常接近真实值-3、7、-0.1、4,但在多数情况下使用M2得出的参数估计值与真实值的偏离程度都比较大,这说明在多元异方差线性回归模型中,M1在模型的估计和拟合精度方面同样更具有一定的优势,原因同样在于M1综合使用了全部的样本信息。
从图2可见,在不同的样本量下使用M1得出的MAEΣ、MAEy均小于使用M2得出的结果,使用M1得出的R2值均大于使用M2得出的结果;且M2方法的MAEΣ,MAEy值有随样本量的上升而下降的趋势,而本文提出的M1方法的MAEΣ,MAEy值基本随样本量的上升而上升的趋势,这种情况的产生有以下两个原因:
第一,对MAEΣ,MAEy进行的是横向间比较,即在相同情况下对不同方法间的优劣比较,图2主要是为了更直观地说明两种方法M1与M2间的优劣;MAEΣ、MAEy实际上并不能很恰当地反应出每种方法间的纵向比较(也没有必要),即在不同的样本量下MAEΣ、MAEy值的大小比较没有直观的意义。
第二,从图2可见,M2方法的MAEΣ、MAEy值虽然有随样本量的上升而下降的趋势,但每种情况的变化幅度均较大;而M1方法的MAEΣ、MAEy虽然有随样本量的上升而上升的趋势,但是均在同一个数量级下变化且变化的幅度比较小,说明M1方法比较稳定,并且结果均小于M2方法的MAEΣ、MAEy的值。
(二)实证分析
本文实证分析分为一元和多元异方差线性回归模型两部分。为了更方便地比较M1与M2之间的优劣,两部分实证数据均使用张荷观的数据。
1.一元异方差线性回归模型实证分析。本数据是关于40户家庭收入x(美元)与消费支出y(美元)的数据,建立线性回归模型如下:
yi=β0+β1xi+εi(i=1,2,…,40)
(6)
经检验模型(6)存在异方差,使用M1、M2方法对模型(6)进行参数估计的结果见表4。

表4 一元异方差线性回归模型估计实证分析结果表
从表4可以看出:使用M1得出的MAEy小于用M2得出的结果;除了在k=10情况下,使用M2得出的R2与用M1得出的R2非常接近外,其它情况均明显小于用M1得出的结果;在模型参数估计方面,使用M1和M2得出的参数估计值符号均一致。综上,在一元异方差线性回归模型实证分析中M1比M2好。
2.多元异方差线性回归模型实证分析。本数据是关于31个地区城镇居民家庭消费性支出y与收入x1、食品支出x2及娱乐教育文化服务支出x3的数据,建立线性回归模型如下:
yi=β0+β1xi1+β2xi2+β3xi3+εi
i=1,2,…,31
(7)
其中根据张荷观提出的异方差检验法,模型(7)存在异方差,而且自变量x1是引起异方差的最主要因素。使用M1,M2对模型(7)的估计结果如表5所示。
从表5可以看出:使用M1得出的MAEy小于用M2得出的结果,用M1得出的R2大于M2得出的结果;在模型参数估计方面,使用M1得出的估计值除了常数项符号与用M2得出的相反外,其它模型系数估计值符号均一致,而常数项符号并不影响模型的精确性。由此得出,在多元异方差线性回归模型实证分析中M1比M2好。

表5 多元异方差线性回归模型估计实证分析结果表
五、结 论
本文将异方差一致协方差阵估计HC5m和广义最小二乘估计法相结合,综合使用全部样本的信息,提出了一种新的异方差模型估计方法M1,改进了原有的两阶段估计方法M2。通过对一元和多元异方差线性回归模型分别用M1、M2进行数值模拟,结果表明M1优于M2;同时,对一元和多元异方差线性回归模型分别在M1、M2下进行实证分析,结果同样表明M1比M2效果好。可见,本文提出的方法不受模型维数限制,不会造成样本信息的损失,对模型的拟合更加精确。
本文讨论的是假定误差项的协方差矩阵为对角矩阵的情形,但在实际中还存在一些线性回归模型误差项的协方差阵形式更一般的情形(不是对角阵),而且误差项的协方差阵里常常包含着未知参数。目前,对未知参数的估计还没有确定的估计方法,因此笔者认为在这方面还有必要做进一步的探索性研究。

