基于改进Gini-Simpson指数的指标及权重均为混合属性的广义灰靶决策方法
马金山
(河南理工大学 能源科学与工程学院,河南 焦作 454000)
一、引 言
自邓聚龙教授提出灰靶决策方法以来,许多学者对其进行了研究改进[1]171-209。随着决策理论与方法研究的深入,决策方案的指标值也由单纯的实数值拓展为混合属性指标值。混合属性灰靶决策方法也随之产生,进一步增强了该方法的适用性。灰靶决策方法的核心是求各决策方案对于靶心的靶心距,并以靶心距作为各方案优劣决策的依据。决策方案指标值为确定性实数的灰靶决策方法,其对靶心距的获取主要采用距离法,如采用欧氏距离法或马氏距离法等[2]。包含确定数和不确定数的混属性灰靶决策方法对靶心距的获取方法:一类是采用距离的方法进行处理,主要是采用欧氏距离[3-4];另一类是采用变形方法如采用蛛网面积和关联系数求靶心距[5-6];还有一类是采用向量的方法进行处理,这称为混合属性广义灰靶决策方法[7-8]。广义灰靶决策方法是基于传统的灰靶决策方法,在遵循其基本原理不变的基础上提出的一种方法,基本的计算过程与传统方法有所不同[7-9]。由于混合属性灰靶决策中涉及不确定性的属性值,需要融入能够测度这种不确定性的理论方法来进行方案的决策更具有理论意义和实际的应用价值。意大利统计学家Gini首次提出了不均等指数及其算法,称为基尼指数(Gini index)。该指数是一个定量测定收入分配差异程度的指标[10]。随着研究的深入,基尼指数已经不局限于度量收入分配的不均衡,而有了更深入的改进和应用。基尼系数有许多表现形式,近年来其重要的形式Gini-Simpson指数得到了重视和应用[11-13]。Gini-Simpson指数主要应用于生物多样性的检测等方面[11-12]。另外该方法在医学病毒检测方面的应用也获得了理想的效果[14]。同时,Gini-Simpson指数还被用于不确定性的测度方面[15-17]。鉴于Gini-Simpson指数能够测度信息的不确定性,所以可以将其用于涉及不确定数的混合属性广义灰靶决策中。
二、基本理论
(一)不确定数及区间数
由于客观事物的复杂性和不确定性以及人类的知识局限性和认识能力的模糊性,人们对事物的认识常常具有不确定性,而描述这些事物特征的数据则称为不确定数。在实际的应用中,由于测量、计算所带来的数据误差,以及信息不完全带来的数据缺乏,表示特征行为的原始数据往往会是一个范围,为此下面给出区间数及其拓展的n参数区间数(多参数区间数)的定义。


本文在不引起歧义的情况下,区间数有时也包含n参数区间数(多参数区间数),而本文所称的不确定数主要指的是区间数及其拓展的多参数区间数。
(二)二元联系数
定义2记R为实数域,称A+Bi为二元联系数,其中A,B∈R,i∈[-1,1],A表示确定的项,B表示不确定的项,i是一个变动的项,它的存在统一了不确定数的确定和不确定性。


(1)

(2)
(3)
(4)
v=min{η,θ}
(5)
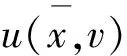
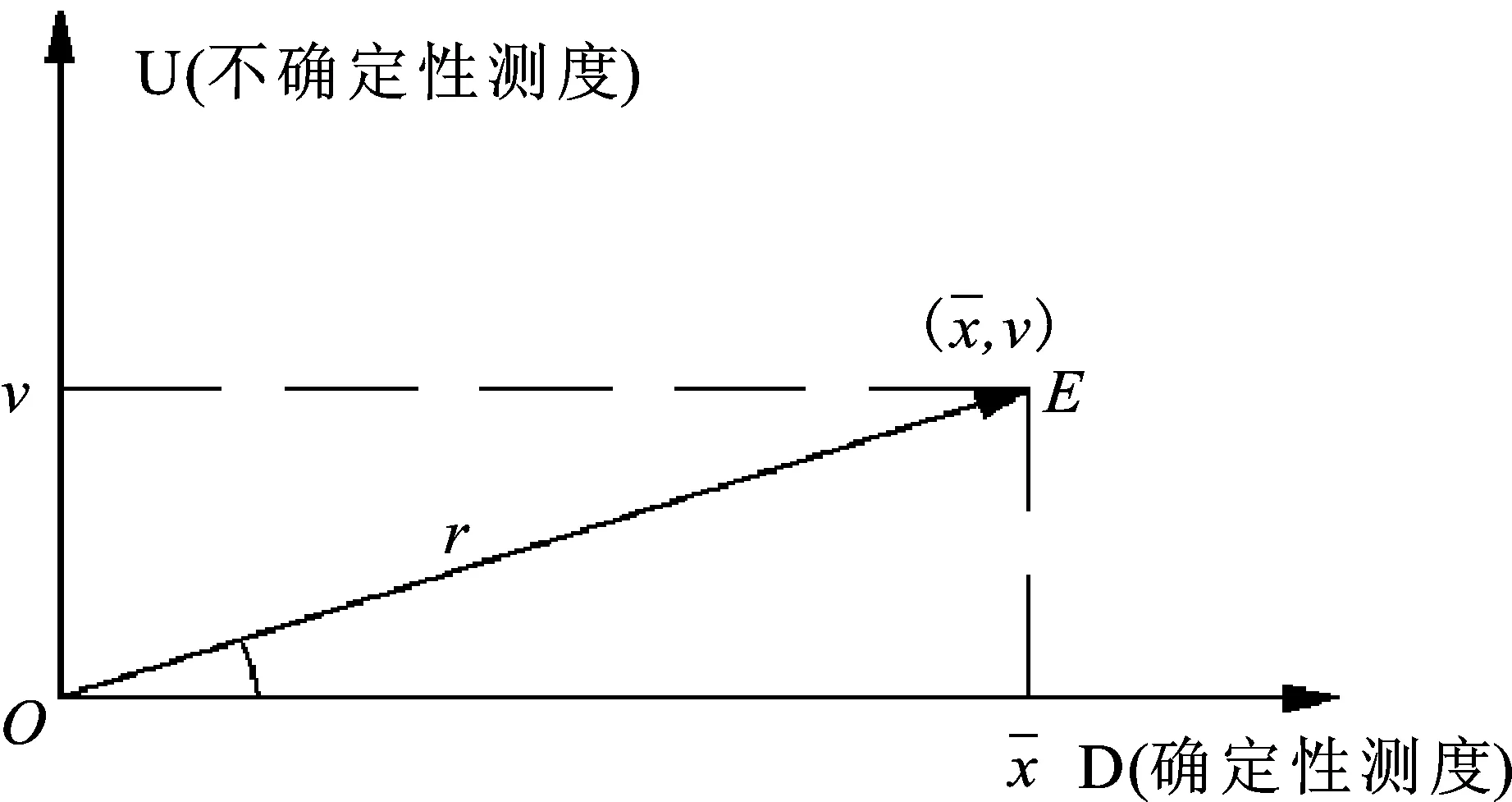
图1 确定-不确定空间
(三)Gini-Simpson指数
定义5Gini-Simpson指数。对于概率分布P=(p1,p2,…,pm),其Gini-Simpson指数定义为[12-13]:
(6)
其中pj为对应的某一变量的概率。
定义6综合加权Gini-Simpson指数。设S=((x1,y1),(x2,y2),…,(xm,ym))Τ为在多属性灰靶决策中某方案指标的(确定度,不确定度)二元组数向量,E=((p1,q1),(p2,q2),…,(pm,qm))T为靶心的(确定度,不确定度)二元组向量,且S和E已经过了规范化处理,其属性权重向量为W=(w1,w2,…,wm)Τ,则其综合加权Gini-Simpson指数为:
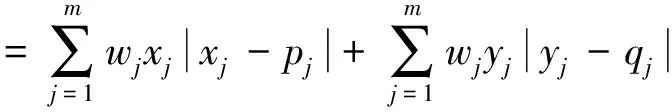
(7)
与式(6)不同,式(7)包含了针对各方案指标的(确定度,不确定度)二元组数与靶心指标的(确定度,不确定度)二元组数的相互联系,即由式(7)中的|xj-pj|和|yj-qj|予以体现,表示的是各方案指标与靶心指标的相似性程度。即改进后的综合加权Gini-Simpson指数既体现各自指标的差异又反映了与靶心指标的相似性。
三、基于Gini-Simpson指数的混合属性广义灰靶决策方法
(一)决策的基本原理
基于改进Gini-Simpson指数的指标及权重均为混合属性的广义灰靶决策方法,其基本原理是:首先,将决策方案的各指标均转换为可以统一度量的二元联系数;其次,将各指标的二元联系数分解为(确定,不确定)二元组数,并据此求出各属性靶心指标的(确定,不确定)二元组数;然后,对方案指标和靶心指标的(确定度,不确定度)二元组数进行规范化处理,采用权重函数将各混合属性指标权重确定化;最后,求得各方案的综合加权Gini-Simpson指数,以其值越小方案越优。
该决策方法有如下关键点:一是采用二元联系数作为基本的工具,将各类不同的数据如实数和区间数(包括多参数区间数)等统一转换为包含了确定和不确定性的二元联系数便于随后的统一处理;二是将靶心指标与对应的各方案指标归一化后的(确定度,不确定度)二元组数建立联系,此处是确定靶心指标与对应的各方案指标接近性或同一性的重要依据;三是构造混合属性指标权重确定化方法,将不确定性混合指标权重确定化。
(二)基本决策要素的处理
设有方案集T={T1,T2,…,Tn},属性集A={A1,A2,…,Am},则方案Ts在属性At下的指标值记为vst(s=1,2,…,n;t=1,2,…,m),其属性权重向量为W=(w1,w2,…,wm)T。
1.方案指标均转化为二元联系数
采用式(1)~(5)将不同类型的数据转换为二元A+Bi的联系数形式,其中实数认为是二元联系数中的确定项为该数值本身,不确定项为0,即为A+0i的形式。设转化后的各指标联系数为Vst=Ast+Bsti(s=1,2,…,n;t=1,2,…,m)。
2.各指标属性的靶心指标二元组数的获取

(8)
式(8)为求某一指标属性靶心的(确定,不确定)二元组数,注意此处所求出的(确定,不确定)二元组数为未事先进行规范化的二元组数。当其为正向指标时,分别取该属性下的最大确定项及最小的不确定项为该属性下的靶心二元组数;当其为逆向指标时,分别取该属性下的最小确定项及最小不确定项为该属性下的靶心二元组数。
3.各决策方案指标值的归一化处理
已得到各属性下各方案的指标联系数Vst(s=1,2,…,n;t=1,2,…,m)及靶心的指标联系数Vct(c=n+1;t=1,2,…,m),则可以将其表示为由确定度和不确定度组成的二元组数向量。
(9)
式(9)中ast,bst分别代表对应的某一属性下各指标标准化后的二元联系数的确定度和不确定度。为此,可以组成各方案的二元组数向量为((as1,bs1),(as2,bs2),…,(asm,bsm))T。但此处需要说明的是针对实数的情况,由于不确定性部分为0,所以首先不能对其进行规范化处理,否则某一属性下的实数值的确定性部分会全部相同,导致计算过程出现错误。
前面所求出的各方案的指标向量与靶心指标向量的(确定度,不确定度)二元组数是不同的,属性之间不具有可比性,因此这里需要针对各个属性下的(确定度,不确定度)二元组数中的元素ast和bst进行归一化,计算见式(10)。
s=1,2,…,n;t=1,2,…,m
(10)

4.混合属性指标权重的确定化方法
混合属性指标权重值wt(t=1,2,…,m)包含了不确定性的内容,其可以为实数或不确定数,当其取值为不确定数时,可为区间数、3参数区间数或者4参数区间数形式,即有:
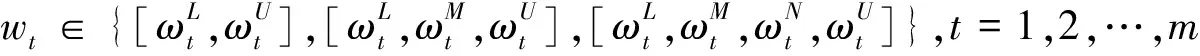
(11)
此时一般有下面的关系式成立:
(12)

指标权重为混合属性值时确定化的步骤如下:
(1)将各属性权重值转化为二元联系数
首先采用式(2)~(5)计算各类型权重值的基本参数包括均值、标准差以及极差值。然后将各类型数据表示的权重转化为二元联系数的形式见式(1),并且分别组成(确定,不确定)二元组数。以二元组数构成的权重向量为((a1,b1),(a2,b2),…,(am,bm))Τ。
(2)求权重(确定,不确定)二元组数的基准值
根据权重的(确定,不确定)二元组数,求出各二元组数中确定项的最大值和不确定项的最小值,即采用式(13)。
w0=(max{aj},min{bj}),j=1,2,…,m
(13)
由式(13)可以得到权重确定的基准二元组数为(amax,bmin),amax和bmin分别代表选出的(确定,不确定)二元组数中,确定性最大的项及不确定性最小的项。值得注意的是此处的bmin为除0以外的其它的不确定项的最小值。
(3)构造不确定性权重确定化的函数
不确定性权重确定化既要包含确定性因素对权重的影响,也要考虑不确定性部分对权重的影响,其权重函数见式(14)。
j=1,2,…,m
(14)
其中,αj为求权重wj时(确定,不确定)二元组数中确定项所贡献的比例;βj为不确定项所贡献的比例;bmin为除0以外最小的不确定项的取值。公式(14)表示,当bj≠0时,某指标确定性的权重与其(确定,不确定)二元组数中确定性部分和不确定性部分相关;当若权重指标(确定,不确定)二元组数为(aj,0)的形式时则wj只取决于确定性部分。
式(14)中,虽然αj的取值可以根据决策者的偏好来决定,但考虑到不确定数自身所包含的信息,所以对式(14)进行参数的赋值修正见式(15)。
wj=
j=1,2,…,m
(15)
(4)拟采用权重的归一化处理
步骤(3)所求出的各指标属性的权重值wj未经规范化,与通常意义上的各指标属性权重值的和为1有所差异。为此,对步骤(3)求出的权重数据参考式(10)进行线性归一化处理,得到通常意义下的权重值。
(三)决策步骤
基于改进的综合加权Gini-Simpson指数的混合属性广义灰靶决策方法决策步骤如下:
(1)所有方案指标依据式(1)~(5)转化为二元联系数,并分别组成为(确定,不确定)二元组数。
(2)采用式(8)求各属性下的靶心指标的(确定,不确定)二元组数。
(3)将各指标及靶心的(确定,不确定)二元组数运用式(9)进行标准化,然后对在各属性下的(确定度,不确定度)二元组数采用式(10)进行线性归一化处理。
(4)采用式(13)及(15)获得各决策方案指标属性的确定性权重。
(5)采用式(7)求得各方案的综合加权Gini-Simpson指数,根据所获得的Gini-Simpson指数对各决策方案进行决策,以其值越小方案越优。
四、案例分析
(一)数据来源
对战术导弹进行评估,采用6个指标分别是命中精度(km)、弹头载荷(kg)、机动性能(km·h-1)、价格(106g)、可靠性和可维护性,分别用A1~A6表示[7]。其中A1和A4为成本型指标,其余为效益型指标。其中各个指标的权重为W=([0.16 0.18
0.2],[0.18 0.2 0.22],0.1,[0.18 0.2 0.22
0.24],[0.14 0.18],[0.12 0.16])。4个方案分别用T1~T4表示,数据见表1所示。

表1 各方案的指标值
(二)决策过程
(1)计算决策方案指标的二元联系数参数。由表1中数据采用式(1)~(5)可以求出各指标的用于二元联系数计算的参数见表2。

表2 各方案指标参数的均值、标准差和最大偏差
注:表中的“a/b/c代表“均值/标准差/最大偏差”。
(2)将所有方案的指标均转化为二元联系数。根据式(1)~(5),基于表2数据将表1所示的各指标值转化为联系数的形式见表3。然后对表3的二元联系数形式转化为(确定,不确定)二元组数的形式,见表4所示。

表3 转化后的各指标二元联系数

表4 转化后的各指标二元组数
(3)求各指标属性靶心的二元组数。采用式(8)求得各属性的靶心的二元组数向量为:((1.8,0),(540,0),(55.5,0.5),(4.7,0.5),(0.7,0.1),(0.9,0.1))。
(4)对各方案及靶心确定度及不确定度二元组数进行规范化。首先对表4的各方案指标及靶心指标二元组数采用式(9)进行规范化,然后采用式(10)再对其二元组数进行归一化处理后见表5。

表5 各方案及靶心的规范化二元组数
(5)不确定性权重的确定化。已经给定各个指标的混合属性权重W=([0.16 0.18 0.2],[0.18 0.2 0.22],0.1,[0.18 0.2 0.22 0.24],[0.14 0.18],[0.12 0.16]),其中以不确定数表示的权重数据的参数下限值为小于或等于1,而上限值为大于或等于1。首先,采用式(1)~(5)计算各个混合数据类型权重的参数见表6;其次,将各权重表示为二元联系数向量的形式见表7。

表6 所有指标权重参数的均值、标准差和最大偏差

表7 指标权重的二元联系数
采用式(13)计算得到权重(确定,不确定)二元组数的基准二元组数为(0.21,0.02)。然后采用式(15)计算得到确定化的权重为(2.644 2,2.849 5,1.609 9,2.962 7,2.463 0,2.312 6)。最后进行线性归一化后得到的权重为W=(0.178 0,0.192 0,0.108 5,0.199 6,0.166 0,0.155 8)。
(6)求各方案与靶心综合加权Gini-Simpson指数。给定确定化后的权重W=(0.178 0,0.192 0,0.108 5,0.199 6,0.166 0,0.155 8),采用式(7)计算得到各方案的综合加权Gini-Simpson指数为ICWGS=(0.006 0,0.037 8,0.011 8,0.024 7)。根据综合加权Gini-Simpson指数越小越优的决策原则,可以得到各方案的优劣排序为T1≻T3≻T4≻T2。
(三)分析讨论
为了说明该方法的可行性和有效性,此处与Ma的以向量接近度为决策依据的方法进行对比[7],同样采用权重W=(0.178 0,0.192 0,0.108 5,0.199 6,0.166 0,0.155 8)时,可得到各方案综合加权的接近度为:ICWP=(0.195 5,0.303 0,0.227 0,0.274 4)。根据综合接近度越小方案越优的原则,可以得到各决策方案的排序为:T1≻T3≻T4≻T2。表8为两种不同方法计算结果的对比。

表8 两种决策方法的计算结果对比
以上两种不同方法决策结果的对比分析,说明所提出的决策方法决策结果与以向量接近度为依据的方法相比决策结果完全一致,决策的效果较好。两种决策方法的相同点为:均是将各类不同的数据统一转化为包含确定和不确定性的可统一处理的二元联系数,即二元联系数为各类不同数据统一转化的工具。两种决策方法的不同点为:本文的方法是采用基于改进综合加权Gini-Simpson 指数的方法作为决策的依据,是从方案的不确定性度量的视角进行决策;而文献[7]中的方法则是采用以向量为基础的接近度为基础作为决策的依据,是从方案的向量接近性或相似性视角进行决策。
总之,案例分析的结果表明,本文的方法与已有的以向量接近度为基础的方法相比决策结果符合性很好。不同于以向量的接近性或相似性为视角的混合属性广义灰靶决策方法的决策思路,该方法解决问题的视角是以方案的不确定性度量为基础的。

