免疫遗传神经网络算法的纱线原料性能反演

查刘根 谢春萍

(江南大学，江苏无锡 ，214122)

纱线生产加工过程中，其质量的优劣不仅取决于生产加工工艺、工人的技术水平以及机械设备的性能，更是与原棉质量的优劣及不同批次原棉的搭配使用情况存在着密不可分的联系[1-3]。纱线质量预测问题的一个重要的研究方向是科学地分析纱线产品质量与原棉性能之间存在的必然联系，建立最为逼近的数学模型，最大程度地利用各批原棉自身的优良性能，从而起到稳定生产，节约成本的作用[4-5]。

纱线质量预测模型是一种非线性优化模型，可通过非线性函数来表达，其反演模型解决的也是一种非线性最优化问题，可用于指导配棉[6]。正演模型中输出的纱线质量参数是确定的，而其中一个或多个输入的原棉性能参数可通过构造的反演模型获得多组不同的组合，然后综合考虑生产成本和产品要求选出最优的参数组合，从而可设计出更加合理的配棉方案。近年来，国内外广泛使用BP神经网络和遗传算法等全局优化算法处理反演问题。文献[7]提出了一种修改的非线性共梯度算法，该方法主要利用IRLS(Iterative Reweighted Least Square )算法的加权思想来改变搜索方向从而增加稳定性。文献[8]采用直接逼近法来反演棉花模型所需的初始数据及参数，将遥感信息和棉花模型相结合，建立遥感-棉花的反演模型，试验验证了该模型是可行的。针对传统参数反演算法存在收敛性和稳定性不理想、反演精度较低、计算速度较缓慢，以及标准遗传算法存在的早熟收敛等问题，本文利用免疫遗传算法优化BP神经网络的权值和阈值来建立遗传神经网络正演模型，根据纱线强力值来反演原棉性能的输入参数，研究结果可为纺织企业的配棉工作提供可靠的理论依据。

1 模型简介与参数选择

本文选取纱线质量预测模型作为研究对象，主要考虑到以下几个方面的因素：首先,它是一个经过大量试验数据验证并在实际中得到应用的一个模型；其次, 模型是动态和非线性的，参数之间具有较强的相互作用；最后，模型的结构相对比较简单，参数之间的关系容易把握。

纱线的生产加工，其产品的质量与原料的性能及工艺参数的设定紧密相关。理论上讲，预测的纱线质量参数不同，选取的原料性能参数和生产工艺参数均不同。但是，反演参数设定过多，就会降低优化的准确性，延长优化时间，所以，本文的反演参数的选择主要考虑变化范围较大的，模型比较敏感的若干原料性能参数[9]。当输出的纱线质量参数确定后，通过反演模型去寻找满足实际生产需要的原料性能参数组合，再综合考虑原料成本与产品质量要求等条件筛选出最佳组合参数，从而设计出更加合理的配棉方案。

2 反演模型的数学表述

因为在纱线原料性能参数的反演问题中，误差泛函是复杂的多峰函数，所以这里需要构建的是一种全局寻优反演模型。将参数反演抽象为数学模型，描述如下。

(1)设Y是纱线的某一重要性能参数，{p1,p2,…,pn}是此纱线的部分原料性能参数，Y={p1,p2,…,pn}，即Y的值可由集合{p1,p2,…,pn}中的参数预测得出。

(2)假设pi和pj是两个重要的原棉参数，现需要为某一配棉方案确定更多的组合以供选择，也就要反演获得更多的参数pi和pj。通过构建神经网络，以一组{p1,p2,…,pn}为输入参数，以参数Y作为网络的输出，然后将通过训练得到的网络封装成一个函数，f(p1,p2,…,pn)，即对任意的{p1,p2,…pi…pj…,pn}集合，都可以由函数f计算求得Y。

(3)构造免疫遗传算法，将pi和pj编码成染色体。正演模型的误差可表示为：

E(p1,p2,…,pn)=f(p1,p2,…,pn)-Y真实值

(1)

则反演模型的目标函数(适应度函数)可表示为：

F(p)= min{abs[E(p1,p2,…pi…pj…,pn)]}

(2)

从而得到反演参数pi和pj。

3 反演算法设计

3.1 反演的基本步骤

反演算法的流程图如图1所示。

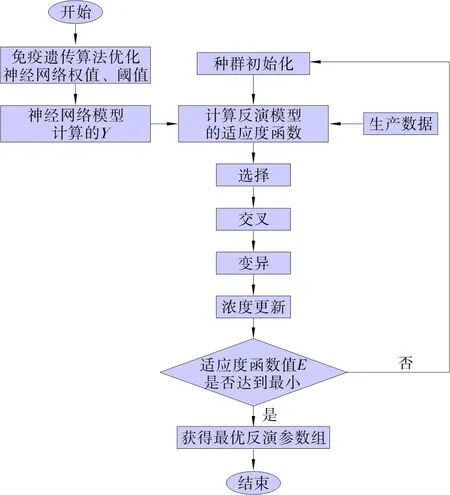
图1 反演算法流程图

(1)基于已知纯棉纱线纤维样本的马克隆值、上半部平均长度、整齐度、短纤维指数和单纤维强度等条件，结合免疫遗传算法和神经网络算法建立针对初始纱线强力值的预测模型。

(2)根据建立的初始纱线强力值预测模型得到预测结果，可以得到实际数据与计算数据的均方根误差，若满足精度要求则迭代结束，否则继续迭代直至精度符合要求。

(3)基于当前正演模型，通过免疫遗传算法构造其反演模型，用来反演原料性能参数。

(4)以纱线强力值实测数据与预测数据的差作为适应度函数的值，通过迭代寻优，得到最佳性能参数组合。

(5)根据正演模型计算纱线强力值预测数据，从而得到目标函数值，根据目标函数值的精确度得到最合适的原料性能参数。

3.2 免疫遗传算法的BP神经网络设计

3.2.1 BP神经网络建模

本文构造的单纱强力预测模型所使用的数据来源于山东某棉纺织厂的原棉物理指标及细纱质量指标，为提高预测结果的准确性和计算的稳定性，数据在使用之前使用log函数进行了统一的归一化处理。网络以马克隆值、上半部平均长度、整齐度、短纤维指数和强度作为输入，以纱线强力值为输出，即输入层有m=5个神经元，输出层有n=1个神经元，隐含层单元数可由经验公式(3)[10]得到s=4，最后，得到的三层BP神经网络的拓扑结构如图2所示。

s=

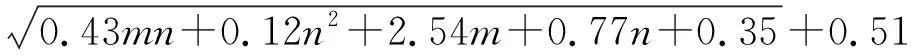
(3)

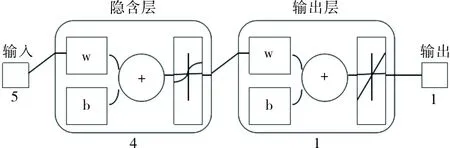
图2 3层网络结构

3.2.2 网络权值和阈值的优化设计

(1)编码：将待寻优变量即神经网络的连接权值和阈值作为抗体进行编码，考虑到单独的二进制编码的复杂性以及计算量大的缺点，本文主要采用实数编码，在基于浓度的群体更新时再转换成二进制进行操作，可有效提高算法的收敛速度。

(2)初始群体的产生：随机化生成M个抗体组成初始种群。设输入单元数为m，隐层单元数为n，输出单元数为l，则连接权值共有m×n+n×l个，阈值共有n+l个，抗体长度为L=m×n+n×l+n+l。

(3)适应度函数的设计：对于给定的训练数据与实际数据，将实际数据与预测数据的平均绝对误差E定义为BP神经网络的目标函数F(x)=minE，而免疫遗传算法解决的一般是目标最大化问题，故最终的适应度函数设定为Fitness(x)=1/F(x)。

(4)遗传操作。

选择：采用适应度比例的方法选择子代抗体，设M为抗体数量，fj是第j个抗体的适应度值，那么该抗体被选择的概率为pj，适应度比例法很好地保留下了高适应度的父代抗体，保证优良基因逐代遗传，有效地维持了算法的全局搜索能力。

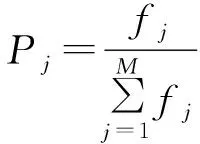
(4)

交叉：本文采用算数交叉法，通过设定一个参数α和线性重组可以产生任意两个位于两个父代抗体间的子代抗体。

变异：变异操作能恢复抗体失去的或未开发的有效信息，维持群体的多样性，本文采用单重均匀变异法。

(5)基于浓度的群体更新：如果只是通过简单的遗传选择筛选出大量的高适应度父代抗体，而不施加控制，那么这些个体的浓度就会越来越高，收敛后期群体的多样性便会急剧降低，最终算法陷入局部极值。所以，就需要找到一个更好的方法，既能保留住高适应的个体，还可以确保在新产生的抗体群里，适应度值较低但可能包含优良基因的个体也有被挑选出来的机会，这就是基于浓度机制的群体更新，该操作能够维持每代抗体群的多样性。

在这里先给出信息熵、相似度和抗体浓度的概念和计算公式。

信息熵:免疫系统中，一个抗体所包含的信息量可由香农的平均信息熵H(M)来表述。设某抗体包含S种不同的符号，某一符号位于t号基因座的概率pst可由式(5)计算得出，即：

(5)

则Ht(M)为第t基因的信息熵，定义为：

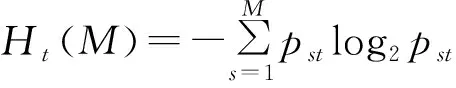
(6)

整个群体的平均信息熵为

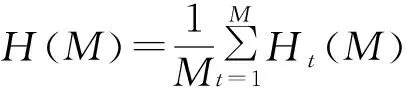
(7)

相似度：抗体a和抗体c相似的程度称之为它们的相似度。

(8)

H(2)可由式(7)计算得出，是两个抗体的平均信息熵。还可以定义群体的相似度X(M)：

(9)

X(M)的大小反映了整个群体的相似程度，X(M)∈(0，1)，X(M)越大，群体相似度越高，当X(M)=1时，表示所有抗体完全相同的。

抗体浓度：抗体浓度是指某个抗体和与其相似的个体在种群中的比率，可由公式(10)[11]求得，其中，σ为相似度常数，一般取0.9～1。

(10)

伴随着抗体群的不断更新，部分抗体的相似度必定会逐渐增大，为了有效地保持群体的多样性，为其相似度设定一个阈值(设为X0，X0与抗体群规模的大小呈正比)，当群体发展到其相似度大于该阈值时，就将随机增殖Z个新抗体，抗体总数扩大为M+Z。

在单一适应度评价方法之上，加入抗体浓度进行调整，提出聚合适应度的概念，作为最后筛选个体的评价指标，其表达式如式(11)[12]所示，其中，对于本文的最大优化问题，β应为负数，取β= -0.6。

聚合适应度=适应度×exp(β×Ca)

(11)

采用聚合适应度比例的方法更新下一代群体，某抗体被保留下来的几率与其聚合适应度呈正相关，最终筛选出M个抗体作为下一代的种群。这种做法的优点在于，一方面抗体的浓度不变时，聚合适应度的大小与适应度的值呈正相关，能够有效保留住优秀的个体；另一方面，适应度值一定时，聚合适应度的大小与抗体浓度值呈负相关，体现出免疫系统的自我调节能力，保证了算法的全局搜索能力。

3.3 免疫遗传算法反演

(1)基因编码：对于纱线原料性能参数反演问题，实数编码无法将离散编码序列和连续微粒位置对应起来，所以本文此处采用8位二进制编码的方式来对微粒进行编码。

(2)种群初始化：当反演的参数为两个时，在一定范围内随机产生1行16列的0、1数值矩阵来初始化种群。

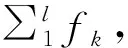
(4)交叉变异：交叉及变异都是形成新个体的一种有效方法，其优点是能够避免部分信息丢失，最大限度的保证了遗传算法的有效性。反演算法部分交叉与变异操作采用正演算法部分的相同操作，不同点在于染色体的编码方式。

(5)基于浓度的群体更新：反演部分群体更新的操作也同正演模型部分的相同，只是此处无需将实数编码转换成二进制编码。

4 仿真实验

先对免疫遗传算法优化的BP神经网络在纱线质量预测上的可行性与效果进行探究，利用来自山东某棉纺厂的29.2 tex精梳纯棉纱配棉及棉纱(均是在相同的生产条件下纺成)质量数据。

经过10次训练仿真后取试验数据的平均值，最后所得结果如表1所示。

表1训练结果

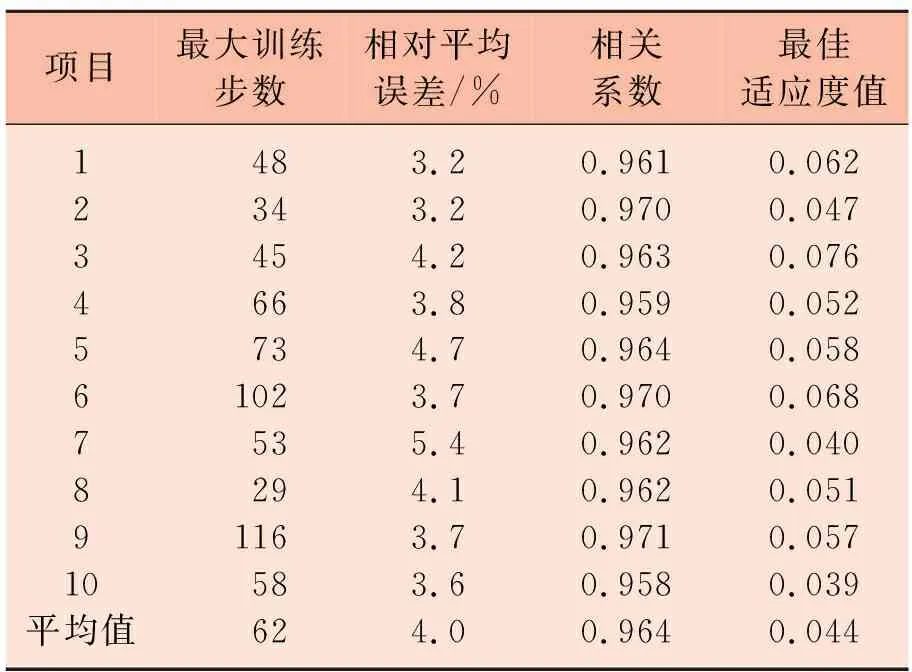
项目最大训练步数相对平均误差/%相关系数最佳适应度值12345678910平均值4834456673102532911658623.23.24.23.84.73.75.44.13.73.64.00.9610.9700.9630.9590.9640.9700.9620.9620.9710.9580.9640.0620.0470.0760.0520.0580.0680.0400.0510.0570.0390.044

在2.1设立的BP神经网络模型的基础上利用Matlab软件进行训练和仿真，BP神经网络的参数设定如下：训练步数为1 000，训练目标为0.000 1，两次显示之间的训练步数为50；另外，网络的激活函数选择tansig函数，训练函数选择trainlm函数。建立免疫遗传BP神经网络模型，对纱线强力值进行预测分析，免疫遗传算法的参数设定为：种群规模为30，进化代数为50，十进制编码方式，适应度比率选择方法，交叉概率为0.8，变异概率为0.2；新增抗体数Z为10，聚合适应度计算公式中常数β设定为-0.6。

如表2所示，其中前30组用于模型训练，后10组数据用于测试神经网络。

表2配棉及棉纱质量数据

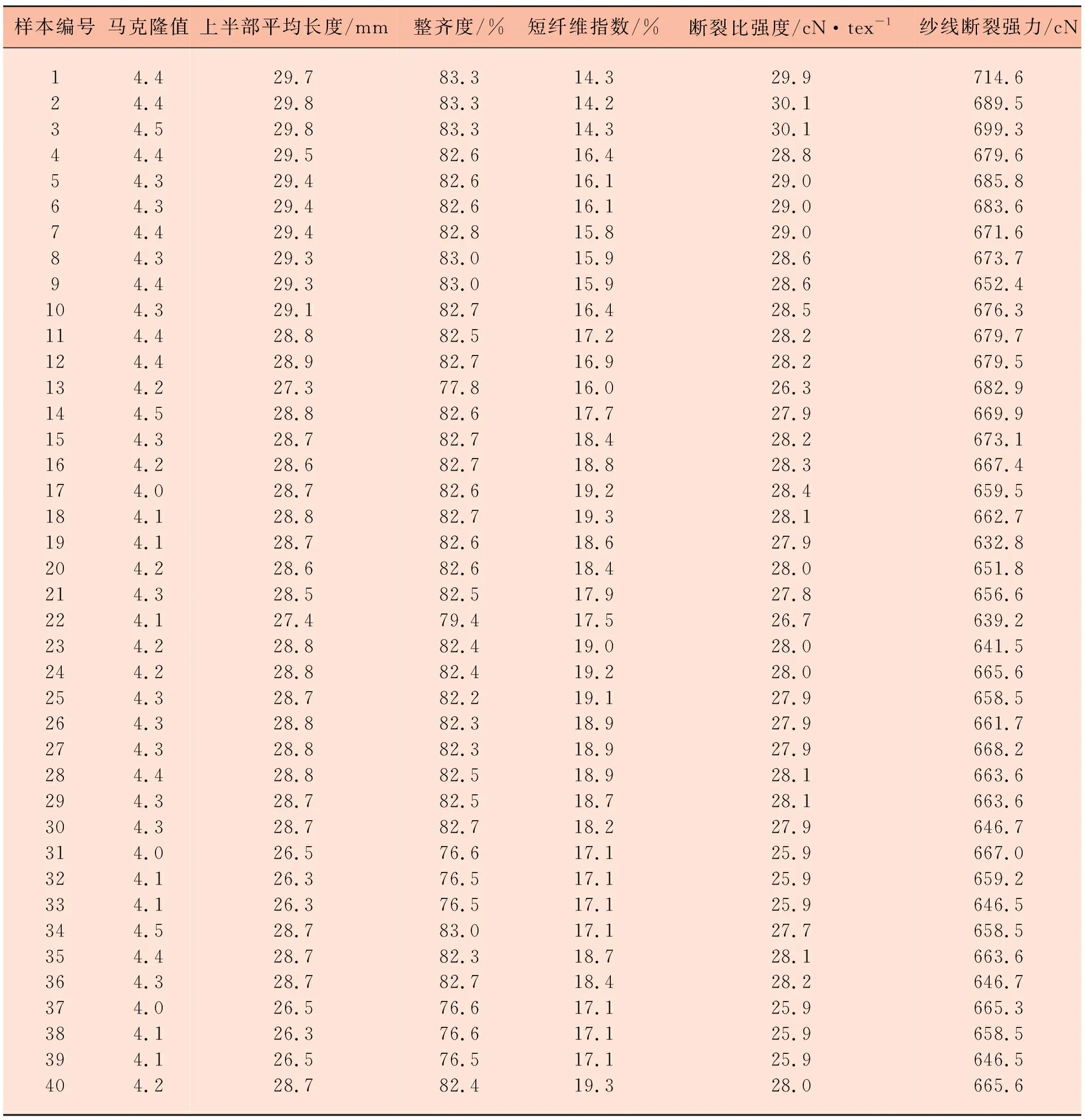
样本编号马克隆值上半部平均长度/mm整齐度/%短纤维指数/%断裂比强度/cN·tex-1纱线断裂强力/cN123456789101112131415161718192021222324252627282930313233343536373839404.44.44.54.44.34.34.44.34.44.34.44.44.24.54.34.24.04.14.14.24.34.14.24.24.34.34.34.44.34.34.04.14.14.54.44.34.04.14.14.229.729.829.829.529.429.429.429.329.329.128.828.927.328.828.728.628.728.828.728.628.527.428.828.828.728.828.828.828.728.726.526.326.328.728.728.726.526.326.528.783.383.383.382.682.682.682.883.083.082.782.582.777.882.682.782.782.682.782.682.682.579.482.482.482.282.382.382.582.582.776.676.576.583.082.382.776.676.676.582.414.314.214.316.416.116.115.815.915.916.417.216.916.017.718.418.819.219.318.618.417.917.519.019.219.118.918.918.918.718.217.117.117.117.118.718.417.117.117.119.329.930.130.128.829.029.029.028.628.628.528.228.226.327.928.228.328.428.127.928.027.826.728.028.027.927.927.928.128.127.925.925.925.927.728.128.225.925.925.928.0714.6689.5699.3679.6685.8683.6671.6673.7652.4676.3679.7679.5682.9669.9673.1667.4659.5662.7632.8651.8656.6639.2641.5665.6658.5661.7668.2663.6663.6646.7667.0659.2646.5658.5663.6646.7665.3658.5646.5665.6

神经网络预测模型训练好以后，通过建立的免疫遗传算法反演模型反演单纤维断裂比强度及短纤维指数两个参数。免疫遗传算法反演模型主要参数设定为:种群数目M=30，进化代数G=50。每个种群的交叉概率及变异概率在一定的范围内随机产生。免疫遗传神经网络算法反演迭代结果如图3所示。由图3可知，该算法迭代不到10次就已经收敛，最佳适应度函数值维持在0.05左右。反演的结果如图4和图5所示。

图3 反演模型适应度函数值迭代曲线

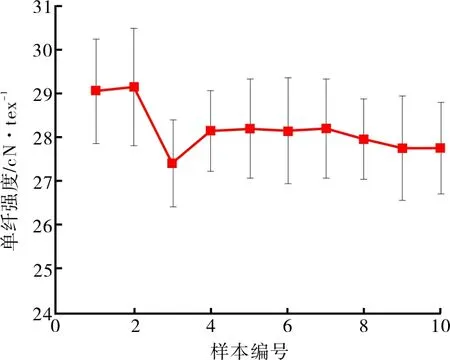
图4 单纤维断裂比强度反演模型预测结果

图5 短纤维指数反演模型预测结果

由图4和图5可知，两个参数的反演精度都很高，预测值十分接近目标输出，误差维持在5%左右。

5 结语

针对传统参数反演算法存在收敛性与稳定性不理想、反演精度较低、计算缓慢以及标准遗传算法存在的早熟收敛等缺点等问题，本文利用免疫遗传算法优化BP神经网络的权值和阈值来建立遗传神经网络正演模型，再根据纱线断裂强力值来反演原棉性能参数，最后以实际纺织生产过程参数进行模型测试，实例验证了算法的可行性和有效性，反演精度达到95%以上。根据本文的反演结果可调节其动态加工生产过程中的敏感参数，使产品质量达标且工艺组合得到优化，同时对企业新产品工艺开发设计的快速决策也具有很好的借鉴作用。