一种预填补社团聚类的兴趣点推荐算法

胡恒德，袁景凌，陈旻骋，王啸岩

(武汉理工大学 计算机科学与技术学院，武汉 430070)

1 引 言

近年来，Web2.0技术得到了迅速的发展，社交网络也随之繁荣，在这种情况下，LBSN[1]也随之蓬勃发展起来，LBSN的流行使得越来越多的用户参与进来，在这些LBSN应用中，用户可以在兴趣点进行签到，同时还可以对兴趣点进行评分以及撰写评论文本.但随着LBSN中用户数量和兴趣点数量的不断增加，LBSN也产生了严重的信息过载问题.规模巨大的用户、兴趣点和信息数量给用户提供了更加丰富的选择，但也导致用户不太容易发现自己感兴趣的兴趣点，因此为应用添加兴趣点推荐算法是十分有必要的.

数据稀疏性是影响推荐系统性能的主要因素之一.Bao等人[2]经过调查发现，目前大多数基于位置的社交网络兴趣点推荐系统中的签到信息过少，而且很多用户都是僵尸用户，这些情况的发生都会导致数据稀疏性问题的进一步加重，此种情况下基于用户或者基于兴趣点的协同过滤算法求得的相似性矩阵会使得推荐精度产生较大的误差.常用的数据预处理方法是矩阵填充技术，包含设定缺省值的方法和降维的方法.设定缺省值的方法，这种方法思想较为简单，方法也有很多种，比如将缺省值直接用评分上下限的中值填充，或者用目标用户(兴趣点)的平均评分填充，还可以使用目标用户(兴趣点)已有评分数据的众数进行填充.这些方法能改善数据的稀疏性，但对推荐质量的提升不大，并且可信度也不够高.降维的方法中，最流行的是奇异值分解技术(SVD)[3]，但SVD存在模型过拟合问题，其次，SVD一般在数据矩阵较为稀疏的情况下表现并不出色.

兴趣点推荐系统中包含有丰富的多源异构数据，如好友关系数据、地理位置数据以及用户对兴趣点的评分等，使用这些数据可以有效提升兴趣点推荐算法的准确率.如Mao等人[4]在计算用户间的相似度时，同时考虑了用户的评分因素以及用户间的地理距离因素.Jamali等人[5]提出了SocialMF模型，并且将信任传播机制融入其中，认为用户与好友、粉丝之间具有信任关系，进而通过矩阵分解的方式来恢复用户好友的矩阵.他们把社交网络关系融入进模型来提高推荐系统的质量.Ahmed等人[6]通过对用户的评论文本信息进行数据提取来建立具有多层异构特征的地理模型.Ference等人[7]改进了基于用户的协同过滤算法，融入了用户位置信息和社交网络信息，为移动端用户提供推荐服务.地理位置作为用户个体信息的一部分，其包含了丰富的隐含信息，通过挖掘用户的行为能够更全面地发现用户的偏好.

为此，本文提出一种预填补社团聚类的兴趣点推荐算法.通过社团聚类算法来分别对好友关系数据以及签到评分数据建模得到用户对兴趣点的个人兴趣和社交兴趣,并添加距离影响因素.从而建立了SoGS模型来进行兴趣点推荐.并且提出一种基于相容类的预填补算法来缓解原始用户-兴趣点评分矩阵的稀疏性问题.

2 基于相容类的预填补算法

2.1 粗糙集信息系统和不可分辨关系

粗糙集[8]理论中知识表达方式一般被称为信息系统，其可以被定义为一个四元有序组S=(U,A,V,f)，其中U是全体对象，即论域；A是所有属性的集合；V=∪a∈ARa，Va是属性的值域；f:U×A→V是一信息函数，作用是为每个对象的所有属性赋予信息值，即∀a∈A,x∈U,f(x,a)∈Va.

若信息系统S的属性值域Va中存在一个属性a的值为*(*即缺失值)，则该信息系统就被称为不完备信息系统，反之则称为是完备的.

2.2 基于相容类的预填补算法

不完备信息系统S=(U,A,V,f)，属于集合P⊆A，相容关系[9]如下：

SIM(P)={(x,y)∈U×U|∀a∈P,f(x,a)
=f(y,a)∨f(x,a)=*∨f(y,a)=*}

(1)

由式(1)可知，相容关系是自反以及对称的，但不一定是传递的，仍然属于广义的不可分辨关系.

SP(x)表示对象集合{y∈U|(x,y)∈SIM(P)}，则SP(x)代表与对象x不可分辨的对象的最大集合，即SP(x)成为x在P上的相容类.

MOS是信息系统 的不完备对象集合[29]：

MOS={x∈U|∃a∈R,f(x,a)=*}

(2)

依据相容类内部的不可分辨关系，本节给出一种基于相容类的预填补算法，该算法引入了粗糙集的相关知识，通过对缺失对象计算其相容类，根据相容类内部广义上的不可分辨对象来为缺失值进行填补，缓解了评分矩阵的稀疏性.

基于相容类的预填补算法步骤如下：

Step1.计算原始用户-兴趣点评分矩阵S的不完备对象集合MOS，xi表示第i(i=1,…,|MOS|)个用户对象.

Step2. 遍历不完备对象集合MOS中的每个用户对象xi，计算xi的相容类SR(x).若SR(x)为空，则不对此对象进行填充；若|SR(x)|=1，则根据此对象的属性值对缺失数据进行填充；若|SR(x)|>1，则根据xi缺失属性在形容类内对应的众数进行填充.

Step3. 返回填补之后的用户-兴趣点评分矩阵S.

该算法伪码表示如下：

输入：原始用户-兴趣点评分矩阵

输出：预填补后的评分矩阵

1.FOR EACH data recorddINSDO //遍历用户-兴趣点评分矩阵

2. FOR EACH attributeaINdDO

3. IFa="*" THEN

4.MOS.add(d)；//将第此条用户对象加入到MOS中

5. END IF

6. END FOR

7.END FOR

8.FOR EACH data recorddINMOSDO //遍历MOS

9.SR(d)←Compatible(d)；//计算用户对象d的相容类

10. IF |SR(d)|=0 THEN

11. Nofill(d); //若d的相容类为空，则不做填补

12. ELSE IF |SR(x)| THEN

13. FillwithoneRecord(d); //根据此条用户数据填补缺失评分

14. ELSE

15. FillwithCompatible(d); //根据相容类中对应众数评分填补

16. END IF

17.END FOR

18.RETURN

3 社团聚类与多源数据融合的SoGS模型

本文通过计算用户对兴趣点的签到概率，并选择概率最大的TopN兴趣点作为推荐列表返回给用户，从而达到了兴趣点推荐系统的目标.在本文提出的SoGS模型中，认为决定用户访问兴趣点的因素有两方面，一个是距离，另一个是兴趣.在距离方面，可通过对地理位置数据建模来度量.在兴趣方面，又可分为个人兴趣和社交兴趣，从用户的历史评分数据中可以分析出该用户的兴趣偏好，因此本文中个人兴趣可由用户-兴趣点评分矩阵挖掘得到；而用户对兴趣点的喜好容易受好友的影响，并且有相同爱好的人容易建立好友关系，因此本文中社交兴趣可由社交网络数据建模得到.

3.1 基于用户偏好聚类的社团发现算法

基于用户兴趣偏好聚类的社团发现算法是根据凝聚算法的思想，将具有相同偏好的用户凝聚到一起，组成社团.根据用户-兴趣点评分矩阵定义用户兴趣偏好矩阵为A，其中A的行与列是m×n，aij代表用户对兴趣点的评分，即用户i对兴趣点j的兴趣偏好.定义社交网络中的社团集合为空集：C≠Ø，用户集合包含所有用户：U={u1,u2,…,un}，并且用户的兴趣偏好为p={ai1,ai2,ai3,…,ain}.

传统的协同过滤算法在进行用户间相似性计算时，主要有皮尔逊相关系数、约束皮尔逊相关系数和余弦相似度等计算方法.皮尔逊相关系数和约束皮尔逊相关系数都会利用用户对兴趣点的评分，不适合01签到矩阵.用户间相似度计算的是两个兴趣偏好向量的相似程度，因此本文使用公式(3)余弦相似度来度量.

(3)

其中U和V表示用户空间U中任意两位不同用户，wu,v表示U，V之间的相似性；Iuv表示u和v的共同评分集合，Ru,i和Rv,i表示用户u和v分别对项目i的评分.

因为要判断用户能否加入某一社团，因此定义社团凝聚度cs(community cohesion)公式如下：

(4)

其中，ci∈C，m表示社团ci中的用户数量，cos(ui,v)表示用户ui与v的余弦相似度，社团凝聚度cs(ui,cx)是目标用户ui与社团cx中每个用户相似度的累加之后再求平均得到的.设置判断用户能否加入某一社团的阈值为μ，若cs(ui,cx)>μ，则表示目标用户满足加入该社团的条件.

基于用户兴趣偏好聚类的社团发现算法步骤如下：

Step1.从U中抽取一个用户作为u1，然后创建新社团c1，使得u1∈c1，此时U={u2,u3,…,un}，C1={u1},C={c1}.

Step2. 从U中抽取用户ui，遍历C={c1,c2,…,cm}中的每一个社团cx，计算ui与cx的社团凝聚度cs(ui,cx)，然后把cs(ui,cx)与阈值μ进行比较，大于阈值μ则ui∈cx.若遍历结束后用户ui并没有能够加入任何一个社团cx，则组成新的社团cm+1，ui∈cm+1，C={c1,c2,…,cm,cm+1}，并从用户集合U中删除该用户ui.

Step3. 若U为空集，则此时算法结束，否则，返回到步骤2继续执行.

该算法伪码表示如下：

输入：社交网络社团集合C≠Ø，用户集合U={u1,u2,u3,…,un}，阈值μ

输出：社交网络社团集合C={c1,c2,…,cn}

1.FOR EACH user recorduiINUDO //遍历用户集合

2. IF check (ui) //若ui是用户集合U中的第一个用户

红一、四方面军川西北会师后，针对西北地区民族构成特点，中共中央专门制定《关于少数民族中党的基本方针》，提出“争取少数民族在中国共产党领导下对于中国革命胜利前途有决定的意义。”红军进入甘南藏区，面临粮食奇缺的巨大困难，红军坚持执行严格的军纪，不仅逐渐取得沿途藏族群众的理解，而且还得到当地少数民族的支持援助。卓尼土司杨积庆为红军北上让出通道，“将曹日仓的麦粮暗中开放接济了过境的红军。当时这个仓设两个仓库，共装小麦四、五十万斤。红军走后，一个仓库内的粮食全部吃用完，另一个仓库里用去了多半仓。”[5]P141就是中国共产党领导红军执行民族政策的典型事例。

3.ui∈c1,C.add(c1)

4. END IF

5. FOR EACH communitycxINCDO //遍历社团集合

6. IF (cs(ui,cx)>μ) //若用户ui与社团cx的社团凝聚度cs大于阈值

7.ui∈cx，flag=true //将用户ui加入到社团cx中，并标记

8. END IF

9. END FOR

10. IF (flag==false) //若用户没有加入任何社团

11.ui∈cm+1,C.add(cm+1)//新建社团cm+1

12. END IF

13. END FOR

3.2 基于社团聚类的兴趣偏好建模算法

在上节中提出的基于用户偏好聚类的社团发现算法的作用是利用用户的兴趣偏好信息，即兴趣点推荐系统中的用户-兴趣点评分矩阵进行聚类，从而得到所需的兴趣偏好社团集合.但实际上该算法同样可适用于用户-用户好友关系矩阵，此时兴趣偏好被解释为社交好友关系.若用户之间存在好友关系，则用户-用户好友关系矩阵中相应的位置值是1，反之则是0.

本节给出一种基于社团聚类的兴趣偏好建模算法，此算法融合了社团结构、用户的兴趣偏好信息以及用户间的社交好友关系对兴趣点推荐的影响，并且还通过社团聚类方法来达到提前建立模型以及缩小近邻搜索空间的目的.

基于社团聚类的兴趣偏好建模算法步骤如下：

Step1. 初始化，定义社交网络G，用户集合为U={u2,u3,…,un}，CF表示好友关系社团集合，CP表示兴趣偏好社团集合.

Step2. 建立模型，在G上执行基于用户兴趣偏好聚类的社团发现算法，分别得到好友关系社团集合CF和兴趣偏好社团集合 .

Step3. 从CF和CP中分别取出含用户i的好友关系和兴趣社团集合CF(i)与CP(i)，并按照公式(5)和(6)分别取并集.

CF(i)=CF(i)1∪CF(i)2∪…∪CF(i)n

(5)

CP(i)=CP(i)1∪CP(i)2∪…∪CP(i)n

(6)

(7)

Step5. 用公式(8)计算用户i对兴趣点l的预测评分Si,l：

(8)

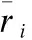
wi,j=cos(i,j)*σi,j

(9)

其中cos(i,j)表示用户i和j间的余弦相似度，可根据公式(3)计算，参数σi,j的计算方法是同时包含用户i和j的社团数量除以总的社团数量，这里考虑了社团重叠度的影响.

Step6. 选取预测评分最高的TopN兴趣点作为推荐列表返回给目标用户i.

3.3 SoGS模型建模过程

一个用户的签到行为不光受用户的兴趣偏好影响，同样也受到他与兴趣点间的地理距离的影响.Ye等人[10]针对Foursquare和Gowalla[11]数据集进行了空间分析，研究发现用户通常在距离自己住所较近的兴趣点签到，并且两个连续签到兴趣点之间的距离一般较近.本文在同时考虑社团聚类、地理位置信息数据、用户-兴趣点评分数据和用户好友关系数据的基础上，提出了一种新的兴趣点推荐模型SoGS.通过朴素贝叶斯分类器来对地理位置数据进行建模得到用户与兴趣点间的距离，其主要是基于目标用户整体的签到评分情况来对未签到的兴趣点进行概率计算.对某一用户来说，把其已签到的兴趣点作为一个类簇，那么再向该用户推荐新的兴趣点就可以转化为新兴趣点的分类问题，此时要分配的类别只有一个，同时要推荐的新兴趣点数量众多，因此可以使用朴素贝叶斯算法计算新的兴趣点属于目标类别的概率大小，然后选择概率值最大的TopN个兴趣点推荐给用户.

设Li是用户ui已经签到的兴趣点集合，且为一个分类集合.Pr[Li]是用户在兴趣点集合中所有兴趣点都签到的概率.可认为此概率与兴趣点间的距离有关，因此Pr[Li]的计算公式可定义如下：

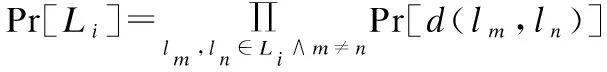
(10)

其中d(lm,ln)代表兴趣点lm和兴趣点ln间的距离.Yelp以及Foursquare数据集的签到数据都包括了兴趣点的经纬度信息.刘树栋等人[12]说明了计算两个GPS经纬度坐标之间的距离应使用大圆距离公式[13].定义兴趣点lm的坐标为(latm,lonm)，兴趣点ln的坐标为(latn,lonn)，则可根据大圆距离公式计算d(lm,ln).

d(lm,ln)=R·arccos[coslatm·coslatn·cos(lonm,lonn)+
sinlatm·sinlatn]

(11)

其中，R为地球半径.当d(lm,ln)越小时，用户签到的概率越大，即Pr[d(lm,ln)] 越大，因此根据此反比关系，可得如下公式：

(12)

对于一个兴趣点lj(lj∈L-Li)，用户在兴趣点lj签到的概率可以简化为：

(13)

在一般情况下，用户的待推荐兴趣点数量众多，因此要防止Pr[lj∪Li]向下溢出，故对上式结果取对数，得到公式(14)：

(14)

可以对其进行标准化，设计一个标准化公式，设计出了用户ui对兴趣点lj签到概率公式如下：

(15)

pD(ui,lj)即是用户与兴趣点间距离的度量.

使用公式(8)可以计算出目标兴趣点的预测评分，再对其进行归一化处理即可得到用户ui对兴趣点l签到概率，即用户对兴趣点的兴趣的度量.公式如下：

(16)

pl(ui.l)即是用户与兴趣点间兴趣的度量，是个人兴趣与社交兴趣的综合权衡结果.

故定义用户对兴趣点的最终访问概率公式如下：

p(i,l)=(1-γ)pD(i,l)+γpI(i,l)

(17)

式(17)中γ是用来调节用户与兴趣点之间的距离以及兴趣在概率计算中的比重大小.当γ等于1时，只有兴趣起作用，这时不需要对地理位置数据进行建模.当γ等于0时，只有距离起作用，这时不需要对个人兴趣以及社交兴趣进行建模.由此可见，当目标用户在LBSN系统中存在部分数据缺失时，模型仍可以在一定程度上维持推荐的稳定性，即具有良好的鲁棒性.

4 实 验

4.1 实验数据集

本节实验使用的是Yelp数据集.Yelp是美国最大的点评类网站，在该网站与其移动端应用中，用户可以在兴趣点签到，为兴趣点评分并撰写评论文本，还可以添加好友.

Yelp数据集统计信息如表1所示.

4.2 评价标准

表1 Yelp数据集统计信息Table 1 Statistics of Yelp dataset

为验证推荐模型的性能，本节使用准确率Precision和召回率Recall[14]来验证.准确率是指正确为用户推荐的兴趣点数量占推荐兴趣点总数的比率，衡量的是推荐算法的精确度，召回率是指正确为用户推荐的兴趣点数量占用户访问过的兴趣点总数的比率，衡量的是推荐算法的查全率.

准确率(Precision)和召回率(Recall)公式如下：

(18)

(19)

其中Svisited代表测试数据集中用户签到过的兴趣点集合，SK,rec代表前K个被推荐的兴趣点集合.最后准确率和召回率的值是测试集中所有用户的平均值.

4.3 实验结果与分析

为了验证SoGS模型的性能，本文选取了三个经典的模型进行对比：

1)PMF：概率矩阵分解模型[15]，其假设用户和兴趣点的隐式特征向量服从高斯先验分布，主要作用于用户-兴趣点评分矩阵，通过分解与学习预测缺失值.

2)NMF：非负矩阵分解模型[16]，该模型在PMF模型的基础上对分解完成的矩阵加上非负的限制条件，比较符合特定场景的要求.

3)CoRe：该模型基于鲁棒性规则融合了用户社交关系和地理因素，其中地理因素是基于核密度估计进行建模[10].

4.3.1 标准情况下SoGS模型实验

在SoGS模型中，使用基于社团聚类的兴趣偏好建模算法对个人兴趣以及社交兴趣进行建模时，阈值μ选择实验得到的最优值0.4.实验中按照8:2的比例随机将原始数据集分成为训练数据集和测试数据集，在调节距离和兴趣的影响比例时，使用简单交叉验证设置γ为0.35.

图1 4个模型在Precision指标上的对比Fig.1 Comparison of four models on Precision

由图1和图2，PMF和NMF模型在指标上的表现不好，这是因为它们仅采用了评分作为模型的输入，因而并不能很好地描述用户的偏好，并且对于解决数据稀疏性以及冷启动问题有天然的弱点.CoRe模型整合了用户社交关系和兴趣点地理因素，并没有考虑相关类别信息和评分信息，但其采用一个具有鲁棒性的规则而不是简单的线性加权来对用户的社交关系和地理因素进行融合，同时对地理因素也进行基于核密度估计的建模，因此它体现出第二优秀的推荐精度.由于SoGS模型同样使用一个具有鲁棒性的规则融合了地理位置因素、社交好友关系以及评分数据，能够更加细致地描述用户偏好，因此与其他3个对比算法相比，SoGS模型在准确率和召回率上有更优的表现.随着推荐兴趣点个数k的增加，造成4个模型准确率不断下降以及召回率不断上升，这是由Precision和Recall的计算公式决定的.

图2 4个模型在Recall指标上的对比Fig.2 Comparison of four models on Recall

4.3.2 基于相容类的预填补算法结合SoGS模型实验

本文的第2部分提出了一种基于相容类的预填补算法，通过对原始数据集进行预填充来缓解数据稀疏性问题，提升了一定的推荐精度，但仍需要通过实验验证其与SoGS模型结合后的推荐质量.

CC-SoGS(Compatible Class-SoGS)：首先对用户-兴趣点评分矩阵使用基于相容类的预填补算法进行预处理，然后再通过SoGS模型为用户进行推荐.

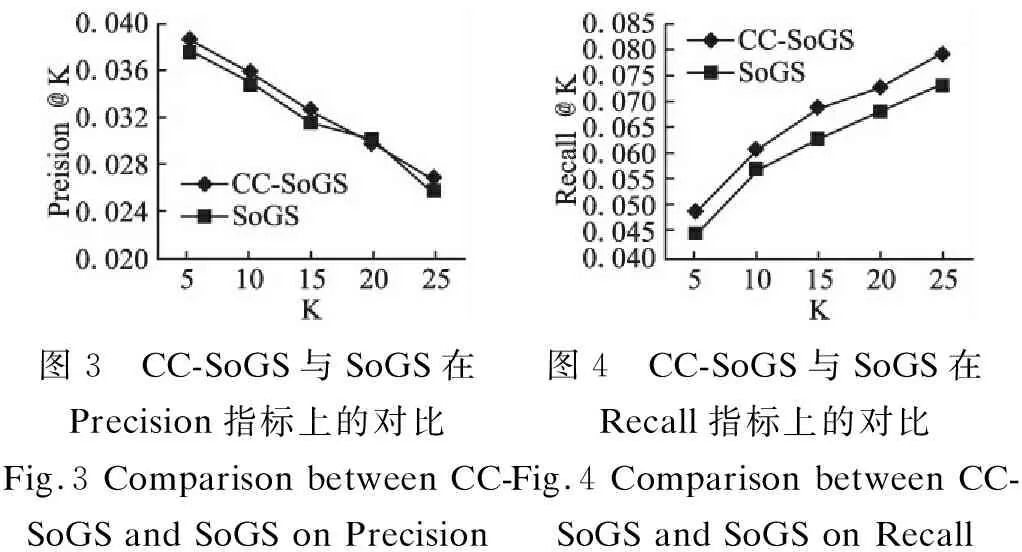
图3 CC-SoGS与SoGS在Precision指标上的对比Fig.3 Comparison between CC-SoGS and SoGS on Precision图4 CC-SoGS与SoGS在Recall指标上的对比Fig.4 Comparison between CC-SoGS and SoGS on Recall

由图3和图4可以看出，近邻个数k的不同取值情况下，CC-SoGS模型比SoGS模型在Precision和Recall指标上的表现基本都更加优秀，这是因为CC-SoGS使用了基于相容类的预填补算法有效缓解了用户-兴趣点评分矩阵的稀疏性问题.

5 结 论

针对兴趣点推荐算法所面对的数据稀疏性问题，本文提出了一种基于相容类的预填补算法，缓解了用户-兴趣点评分矩阵的稀疏性问题.通过社团聚类算法分别对签到评分数据以及好友关系数据建模得到用户对兴趣点的个人兴趣和社交兴趣,并添加距离影响因素.从而建立了SoGS模型来进行兴趣点推荐.SoGS模型中用户对兴趣点的访问概率由用户与兴趣点间的距离、用户对兴趣点的个人兴趣和社交兴趣这三个因素决定.结果分析证明，SoGS模型能够提高准确率和召回率，并且在部分信息缺失的情况下仍具有良好的推荐性能，表现出了一定的鲁棒性，获得了更好的推荐效果.