八种化归策略助你轻松解题
李苏娟
(江苏省兴化市戴泽初级中学 225721)
“化归”是转化和归结的简称,所谓化归思想,就是把所要解决的问题转化归结为另一个较易解决的问题或已经解决的问题,具体地说,就是把“新知识”转化为“旧知识”,把“未知”转化为“已知”,把“复杂”转化为“简单”,把“陌生”转化为“熟悉”.一言以蔽之,解题过程的实质就是转化过程.化归思想注重寻求问题与已有知识经验的逻辑关联,从而化生为熟、化繁为简、化隐为显、化难为易,使问题得以顺利解决.下面举例说明常用的八种化归策略,希望能助你轻松解题.
一、多元向一元化归
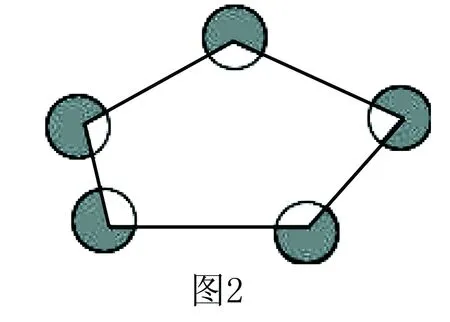
例1 (2006年全国初中数学竞赛试题)已知a,b,c为整数,且a+b=2006,c-a=2005.若a 分析要求a+b+c的最大值,由于a,b,c都是不确定的整数,所以这里有三个变元.为了减少变元的个数,我们可利用已知条件a+b=2006,c-a=2005,采用消元法来达到目的. 解将a+b=2006,c=a+2005两边相加得a+b+c=a+4011.因为a 点评这里待确定最大值的代数式中有三个变元,确定每一个变元的最大值都有一定的难度.我们利用整体思想,从整体上思考a+b+c的最大值,再借助于消元法得到只有一个变元的代数式a+4011,从已知条件中找出a的最大值,则问题就迎刃而解了.解决多元问题的基本思想是消元,将其转化为一元,消元的基本方法是代入法和加减法. 分析注意到求值式中含有m2,而已知条件m2-3m+1=0可以变形为m2=3m-1,利用它即可运用逐步降次的方法来求出代数式的值. 点评本题若将求值式直接通分,则会出现4次方,求值困难.一般地,对于高次问题,常采用上述方法来逐步降次,达到解决问题的目的.下面的问题你不妨运用这个方法试一试: (2017年四川省内江市中考题)若实数x满足x2-2x-1=0,则2x3-7x2+4x-2017=____.(答案:-2020) A.-1或3 B.-1 C.3 D.1或-3 分析把分式方程转化成整式方程,求出整式方程的解,再代入最简公分母x(x+1)进行检验,排除增根即可. 解方程两边同时乘以x(x+1),得3=x(x-2),整理得x2-2x-3=0,解得x1=-1,x2=3.当x=-1时,x(x+1)=0,舍去;当x=3时,x(x+1)=12≠0,所以x=3是原分式方程的解,选C. 点评解分式方程的基本思想是转化,即将分式方程转化为整式方程来求解.但必须注意:(1)去分母时各项都要乘最简公分母,不能漏乘;(2)去括号时要注意括号前的符号;(3)移项要变号;(4)一定要检验. 例4 (2017年浙江省衢州市中考题)如图1,正△ABO的边长为2,O为坐标原点,A在x轴上,B在第二象限,△ABO沿x轴正方形作无滑动的翻滚,经一次翻滚后得△A1B1O,则翻滚3次后点B的对应点的坐标是,翻滚2017次后AB中点M经过的路径长为. 分析先求出点B和点B3的坐标,再探究出其中的规律后,利用规律将无限向有限转化,进而解决问题. 点评本题考查点的运动轨迹的确定及其长度的计算、规律的探索、扇形的弧长公式、等边三角形的性质等知识,解题的关键是从特殊到一般探究出规律,再利用规律将无限向有限化归,进而顺利地解决问题. 例5 (2017年辽宁省朝阳市中考题)如图2,分别以五边形ABCDE的顶点为圆心,以1为半径作五个圆,则图中阴影部分的面积之和为( ). 解∵五边形的内角和为(5-2)×180°=540°,∴5个圆形的空白部分的面积之和 点评有些问题,从表面上看要局部求出有关量,但若从整体上去把握这些量之间的关系,则思路更明朗,方法更巧妙. 例6 (2017年四川省宜宾市中考题)规定:[x]表示不大于x的最大整数,(x)表示不小于x的最小整数,[x)表示最接近x的整数(x≠n+0.5,n为整数),例如:[2.3]=2,(2.3)=3,[2.3)=2.则下列说法正确的是.(写出所有正确说法的序号) ①当x=1.7时,[x]+(x)+[x)=6; ②当x=-2.1时,[x]+(x)+[x)=-7; ③方程4[x]+3(x)+[x)=11的解为1 ④当-1 分析根据规定的[x]、(x)、[x)的意义,将陌生的数的计算、方程与不等式的解法和函数图象的交点坐标问题转化为常规的问题来处理,再结合给出的说法进行判断,得到答案. 点评对于新定义运算问题,关键是要认真读题,正确领会所给运算规则,将其转化为常规运算来处理.由于[x)表示最接近x的整数,为了排除x=n+0.5(n为整数)的情况,题目附加了条件x≠n+0.5(n为整数),因此需要将-1 图4也是一种无限分割:在△ABC中,∠C=90°,∠B=30°,过点C作CC1⊥AB于点C1,再过点C1作C1C2⊥BC于点C2,又过点C2作C2C3⊥AB于点C3,如此无限继续下去,则可将△ABC分成△ACC1、△CC1C2、△C1C2C3、△C2C3C4、…、△Cn-2Cn-1Cn、….假设AC=2,这些三角形的面积和可以得到一个等式是. 点评这里通过对图形的无限分割,借助于图形面积的计算,利用总体等于部分之和,得到了一个数量等式,是数形之间化归的典范. 例8 (2017年浙江省绍兴市中考题)如图5为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1500 m,小敏行走的路线为B→A→G→E,小聪行走的路线为B→A→D→E→F.若小敏行走的路程为3100 m,则小聪行走的路程为m. 分析本题的难点是如何用小敏行走的路程来求小聪行走的路程,即小聪行走的路程与小敏行走的路程存在怎样的关系.比较两人走的路线,发现小敏走的路程为AB+AG+GE=1500+(AG+GE)=3100,则AG+GE=1600 m,小聪走的路程为BA+AD+DE+EF=3000+(DE+EF).下面关键是寻找AG+GE与DE+EF的关系,这样就把实际问题转化为数学问题.观察图形可知,正方形的对角线平分一组对角,GE⊥DC,易得DE=GE,于是只要说明AG=EF即可,而EF是矩形CEGF的对角线,易知EF=CG.于是,连接CG,由正方形的对称性易知AG=CG,从而问题获解. 点评本题初看上去比较复杂,但经过分解化归,问题得到了简化,即寻找AG+GE与DE+EF的关系,再结合几何图形的特点,便将问题化归为说明正方形中两条线段相等的问题,然后运用正方形、矩形的有关知识,很快找到了解决问题的途径.至此我们发现,本题主要考查正方形的性质、全等三角形的性质和判定、矩形的性质及等腰三角形的性质.解决问题的关键是证明AG=EF,DE=GE.二、高次向低次化归


三、分式向整式化归

四、无限向有限化归


五、部分向整体化归



六、陌生向熟悉化归

七、数形之间化归




八、实际问题向数学问题化归


