基于STATCOM的DFIG风电机组低电压穿越策略研究

吴彦廷

（浙江省杭州学军中学紫金港校区，浙江杭州，310000）

0 引言

我国在风电装机容量方面取得重大突破，随着八大千万千瓦级风电基地的规划和建成，中国已成为风电装机容量最大的国家。预计到 2020 年，我国风电装机容量将达到2. 0 亿 kW[1]。但由于LVRT（低电压穿越）能力方面的欠缺，大规模风电接入所连接电网的安全运行仍存在重大隐患。

2011 年以来，河北、甘肃、吉林等风电基地相继发生的多起大规模风电机群脱网事故足以佐证。为此，国家标准化管理委员会颁布了《风电场接入电力系统技术规定》求并网风电机组具备LVRT 能力[2]。并且要求风电场在正常运行条件下能够调节公共接入点（即PCC点）的电压以及无功功率，最大限度地缩小不稳定的风速对电压的扰动影响，保证PCC点处电压波动相对稳定。

为解决风电系统不断增加的穿透功率，变化幅度较大的风速和多变的系统运行方式等造成扰动引起的电压波动问题。通常在升压站装设动态无功补偿设备，例如静止无功补偿器（SVC）和静止同步补偿器（STATCOM）等[3,4]，用于DFIG双馈风电机组等无功补偿的能力。而STATCOM相对于SVC而言，具有大的工作范围宽、易于稳定控制，且能够快速响应的特点，然而其高昂的设备成本和维修费用，是目前受限于风电机群控制的主要原因。与SVC[5]相比，STATCOM最为明显的优势在于其无功补偿的能力不受到外界电压的影响，因此其具有很强的电压支撑能力。除此以外，程启明[6]采用了风电场多种工况下的电压控制，从而维护风电场在受到外界风速波动情况下导致的电网母线PCC点的电压和电流的稳定，从而为风电机组等有功和无功的有效控制提供一种更为直接的方式。

然而，由于低电压穿越LVRT能力欠缺容易导致安全问题，国内外专家学者在LVRT控制策略和保护原理方面投入大量精力研究[7,8]。其中文献考虑Crowbar阻值和退出时间的双馈风电机组低电压穿越推导了DEIF在并网运行情况下，发生机端三相短路后的最大转子电流估算式。同时,胡家兵[9]分析并研究了 Crowbar电阻阻值，短路电流的最大值及出现最大值时间之间的关系 ,同时也研究了不同Crowbar 电阻阻值以及不同的退出时间对 DFIG 的 LVRT效果的影响。

文献[10] 给出了一种DFIG风力发电系统无功极限值的计算方法，并讨论了在强电网无功调节的方式中DFIG风电场的应用，并且给出了通过DFIG风电场就近对当地用户直接进行无功补偿的方式，同时也给出了与之对应的无功分配策略，文献 [11] 配置 STATCOM 的 DFIG 风电场在不对称电网故障下的控制策略研究在不对称电网故障穿越的第 2 阶段，双馈式(doubly-fed induction generator，DFIG)风电场如何实现“自身不脱网安全运行并同时满足并网导则无功支撑要求”的问题。

同时本文也对分散的DFIG风电机组与 PCC电压接入点之间的物理紧密程度进行了考虑和分析，通过建立DFIG风电场无功电压多目标优化控制模型，并采用基于过滤集合的内点法进行求解，以此完成对不同风电机组之间、集中无功补偿设备之间与风电机组的协调控制。

1 基于无功功率分析的DFIG低电压穿越研究

■1.1 双馈异步发电机无功功率的分析

在双馈电机变速恒频风力发电方案中，转子通过由两个反向连接的PWM变换器构成的“交流—直流—交流”变换器与电网间接相连，定子则是直接接入电网。其中靠近DFIG转子一侧PWM变换器的称为转子侧变换器，靠近电网一侧的则被称为是网侧变换器。工作中，在高功率因数整流模式下，网侧变换器为转子侧变换器提供直流母线电压。同时为了实现DFIG的变速恒频运行，转子侧变换器将会对转子的电流电压进行控制。其中，DFIG变速恒频风力发电系统功率关系如图1所示。

图1 DFIG的变功率变换关系原理图

图中，Pmec表示输入DFIG的机械功率；Ps表示定子发出的有功功率，Qs则表示定子发出的无功功率。Pc表示网侧变换器从电网输入的有功功率，Qc则表示电网输入的无功功率；Pg、表示DFIG风电系统流入电网的有功功率,Qg表示其无功功率。

在理想状况下，定、转子绕组的损耗可以忽略不计，可得到以下关联关系

由于定子侧有功功率的转差功率等于转子侧的有功功率，则可得以下公式

式中Pmec（风力机输入的机械功率）的值受风力机的捕获能力大小，风力机转速控制规律影响。目前，为了使风力机输入的机械功率尽可能大，现今的DFIG风能转化率的提升通过对变速恒频风电机组的转速控制规律来完成

同样的，在理想状况下，我们忽略功率变换器的开关损耗和线路损耗，由能量守恒定律，我们可以得到：

由于转子侧的有功功率方向与转差率的正负相关，可通过转差率的符号来显示DFIG的工作状态，例如，正的转差率表示DFIG的亚同步状态，负的转差率表示其正处于超同步状态，而转差率为零时，DFIG则处于同步运行状态

假设系统损耗为零，那么DFIG输入电网系统的有功功率和无功功率数值相等。即下式：

由DFIG的数值模型可以看出，DFIG转子侧和定子侧的相关关系为：

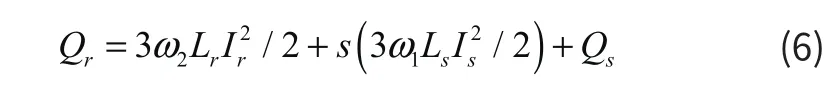
式中：上式中：定子和转子侧电流的最大值分别为：Is、Ir；定子侧、转子侧的漏感及励磁电流分别为Ls 、Lr；定子侧的电流角频率为ω1；转差角频率为ω2。

由此可知，双馈电机转子端输入的无功功率有两个作用，一是提供给转子绕组，二是按一定比例(转差率) 向定子绕组传递一部分无功。

■1.2 DFIG 风电机组电压穿越的控制策略

基于各国提出的风电场并网导则，我们可以将电网依据故障的时间分类，可以分为：初始阶段、持续阶段以及恢复阶段。鉴于我国在第一阶段的研究已比较成熟，第三阶段的解决方法也相对容易。在此我们具体给出第二阶段即故障持续阶段对风电机组的控制策略。

关于在第二阶段，我们首先需要考虑的的是防止风力发电机组脱网的问题。以及并网导则对于正序无功电流的要求。值得一提的是，双馈风力发电机组由于自身变流量的问题，无法保证所有控制目标的精度，因此要考虑控制方法优先级的问题。相较于满足并网导则对于无功支撑的要求，风电机组自身不脱网安全运行的控制优先级较高。在此，我们从转子侧变流器RSC方面考虑，给出RSC正负序电流指令算法。其实我们也可从网侧变流器GSC方面考虑，在此不做过多说明。

对于RSC而言，消除DFIG转矩脉动应设为第1优先级，在此基础上分析，首先给出核心思想：我们在保证消除DFIG电磁转矩脉动的前提下，尽可能在RSC电流上限值以内满足并网导则对于正序无功电流的要求。

接着是对定子和转子侧的分析，定子侧和转子侧的方向设定均以电动机的常用惯例为准，定子坐标系中矢量形式的DFIG 定、转子电压和磁链方程为

上式中：定子侧、转子侧电阻分别为：RS,； 定子侧转子侧的定子自感、互感、转子互感分别为Lm,Ls,L′

r。定子侧、转子侧的空间矢量分别为vsαβ,；定子侧转子侧的电流空间矢量分别为；转子电角速度为ωr；定、转子磁链空间矢量分别为。其中上标 “ ’ ” 表示绕组折算到定子侧后的物理量。

在不对称的电网电压下，DFIG各自电磁量的存在正序和负序，因此电流、电压以及磁链空间的表达式分别为

式中：电压、电流或磁链空间矢量为F ；上标正、负序分量分别为“p ，n”； 正、反转同步旋转坐标系下标分别为“dq + ， dq - ”；同步电角速度为sω。

由于电网电压的不对称性，输出至电网的DFIG 定子的瞬时有功、无功功率可以表示为

式中：

给出不对称电网电压条件下 DFIG 的电磁转子表达示:

上式中np表示极对数。

可见，若要最大限度地减小 DFIG 电磁转矩的脉动带来的扰动影响，需满足 Tesin2= Tecos2= 0的条件。在此，我们使用正、负序定子电压矢量定向的方式，由式 (12) 可知，对于 DFIG 转子正序有功，无功电流与负序有功，无功电流的指令值之间需满足下列关系式

可以通过结合式 (8) 和 (9) 来满足“ SDLWindV ”对于正序无功电流输出的要求， 因此将DFIG 的转子正序无功电流指令值设为

我们需要控制转子正负序电流的指令值在 RSC 的电流上限值以内，以防止 RSC 出现过流的情况，同时考虑到RSC 的电流限制条件为：

结合式 (13) - (15) ， RSC 正负序电流指令值算法如图 2所示。我们便以此为控制DFIG风电机组的控制策略。在满足并网导则对于正序无功电流的要求的前提下，如有剩余的电流裕量，则用于产生式 (16) 中电磁转矩的平均值Te0。

图2 RCS电流指令算法流程图

表1 RCS 电流指令值计算结果

2 总结与展望

LVRT（低电压穿越）能力方面的欠缺给我国风电机领域发展带来巨大困难。由于该原因，国风电机场曾发生多起安全事故。为解决上述原因带来的问题，本文从PCC点入手，通过研究控制PCC点的电压波动来解决低电压穿越造成的问题。在进行双馈异步发电机的无功功率分析后，我们从转子侧变流器RSC方面考虑，采用RSC正负序电流指令算法来控制，使得在保证消除 DFIG 电磁转矩脉动的前提下，尽可能在 RSC 电流上限值以内满足并网导则对于正序无功电流的要求，一次来解决该类问题。

在实际应用方面，本文仍有欠缺，文中只给出此法在风电机组的应用数据，即在单个风电机组中有效。但对于在风电机群的应用效果，由于无实际数据作为理论支撑，并不知道实际效果如何。希望将来的研究能够向风电机群的电压控制方向迈进，使得能源得到充分利用。