原信息与映射信息组合的多核学习降维方法

李 旭，王士同

江南大学 数字媒体学院，江苏 无锡 214122

1 引言

分类算法中，如果样本数据是线性不可分的，那么可以通过一个映射函数将样本数据投影到高维空间中，从而在高维空间中能够找到一个分类超平面[1]。核学习方法就是一种为解决数据线性不可分问题而产生的方法，早在1909年核方法[2]就已经有理论证明和支撑，由Mercer提出的一系列基于数学证明的理论，即如今的Mercer定理便是这一理论支撑。目前，核方法在许多分类智能算法中都得到了比较成熟的发展，并且已经取得了较为显著的成效，如支持向量机（support vector machine，SVM）[3-5]、核鉴别分析（kernel fisher discriminant analysis）[6-7]等。

在核方法中，因为核函数的多种多样，根据“没有免费午餐”定理（no free lunch theorem，NFL）[8]，任意的单一核函数无法适用于所有的具体任务场景。针对这一问题，Bach等[9]最早提出了多核学习的方法，他们提出的多核学习可以被看作是对核函数的集成学习，但与集成学习不同的是，集成学习针对的是多分类器系统的学习。

如今，对于核方法的研究已经从单核发展到了多核，多核学习（multiple kernel learning，MKL）[10]已是核方法研究的重点。其内容为，当对一个目标样本进行分类时，该目标可能呈现出多种特征，需要从中选取出最适合的特征。多核学习可以把每一种特征都构造成一个单独的子核，然后把这些子核放到一个统一的框架内，从而学习得到最优的子核组合。多核学习的目标就是将多个子核（或称为基核）通过线性组合或非线性组合的学习方法得到一个多核函数（或者是一个多核矩阵，两者只是表达方式不同），其实质就是学习多个核函数的最优凸组合[11]，得到这些特征所形成的单一核的权系数，从而组合成一个多核函数。

现实中，来源于图像、视频、文本等的样本数据大都是上千维或者上万维的高维数据，直接应用到各种算法中会导致所需求的内存过于庞大，并且计算时间也会较长，也就是会出现所谓的“维数灾难”问题。因此对于这些样本数据来说，使用降维方法就是一种必要的手段。

降维就是为了避免产生高维度的维数灾难，以最大限度地保留高维数据的内在信息为前提，将高维数据映射到低维空间中。各种降维的准则形成了各种降维方法。

Lin等[12]在多核学习框架的基础上提出了多核学习降维方法框架，并称之为MKL-DR（multiple kernel learning for dimensionality reduction），它是由多种图像描述子构建多个基核，通过学习得到多个基核的组合权重系数，并将其构造成一个多核矩阵的形式，结合降维方法并最终应用到各种智能算法中。本文的工作便是在其基础上进行的。

近年来，流形学习已是降维领域的又一个研究热点，结合流形学习的思想，即如果将外界的感知表示为高维空间中的点集，而这些感知输入可能会有较强的相关性，可能会在一个低维流形上，或在低维流形的附近[13]，从有限的样本数据中学习到潜在的流形问题从而达到降维目的，因此流形学习对降维有着重要意义。而核函数隐含地通过映射函数将数据投影到高维的特征空间，Lin等可能并未考虑某些隐含映射函数会否改变原数据的流形结构，因此便有了下文将原信息与映射信息结合的构想和尝试。

同一些其他的多核学习的优化方法相比，如丁跃[14]对于多核学习的优化方法是在局部多核学习方法的基础上向目标函数增加正则项，并修改其选通函数的范数形式，解决了选通函数的参数冗余问题，并使之具有更强的泛化能力；奚吉等[15]基于核目标排列准则优化核函数的参数选取，能够同时求解分类器的方程和基核的组合系数，降低算法的时间复杂度。本文的多核学习优化方法着重考虑了流形结构对组合多核的影响，这也恰恰是这些优化算法所没有考虑的，其优点在于能够消除核函数可能产生的扭曲，缺点在于没有准确的方法选择合适的图像描述子，并且受实验环境的影响较大。

2 多核学习降维方法及相关概念

2.1 降维

降维[16]可分为线性降维以及非线性降维。早期的线性降维技术处理的是线性的样本数据，并假设各样本数据点间是相互独立的，使用欧氏距离作为样本点间的相似性度量，这样通过降维方法处理后的低维样本数据同高维样本数据之间是有线性关系的。其中比较有代表性的线性降维方法有主成分分析（principal component analysis，PCA）、线性判别分析（linear discriminant analysis，LDA）。

前面介绍过，大多数的现实样本数据都是非线性的，虽然可以通过某些策略使得线性降维方法近似地处理一些非线性的样本数据，但无法保证其结果，因此随之便出现了许多非线性的降维方法，如核主成分分析（kernel principal component analysis，KPCA）以及核鉴别分析（kernel Fisher discriminant analysis，KFDA）等。本文提到的核方法便是一种解决此问题的有效方法，使用核技巧对线性降维方法进行“核化”[11]就能够使得线性降维方法应用到非线性的样本数据中。

2.2 图嵌入

许多降维方法可以采用图结构来描述样本间的邻接关系，具有简单、直接、有效等特点，具体地说，图嵌入[17]为大多数的降维算法提供了统一的表达形式，即式（1）。使用图嵌入可以将一个降维方法表示为一个完全图G，并且图中所有的顶点构成数据集，设W=[w]∈IRN×N为亲和矩阵，用ij来描述训练集样本间的相似关系，因此亲和矩阵W是一个非负矩阵，并且当xi和xj相邻时，有wij=wji＞0。通过保持样本点间权值的相似性来寻找图在低维空间中的嵌入（又称为映射矩阵）表示，那么，最优的线性嵌入映射v*∈IRd可以由下式获得：

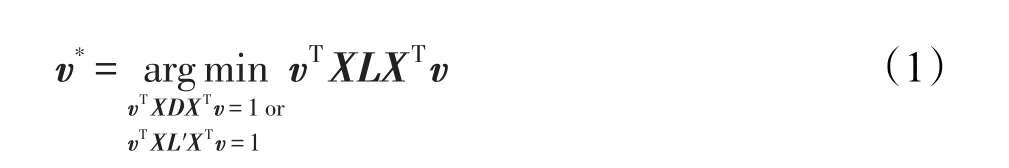
其中，X=[x1x2…xN]是数据集Set的矩阵形式；L=diag(W∙1)-W是完全图G的拉普拉斯矩阵。根据所要解决问题的性质，会从式（1）的两个约束条件中选择一个用于系数优化。若是选择了第一个约束条件，则会在尺度归一化的过程中使用到对角矩阵D=[dij]∈IRN×N，并有D=diag(W∙1)。否则，若是选择了第二个限制条件，需要构造另一个由所有的顶点覆盖数据集Set的完全图G′。其中，L′是完全图G′的拉普拉斯矩阵，W′=[w′ij]∈IRN×N是完全图G′的亲和矩阵。

式（1）的优化问题可以转换成一个更直观的表示：vTX=[vTx1vTx2…vTxN]表示投影，图的拉普拉斯矩阵L（或L′）是投影样本点间的邻接距离，对角矩阵D用于加权地合并投影样本点到原点的距离。更准确地说，式（1）与下面的问题等价：

优化问题（2）的约束条件表明图嵌入模型仅仅需要投影样本点到原点的距离或者是投影样本点间的邻接距离（以vTx表示）。通过改变亲和矩阵W（或W′）和对角矩阵L（或L′）的值，例如PCA、LPP（locality preserving projection）等的降维算法都可以用式（1）表示。

2.3 多核学习

由于特征空间的维数可能很高，甚至是无穷维的，使用映射函数将特征空间中的样本投影到更高的维数是极其困难的，所幸可以使用核方法解决这一问题。

（核函数）对所有x，z∈χ，χ⊂IRn，若有函数k:IRn×IRn→IR满足：

则称函数k为核函数。其中ϕ是从输入空间χ到特征空间Γ的映射，＜，＞表示内积。

使用核函数就不用直接去计算高维甚至是无穷维特征空间中的内积，而且不必关心如何选择映射函数ϕ(x)以及如何实现映射，只需要选择合适的核函数[18]。常见的核函数包括线性核函数、多项式核函数、高斯核函数、拉普拉斯核函数、Sigmoid核函数等。当选择具体的核函数时，若不清楚使用哪个核函数的效果好，则可以先选择高斯核函数进行尝试。

多核学习就是将不同特性的核函数进行组合，以期望能获得多类核函数的优点，得到更优的映射性能。组合的方法多种多样，包括线性组合的合成方法、多核扩展的合成方法等。

本文主要使用了线性组合的方法。下面主要介绍线性组合的方法。设有M个核函数km(x，z)（由于Km(i，j)=km(x，z)，可以使用核矩阵Km的形式表示核函数km(x，z)），通过线性组合可以将几个基核表示成全局核函数k(x，z)（或核矩阵K，原因同上）。

（1）直接求和核

（2）加权求和核

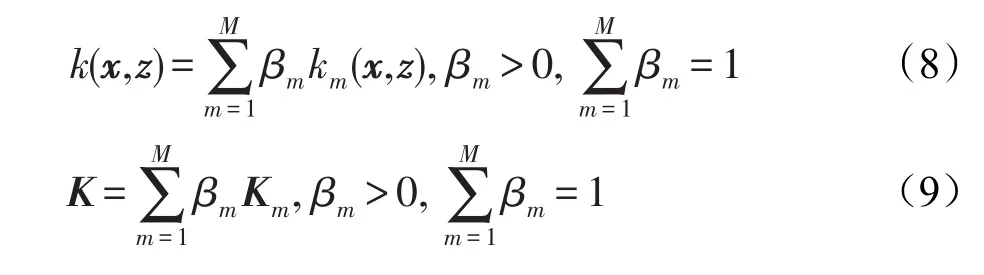
（3）加权多项式拓展核

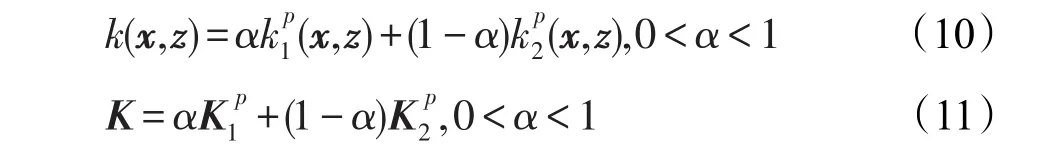
其中，核函数kp(x，z)（或核矩阵Kp）是核函数k(x，z)（或核矩阵K）的多项式扩展。

实际上，SVM算法是一个用于二分类的分类器，对于样本点数据，有xi∈IRd，yi∈{-1，+1}是类标签，那么SVM算法的判别式为f(x)=＜w，ϕ(x)＞+b，通过优化求解则可以得到从而可得：

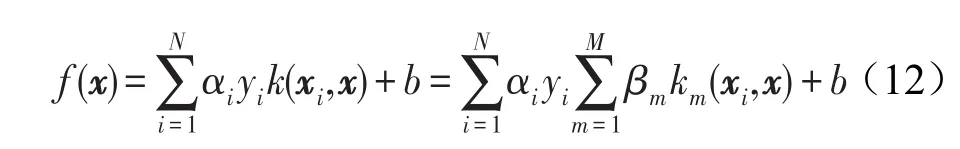
2.4 多核学习降维框架

Kim等[20]提出，在给定的凸集内核中学习得到最优内核并与用于二进制数据的核Fisher判别分析（KFDA）相结合，从而提高核Fisher判别分析的性能。Lin等则在Kim提出的方法基础上考虑通过多核学习来建立各种特征表示数据的维度的一般框架，即多核学习降维框架MKL-DR，这个框架可以应用到有监督学习、无监督学习和半监督学习算法中。本文只将这个框架应用到了有监督学习，无监督学习与半监督学习的降维过程同有监督学习过程是一致的。下面就多核学习降维框架MKL-DR进行详细介绍。

2.5 核函数的选择

设有一数据集Set有N个样本，每个样本由M种描述子表示其特征，令并有dm:χm×χm→0⋃IR+为应用于第m个描述子的距离函数。使用各种描述子会使得数据的表现形式各不相同，Lin等使用核矩阵的形式统一各描述子。通过将数据的特征以及对应的距离函数相结合，就能够得到M个不同的基核矩阵{Km}Mm=1，有：

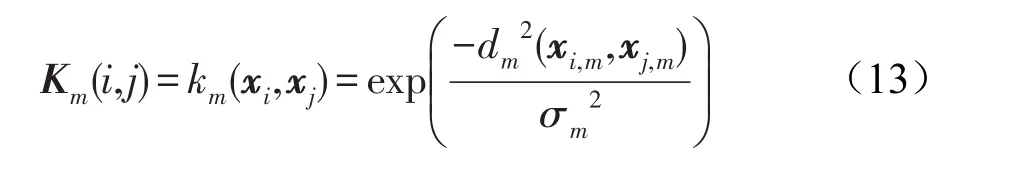
其中，σm叫作带宽，是一个正值常量，对于径向基函数的最终效果有着重大影响。由于采用了描述子以及距离函数，这些基核在处理可视化的学习任务时，会很方便而有效。式（13）中的核矩阵Km并不能保证是半正定的，在处理时，计算核矩阵最小的特征值，如果是负值，则将该特征值的绝对值加到核矩阵的每一个对角线元素上去。获取M个核矩阵后，通过式（8）、式（9）、式（13）就能够求得一组核权重系数的全局最优解 {β1，β2，…，βM}，这组解就是M个由数据特征构造的基核的核权重系数。

这里的径向基核函数会使得数据在特征空间的流形结构扭曲，破坏了原数据的流形结构，因此本文希望能够通过将一部分原信息与特征空间信息结合从而保持原数据的流形结构，以此来达到改善降维效果的目的。

2.6 多核降维算法

多核学习降维中的核化过程同核PCA算法中的核化过程类似，不同点在于多核学习选择的是多个基核的线性组合。

令ϕ:x→Γ表示从低维特征向高维投影空间的映射关系，这个映射关系隐含在核矩阵中，通过ϕ能将训练数据映射到高维的希尔伯特空间。

并且，式（1）、式（2）所表示的问题可以简化为解决XLXTv=λXL′XTv特征值问题，也就是说在映射后的训练集中可以找到这个最优解v，可以表示为：

将映射后的样本ϕ(xi)替换式（2）中的xi，那么投影v将只在vTϕ(xi)中出现。vTϕ(xi)能够通过核方法计算，如下：

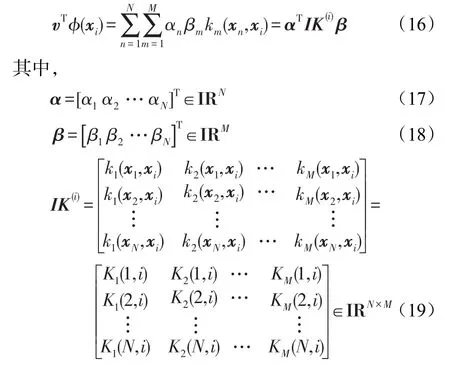
IK(i)是样本xi的核矩阵表示；KM(N，i)是第M个基核矩阵K(N，i)的值。

为了计算方便，先从低维的映射投影代替考虑高维的映射投影，再从低维情况下推广到高维。由式（2）及式（16），可以定义一维空间中的多核学习降维的约束优化如下：

其中，同式（5）、式（6）比较，新增的约束条件式（22）的目的是为了确保组合核的权系数为正数。

由式（16）可以看出，样本系数向量α以及核权重系数向量β决定了一维投影v。为了将其推广到多维的投影中，设有P个样本系数向量，定义为：

每个一维向量投影vi由样本系数向量αi以及核权重向量β决定。最终得到的投影V=[v1v2…vP]将样本投影到P维的欧几里德空间。形如一维的情况，投影后的样本可以写为：

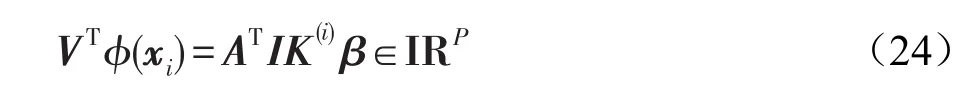
从简单的一维情况推广到多维的情况，那么，优化问题式（20）应用到多维映射投影拓展为下式：

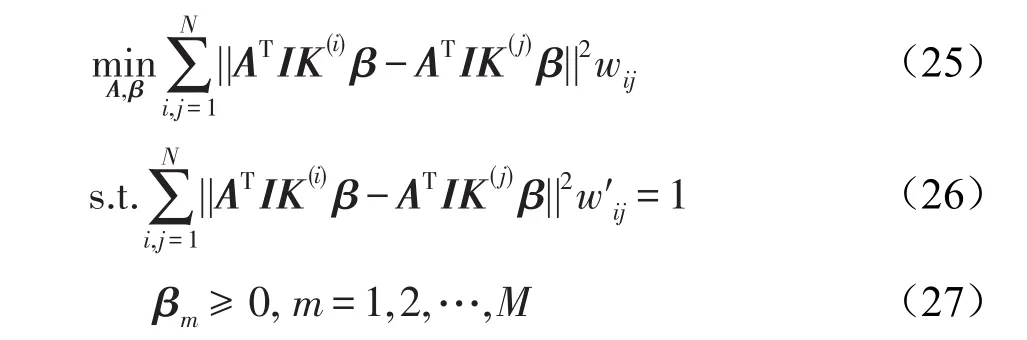
如图1，（a）～（d）依次为每个特征下的输入空间、基核的再生核希尔伯特空间（reproducing kernel Hilbert space，RKHS）、组合核的再生核希尔伯特空间、投影后的欧几里德空间。

3 多核学习优化方法

上文对核函数的选择以及Lin等的相关工作进行了详细的介绍，下文介绍新方法思路和系数优化。

3.1 新方法介绍

式（13）中，核函数km(xi，xj)通过式（5）可以表述为：

其中，ϕ(xi)就是样本xi到高维的希尔伯特空间的投影。

根据原信息与特征信息组合的思路，现将xi按列向量的形式添加到其投影中，有：

Fig.1 4 kinds of spaces in multiple kernel learning for dimensionality reduction图1 多核学习框架中数据在四种空间中的变化示意图

将式（29）代入式（28），并记k′m为新的核函数，可得到：

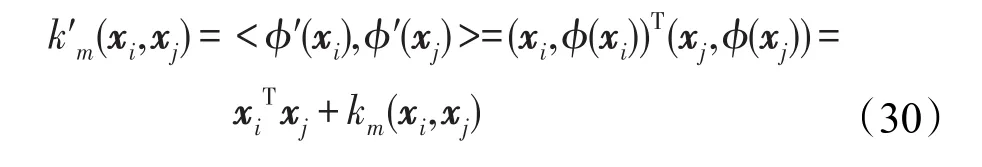
使用现在的核函数k′m代替径向基核函数，并依旧用Km(i，j)=km(xi，xj)表示这个新的核函数k′m，这样上文中优化问题的所有表达式就不需要进行任何改动。

从经验上来说，多核学习中增加了一个新的核函数对其降维效果有正向的作用，其实质就是增加了对数据描述的一个角度，当然，特征的选择要考虑空间和时间效率以及是否必要等方面。

Lin等的多核学习框架中使用径向基核函数能够无限逼近任意的曲线函数。而一个复杂函数会有一个线性部分，因此这里将线性核当作其线性部分。

同时，若将式（30）添加一个加权系数δ，如式（31）。可以观察到，式（31）就是式（11）所表示的加权多项式拓展核的形式。

图2为新的多核函数组合示意图。

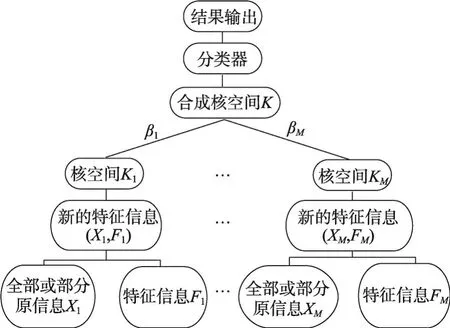
Fig.2 Linear combination of new multiple kernel function图2 新多核函数的线性组合示意图

式（30）、式（31）这种组合是强耦合方式，因此这一对核优化后得到的核权重系数将会是相同的或相关的，并且使用强耦合的方式会由于线性核与径向基核的值域问题可能导致无法得到好的结果。

从上面的思路出发，式（30）若是使用弱耦合的方式则可以表示为：

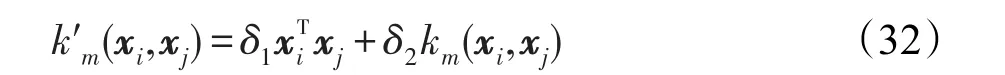
设式（32）所表示的新核函数优化得到其核权重系数βm，则有：

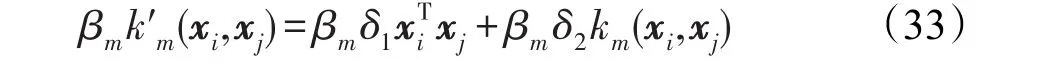
由于式（32）是一种弱耦合，那么可以直接将βmδ1与βmδ2分别表示为线性核权重系数βm1与高斯核权重系数βm2，并可通过下文的系数优化方法得到。

使用线性核能够保持更多原数据的信息量，从而更好地保持原数据的流形结构，那么从式（32）可以看出，其实质就是增加了与高斯核使用相同特征信息的线性核。那么直接使用线性核可以减少从不同角度描述数据所需要的特征信息，即减少了选择的描述子，从而在空间上减少了需要的特征信息。在本文中，减少所需要的特征信息即是缩减了选择的描述子的个数，因此可以省去一部分用于计算图像描述子的时间，提高时间效率。

3.2 系数优化

由于直接优化式（25）是很困难的，可以使用交替优化的方法优化得到A和β。每次迭代固定其中的一个值A或β，然后下次迭代交换为另一个值固定，直到得到的值收敛或是达到最大迭代次数。正常情况下，无法判断值的收敛性，因此需要设置合适的迭代次数。

当优化值A时：固定β并且根据列向量u有||u||2=trace(uuT)，因此式（25）的优化问题可以转化为：

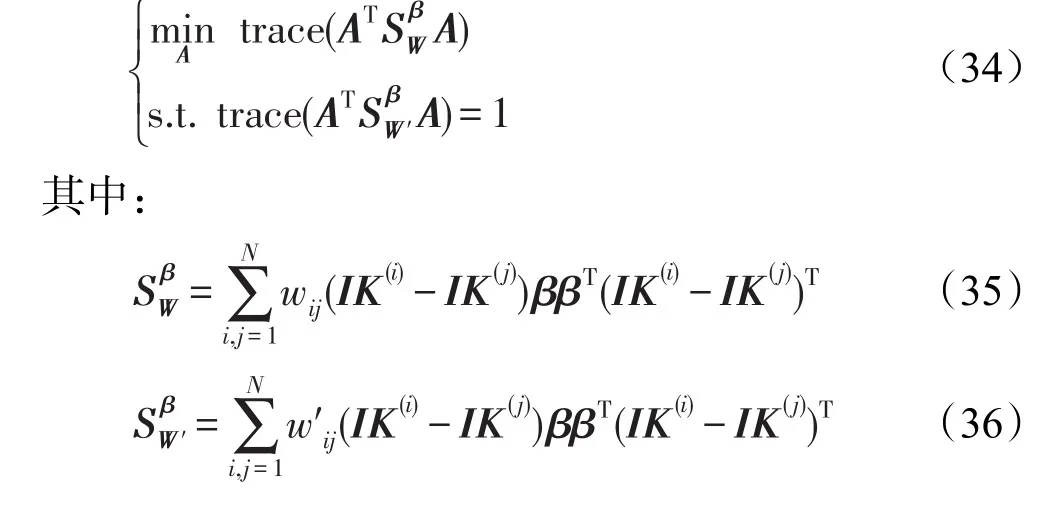
式（34）优化问题是一种迹的比值问题。根据文献[21]及文献[22]，通过将上述问题转化为ratio trace问题，最终可以得到优化的值A*=[α1α2…αP]。其中α1，2，…，P的最优解问题就是求解一个最小化广义特征值问题，取下式前P个最小特征值所对应的特征向量：

当优化值β时：固定A值并且根据列向量u有||u||2=uTu，因此式（25）的优化问题可以转化为：

其中：

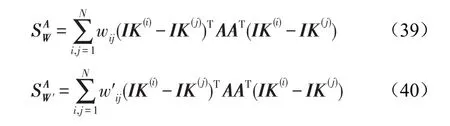
同式（34）比较，新增的约束条件β≥0导致了这个问题不再是广义的特征值问题。实际上，这个问题是一种非凸的二次约束二次规划问题（quadratically constrained quadratic program，QCQP），然而已知的是这个问题是难以解决的，因此使用一种放缩方法，引入大小为M×M的辅助矩阵B，有：

式（43）中的em是第m个元素为1，而其余元素为0的列向量；式（44）是一个半正定约束，也就是指式中的矩阵是一个半正定矩阵。因此式（41）所示的是一个非凸二次约束二次规划问题的半正定放缩求解方法，然后就可以使用已经较为成熟的SDP工具箱求解。其实，令式（44）中的B=ββT就可以看到式（41）等价于式（38）。B=ββT是非凸的，将其放缩为B≽ββT。根据Schur补定理，式（44）等价于B≽ββT（相关推导可以参考文献[23]）。

式（41）中的约束条件是线性的，且其变量个数是关于M的二次式的，一般情况下，取得描述子的个数M都比较小，一般取M=4～10。相对其他的一些降维算法，Lin等提到多核学习降维算法的瓶颈在于如何处理计算复杂度为Ο(N3)的广义特征值问题。

在多核学习降维算法系数优化训练过程的交替优化前，需要选择β或A其中一个变量进行初始化。若是选择β，则令其所有的元素的值相等且其和为1，从而使得所有的基核的权重相等；若选择A，令其满足AAT=I就可以了。从经验出发，选择第二个初始化方法可以得到更稳定的优化结果，本文实验也是选择的首先初始化值β。

3.3 系数优化算法流程

步骤1初始化亲和矩阵W及W′以及基于特征描述子的多个基核

步骤2初始化核权重向量β。

步骤3计算式（35）中的以及式（36）中的，然后通过式（37）对A进行优化求解。

步骤4计算式（39）中的以及式（40）中的然后通过式（41）以及SDP工具箱对β进行优化求解。

步骤5判断是否达到最大迭代次数，未达到则转步骤3；达到则输出核权重向量β以及样本系数向量A。

3.4 测试

设测试样本为z，将其投影到低维空间可以表示为：

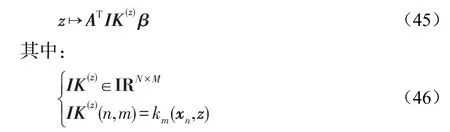
然后采用分类算法中的最近邻法则等对测试数据进行后续的处理操作，从而获得测试数据的新类标签，最终与测试数据的原类标签对比得到分类算法的识别率。

4 实验

本文使用线性判别分析算法（即LDA）展示多核学习降维新方法，实验大部分是基于Lin等的工作，不同之处在于图像描述子的选择与使用。

4.1 数据集

本文实验使用的是由Li等整理的Caltech-101数据集[24]，总共有102个文件夹，对应102个不同的类别，包括101个对象类别（如人脸、蝴蝶、图案等）以及1个背景类别，每个类别包含的图片数量各不相同，最少的为31张，最多的为800张，总共有9 146张图片，每张图片的大小大约为300×200像素。

4.2 图像描述子与基核

本文沿用Lin等所选择的一些特征描述子，再结合本文式（13）所示的径向基核公式形成基核。

GB-Dist：随机从图像矩阵中选取400个边缘化像素，然后用几何模糊描述子处理选择的像素。使用文献[25]中的式（2）所表示的距离函数应用到本文的式（13）生成一个基核。

GB：与GB-Dist描述子的不同点就是没有使用几何模糊描述子而直接用对应的距离公式构造基核。

SIFT-Dist：和GB-Dist构造基核的过程一样，只是使用了SIFT描述子代替GB描述子。

SIFT-SPM：将3个不同尺度的SIFT描述符应用于每个图像的均匀采样网格，并从所有图像的局部特征使用k均值聚类生成视觉词。然后，基核通过文献[26]中的匹配空间金字塔来构建。

SS-Dist/SS-SPM：这两个基核的构造和SIFT-Dist/SIFT-SPM相同，只是使用self-similarity描述子代替SIFT描述子。其中，设置self-similarity每一块的大小为5×5，窗口半径为40。

C2-SWP/C2-ML：使用文献[27]中的C2特征描述子及文献[28]中的C2特征描述子，能够获得高斯基核。

PHOG：限制pyramid level为2，并使用距离公式χ2。

GIST：首先将图片的图像大小调整为128×128像素，再使用GIST描述子生成一个高斯基核。

上面介绍的图像描述子中的参数以及对应使用的距离函数是相互独立，即基核是相互独立的。

Lin等的实验选择了上面的10个基核进行多核学习，本文则在其基础上进行了相近的实验，不同的是分别使用了4～10个基核，用于同单核学习以及本文的新方法进行对照。

从上述的图像描述子的介绍中可以看到，类似GB与GB-Dist、SIFT与SIFT-Dist等这样的基核，仅仅在图像描述子的使用方法和距离函数的使用上不同，使用的描述子是相同的。新方法中，使用线性核与高斯核结合的方式，则可以描述为在这一对图像描述子中选择一个较合适的来生成线性核与高斯核。

4.3 降维方法

LDA算法要求数据集全部要带有标签，并且数据要保持高斯分布。下文的实验中，为了区分本文所做的优化方法与Lin等的MKL-LDA（multiple kernel learning-lineardiscriminantanalysis）算法，将本文的优化方法简记为MKL-LDAOPT，其使用的亲和矩阵为：

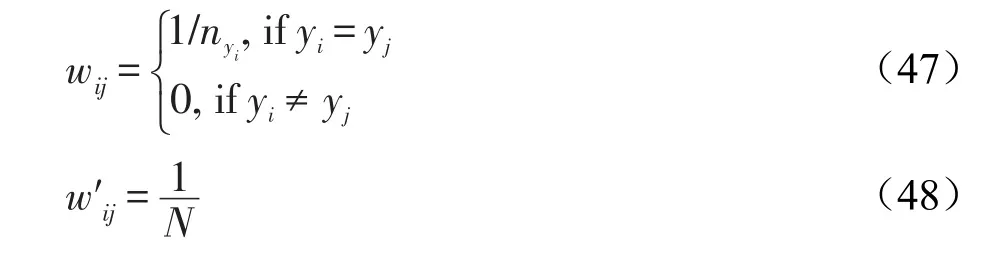
其中，nyi是拥有相同标签yi的个数。

4.4 参数设置

Caltech-101数据集总共有102个类别，对应设置为102个类标签，由于每一类的图片个数各不相等，最少的为31张，最多的为800张，因此统一取整为每类取样30张图片。将这102×30个样本分割为训练集与测试集，设每一类取到的训练样本个数为Ntrain，则测试集样本个数为30-Ntrain。实验中取Ntrain分别为5、10、15、20、25，并且为了消除取样造成的影响，在不同的训练样本个数Ntrain下重复20次实验取平均值，每次实验随机选取训练样本以及测试样本。

对于式（13）高斯核函数中带宽参数σm的初始化设置是较难寻到最优值的，一般是从经验角度出发，通过设置一些特殊值，如[0.001,0.01,0.1,0.5,1,1.5,2,5,10,15]等试验性地进行寻参。这里将采用另外一种策略，根据Km前Ntrain列的和与其余列的和的比值来确定最终的σm值。

下面是确定带宽参数的算法步骤：

步骤1通过经验初始化一组σm的取值范围以及期望值，左右界分别记为left和right。

步骤2令σm的值为(left+right)/2。

步骤3计算核矩阵Km，获得Km前Ntrain列的和与其余列的和的比值ratio。

步骤4通过步骤3得到的比值ratio判断移动左右界，若比值ratio大于期望值，令left=(left+right)/2；反之则需要移动右界，令right=(left+right)/2。

步骤5判断有无越界，比值ratio与期望值之差小于某一阈值以及是否达到最大的迭代次数，若为假则转到步骤2，否则退出迭代，并且输出σm，那么就得到了一个全局较优的σm值。

4.5 结论分析

基于LDA分类算法的单核学习降维算法与多核学习降维算法的识别率如表1、表2所示。表2的MKL-LDAOPT实验中，当图像描述子个数M=4时，则使用的图像描述子为GB、SIFT-SPM、SS-SPM、GB-SPM；当图像描述子个数M=5时，则使用的图像描述子在表2中依上而下分别为GB、SIFTSPM、SS-SPM、C2-SWP、GIST和GB、SIFT-SPM、SS-SPM、C2-SWP、PHOG；当M=6时，则使用的图像描述子为GB、SIFT-SPM、SS-SPM、GB-SPM、GIST、PHOG。

为了同MKL-LDA OPT的结果进行对比，表2中MKL-LDA的描述子个数M=4，5，6 时 ，同 MKLLDA OPT所选择的描述子是相同的，当MKL-LDA的描述子个数M=7，8，9，10 时，则是依表1中的描述子从上至下逐个增加进行实验所得。

从图3中可以看出，由实线代表的多核学习降维方法的识别率明显优于由虚线代表的单核学习降维算法的识别率，验证了多核学习的优越性。同时单核学习的实验结果也能够证明在选择图像描述子时并非其效果越好，则在多核学习中使用效果就越好。

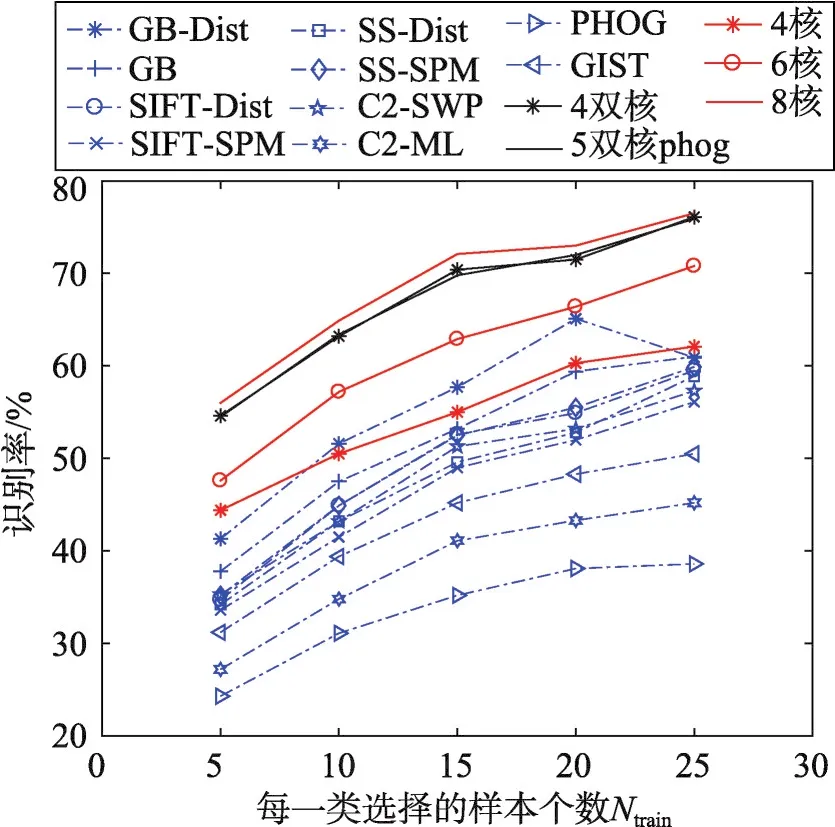
Fig.3 Recognition rate of SKL-DR and MKL-DR，MKL-DR OPT图3 单核学习降维与多核学习降维的识别率

在表2和图4中，MKL-LDA OPT的实验结果与MKL-LDA的实验结果相比较，可以观察到二者使用的图像描述子个数M都为4或5时，新方法的识别率已经有了明显的提高。

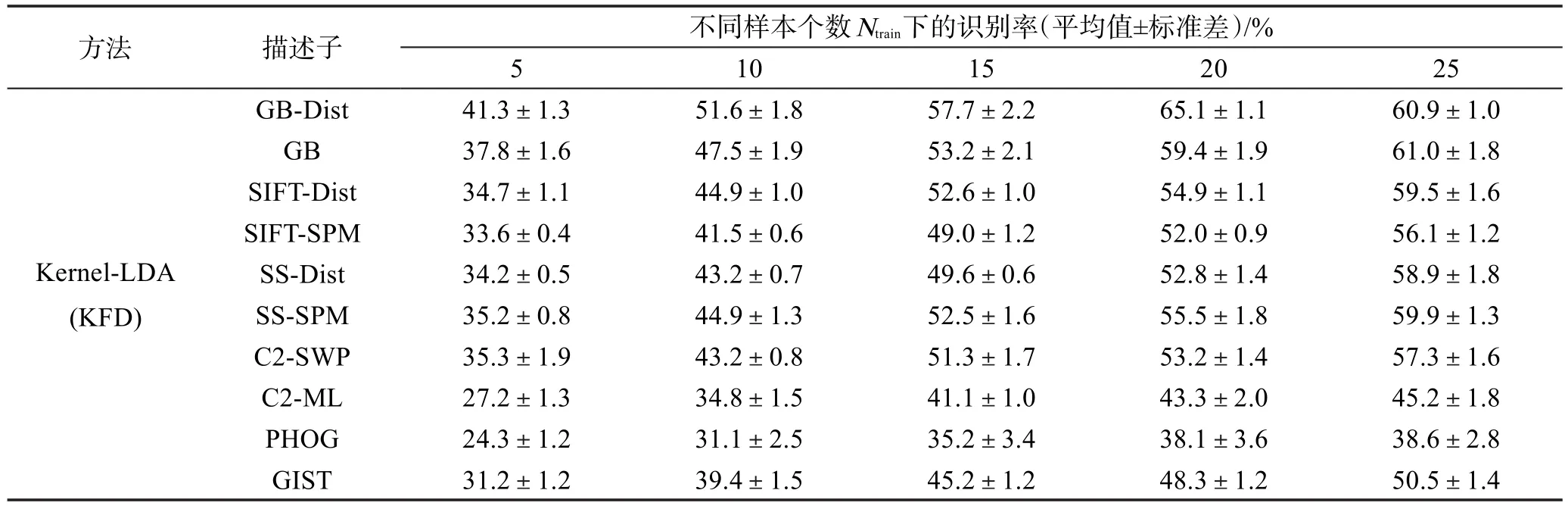
Table 1 Recognition rates of LDA-based classifiers on single kernel learning for dimensionality reduction algorithm表1 基于LDA分类算法的单核学习降维算法的识别率

Table 2 Recognition rates of LDA-based classifiers on multiple kernel learning for dimensionality reduction algorithm表2 基于LDA分类算法的多核学习降维算法的识别率

并且在图4中，3条实线同另外的3条虚线非常贴合，表示使用新方法选择了4或5个图像描述子就几乎能够达到Lin等的方法选择了7或8个图像描述子时达到的算法识别率。

同时，可以看到在MKL-LDA的实验结果中，当M=8时，其结果（即算法识别率）同M=9和M=10的实验结果相比几乎没有太大的提高。这也正如上文所说的，并不是选择了越多的特征其描述越好。同时，本文新方法的实验结果也同MKL-LDA的情况一样，当M=6时，算法的识别率同M=5时的结果相比并未提高，并且可以对照当M=5时，算法识别率有较大的差异。

Fig 4 Recognition rate of MKL-LDA and MKL-LDAOPT图4 MKL-LDA与MKL-LDAOPT的识别率

5 结束语

本文引入流形学习的概念，并通过实验证明了将原信息与特征信息进行组合的方法是有效的，并且减少了原方法所要选择使用的图像描述子的数量。同时计算每一个图像描述子并构建基核是很耗费时间的，因此同达到的算法效果相同的原方法相比，减少图像描述子能够明显缩短算法的运行时间，从而在实际应用中能够提供一种更高效的思路。

文中使用原信息的全部信息与特征信息组合的方法并不好，因为使用原信息的一些局部信息就能够保留其流形结构，而不需要所有的信息，这样就会减少样本的冗余，提高算法的时间效率。并且，文中第一次提到的线性核与高斯核的加权多项式拓展核的形式也不失为一种好的方法，不过需要找到一组合适的参数。

本文下一步将尝试通过引用深度学习与流形学习相结合的思路对多核学习降维方法进行优化。