交叉极化干扰对阵列雷达测角影响研究

王海军，戴幻尧，聂孝亮，刘海业

(中国洛阳电子装备试验中心，河南 洛阳 471003)

0 引 言

电子对抗(ECM)[1-2]是一种特殊作战手段，是现代战争不可缺少的作战力量，可以以多种方式运用于战略威慑、作战支援、武器平台自卫、阵地防护和反恐维稳等战略、战役和战术行动中。角度测量[3]是实现目标探测[4]、定位、跟踪和制导的关键环节，是有效实施电子对抗手段的前提。

采用极化融合单脉冲测角方法的极化[5]阵列雷达(Polarization Array Radar, PAR)可以实现目标角度的精确测量[6-7]，在电子对抗中发挥着重要作用。PAR在抗干扰、目标识别、成像等领域明显优于传统单极化阵列雷达，是一种重要的新体制雷达[8]。PAR充分利用了阵列雷达抗干扰能力强、多目标分辨力高的优点，并能够利用目标的极化信息[9]，进一步提高目标角度测量精度。极化融合[10]单脉冲测角方法是对单脉冲测角方法的改进，对H极化通道和V极化通道测量结果进行加权融合，得到最终测量角度，测角性能优于传统单脉冲测角方法。由于极化融合单脉冲测角阵列雷达采用了阵列天线、极化融合技术等手段，使得其对传统的单极化压制干扰和角度欺骗干扰具有很强的抗干扰能力[11]。交叉极化干扰[12]是利用雷达天线主极化与交叉极化接收矢量之间的不一致性[13-14]，发射与雷达工作频率相同、极化与雷达天线主极化正交的电磁波去照射雷达，从而达到角度欺骗的目的，是一种新型的干扰手段[15]。由于交叉极化干扰不要求具备在空间上分离的多个干扰源，使得其对于重要目标防护或导弹突防方面具有极大的应用潜力[16]，被广泛认为是对付单脉冲测角雷达的有效技术手段。

当存在交叉极化干扰时，极化融合单脉冲阵列雷达的测角性能会受到影响。本文研究证明，交叉极化干扰对极化融合单脉冲阵列雷达的测角性能有较大影响，影响大小取决于交叉极化干扰强度及目标回波极化特性。

1 极化融合单脉冲阵列雷达测角方法

极化阵列天线采用由双正交偶极子对构成的均匀线阵，有N=16个阵元，阵元间距为半个波长d。设定阵元沿Y轴均匀排列，两个正交偶极子分别沿X轴和Y轴排列，X轴为水平极化方向，Y轴为垂直极化方向。为方便讨论，这里只考虑俯仰方位向的一维角度测量，限定回波位于YOZ平面，即方位角φ=π/2，俯仰角θ∈[-π/2, π/2]，如图1所示。

图1 极化阵列天线结构示意图

Fig.1 Polarization array antenna structure

该极化阵列雷达可以看成一个水平极化阵列雷达和垂直极化阵列雷达的组合，极化融合的思想是将这两部单极化阵列雷达分别进行单脉冲测角，根据单脉冲测角原理和最大似然估计理论，得到两种正交极化对应的角度测量值和幅度估计值，然后将两组数据加权融合得到最终测角结果。需要说明的是，在进行单脉冲测角时，将16个阵元平均分配，从而得到目标的和差信号。阵列雷达极化融合单脉冲测角方法如图2所示。

将一维线阵平分为两个子天线阵后，这两个天线阵波束指向一致，得到两个一样的接收波束，只是相位中心间距D=d·N/2，两波束接收信号幅度相等，相位相差Δφ=sinθ·2πD/λ。两波束输出信号为E1和E2，则E2=E1·e-i·Δφ。根据单脉冲测角原理，通过计算差和比Δ/Σ=(E1-E2)/(E2+E1)，即可提取目标的角度信息，其测角公式为

(1)

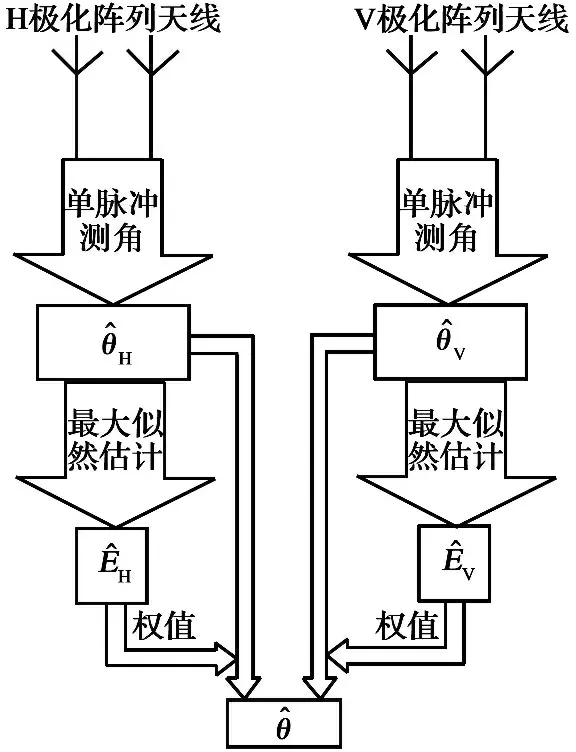
图2 阵列雷达极化融合单脉冲测角方法

Fig.2 Polarization-intergration mono-pulse angle measurement method of array radar

(2)

接收信号与复幅度的联合概率密度函数为

(3)

根据最大似然函数方法，可得到接收信号的复幅度估计值为

(4)

(5)

(6)

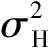
(7)

其中：k2=0.19N/(N2-1)为常数；θ3 dB为3 dB波束宽度，得到最终角度估计值:

(8)

2 对极化融合单脉冲阵列雷达的交叉极化干扰方法分析

极化阵列雷达采用双极化工作模式，发射水平极化波，同时接收水平极化波和垂直极化波，然后采用极化融合方法进行角度测量。从目标处发射垂直极化波对极化阵列天线进行干扰，虽然垂直极化通道的信噪比得到增强，测角更加准确，但是，水平极化通道由于交叉极化干扰的存在，测角的误差增大。两个通道融合后的测角误差可能增大，使得极化融合算法失效。

极化阵列天线可以看成一个水平极化阵列天线和一个垂直极化阵列天线的组合，进行单极化测角时每个单极化阵列天线又均分为两个子阵，这样就存在四个子阵，每个子阵对应一个主极化波束和交叉极化波束。

假设四个子阵的主极化幅度方向图和相位方向图都是一致的，即

GH1m(θ)=GH2m(θ)=GV1m(θ)=GV2m(θ)=Gm(θ)

PH1m(θ)=PH2m(θ)=PV1m(θ)=PV2m(θ)=Pm(θ)

其中：GH1m(θ)和GH2m(θ)分别为水平极化阵列天线两个子阵的主极化幅度方向图函数；GV1m(θ)和GV2m(θ)分别为垂直极化阵列天线两个子阵的主极化幅度方向图函数；PH1m(θ)和PH2m(θ)分别为水平极化阵列天线两个子阵的主极化相位方向图函数；PV1m(θ)和PV2m(θ)分别为垂直极化阵列天线两个子阵的主极化相位方向图函数。为方便研究，可以设置Pm(θ)=0°，即两个主极化波束接收的回波不存在天线引起的相位差。

不同天线的交叉极化幅度方向图和相位方向图很难做到一致，设水平极化子阵和垂直极化子阵的交叉极化幅度方向图分别为GH1c(θ)，GH2c(θ)，GV1c(θ)，GV2c(θ)；相位方向图分别为PH1c(θ),PH2c(θ),PV1c(θ),PV2c(θ)，则水平极化阵列天线得到的差信号为

ΔH=ΔHm+ΔHc=Gm(θ)·EH(1-e-jΔφ)+GH1c(θ)·PH1c(θ)·(EV+EiV)-GH2c(θ)·PH2c(θ)·(EV+EiV)·e-jΔφ

(9)

和信号为

ΣH=ΣHm+ΣHc=Gm(θ)·EH(1+e-jΔφ)+

GH1c(θ)·PH1c(θ)·(EV+EiV)+GH2c(θ)·PH2c(θ)·(EV+EiV)·e-jΔφ

(10)

同样，垂直极化阵列天线得到的差信号为

ΔV=ΔVm+ΔVc=Gm(θ)·(EV+EiV)·(1-e-jΔφ)+GV1c(θ)·PV1c(θ)·EH-GV2c(θ)·PV2c(θ)·EH·e-jΔφ

(11)

和信号为

ΣV=ΣVm+ΣVc=Gm(θ)·(EV+EiV)·

(1+e-jΔφ)+GV1c(θ)·PV1c(θ)·EH+

GV2c(θ)·PV2c(θ)·EH·e-jΔφ

(12)

考虑交叉极化分量存在时，水平极化和垂直极化接收到的信号为

(13)

其中:s(θ)=[ejφ1ejφ2… ejφN]是相位加权矢量;s1(θ)=[ejφ1ejφ2… ejφN/2]和s2(θ)=[ejφN/2+1ejφN/2+2… ejφN]分别是两个子阵的相位加权矢量。

3 仿真分析

子阵的主极化方向图采用辛格函数进行模拟：

Gm(θ)=[sin(kmθ)/(kmθ)]2

(14)

子阵的交叉极化幅度方向图采用辛格函数一阶导数的变体函数进行模拟，具有多个控制参数，可实现对交叉极化方向图的灵活模拟：

(15)

式中：kc的值由[0, π]内旁瓣数目决定；L为衰减调节量，可根据需要设定；α,β为波束形状参数；θ为相应的角度值，单位为rad。式(14)采用km=40，则波束宽度为θ3 dB=4°。水平极化阵列天线两个子阵交叉极化幅度方向图设置为kH1c=39，LH1c=32，αH1c=1.8，βH1c=1.5,kH2c=40，LH2c=32，αH2c=1.4，βH2c=2；垂直极化阵列天线两个子阵交叉极化幅度方向图设置为kV1c=35，LV1c=33，αV1c=1.2，βV1c=2，kV2c=30，LV2c=30，αV2c=2，βV2c=2。

交叉极化的相位方向图目前还没有有效的数学模型进行模拟，并且随机性较大，本文采用一组固定的随机数对子阵的交叉极化相位方向图进行模拟，在仿真分析中每个子阵对应的一组随机数保持不变。

图3给出了各子阵的主极化和交叉极化幅度方向图，从图中可以看出在主瓣内交叉极化的幅度明显低于主极化幅度，约低20 dB左右，与天线的实测数据相符。各个子阵的交叉极化幅度方向图也存在较大差异，提供了交叉极化干扰有效实现的物理条件。

图3 各子阵的主极化和交叉极化幅度方向图

Fig.3 Main polarization and cross-polarization amplitude patterns of subarrays

3.1 测角性能与交叉极化干扰强度关系

图4给出了极化阵列雷达测角精度与交叉极化干扰强度的关系，并与无干扰情况进行了对比，在交叉极化干扰强度在-10～10 dB范围内，存在干扰的测角精度要劣于无干扰情况。图中无干扰情况下垂直极化阵列测角精度曲线没有显示，因为目标回波的垂直极化分量很小，且目标回波的水平极化分量对其形成交叉极化干扰，使其测角偏差较大，失去了对比意义。从图4可以看出，当存在交叉极化干扰时，随着干扰强度的增大，水平极化天线测角性能逐渐降低，垂直极化天线测角性能逐渐增强。当交叉极化干扰强度较小或者较大时，由于水平极化和垂直极化天线测角性能差异明显，所以极化融合之后接近于高性能一方，干扰效果不明显。当交叉极化干扰强度与目标回波的主极化分量到达天线口面处强度相近时，主极化阵列天线的测角性能下降程度大于交叉极化阵列天线测角性能改善程度，经过极化融合之后，双极化阵列雷达整体测角性能下降。经过对图4和表1仿真数据的分析可知，交叉极化干扰可使阵列雷达测角性能最大下降10%左右。

图4 测角精度与交叉极化干扰强度关系

Fig.4 Relationship between measurement accuracy and cross-polarization interference intensity

3.2 测角性能与目标回波极化比关系

不同目标的极化散射矩阵是不同的，通常用目标回波极化比[17]对目标的交叉极化分量与共极化分量的关系进行描述。本节主要研究目标回波交叉极化分量大小对交叉极化干扰效果的影响，所以设置φ=φc-φm=0°。其中，φc和φm分别为目标回波交叉极化分量与共极化分量的相位。用dB形式表示的目标回波极化比为

(16)

式中：Ec为目标回波的交叉极化分量；Em为回波的共极化分量。

进过仿真分析，可得目标回波极化比ρcm和对应的最佳交叉极化干扰强度jopt及性能最大下降幅度dmax三者关系如表1所示。

表1 阵列雷达测角性能下降率与目标回波极化比的关系

Table 1 Relationship between decrease of angle measuring performance of array radar and polarization ratio of target echo

ρcm/dBjopt/dBdmax/%-24-110.9-22-110.6-20-110.4-18-210-16-29.2-14-38.4-12-37.2-10-35.7-8-64.1-6-72.6-4-91.3-2-110.30-150

从表1中可以看出，对极化融合阵列雷达的交叉极化干扰效果与目标回波的极化比密切相关，回波的极化比越小，交叉极化干扰越大，雷达测角性能下降率越大，即目标回波的交叉极化分量越小，交叉极化干扰越明显。交叉极化干扰功率略小于目标回波的共极化分量功率，对实施干扰的条件要求较低，便于在各种对抗环境下灵活实施。从表中可以看出，当目标回波的交叉极化分量明显小于共极化分量时，交叉极化干扰效果显著，阵列雷达的测角性能下降10%左右，严重影响雷达对目标角度的有效探测。

需要说明的是，采用极化融合单脉冲方法测角的极化阵列雷达具有非常强的抗干扰能力，图4中干扰情况下的两条单极化测角曲线的交点在无干扰极化融合测角曲线之上，说明交叉极化干扰对该种体制的雷达是具有一定干扰能力的，可使雷达的测角性能下降但不会完全失效。

经过以上仿真分析可知，极化融合单脉冲阵列雷达受到交叉极化干扰时，测角性能会受到一定影响，影响程度与被测目标的回波极化特性密切相关，回波的极化比越小，测角性能下降越大。

4 结 论

在复杂的电子对抗环境下，雷达会受到多种干扰，有效分析干扰对雷达性能的影响是雷达正常工作及采取有效应对措施的前提。本文研究了交叉极化干扰对极化融合单脉冲阵列雷达测角的影响，首先阐述了阵列雷达极化融合单脉冲测角方法，包括单极化单脉冲测角、复幅度估计和极化融合三个关键环节。然后对极化融合单脉冲阵列雷达的交叉极化干扰方法进行了理论分析，从数学上证明了该干扰方法可带来极化融合测角的误差项，导致测角精度下降。最后，对四组子阵的主极化及交叉极化天线方向图进行了仿真模拟，并在此基础上对极化阵列雷达的测角性能进行了交叉极化干扰仿真，得到了RMSE随交叉极化干扰强度的变化曲线及RMSE与目标回波极化比的关系。仿真结果表明，交叉极化干扰会导致阵列雷达测角性能的下降，目标回波的极化比越小，即目标的交叉极化分量越小，雷达受干扰越明显，测角性能下降越大，性能降低10%左右。本文研究了交叉极化干扰对极化融合单脉冲阵列雷达测角影响的大小，对其中的主要因素即交叉极化干扰强度和目标回波极化比进行了仿真分析，对电子对抗环境下雷达性能受影响程度分析有一定指导意义。