基于Keystone变换与Dechirping补偿的雷达运动目标检测跟踪算法研究

陈 杰，赵英潇，吴 琪，张 月

(国防科技大学 ATR重点实验室，长沙 410073)

0 引 言

现代战争中，随着高速飞行器技术的进步和隐身目标的发展，作战飞机、无人机在内的航空飞行器以及巡航导弹等高速飞行物的飞行速度不断突破极限，这对需要足够信噪比才能检测目标的传统雷达来说，发现和测量远距离、低可探测、高机动目标的难度越来越大。要想在不改变雷达基本参数的情况下提高对微弱目标的探测能力，利用先进的信号处理方法——长时间积累检测，是一种行之有效的解决途径。该方式灵活多样，成本较低，对射频前端的要求较低，使雷达后期的升级周期和复杂度大大降低，具有重要的实际意义[1]。然而，应用传统雷达信号处理手段对运动目标进行长时间积累时会遇到两大问题。一是因目标高速运动和雷达系统高距离分辨率之间的矛盾。在进行长时间积累时，目标的回波包络会跨越多个距离单元，也就是距离徙动现象(ARU)，该现象会随着目标速度的提高和积累时间的增多而越来越明显。二是因目标加速度或者更高阶运动而导致回波在距离-时间域内呈曲线关系。随积累时长增加，多普勒频率表现出时变特性，即跨分辨率单元的多普勒频率扩展(DFM)。这两个问题极大地降低了雷达相干积累的增益。

针对包络走动问题，1998年，Perry R P等[2]提出了用Keystone变换设定了一个中间变量——虚拟时间，来解除快时间频率与慢时间的耦合关系，从而消除目标回波中的线性位移项。另外还有SCIFT法[3]、ACCF法[4]等也被提出用于包络走动补偿，但应用最广泛的主要还是Keystone变换法。

针对多普勒走动问题，根据Weierstrass近似原理，多项式相位信号能够很好地与雷达目标回波信号近似匹配[5]。通常情况下，对目标回波取一阶近似，表现为二阶PPS信号，也就是所谓的线性调频信号(LFM)，对LFM信号进行参数估计然后进行多普勒走动补偿，是一种主流思路。针对PPS信号相继涌现出一些参数估计方法，如离散Chirp-Fourier变换法、时频分析法和降维参数估计法等。对于时频分析法，1990年，Barbarossa S和Farina A提出了用时频分析法中的WVD来检测运动目标[6]。基于分数阶Fourier变换的相参积累方法是一种时频平面的旋转变换，其利用离散分数阶傅里叶变换，对每个多普勒单元在进行二次相位补偿的同时也进行了相参积累，以增强雷达在强杂波背景下对微弱运动目标的检测能力[7]。上述方法大都需要通过映射到特定的变换域上实现，无论是构造相位补偿函数还是变换到特定域，其运算量都是只增不减。为了平衡运算量与估计精度之间的矛盾，还出现了一些流程改进的方法：有多次精度递进式估计方法、逐次估计回波参数方法[8]；也有对目标加速度进行先粗后细的估计补偿方法。

国内在雷达微弱目标长时间积累检测技术也取得一些显著成果。许稼等提出了一种基于检测前聚焦的雷达隐身目标探测算法，该算法引入Radon-FFT变换的思想，通过遍历搜索目标参数空间的方式，无需多普勒解模糊便可解决距离徙动与相位调制耦合的问题[9]。陈小龙等提出基于Radon-FFT变换和分数阶傅里叶变换相结合的算法，能够有效补偿距离和多普勒走动，实现高积累增益和抑制杂波与噪声的目的[10]。吕小磊提出一种对多项式信号参数进行估计的算法——Lv’s Distribution(LVD)[11]，该算法能够解决时频分析中交叉项与分辨率之间的矛盾，并相继提出了利用Keystone变换和Radon-Fourier Transform(RFT)算法进行距离徙动校正后，再用LVD方法从雷达回波中估计目标运动参数的检测估计方案，该方法还可用于多目标检测和运动参数估计[12]。

1 算法描述

1.1 基于Keystone变换的校正补偿

对回波信号进行脉冲压缩处理后的时域表达式为

(1)

由式(1)可以看出不同脉冲回波包络峰值位置的走动。因此，定义虚拟时间ηm与tm之间存在尺度变换的关系：

(2)

式中：ηm=mT′，T′为脉冲重复间隔，对应虚拟慢时间。将式(2)代入式(1)得

(3)

1.1.1 Keystone变换的实现方法

与tm对应的表达式中，频谱采样点的位置在单位圆上的分布间隔变为[(f+fc)/f]·(2π/M)，其间隔不是均匀分布在圆周上的，无法利用快速傅里叶变换进行计算，而Chirp-Z变换则是针对上述非等间隔情况下的快速算法。

假设有限长序列x(n)(0≤n≤N-1)，其中Chirp-Z变换可以表示为

(4)

式中：A=A0ejθ0,W=W0e-jφ0,A0表示起始抽样点z0的矢量长度，W0表示螺旋的伸展率，θ0表示起始抽样点的相角，φ0表示相邻两个抽样点之间的角度差；N为快时间采样总数；M为一个相参积累时间内的积累周期数。

因此，Keystone变换借助Chirp-Z变换的方法实现公式如下：

(5)

1.1.2 多普勒解模糊的方法

实际应用中，当目标飞行速度较大时，会出现速度模糊现象。下面研究多普勒解模糊的方法。

当目标的速度v≥λfr/2时，令多普勒频率为

fd=fd0+F/Tr

(6)

式中：fd0为模糊多普勒频率；F为模糊数；Tr为脉冲重复周期。

式(6)经过Keystone变换后变为

2v(fc+f)/c=fd+Ffc/Tr(fc+f)

(7)

因此，需要考虑相位补偿项：

C(F,m)=exp[-j2πmFfc/(fc+f)]

(8)

本文解模糊采用的方法是并行搜索方法，即对Keystone变换的结果与多个相位补偿项进行并行搜索相乘，当进行搜索的补偿相位项恰好与目标的多普勒模糊数一致时就会出现最大值，即

(9)

从而在完成各距离频率单元的相位补偿的同时完成多普勒解模糊。

1.2 多通道Dechirping补偿

实际中，绝大部分运动目标在积累时间内的运动方式还是可以近似成匀加速运动。匀加速目标的回波在经过距离单元走动校正之后，其回波多普勒相位随慢时间变化可近似为二次曲线，即多普勒频率不再是一个点频，而是一个LFM信号。由于实际探测中无法得知加速度的先验信息，因此可采用多通道搜索方式，遍历加速度可能的范围，采用多通道Dechirping方法对加速度引起的二次相位项进行有效补偿。

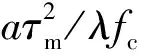
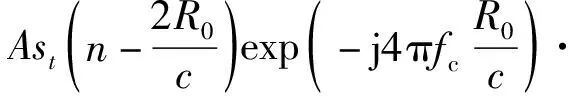
(10)

第n个距离单元第l个加速度补偿通道输出为

(11)

对式(11)进行慢时间维FFT，得到第n个距离单元第l个加速度补偿通道的积累结果。对每个距离单元进行处理得到一个L×M二维矩阵。该处理流程比常规MTD处理多增加了一维信息，积累时间越长，频谱分辨率越高，可更好地区分多目标。

1.3 基于AR模型的卡尔曼滤波算法

由于目标运动模型的不确定性，一个完整的目标跟踪滤波器将包括多个运动模型，其中经典的跟踪模型有匀速(CV)模型和匀加速(CA)模型等。但是，实际目标在运动过程中一旦加速度发生变化或进行更加复杂的机动变化，单个CV或CA模型会与当前状态不匹配，从而使误差变大，因此，需要根据目标实际运动情况自适应地切换目标运动模型。不同阶数的AR模型可以描述目标不同的运动模式[13]。

卡尔曼滤波器利用一段时间内对目标状态的观测，采用迭代递推计算的方式，实现对系统状态的最优估计。随着观测值的不断累积，可实现对目标状态的连续跟踪[14]。

2 实验结果验证

2.1 Keystone变换结果

比赛给定的雷达数据为地面背景下空中固定翼无人机目标的时域回波数据，由安装于二轴转台上的试验雷达获取得到。雷达工作模式为宽带距离-多普勒模式，输入数据为脉冲压缩后的时域脉冲序列。试验雷达的载频为35 GHz，脉冲重复频率为32 kHz。对于快时间维(每个脉冲)，距离采样单元的间隔为1.875 m，距离波门长度固定(含319采样点)，波门起始位置(对应第1个采样点)随目标移动，更新率为1 ms(32个脉冲更新一次)。图1给出了经FFT后的1帧R-D图像。

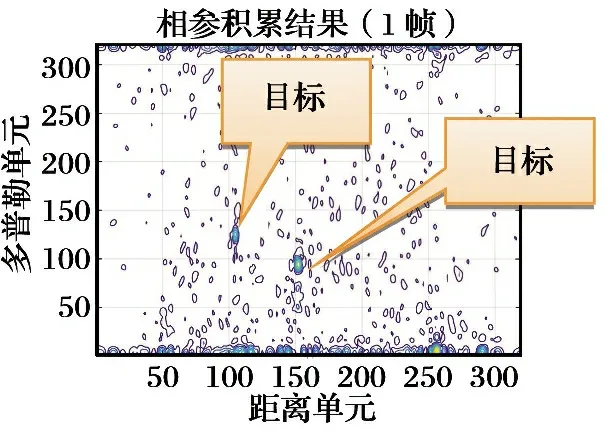
图1 两个目标的R-D图像示例

Fig.1 An R-D image example of two targets

可以看出，目标回波能量在积累中发生了扩散，无法聚焦在同一单元格内，并且在积累平面中杂波占据了大半部分位置，对目标的检测跟踪造成了很大的困难。Keystone变换前的图像如图2所示。随着积累时间的增加，目标回波能量跨越的距离单元越多，能量聚焦的效果就越差。

图2 原始脉压结果

Fig.2 Original PC results

Keystone变换后的图像如图3所示，距离徙动得到了有效校正。此时再对目标回波能量进行积累，目标回波的能量就不会扩散到多余的距离单元中。虽然距离徙动得到校正，但是由于目标运动的加速度引起的多普勒走动在进行相参积累后的结果中还是存在的，需要对其进行Dechirping相位补偿以校正多普勒走动。

图3 Keystone变换后图像

Fig.3 Keystone transformed image

2.2 Dechirping补偿后的积累结果

利用Dechirping补偿算法得到比赛中两个目标的积累结果如图4～5。由于Keystone变换与Dechirping补偿算法已经对目标回波的距离徙动与多普勒走动进行了校正，目标回波能量聚焦效果得到明显改善，信噪比显著提升。与图1中采用常规MTD积累算法对比，可明显看出本文算法的积累聚焦优势，并且随着相参积累时间的增加，优势更加明显。由于能量聚焦更加集中，目标运动的参数估计也更加准确。对于强目标，通过积累后的结果可准确绘制出目标的跟踪轨迹。对于弱目标，其周边的杂波容易造成虚警，需要通过卡尔曼滤波进一步过滤出其跟踪轨迹。

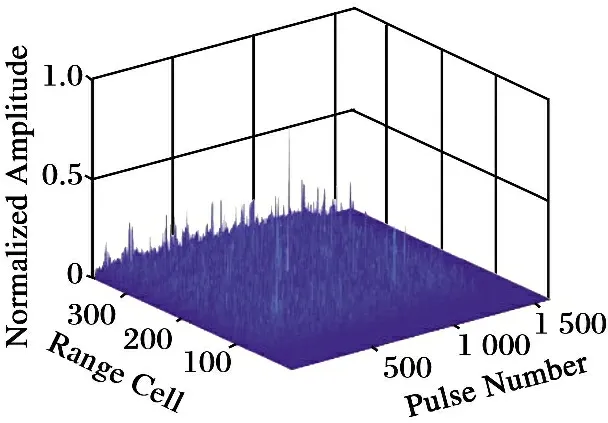
图4 弱目标的积累结果

图5 强目标的积累结果

Fig.5 The integration results of strong target

2.3 卡尔曼滤波跟踪结果

根据每帧积累结果得到可能的目标运动参数，利用基于AR模型的卡尔曼滤波进行跟踪，得到弱目标的跟踪轨迹如图 6所示。可以看出，由于杂波引起的虚警是杂乱无章的，而目标轨迹由于其运动参数的原因具有一定的规律性。因此，基于AR模型的架构能够适用于比赛场景中的机动目标探测跟踪，进一步从一片杂波分量中过滤出目标的跟踪轨迹，同时剔除了虚警。

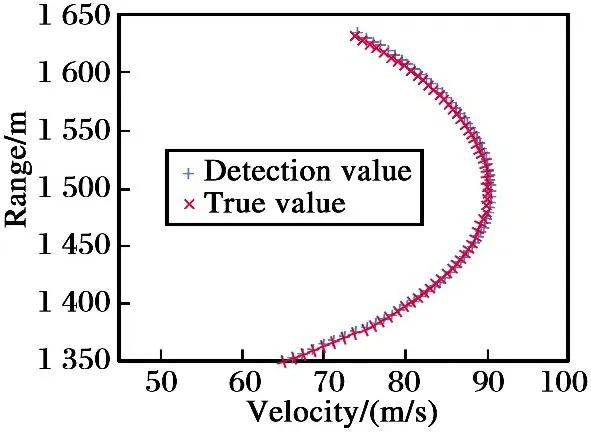
图6 目标跟踪轨迹与真值对比

Fig.6 Target tracking trajectory compared with the true value

3 结 论

Keystone变换能够在未知目标运动参数的条件下补偿目标信号包络的距离徙动。但当存在多重多普勒模糊情况下，利用Keystone变换进行目标检测的处理流程将更为复杂。

Dechirping补偿作为一种搜索补偿方法，易于实现但容易形成交叉项，对于同一距离不同运动速度的目标分辨效果较差。

基于AR模型的卡尔曼滤波通过递推过程实现状态预测和修正，数据量少、所需存储空间小，既能够处理平稳随机过程，也适用于多维和非平稳随机过程，因此可适应实际目标的复杂运动模式。

本文利用这三种算法的结合在雷达回波积累算法的运算复杂度与检测性能之间取得了平衡，所提算法简洁高效，信号处理流程环环相扣，在实际应用中可以封装成模块化进行工程实现，为新体制软件化雷达打下了研究基础。但是本文所采用的Dechirping补偿技术仅考虑到了目标运动的加速度，对于更高阶的运动目标无法进行完美的相位补偿，这是下一步需要解决的问题。希望有更好的补偿技术可以直接替换Dechirping补偿模块，快速实现算法的升级迭代。