高中数学文化教育在引言课中的实施策略初探①——以“平面解析几何引言课”为例

王克亮

(江苏省射阳中学 224300)

数学文化通常包括数学史，数学的精神、思想和方法，数学的语言，数学的应用等方面，数学文化教育应贯穿整个高中教学过程之中. 引言课通常设置在一个章节的起始，侧重回答“这个内容是什么？为什么要学习这个内容？如何学好这个内容？”等问题. 那么，如何在引言课中实施数学文化教育呢？笔者拟以近期开设的“平面解析几何引言课”这节省公开课为例，谈谈自己的一些肤浅实施策略.

1 回顾形成历史，揭示研究思想

高中数学的每一块知识内容都蕴含着一些研究思想，这些研究思想应该是教学中深植学生骨髓的东西，能对学生的终生发展起着潜移默化的作用. 那么，在引言课中如何将这些研究思想自然地揭示出来呢？笔者认为，回顾知识形成历史，沿着前人的思路行走是一个较好的策略.

在平面解析几何引言课中，笔者就是从数学史谈起的.

话题关于平面解析几何，你现在最想了解的是什么？

根据学生的回答整理成如下三个问题：(1)是什么？——平面解析几何是一门怎样的学科？(2)为何学？——为什么要学习平面解析几何？(3)怎么学？——怎样才能学好平面解析几何？

平面解析几何是一门怎样的学科呢？对这个问题的回答得从数学史谈起.在数学史上，曾经有这么几位数学家，他们雄心勃勃，想创造一种能够解决世界上一切问题的方法，法国著名数学家笛卡尔就是其中一位. 他们的设想是这样的:“任何问题→数学问题→代数问题→方程问题→求解方程→得到结论”.那么，对于几何问题，该如何用代数的方法来解决呢，这是他们遇到的难题之一.

据说，后来有一天，当笛卡尔躺在床上休闲时，忽然他看到墙角的蜘蛛网上有一只蜘蛛在爬来爬去，便突发奇想，假如在墙角的三根交线上分别标上刻度，不就能用有序的数对来表示蜘蛛的位置了吗！这正是直角坐标系的刍形. 有了直角坐标系，点就可以用数来表示，进而线与面也能用数来表示，这样用代数的方法来研究几何问题有了可能,从而使得代数与几何两者相互结合而共同发展，产生了解析几何学.

所以，解析几何学是一门用代数的方法来研究几何问题的学科. 在中学教材平面解析几何当中，将要研究直线、圆、圆锥曲线(椭圆、双曲线和抛物线)等曲线的代数表示及几何性质.

评注本节课是从发生在数学家笛卡尔身上的一个小故事开始的，自然地回顾了数学史知识，既激发了学生的听课兴趣，又揭示了本章的研究思想，能给学生留下较为深刻的印象.

2 点击核心概念，感悟数学语言

数学语言是数学思维的载体，是数学理论的基本构成成分，所以数学文化教育离不开数学语言的感悟. 那么，如何在引言课中感悟相关的数学语言呢？笔者认为，可点击一些核心概念，在逐步呈现中初步感受其数学表达.

笔者认为，曲线的方程与方程的曲线是平面解析几何中的两个核心概念，在引言课中可进行点击，并体会其数学表述.

问题1设A(4,0),B(0,2)两点确定的直线为l，如何判断点Q(-2,3)是否在直线l上？

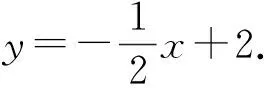
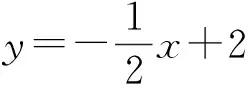
初步感受“两都”关系.

变式设A(4,0),D(4,2)两点确定的直线为m，如何判断点P(x,y)是否在直线m上？

体会该直线不是函数的图象，不能运用一次函数解析式来解决问题，并在得到关系式x-4=0后，引导学生将其改写成x+0·y-4=0.

追问1直线m与关系式x+0·y-4=0之间符合“两都”关系吗？

进一步感受“两都”关系.

体会它们都是二元一次方程，“y=f(x)”不能包含上述全部情形，自然给出“方程f(x,y)=0”这个表示形式.

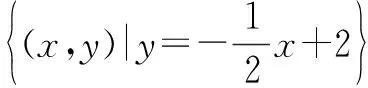
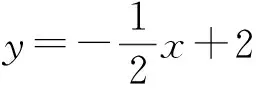
追问2“两个都”同时成立呢？

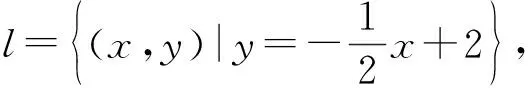
问题1.3一般地，对于曲线C与方程f(x,y)=0，当它们满足什么条件时，可称方程f(x,y)=0为曲线C的方程？曲线C为方程f(x,y)=0的曲线呢？

需同时满足“两都”关系，即(1)曲线C上任一点的坐标都是方程f(x,y)=0的解；(2)以方程f(x,y)=0的解为坐标的点都在曲线C上.

评注这里用“两都”这一数学语言贯穿前后，从点集相等的角度阐明了“数”与“形”的等价性，展现了数学语言的科学性、严谨性、简洁性和通用性.

3 力求和谐统一，展示数学之美

数学文化教育离不开数学美的熏陶，教学中如果能让学生由衷地感受到数学之美妙，对其产生的影响将是无法估量的. 那么，在引言课中该如何展示数学之美，让学生感受数学的魅力呢？笔者认为，深挖知识内涵，打通知识联系，如果能把一些内在的规律用和谐统一的形式展示出来，将会给学生强烈的震撼，美感也就会随之而来.

在平面解析几何引言课中，笔者试图将直线、圆、椭圆三者的方程用统一的形式表示出来，让学生感受到方程的美妙.

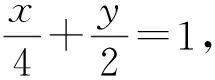
发现改写后方程的分母就是直线在两个坐标轴上的截距(可简要介绍一下截距这个概念).

利用所给截距得到三条具体直线l1,l2,l3，并推广到一般情形.

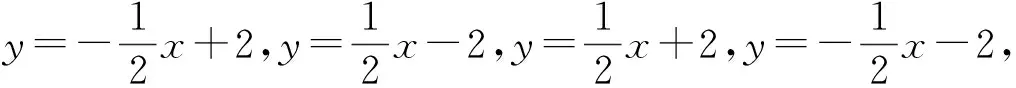
发现直线的位置关系与方程之间的联系，并体会可用方程来研究曲线的几何性质.

刚才实际上做了两件事：一是将直线转化为代数形式，得到了直线的方程；二是运用所得到的方程来研究了直线的一些几何性质.

追问解析几何的两大任务是什么？

(1)建立曲线的方程；(2)运用方程研究曲线的几何性质.

问题2以坐标原点为圆心，以r(r>0)为半径的圆O，其方程是什么样子的？

先得到关系式x2+y2=r2.

问题2.1圆O与方程x2+y2=r2之间符合“两都”关系吗？

明确x2+y2=r2就是圆O的方程.

问题2.2如何改写圆O的方程x2+y2=r2，使得它能较好反映圆O在两个坐标轴上的截距呢？

把刚才的研究结论汇总到下表内：

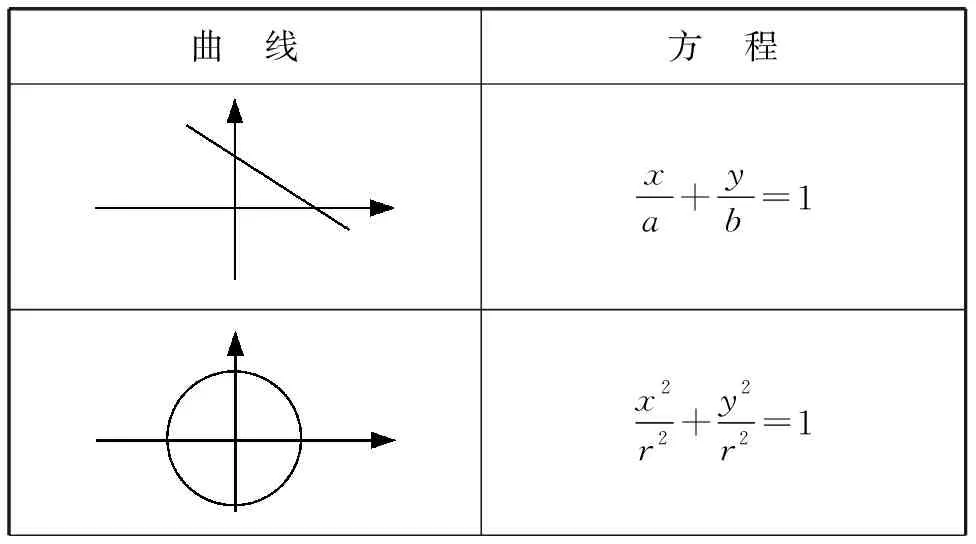
曲 线方 程xa+yb=1x2r2+y2r2=1

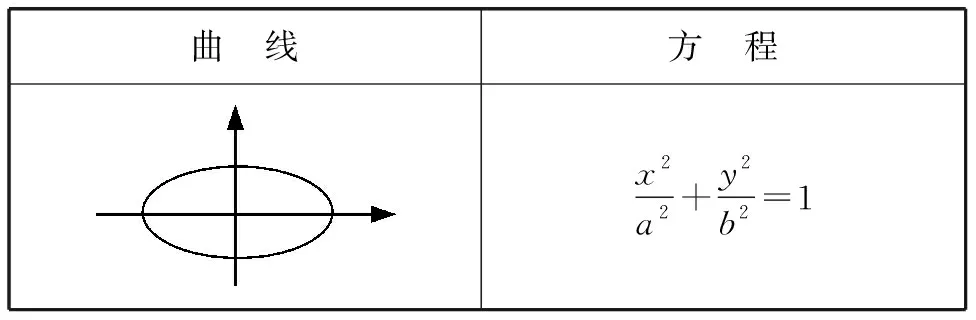
续表

从该表格中不难体会到，图形是美观的，方程是美妙的！

评注这里，当把直线、圆、椭圆的方程汇总在一张表格内的时候，相信学生会有“于枯燥之中见新奇”之感，激动与陶醉心情也会油然而生！

4 阐明学习意义，凸显知识价值

数学文化的教育还应包括介绍所学知识内容的价值，让学生消除“学了有什么用”的疑问. 那么，如何在引言课中凸显相关知识的价值呢？笔者认为，可依据知识内容的特点从多个维度阐述学习意义，特别是其在实践中的应用价值.

在平面解析几何引言课中，笔者是从“刻画效果、实践应用、理论贡献”这三个维度来展示《解析几何学》的价值的.

(1)从刻画效果看——入微

例1直线与圆的位置关系

直线与圆的位置关系相离相切相交图 形以前的判定方法d>rd=rd

解析几何的方法对图形及其位置关系的刻画，实现了细微化和精确化，即入微. 先前一些被认为是几何学中的难题，运用解析几何的方法就变得平淡无奇了.

(2)从实践应用看——广泛

现实世界中，到处有美妙的曲线，对它们的精确研究往往要借助代数方程. 比如，在建造桥梁时，首先要确定桥拱的方程，然后才能进一步设计和施工；又如，在对太空的奥秘进行探索时，要把行星的运行轨道放到笛卡尔直角坐标系中，以便精确地把握它们的运行轨迹，这样才能实现太空遨游和嫦娥登月；等等.

所以，解析几何学在实践中的应用非常广泛.

(3)从理论贡献看——巨大

对于解析几何学的诞生，拉格朗日和恩格斯这两位伟人都给予了高度评价(内容投影，此略).

因此，解析几何学的诞生，其理论贡献巨大.

总之，平面解析几何的学习，对于转变我们的数学观念、拓展我们的数学思维、提升我们的数学能力、培养我们的数学素养，都有着十分重要的意义.

评注从多个维度阐明学习的理由与意义，可充分展示知识的价值.

5 进行学法指导，聚焦核心素养

数学文化教育的目的是培养学生的学科核心素养，激发学生的学习兴趣与热情，提升学生的学习信心. 那么，如何在引言课中实现这些目标呢？笔者认为，可依据相关知识个性，立足学科核心素养的提升来给予学法指导.

在平面解析几何引言课中，笔者是站在数学建模、数学运算这两个学科核心素养的角度进行学法指导的.

(1)建立好两种数学模型

一是方程模型，这是从形到数的过程. 当遇到与图形有关的问题时，要有这样的意识，即可以通过建立直角坐标系，把图形用方程来表示，进而利用代数运算来解决问题.

二是轨迹模型，这是从数到形的过程. 一方面，当看到代数式的时候，要有这样的意识，想一下它会不会表示什么图形？有没有什么几何意义？另一方面，当看到与动点运动相关的问题时，要善于把握它的轨迹.

例2设A,B是两个定点，当动点P满足下列条件时，它的轨迹是什么图形？

(1)PA=PB；(2)∠APB=90°；(3)PA=λPB(λ>0,λ≠1)；(4)PA+PB=k(k>AB).

简析答案(此略).

在建立好两个数学模型的基础上，逐步培养一种思想，叫“数形结合”；最终形成一种观念，即“形数合一”.

(2)磨练好数学运算能力

运用代数方法来研究几何问题，离不开繁琐的运算，所以一定要在运算能力的培养上下功夫. 努力做到：消除畏繁情绪——敢算，掌握一般方法——会算，把握运算规律——善算.

评注相信学生能够从该教学片断中初步感悟到平面解析几何这门课的特点，并从中获得一些学习启示，增强学习的信心.

总之，引言课是实施数学文化教育的好时机，能较好培养学生的学科素养.