含风电场的电力系统无功优化研究

摘要：随着风力发电渗透率的逐渐提高，风机出力的随机性给电力系统带来更多不确定性因素。采用电压稳定裕度确定系统电压临界崩溃点并在此处接入风机，利用双馈风机能够发出无功功率的特点稳定系统电压。根据风速变化曲线，将风速划分为5个典型风速段，建立以有功网损最小和电压偏移最小为目标的无功优化数学模型，采用改进粒子群优化算法进行求解，应用IEEE 30节点系统进行测试，验证所提算法的有效性和可行性。

关键词：风电场;电力系统;无功优化;电压稳定裕度;粒子群算法

中图分类号：TM614;TM714     文献标识码：A    文章编号：1674-1161（2019）06-0026-06

随着风力发电技术的日益成熟，风力发电并网已成为改善能源结构、减轻环境污染的发展趋势。但由于风力发电出力具有随机性和间歇性的特点，其接入位置会改变电网的无功分布，进而影响系统电压水平及电压稳定性。目前大多数文献研究的重点放在风机的场景划分和无功优化模型建立及求解方法上，而没有规划风机安装的位置。根据风速变化曲线，将风速进行分段，把动态无功优化转为多个风速段的静态无功优化，进而建立以有功网损最小和电压偏移最小为目标的含风电场的电力系统无功优化模型，再使用改进粒子群优化算法对IEEE30节点测试系统进行无功优化仿真计算。

1 双馈风机功率输出确定

目前双馈感应式风机是风电场中的主流机型，其风能转换为机械能的过程遵循贝兹定理，因此，双馈风机从风能中获得的机械功率为：

PM=0.5ρπR2Cp（β，λ）v3                  （1）

其中：ρ为空气密度kg/m3;R为风力机叶片的半径，m;Cp（β，λ）为风能利用系数，是关于桨距角β和叶尖速比λ的函数，λ=;ω 为风力机的机械角速度;v为风速。由贝兹定理可知， Cp（β，λ）≤0.593，当叶尖速比大于3时，其能达到最大值。在工程应用中， Cp （β，λ）一般由风机制造商提供。

設双馈风机功率因数恒定，则风电机组的无功出力为：

Qw=Pw·cosφ         （2）

式中：cosφ为风电机组的功率因数。

2 无功优化数学模型

2.1 目标函数

以有功网损最小为目标函数，节点电压和发电机无功出力约束以罚函数的形式加到目标函数中，即：

minf=minPloss=gij（U2i+U2j-2UiUjcosθij）+

λ1

+λ2

（3）

式中：NB，NPQ，NPV分别为所有支路集合、PQ节点集合和发电机PV节点集合;λ1，λ2分别为节点电压、无功越界的惩罚因子;gij，θij分别为节点i， j之间的电导和电压相角差;Ui，Uimax-Uimin分别为节点i的电压幅值及其上下限值;Qi，QGi，max，QGi，min分别为发电机节点i的无功出力及其上下限。 Uilim，QGi，lim分别表示对应变量越限时的设定值，定义如下：

2.2 约束条件

约束条件包括等式约束和不等式约束。

1） 等式约束。等式约束为有功、无功的潮流平衡方程。

式中：Pi和Qi分别为节点i处注入的有功功率和无功功率;Gij和Bij分别为节点i，j之间的电导和电纳。

2） 不等式约束。不等式约束包括控制变量和状态变量约束。控制变量不等式约束为：

式中：NG、NC、NT分别为系统发电机节点数、无功补偿节点数、可调变压器数;UGi为发电机节点电压值;QCi为节点i的无功补偿量;TK为可调变压器的变比：UGi，min，UGi，max， QCi，min，QC，max，TK，min，TK，max分别为相应变量的上、下限值。

状态变量的不等式约束为：

式中：Ui为节点i的电压幅值;UGi为发电机节点无功出力;Ui，min，Ui，max，QCi，min，QCi，max分别为相应变量的上、下限值。

3 风机的位置确定

通过求解电压稳定裕度方法确定风机安装位置。在功率因数确定的情况下，将风机当作PQ节点来进行运算。由于双馈风机不仅发出有功，还发出一定的无功功率，故可通过求解电压稳定裕度将风机放在电压较差的位置，来改善系统的电压。

以单线路2节点系统为例，如图1所示。

设U&i=Ui<0 °，图1中2节点电路的支路电压方程为：

支路末端节点输出的功率为：

在式（10）、（11）、（13）、（14）中消去电流分量后，可获得

式中：支路导纳为G+jB，通常输电线路中电纳为负值，因此取Gij=G， Bij=-B， 则以电压分量为变量的式（15），（16）的圆的标准形式为：

式 （17 ）表示的圆 UP 的圆心为 OP ，其半径为 rP ，式（18）表示的圆 UQ 的圆心为OQ，其半径为rQ。两圆的圆心OP，OQ 的坐标分别为：

两圆圆心之间的距离为：

式（17）、（18）只有当两圆半径不小于零且两圆相交或相切时存在解。

图2和3分别为两圆相交和相切的情况。当两圆外切时负荷电压处于临界崩溃，为避免这种情况发生，可以增加负荷的有功功率和无功功率。图3中两圆相切对应的运行点P1为临界电压崩溃点。需满足rP≥0;rQ≥0;rP+rQ≥D。在潮流计算每次迭代过程中检验各支路是否满足条件。如果不满足条件，则该支路末端节点电压达到临界，该节点即为系统无功缺额最大的节点，即风机接入位置。

对系统进行电压稳定裕度计算，结果如表1所示。

由上述数据可得27节点所在支路的电压稳定裕度最低，即电压最容易面临崩溃，故选节点27作为双馈风机接入位置。

根据式（1）计算，得到FLl500型风力发电机功率输出，并与工业参数对比（见表2）。按此模型计算FLl500型1.5 MW风力发电机在不同风速下的有功功率输出，其额定风速为11 m/s左右，即在此风速下以额定功率1.5 MW输出。图4是该类型风力发电机输出功率的实际曲线和计算曲线。

从图4中可以看出，在风速小于13 m/s这段范围内，风力发电机输出功率的实际曲线和理论计算曲线相差很小。在实际工程应用时，当风速超过额定风速12 m/s后，风力发电机将通過齿轮箱等装置调速，既保护风力发电机，又稳定了输出功率。可见，只有在小于或稍微大于额定风速的情况下，贝兹模型才是合理的。

关于含风电场电力系统多目标无功优化算法流程，无功优化的求解采用改进粒子群优化算法，仅需将粒子群优化算法的潮流计算过程加入风电场的有功无功处理即可，其余过程保持不变。

4 算例仿真

采用IEEE30节点标准系统来进行验证。该系统共有30个节点，6个发电机节点为1，2，5，8，11，13，节点1为平衡节点，其余5个节点为PV节点，除发电机节点外其他均为PQ节点。控制变量共12维，包括6个发电机节点电压、4个变压器变比和2个可投切并联电容器组。4个变压器支路分别为6-9、6-10，4-12，27-28，分别用T1，T2，T3，T4表示，在10，24节点装有并联电容器组。发电机节点电压上限和下限分别为1.1和0.9，PQ节点电压上限和下限分别为1.05和0.95，变压器变比的上限和下限分别为1.1和0.9，共9个档位，每档为0.025，电容器10节点和24节点补偿容量上限分别为50 MVA和10 MW、下限均为0 MW，其中10节点分5组，每组容量为10 MW，24节点分5组，每组容量为2 MW。系统基准容量为100 MW。

初始条件下，设置发电机的机端电压和可调变压器的变比均为1.0 p.u.，补偿电容器容量为0 MW时，通过潮流计算，初始网络损耗为8.421 MW。

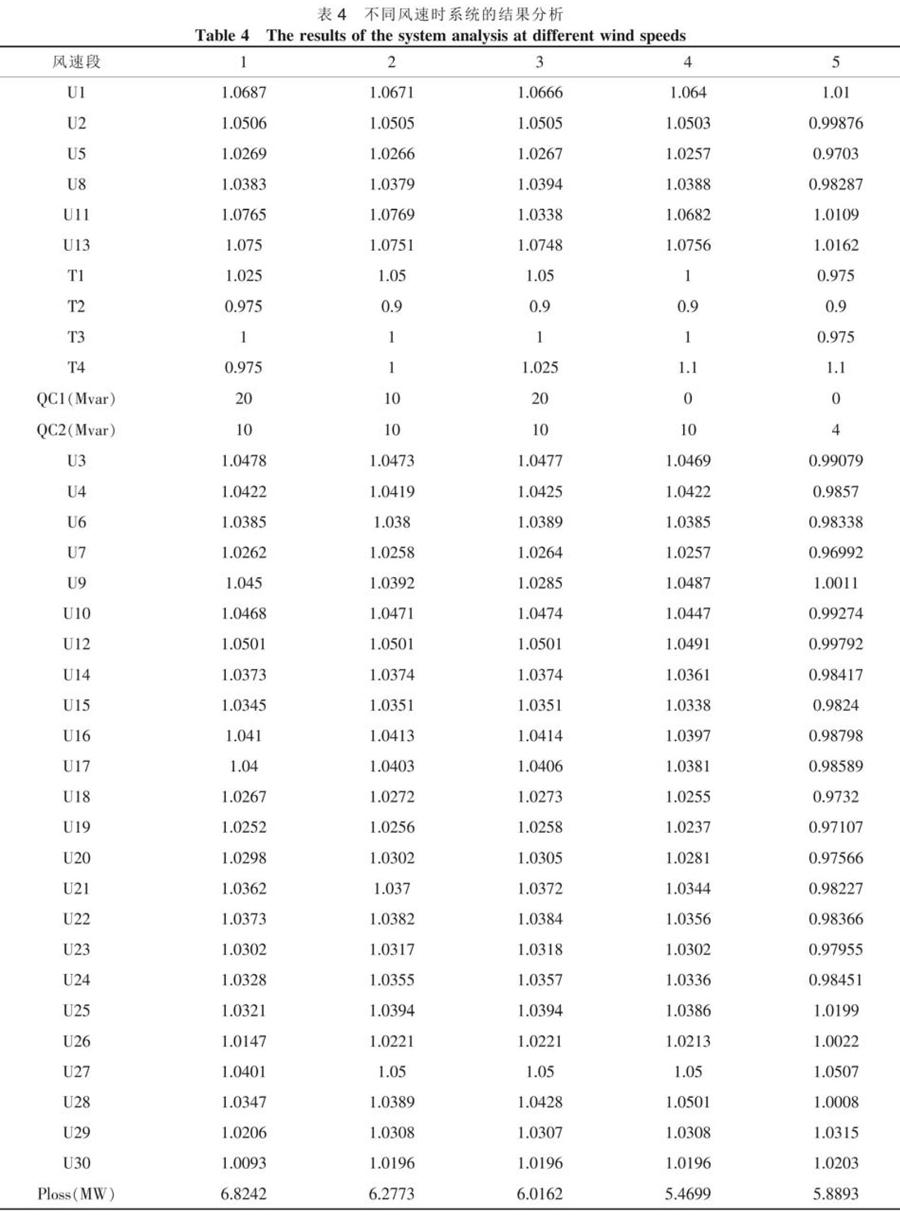
在27节点有一个风电场，总功率出力45 MW。该风电场含30台风机，单台风机1.5 MW，含风电场无功优化采用分段考虑，将风速化分为5个典型风速段，功率因数取恒定值cosφ=0.7，参数见表3。取每一风速段进行仿真，运行10次，取最小值。不同风速时系统结果分析见表4。

从表4可以看出，随着风机出力的增加，系统有功网损趋于减小，同时缓解电网的输电压力。这是因为大型风电场接入系统后可为当地负荷提供一定的有功出力，减少了系统中的有功流动。而当风机并网后输出功率过大时（风速段5），会对系统产生负影响，故风机并网应考虑风机接入容量大小。

5 结论

采用电压稳定裕度方法确定系统电压薄弱点，利用双馈风机可发出无功功率的特点，在系统电压临界崩溃点接入风机，以维持系统电压稳定。此外，针对风速的波动性和间歇性，采用分段优化的方式进行无功优化，对风电机组输出功率的随机变化具有较好的适应性。大容量风电接入系统可有效减小系统网损，减少常规机组有功出力，缓解电网输电压力，在实际应用中结合负荷及风速预测信息可实现在线优化。

收稿日期：2019-07-26

作者简介：刘晓宇（1972—），女，高级工程师，从事电网运行工作。

参考文献

[1] 范李平， 杨力森， 武粉桃. 风电场并网对电力系统稳定性影响[J].电网与清洁能源，2009，25（6）：58-61.

[2] 姜凤利，朴在林，吴  硕等.分布式发电对农村配电网电压分布和网损的影响[J].沈阳农业大学学报，2014，45（2）： 200-204.

[3] 陈海焱，陈金富，段献忠.含风电机组的配网无功优化[J].中国电机工程学报，2008，28（7）：40-45.

[4] 何禹清，彭建春，毛丽林，等.含多个风电机组的配电网无功优化[J].电力系统自动化，2010，34（19）： 37-41.

[5] 徐基光. 自适应网格密度改进粒子群算法在多目标无功优化中的应用[J]. 电网与清洁能源，2017，33（2）： 21-25.

[6] 姜凤利，张宇，王慧.基于引导策略自适应粒子群算法的农村电网无功优化[J].沈阳农业大学学报， 2017，48（1）：122-128.

Reactive Power Optimization in Distribution System with Wind Farm

LIU Xiaoyu

（Stategrid Liaoning Dandong power supply company， Liaoning Dandong 118000， China）

Abstract： With the gradual increase of wind power penetration rate， the randomness of wind power output brought more uncertainty factors to the power system. The voltage stability margin was used to determine the critical voltage collapse of the system. And the wind turbines were accessed at the node. Then the system voltage could be stabilized with the characteristics that the double-fed induction generators can output reactive power. According to the wind speed variation curve， the wind speed was divided into five typical wind speed sections. With the target of minimum loss of the active network and minimum system voltage deviation， the reactive power optimization mathematical model was established. An improved particle swarm optimization algorithm was adapted to solve the problem.The IEEE 30-node system was used to test the validity and feasibility of the proposed method.

Key words：wind farm， power system， reactive power optimization，voltage stability margin， particle swarm optimization