“让学促思”

柯仁美　郑为勤

摘 要：在初中数学教学过程中，把学习的主动权交还给学生，这就是“让学”，在学生学习的道路上，教师需要不断引领与点拨，这就是“促思”。“让学促思”的实质就是生本化的启发式教学，有别于传统意义上的启发式教学与片面强调的以生为本，“让学促思”使思维课堂得以展开，使有效教学得以实现，使核心素养的培养更容易达成，其途径有：立足基础，“让学”使“促思”更投入;拓展思维，“促思”使“让学”更深入;培养习惯，“促思”使“让学”更轻松。

关键词：初中数学;让学促思;生本化

笔者参加工作几十年，所经历的课改潮已经有好几轮了。刚参加工作时，启发式教学红遍大江南北;新世纪，新课程与生本化理念随之而来;几年前，思维课堂、有效教学一度成为网络热词。最近，核心素养与“让学引思”又在很多地方搞得轰轰烈烈。而且各地涌现了许多五花八门的教改经验，不管如何名词翻新，教学的对象是学生，“以学生为中心”是各派的共识，以启发式教学替代陈旧的灌输式教学是必须的。

海德格尔说，“教，要的就是‘让学！”作为教师，要把学习的主动权交还给学生，这就是“让学”，在学生学习的道路上，教师需要不断引领与点拨，这就是“促思”。“让学”是“促思”的前提，“促思”是“让学”的归宿。结合自己的学习与实践，以下谈谈如何在初中数学教学中实施“让学促思”策略，以达到数学课堂的生本化，实现有效教学。

一、 立足基础，“让学”使“促思”更能投入

“让学”，就是给学生在课堂上创设充足的时空去投入阅读、思考、操作与交流讨论。课堂研究与交流应充分尊重学生的现有基础，根据全班学生的普遍学情与不同学生的不同基础来设计“让学”的过程。

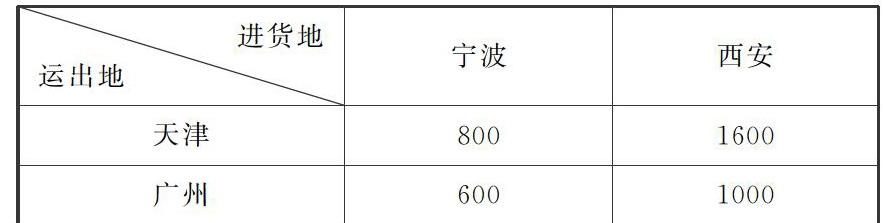
例如，有这样一道应用题：天津与广州都有某种精密仪器可提供外地使用，其中天津可以提供10台，广州可提供4台，已知有宁波与西安两个城市需要这些仪器分别是6台与8台。每台仪器的运费（元）如下表所示，有关部门打算用15200元运送这些设备，请你设计一种方案，使宁波与西安都能得到所需设备且费用正好符合规划。

这是学生学习了一元一次方程后的一道方案设计型的应用题，此时大部分学生已经能够解答较复杂的一元一次方程，但缺少根据题目意思有顺序思考并用含x的一次式来表示相关数据的意识与能力。笔者认为在一开始的“让学”环节可以让学生去碰碰壁，体验一把无所适从的“失落感”。当学生百思不得其解之时，巧妙的“促思”会让学生有如获至宝的感觉：可以设定其中一条线路的运输台数为x，然后把别的线路的台数用包含x的一次式表示出来。当学生会用一种解法时，教师可以让学生变换设x的位置，从而起到融会贯通的作用。

在传统教学过程中，教师往往直接给学生一把钥匙，指定他们用这把钥匙去开特定的门。学生就像一个刚刚吃过饭的小朋友在还没有饿的情况下被父母逼着吃面包，久而久之，即使是最好的食粮，对他们来说都是一种负担。自从启发式教学被提及以后，不少教师就是背离了学生的需求，进行单方面的启发，最终往往是启而不发。所以说，要充分了解学生的学习基础，更要让学生自己去经历学习过程，只有足够充分的让学才能使学生感受到解题的艰辛，也才能最大限度激发学生对“促思”的珍惜。

二、 拓展思维，“促思”使“让学”更加深入

“让学促思”必须基于课堂思维的不断拓展，引导学生由浅入深，由知识到技能进行探究。如在教学二次根式这块知识，当学生已经初步知道二次根式的概念后，教师可以出示以下探究题：

（4）（a）2与a2分别表示什么意思，他们是否相等，他们的区别与联系是什么？

这里的四个探究题可以放手让学生进行分组讨论交流，学生在组内合作交流，然后班级集中请各小组派代表交流观点。学生分组讨论的时候，教师应加强巡视，发现学生的一些特殊想法，以便更好地了解学情，最后在教师的引导下让学生总结出相应规律。传统的教学中，教师往往在学生简单作答后就得出规律，看似节约了时间，实则是“让学”足，“促思”不够。今后当综合性强的习题出来的时候，学生就会不知所措，到那时再来补课就是马后炮了。可见，合理做好新概念的拓展促思工作有事半功倍之效。

三、 围绕学法，“促思”使“让学”更见效益

传统教学中的启发式教学往往非常重视启发的形式，容易忽视启发的内容，甚至出现背离教学目标的现象。众所周知，新课程将学会学习作为三维目标的第二大目标，过去我们只是引导学生去解某道题，以成功解答为目标的教学，其落脚点在会做当前某道题上，难免会忽视思维能力与思维方法的培养，最终难以达到会做同类题的结果。所以，课堂教学的“促思”应该以学法指导为重点，在初中数学教学中，数学思想的渗透与指导显尤为重要。

比如对于分类讨论思想，过去我们往往跟学生说，像这样的题目需要分类讨论，学生听后明白了是这道题目需要分类讨论，但不知道为何这道题目需要分类讨论、怎么开展分类讨论。难怪有的学生经常问老师：老师，这道题需要分类讨论吗？出现这种现象的原因就是教师对分类讨论的情况有什么条件没有指导到位，没有充分让学，导致学生被动思考、简单作答所致。如这有一道探究题，如图：假如沿直角三角形的斜边中点向两直角边方向剪两刀，剪去两个三角形，剩下的图形是如图所示的直角梯形，请问原直角三角形的斜边长是多少？

假如只是简单地“让学”，大部分学生往往只找到一种可能性，即使有别的同学影响下使他们知道这里应该分类讨论，他们也只不过是接受了一个答案而已。此时，科学的引思特别重要。教师可以问：大家想一想，拿到这道题，我们是不是只要马上去补充画出一个符合条件的直角三角形，然后求斜边的长呢？这里的条件能够保证我们精确地画出一种特定的情形吗？经过思考与观察，学生发现题目所示的直角梯形有两个直角，而原来只有一个直角，而哪个是原来的直角呢？此时就会出现两种情况，要么画右边那个角是直角，要么画左边那个角是直角，然后才可以进一步深入探讨不同情况下斜边的长度。那样学生就知道了，由于图画所指示的具体情形存在不确定性，导致了补充图画会有两种可能，而这两种可能的分类标准是原直角的位置。为了深化学生对直角三角形条件下的分类思想，可以再出两个比较性的问题：（1）已知一个直角三角形的斜边长为43，一直角边长为33，求另一条直角边的长度。（2）已知一个直角三角形有两边长分别为43与33，求另外一条边的长度。让学生再次说说什么情况下需要分类，分类遵循的标准是什么，这样学生就能慢慢习得应该拥有的数学思想。可见，科学引思才能真正使学生在“让学”中学到真本领，“引思”的深度决定了“让学”的有效度，“引思”的方向影响“让学”目标的达成度。

四、 培养习惯，“促思”使“让学”更为轻松

“教是为了不教”，随着知识的熟练，人的思维操作也逐渐成为一种习惯。课堂“促思”的目的是为了把生硬的行为熟练化、习惯化，最终能轻松驾驭不同的问题情境。

比如，有一次，在教学一道逻辑推理题的时候，很多学生一边画图一边绞尽脑汁，百思不得其解。这时，笔者就给学讲了一个故事：有一次毛主席让警卫员小赵把办公室的沙发搬出去，小赵抱怨说：“主席，这门这么小，沙发这么大，我们就是搬不出去啊，看来是找不到办法了。”毛主席說：“小赵同志，你说这个沙发是在造房子之间就留在房间里的吗？”听了主席的话，小赵终于恍然大悟：怎么把沙发搬进来的，就用什么方法把沙发搬出去，只要有办法搬进来，就有办法把沙发搬出去。借用这个故事，学生明白了：搬沙发出去的方法，就是要用搬进来的方法才行。这样他们就悟到逆向思维的重要性。之后，学生也渐渐养成“此路不通，换个思路”“正走不行，倒走试试”的解题习惯，也有了“办法总比困难多的”的意识。

“让学”与“促思”是同一教学过程两个不可或缺的方面，两者相辅相成，合成教学的一体。过去我们在提及教学理念的时候，往往会片面着重一方，而忽视甚至丢弃了另一方，导致教学改革裹足不前。其实“让学促思”的实质就是生本化的启发式教学，有别于传统意义上的启发式教学与片面强调的以生为本，“让学促思”使思维课堂得以展开，使有效教学得以实现，使核心素养的培养更容易达成。

参考文献：

[1]华云锋.“让学引思”：初中数学课堂的新视点[J].教学与管理，2017（4）.

[2]陈荣春.“三学”课堂：以“让学引思”为内核的深度学习变革[J].江苏教育研究，2017（1）.

[3]勾余波.初中数学教学中以惑为诱教学方法的应用分析[J].科学咨询（教育科研），2018（4）.

[4]付东丽.初中数学教学方法初探[J].教育教学论坛，2010（1）.

[5]武晓鹏.浅谈初中数学教学中的问题教学方法[J].学周刊，2019（2）.

作者简介：

柯仁美，郑为勤，福建省三明市，福建省三明市大田县第六中学。