基于不同回收主体下闭环供应链收益协调研究
杜志平 付帅帅 王丹丹 李亭亭


中图分类号:F224 文献标识码:A
内容摘要:本文针对废旧电子产品回收问题,建立含有单个制造商和两个零售商的闭环供应链系统,分别探讨在零售商、制造商分别主导回收这两种回收模式下,零售商进行分散与集中决策时,供应链上各节点成员与供应链整体的收益协调问题,并通过算例分析对供应链内不同主体主导回收模式下的收益协调问题进行探讨。结果证明:在不同回收模式下,废旧电子产品市场容量的高低对供应链各节点成员的收益具有不同影响;而在零售商进行分散决策时,供应链整体的收益会随着废旧电子产品市场容量的增加而显著增加。
关键词:闭环供应链 回收模式 收益协调 博弈论
随着电子产品更新速度的加快,产生大量废弃电子产品使生态治理面临巨大挑战。随着国家对社会可持续发展与绿色发展以及循环经济发展的要求不断提高,防止资源浪费与改善环境等问题变得刻不容缓,而废旧电子产品作为循环回收利用材料,具有较高的资源价值,建立高效的回收体系也是我国发展生态文明的需要,为此,针对废旧电子产品的闭环供应链管理也成为学术界及企业界研究的热点。国内外学者分别从不同角度对闭环供应链回收模式及收益协调方面进行了研究,如Svaskan等提出了包括制造商、零售商、第三方回收的闭环供应链模型。Hong等在Svaskan研究的基础上,对闭环供应链中不同的第三方企业对废旧电子产品回收与处理进行了对比分析。Atasu等从回收成本的角度对闭环供应链的回收渠道进行了探讨。倪明等构建了三种双渠道闭环供应链回收模式,并通过模型求解证明了这几种回收模式下的闭环供应链均有增加。在闭环供应链收益协调方面,高文军利用博弈模型设计出闭环供应链协调的收益共享及费用共担契约,并指出协调契约可保证闭环供应链各方共同收益。
综上所述,上述学者对于闭环供应链的研究丰富了其优化理论,也具有一定的借鉴意义,但其对于闭环供应链都是从单一视角进行研究,未能从系统分析其回收渠道与收益协调之间的关系,且研究主体主要是针对单一制造商与零售商回收的闭环供应链。为此本文通过建立含单个制造商与两个零售商的闭环供应链,对供应链内不同主体主导回收模式,及现实中零售商因各种因素致使回收价格的不同,对供应链各节点成员与供应链整体的收益协调问题进行探讨,并分析其与废旧电子产品市场容量的关系,并利用算例对上述分析进行证明,以期为相关参与者提供决策支持。
问题描述及假设
图1中的模型包含单个制造商及两个竞争性的零售商,当零售商作为回收主体时,其负责新产品的销售工作及废旧电子产品的全部回收工作,以一定的价格批发给制造商;而制造商作为回收主体时,其负责新产品的生产再加工销售工作、废旧电子產品的再处理工作,以及全权负责废旧电子产品的回收工作。其中M代表制造商,RA和RB代表链上的两个竞争性零售商,∏M代表制造商的收益函数,∏A和∏B分别代表零售商A和零售商B的收益函数,闭环供应链的总收益为:Π=ΠM+ΠRA+ΠRB。cm表示制造商生产初次新产品的单位生产成本,cr代表制造商生产再造品的单位生产成本,则θ=cm-cr,θ表示制造商因回收废旧电子产品进行生产再造品而节约的单位生产成本。新产品市场需求的函数是:Di=Di(P1,Pj)=Q-αPi+βPj,i≠j且i,j=1,2。Q表示市场总需求量,α、β分别表示消费者对零售商A和B的市场价格P1和P2的市场敏感系数,且根据市场规律可知α>β>0。令Di=Di(Pi,Pj)=N+Pi-εPj,i≠j且i,j=3,4,代表废旧电子产品的回收量,当N越大时则消费者的社会环保意识越强。、ε均为常量,表示消费者对零售商A与零售商B的两种废旧电子产品的回收价格P3与P4的敏感系数,且由市场规律知:ε>>0。
模型假设为:制造商的初次新产品和回收再造品是同质的,再造品对消费者购买偏好影响不大,所有节点成员的决策过程为完全理性。两种不同回收模式下,制造商M与零售商A、B之间信息始终完全对称,而零售商分散决策时彼此信息不对称,集中决策时信息完全对称,此时零售商A、B通过联盟得到最佳收益,并进行平均分配。各节点企业全部为风险中性,但决策时坚持个体理性,即节点企业在决策时出发点是实现自身收益的最大化。
不同回收主体下的决策模型分析
(一)零售商主导回收模式
零售商分散决策。当零售商作为回收主体时,零售商A、B各自决定其销售价格以及所负责回收的废旧电子产品的市场回收价格。制造商给零售商A、B的批发价格为W,零售商A、B批发产品的市场售价分别为P1、P2,零售商A、B的固定回收成本分别为C1、C2。零售商A、B的市场回收价格分别为P3、P4;制造商M从零售商A与零售商B处回收的废旧电子产品的回收价格为W0。当零售商采取分散决策时:制造商M、零售商A、B的收益函数可分别为:
∏M=(W-cm)(D1+D2)+(θ-W0)(D3+D4),∏RA=(P1-W)D1+(W0-P3)D3-C1,∏RB=(P2-W)D2+(W0-P4)D4-C2
利用逆向归纳法,求得制造商M、零售商A、B的最佳收益分别为:
综合可得到整条供应链的收益:
零售商集中决策。零售商A、B集中决策时,双方共同决定市场零售价格P及电子产品回收价格P0,并共同承担废旧电子产品回收固定成本C,令C1>C/2,C2>C/2。此时制造商M会根据零售商制定的市场零售价P来确定产品的市场批发价W以及废旧品回收价W0,新产品市场需求函数为:D(P)=Q-αP+βP,废旧电子产品的市场回收总量为:D0=(P0)=N+γP0-εP0。零售商A、B集中决策时,则∏R=∏RA+∏RB=2(P-W)( Q-αP+βP)+2(W0-P0)( N+γP0-εP0)-C,制造商收益函数为:
∏M=(W-cm)D(P)+(θ-W0)D0(P0)=(W-cm)(Q-αP+βP)+(θ-W0)(N+γP0-εP0)
同理得制造商M和零售商A、B的收益分别为:
结果分析。对制造商M在零售商分散决策和集中决策下的收益进行求差运算得:
对零售商A、B在其集中决策与分散决策下的最佳收益进行求差,即:
由上述结果知:在零售商主导回收时,制造商M在零售商集中决策时的收益小于零售商分散决策时的收益,表明零售商进行联盟决策时会减少制造商的最终收益。当零售商集中决策得到的收益大于其分散决策时的收益时,证明在零售商进行主导回收模式下,各零售商可通过共同实施联盟决策,以获得更大收益。
(二)制造商主导回收模式
在制造商进行主导回收模式下,设定制造商承担回收的固定成本为C,废旧产品的回收价为P0,其余相关变量均与上述相同。
零售商分散决策。零售商A、B进行分散决策时,可视为非完全信息对称,此时各零售商卖出的电子产品市场售价分别为P1和P2,此时制造商、零售商A、B的需求函数分别为D0=N+ξW0、D1=Q-αP1+βP2、D2= Q-αP2+βP1。此时三者的收益函数分别为∏M=(W-cm)(D1+D2)+ (θ-W0)D0-C、∏RA=(P1-W)D1、∏RB=(P2-W)D2。
同理求得制造商与零售商A、B的最佳收益分别为:
闭环供应链的整体收益为:
零售商集中决策。零售商A、B进行集中决策时,双方需求函数及收益相同,即零售商先共同决定二者联盟时的市场售价P,且共同承担回收时的固定成本C。制造商会根据零售商联盟决定的市场售价P动态调整给零售商的市场批发价W及废旧电子产品的回收价格W0。此时制造商、零售商的需求函数分别为D0=N+ξW0、D(P)=Q-αP+βP。制造商、零售商的收益函数分别为:
∏M=(W-cm)D(P)+ (θ-W0)D0(W0)-C,∏RA=∏RB=(P-W)D(P)
求得制造商与零售商A、B的最佳收益分别为:
此时闭环供应链的整体收益为:
结果分析。对制造商M在零售商分散决策和集中决策下的收益进行求差运算得:
结果表明,当制造商主导回收废旧电子产品时,制造商M在零售商分散决策下所得的收益大于零售商集中决策下的收益,说明零售商进行联盟决策会影响制造商的最终收益。
对零售商A、B在其集中决策与分散决策下的最佳收益进行求差,即:
由求差结果知,当制造商主导回收废旧电子产品时,零售商A、B在集中决策下的收益大于其在分散决策下的收益。结合上述分析結果可知:不论在制造商主导回收,还是在零售商主导回收废旧电子产品,零售商进行集中决策可使自身利益最大化。
算例分析
以某电子生产制造加工厂为例,消费者对新产品市场价格的敏感系数为:α=50,β=2,对市场回收再造品的市场价格的敏感系数为:ξ=100,ε=10,=1,制造商利用初次新材料的加工成本cm=30,利用回收的废旧电子品零部件的成本为:cr=10,那么θ=cm-cr=20。假设废旧电子产品总市场容量N=100时其市场回收价为0;当零售商分散决策时,零售商A、B的固定回收成本是:C1=80,C2=70,当零售商集中决策时,零售商A、B的固定回收成本都为C=30。
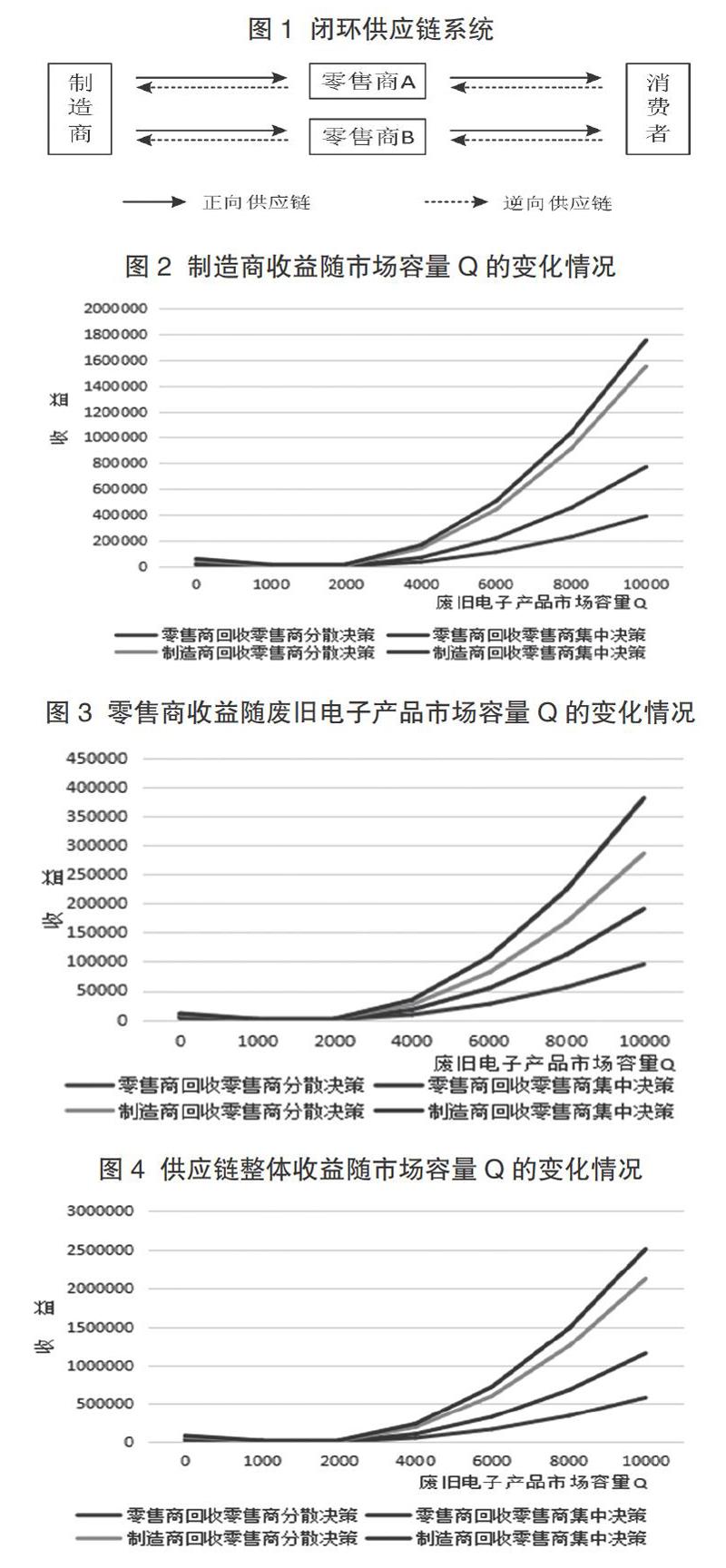
(一)制造商收益随市场容量的变化情况
由图2可知,无论零售商如何决策,制造商收益∏M在两种回收模式下都随废旧电子产品市场容量Q的增加而不断增加,当Q大于4000后,制造商的收益随Q的增加而显著增加。可知若制造商要获得更多收益,在不考虑其他固定成本的情况下,可选择零售商A、B集中决策,同时由其主导回收废旧电子产品。
(二)零售商收益随市场容量的变化情况
由图3可知,无论零售商如何决策,其收益∏Ri在两种回收模式下都随着市场容量Q的增加而不断增加,当Q大于2000时,零售商收益在制造商主导回收且零售商进行集中决策时,增加的幅度较其他三种方式更大。因此零售商若要获得较大的市场收益,可以选择制造商主导回收废旧电子产品模式,且进行集中决策,这也证明供应链节点企业进行合作的重要性。
(三)供应链整体收益随市场容量的变化情况
由图4可知,供应链总体市场收益∏在以上四种回收方式下均随着市场容量Q的增加而增加,且其在制造商负责回收,零售商进行集中决策时收益增加的更为显著。因此若追求供应链总体收益最大化,可选择由制造商主导回收,零售商集中决策的回收模式。
由上述分析可知:当市场容量一定时,制造商收益在零售商分散决策下取得较大值,且当制造商负责回收时可取得最大收益。零售商收益在集中决策时可取得较大值,说明合作博弈对零售商最终收益具有积极影响,同时零售商作为回收主体时比制造商作为回收主体的收益更加显著,随着市场容量Q增加,优势更加突出。供应链整体收益与废旧产品市场容量Q直接相关,在零售商主导回收模式下,Q小于某一定值时,供应链整体选择零售商集中决策时可取得较大收益;当市场容量小于该定值时,整体收益在零售商分散决策时取得较大值。而当制造商主导回收时,供应链整体收益在零售商两种不同决策行为下的优劣情况极为相似。同时通过数据整理分析发现:供应链整体收益在两种不同的回收模式下,零售商进行分散决策时,收益值会随着市场容量的增加而显著增加。
参考文献:
1.倪明,张族华,郭军华,杨善林.不确定需求条件下双渠道回收闭环供应链回收模式比较[J].系统工程,2017,35(2)
2.高文军.双因素影响回收下的闭环供应链协调契约设计[J].中国流通经济,2014(3)
——博弈论

