一类Wick-型随机Gardner方程的精确解

吴大山，孙峪怀，杜玲禧

（四川师范大学数学科学学院,四川成都610066）

目前对于非线性偏微分方程的精确解的研究在学界已经形成了一系列行之有效的方法,如tan函数展开法[1-2]、F-展开法[3].但是在实际应用之中更多的是随机现象, 所以在随机环境之下研究随机偏微分方程的精确解意义重大.荷兰数学家Kotreweg和他的学生De Vries 在1895 年研究浅水波运动时, 建立了著名的浅水波方程并使用直接积分法求出浅水波方程[4-6]的孤立波解.浅水波一般形式为：

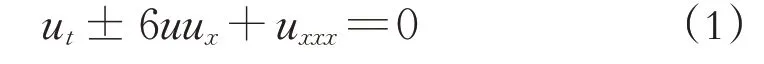
方程（1）称为Kotreweg-DeVries（KdV）方程.1967年Gardner通过逆散射方法[7-9]求出了KdV方程的孤立波解.对于Gardner方程,其一般形式如下：

其中a(t),b(t),d(t),f(t),h(t)是关于时间t的函数.文献[10-12]也给出了Gardner方程的各种精确解.

文献[13]给出了一类随机KdV方程

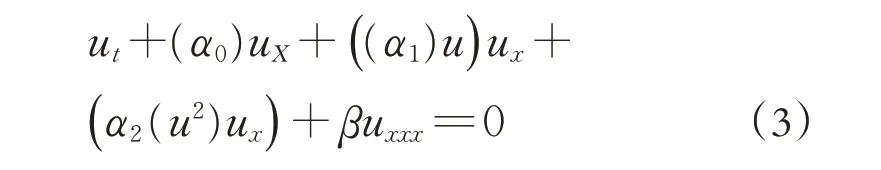
在Kondratiev 分布空间S(-1)上的Wick 乘积对应的Wick-型随机KdV方程

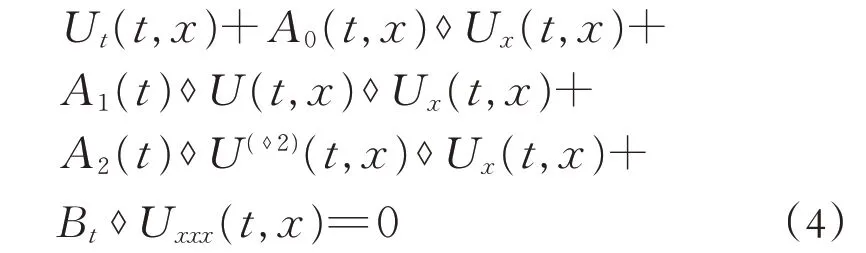
的精确解. Waditi 通过反散射方法求出非线性随机KdV 方程的精确解, 并建立了带随机扰动偏微分方程的理论基础. Holden 引入了白噪声分析方法, 提出了Wick 型随机偏微分方程[14-15], 在此基础之上,Chen和Kim分别研究了随机Kadomtsev-Petviashvili（MKP）方程和变系数广义随机Boussinesq方程.

本文运用Hermit变换和函数展开法[16-17]研究方程（2）在Kondratiev 分布空间S(-1)上的Wick 乘积之下对应的Wick-型随机Gardner方程

的精确解. 式中⋄是Kondratiev 分布空间上的Wick乘积, 是定义在S(-1)的白噪声泛函, 且A0(t),A1(t), B0(t),B1(t),B2(t)均不等于零. Wick 型随机Gardner 方程（5）常见于流体力学、等离子物理学和量子场论等领域, 是带有随机项和随机系数的偏微分方程, 由于加入了随机项, 求出的精确解是带有白噪声的泛函解, 也就是带有随机项的解. 因此,研究方程（5）具有重大的应用意义.

1 预备知识

1.1 Wick-型乘积与Hermite变换

定义1[18]给定Φ ∈L2(u), 对于P ∈R,Sp：=Φ ∈L2(u), ‖ Φ＜+∞, 称(S)1=⋂S-P为Kondratiev 测度空间函数, u表示概率测度, Ca表示白噪声泛函, (S)p是(S)-p的对偶, 称S-1=⋂S-P为Kondratiev 分 布 空 间. 设F=aαHα) 和G=bβHβ)为给定Kondratiev 分布空间S-1中的两个元, 且aα,bβ∈Rn, 则F 和G 的Wick 积 被 定 义 为:F ⋄G=aα,bβ)Hα+β，其 中Hα,Hβ为 白 噪 声 函数,(aα,bβ)为RN上的内积.

定义2[18]当F=(aαHα) ∈(S)-1, aα∈RN时, 定义F 的Hermite 变换F(z)=aαzα∈CN, 其中Z=(z1,z2,…)∈CN, zα=(…(…,|α|=|α1|+|α2|+…+|αn|+….

1.2 函数展开法

利用函数展开法求解非线性偏微分方程

的精确解,主要步骤如下：

步骤1:进行行波变换

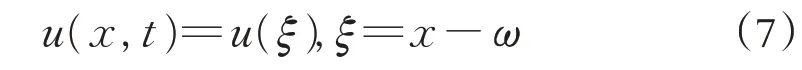
其中k,ω 为待定常数, ξ0为任意常数, 方程（3）就可转化为只含行波变量ξ的常微分方程：

步骤2:假设方程（8）的解可表示为多项式形式:

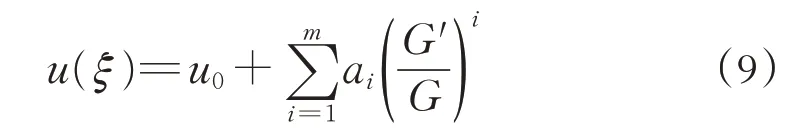
其中G=G(ξ)满足二阶线性常微分方程

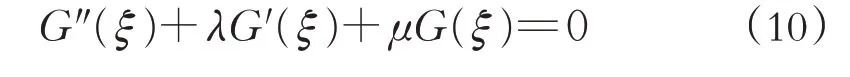
方程（9）和方程（10）中的a-m,…,a0,…,am,λ,μ为待定常数.记u(ξ)的幂次为则最高阶导数项和非线性项的次数分别为:

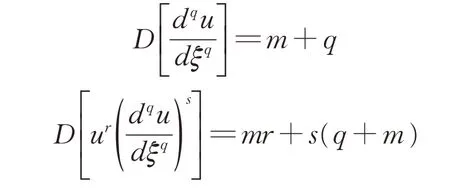
根据齐次平衡原则平衡（8）式中最高阶导数项和非线性项.由方程（10）可知

步骤3: 将式（9）代入式（8）, 运用式（10）和式（9）合并相同幂次项, 方程（8）左端就变成一个多项式, 令该多项式的各阶幂次的系数为零, 导出关于ai(i=-m,…,0,…,m),k,ω,λ,μ的代数方程.

步骤4: 求解步骤3 中建立的含ai(i=-m,…,0,…,m),k,ω,λ,μ 的代数方程, 解方程（10）,联立式（8）-（11）,即可获得方程（5）的行波解.

解常微分方程（10）得到通解G(ξ), 则可得到( G"(ξ)/G(ξ) ),其对应有以下三种形式：

1.3 求解Wick型随机偏微分方程的步骤

对于Wick型随机偏微分方程

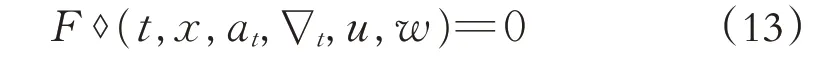
通过Hermite 变换, 由Wick 乘积变为普通意义下的乘积

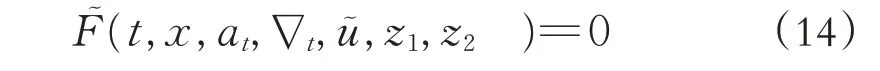
其中u͂是u 的Hermite 变换. 方程（14）通过Hermite变换得到随机偏微分方程

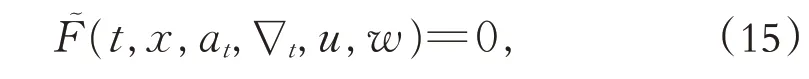
其中Z1,Z2…为复数. 通过函数展开法可找到式（12）的解.

引理1[19]假设存在有界开集,G ∈(R×R+)及 q ＞0, r ＞0，且 假 定 u(t,x,z),ut(t,x,z),ux(t,x,z)及uxxt(t,x,z)对(t,x,z)∈G×( )kq(r)一致有界, 对(t,x)∈G 连续, z ∈kq(r). 由文献[19]可 知, 存 在 U(t,x)∈S(-1)使 得 u(t,x,z)=u͂(t,x)(z), 其中U(t,x)是对应方程在空间S-1上的强解.

根据引理1的条件,使用Hermite变换的逆变换可得式（10）的精确解.

2 一类Wick-型变系数随机Gardner 方程的精确解实例

对于Wick-型变系数随机混合Gardner 方程（5）,利用Hermite变换由Wick型乘积化为普通乘积的形式为所对应的偏微分方程:

其中A0(t),A1(t),B0(t),B1(t),B2(t)都是关于t 的函数.

为简便,记A0(t)=a(t),A1(t)=b(t),B0(t)=d(t),B1(t)=f(t),B2(t)=h(t),则式（16）化为

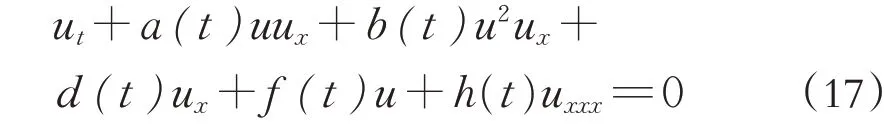
其中a(t),b(t),d(t),f(t),h(t)是关于t 的函数. 假设方程（17）具有的解的形式为

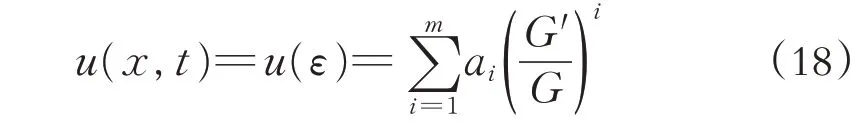
计算u"(ε),u2(ε),u"(ε), 将式（18）代入式（17）,合并i=0,1,2,3,4)的相同次幂次项系数,并令各幂次项系数为零, 得到关于a0(t),a1(t),C(t),k(t)的不定方程组

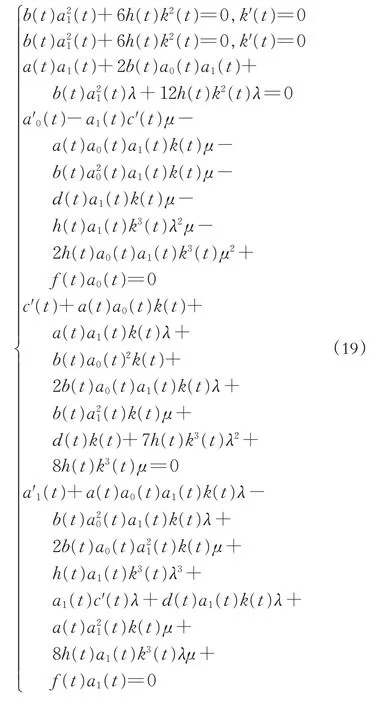
求解方程组（19）, 由a(t),b(t),f(t),h(t)以及ε,λ,K,μ表示出a1(t),c(t),k(t)得：

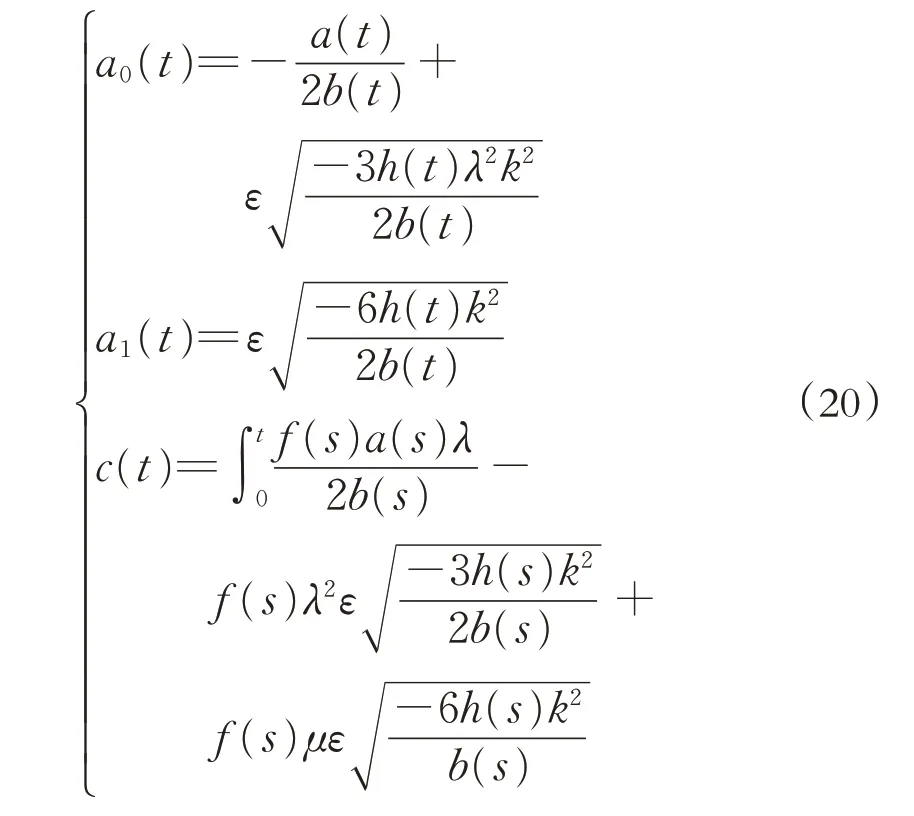
其中k(t)=k,ε=±1,k,a,b是任意常数.

将方程组的解式（20）带入到式（12）, 分类讨论从而得到方程（17）的精确解:

情况一: 当λ2-4μ=0 时可得方程（17）对应的有理函数解为:

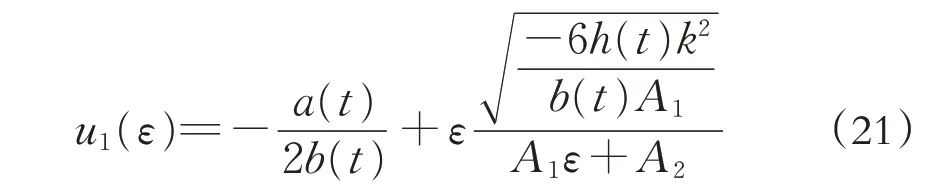
情况二: 当λ2-4μ ＜0 时, 可得方程（17）对应的有三角函数解为:

情况三: 当λ2-4μ ＞0 时, 可得方程（17）对应的有双曲函数解为:

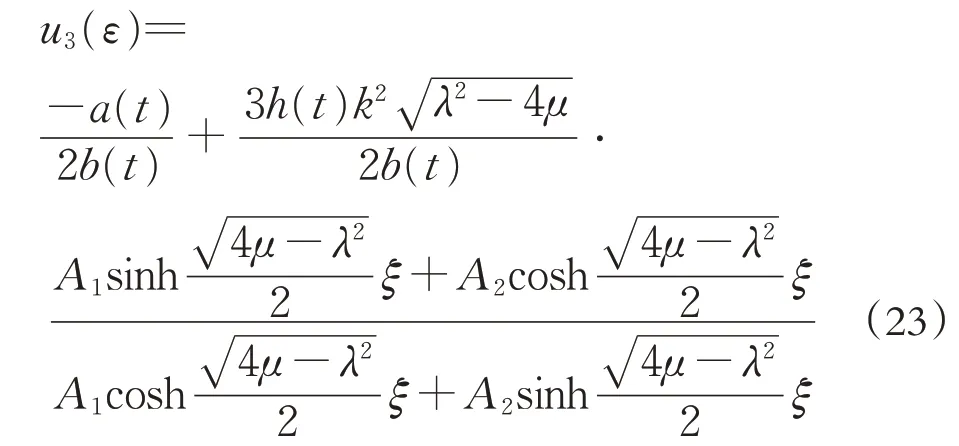
令u(t,x,z)为u(ε)的Hermite 逆变换, 由引理1可知:

①式（21）对应的方程（3）的有理白噪声泛函解为:

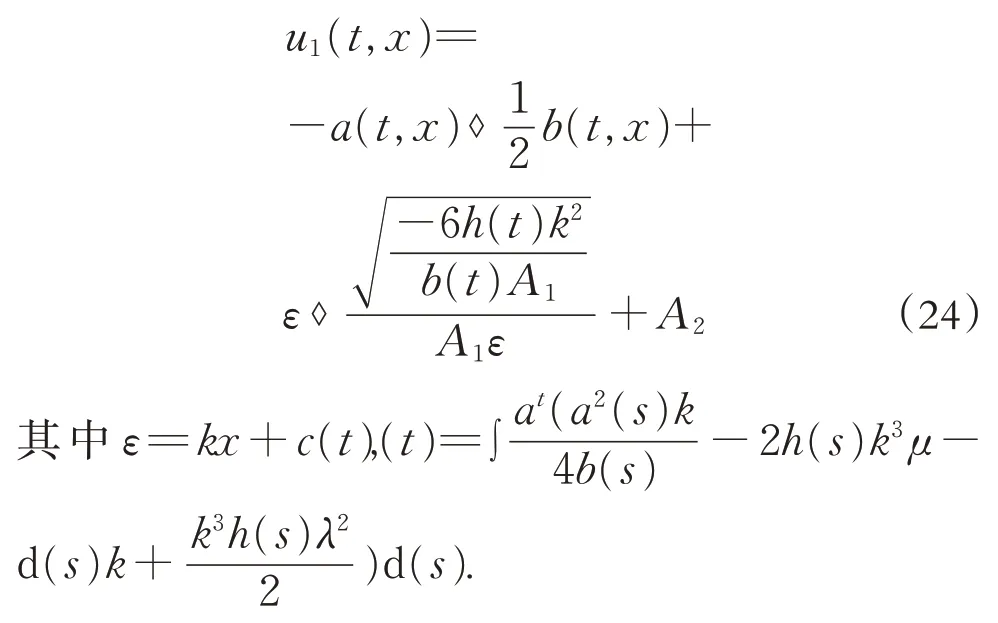
②式（22）对应的方程（3）的三角白噪声泛函解为：

③式（23）对应的方程（3）的双曲白噪声泛函解为:

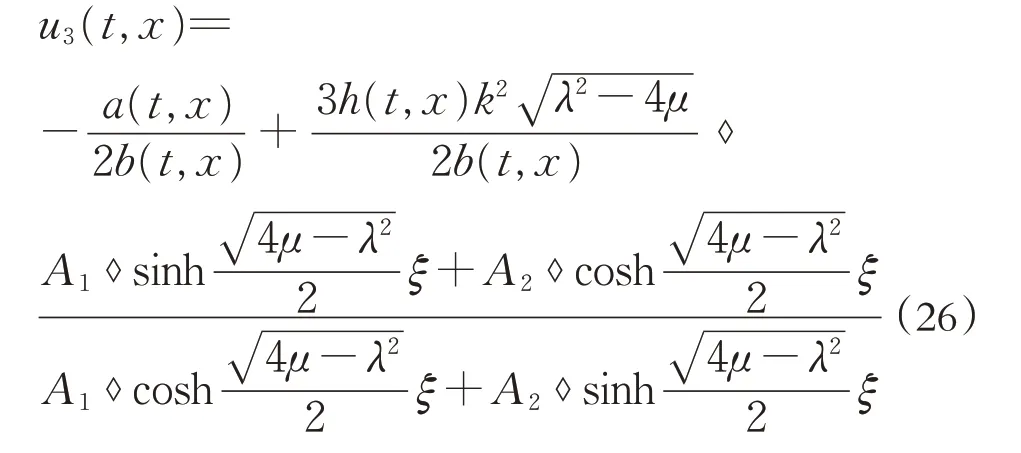
3 结语

本文利用Hermit 变换将Wick 型随机Gardner方程转化为偏微分方程, 同时利用函数展开法, 给出了有理函数解、三角函数解和双曲函数解,然后利用Hermit 变换的逆变换将这些解转化为Wick 型随机Gardner 方程的对应的泛函白噪声解. 对于随机方程（5）得到的解（24）（25）（26）,到目前为止在其他文献之中还未曾出现过.下一步的工作可以继续使用这种方法研究其它Wick-型随机分数阶方程或方程组的精确解.