Martin-Hou剖析和改进状态方程方法的研究进展
赵文英 孙晓岩 项曙光


摘 要:分析總结了Martin和Hou对立方型和多参数状态方程的研究方法。PVT关系是Martin剖析立方型状态方程和求解多参数状态方程系数的基础。研究了Martin从体积平移和压缩因子Zc值两个角度剖析和改进立方型状态方程的方法,概述了Martin和Hou提出适用于气体和改进用于液相和固相体系的多参数状态方程的方法。Martin-Hou (MH)多参数状态方程提高了对热力学性质的预测精度。研究Martin对基本热力学性质和立方型状态方程的剖析方法及多参数状态方程的改进方法,有助于研究者改进和提出新的状态方程模型。
关 键 词:热力学基本关系;立方型状态方程;MH多参数状态方程;研究进展
中图分类号:TQ013.1 文献标识码: A 文章编号: 1671-0460(2019)11-2678-05
Research Progress of Martin-Hous Method for
Analysis and Modification of State Equation
ZHAO Wen-ying1,2, SUN Xiao-yan2, XIANG Shu-guang1,2
(1. Qilu Normal University, Shandong Jinan 250200, China;
2. Qingdao University of Science and Technology, Shandong Qingdao 266042, China)
Abstract: Martin-Hous method for the analysis of the cubic and multi-parameter equation of state (EoS) was discussed. The relationship of pressure, liquid volume and temperature (PVT) is the foundation for the dissection of cubic EoS and the solution of the coefficients of multi-parameter EoS. The Martins methods of volume translation and the sum value of compressibility factor Zc for the analysis and modification of the cubic EoS were studied. The Martins idea for multi-parameter EoS for gas phase, liquid phase and solid systems was summarized. The multi-parameter EoS improved the predictive accuracy of the thermodynamic properties of non-polar, weakly polar and polar compounds. The research on the Martin-Hous method for the dissection of the relationship of thermodynamic properties, the cubic EoS, and the modification of the multi-parameter EoS, is beneficial for the modification of EoS and development of new EoS.
Key words: Relationship of thermodynamic properties; Cubic EoS; Multi-parameter EoS; Research progress
状态方程是热力学性质计算的模型,方程形式影响热力学性质的计算精度[1]。Van der Waals (1873)立方型状态方程是最早用于实际气体热力学性质计算的模型[2],但计算结果偏差较大。在VDW基础上改进的SRK[3]、PR[4]、PT[5]等EoS提高了计算精度。Martin (1967)对状态方程从数学角度上的分析有利于掌握状态方程改进的方向[6,7]。Martin对立方型EoS的剖析和对多参数EoS系数的求解根据基本的PVT关系得出的,这是热力学研究的基础。具有理论依据的多参数Virial状态方程是Martin和Hou提出多参数EoS的基础,Martin-Hou (MH) EoS经过改进后适用于汽、液、固相[8-12],其计算精度较高,适用范围广,但方程参数多,形式复杂,计算时间长,在实际和模拟计算中较少。
本文从介绍Martin分析热力学基本关系的角度入手,阐明Martin剖析立方型状态方程的思路并综述MH多参数EoS的研究进展,为多参数状态方程和立方型状态方程的发展指明方向和提供借鉴。近些年来,对MH EoS的综述性报道较少,朱兆友等(2011)[13]发表了一篇MH多参数EoS的基本形式、存在问题及应用的综述性报道。
热力学基本关系是热力学研究的基础,充分理解并灵活运用PVT关系,是研究热力学及改进状态方程的基础。
1 热力学基本关系
Martin (1967)详细阐述了P-V、P-T、通用压缩因子、压力体积微分及通用蒸汽压曲线5张图的内涵。这是剖析立方型EoS和求解多参数EoS系数的基础[8]。P-V图是热力学研究中应用最多的关系图[6]。P-V图上的临界点是状态方程研究的起点。100多年前Van der Waals提出了实际气体的状态方程[2]:
![]() (1)
(1)
等温线的临界点是水平斜率点和曲线凹凸转折点,其一阶和二阶导数为零:
![]() (2)
(2)
![]() (3)
(3)
Van der Waals根据临界点的数学性质,提出的这两个通用关系式,用于求解MH-55多参数状态方程的系数。1967年Martin对状态方程的剖析也自此开始。
在P-T图中观察到的是等容线。曾认为P-T图中所有的等容线都是直线,但实际上只有低压下的大体积,临界体积,高温下所有体积的等容线可以被看作直线,二阶导数为0。当对比温度Tr<2~2.5时,P-T图中的等容线在V>Vc时略微向下弯曲,在Vc~Vc/1.8之间略向上弯曲,在V<Vc/1.8时几乎是直线且略向下弯曲。当对比温度Tr >2~2.5时,几乎所有的等容线都向下弯曲。因等容线的弯曲效应很小,当对状态方程的预测精度要求不高时,可以假定所有的等容线都是直线,因此引力项的温度函数可表示为A+BT的线性形式[7]。
通用压缩因子图或z图是压缩因子与对比压力的关系图。在z图中,Martin研究了P=0点的斜率、剩余体积,波义尔温度点、临界点的范围、Tr=0.8的等温线切线及不同对比温度时等温线的特点。当压力趋向于零时,不论温度如何,所有气体都遵循理想气体定律,即Z=PV/(RT)=1。但当P=0时,V≠RT/P,这看上去是矛盾的。通过定义压缩因子图上任一点(P0,Z0)的微分,推导得出:
![]() ,当P=0 (4)
,当P=0 (4)
α定义为剩余体积(RT/P-V),α与压缩因子图中的等温线斜率相关,在P=0时,斜率不为零,α是一个有限值。等温线斜率为零时对应的温度为波义尔温度(Tb)。N2,CO,CH4的波义尔温度一般在Tr=2.5。临界温度很低的物质,如H2,波义尔温度大约为Tr=3.3。臨界温度较高物质的没有波义尔温度数据。大多数物质的波义尔温度在Tr<2.5。在通用压缩因子图中,临界点两侧相当温度范围内的临界等温线是直线。zc和z=1.0,Pr=0点的连线与Tr=0.8的等温线相切。Tr=1.1~1.2的等温线穿过最低点且有转折点。波义尔温度以上的等温线几乎是直线。Pr≈10的所有等温线的z=1.1~1.2。
分析一阶到五阶压力对体积的微分关系图可知,如果三阶导数为零,则四阶导数一定为零,五阶导数一定为负值或零。如果四阶导数为零,则三阶导数必为负值才能保证曲线在临界点正确的转折。压力对体积微分关系的正确趋势是一阶和二阶导数都为零,三阶导数为负值或零,四阶导数为零,若存在高阶导数,其影响也很小;对于五阶、六阶导数的研究很少。
通用对比蒸汽压曲线图中每一条曲线代表不同的物质,如果两种不同的物质在任何的点都落在相同的曲线上,它们将在全温度范围内一致。若已知临界温度和临界压力以及蒸汽压曲线上的任一点,根据对比蒸汽压曲线图可得到未知的蒸气压数据,用于预测临界点蒸气压曲线的斜率。穿过临界点(Tr=1,Pr=1)的每一条曲线都有唯一的斜率,即![]() ,简化得
,简化得![]() 。写成P对T的导数,即为
。写成P对T的导数,即为![]() 。PVT关系图中蕴含相关信息是状态方程剖析、改进的基础,也是多参数EoS系数求解的依据。
。PVT关系图中蕴含相关信息是状态方程剖析、改进的基础,也是多参数EoS系数求解的依据。
2 Martin对立方型状态方程的剖析
Martin分别于1967年和1979年对状态方程从不同角度进行了剖析。Martin(1967)从Van der Waals状态方程着手[6],根据P-V图临界点的性质对立方型状态方程进行了剖析。Martin(1979)从总包型状态方程入手[7],结合第二维里系数和zc之和的关系对状态方程进行了剖析,并提出新的两参数状态方程。
2.1 体积平移法剖析立方型状态方程
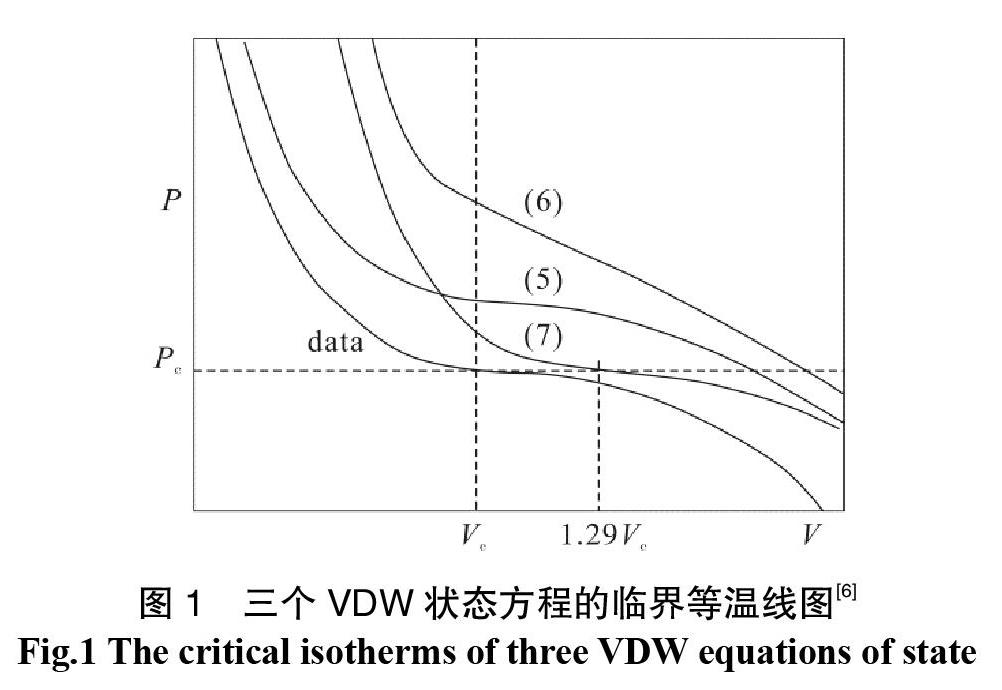
Martin(1967)从Van der Waals状态方程入手[6],由临界点方程(2)和(3)的关系推导出系数a和b的关联式。任意选择Pc、Vc、Tc中两个变量得到a和b不同的参数表达式及不同形式的状态方程,及不同的临界等温线(图1)。
与实验得到的临界等温线比较,发现方程(6)的曲线趋势不对,方程(5)进行压力垂直调整在大体积时会产生负值,方程(7)在体积平移时能更好的表示真实的PVT性质。
因此,Martin在方程(1)的体积项中增加一常数c得到方程(8),通过体积平移实现计算与实验的临界等温线吻合:
![]() (8)
(8)
假定c=![]() ,方程(8)的臨界点将准确的落在真实的临界点上,计算值
,方程(8)的臨界点将准确的落在真实的临界点上,计算值![]() 是0.29。但按照
是0.29。但按照![]() =0.29绘制出的临界等温线较实验值偏小。如果体积平移使计算的
=0.29绘制出的临界等温线较实验值偏小。如果体积平移使计算的![]() =1/3,得到临界等温线与实验的吻合很好;实际上,
=1/3,得到临界等温线与实验的吻合很好;实际上,![]() =1/3对于氩气是最好的,为了使数字更加简化,通常用
=1/3对于氩气是最好的,为了使数字更加简化,通常用![]() =0.335代替1/3。但对于其它
=0.335代替1/3。但对于其它![]() <0.291的物质,
<0.291的物质,![]() 略小一些更好。
略小一些更好。
為了考察远离临界温度的情况,将所有的等容线看成是直线,将温度函数a表示为A+BT的线性形式,根据通用蒸汽压曲线图及Tr=1的条件,解出A和B值,得到:
![]() (9)
(9)
与指数形式温度函数(Tr0.5)的RK方程进行比较,发现线性或指数形式的温度函数预测精度相近,方程(9)在ρr<1.6略好,RK方程在更高密度时较好。二者在有限范围内预测精度都很好,但是在宽范围内预测结果偏差较大。
为了验证体积平移法的可行性,Martin比较了多参数Virial方程的5项、7项、9项、11项、17项式及增加了体积b和指数项的改进形式。比较低于和高于临界点的全部数据,发现改进的方程明显优于7项维里式;达到1.8ρc时,计算精度优于11项式,与17项式相当。
2.2 压缩因子法剖析状态方程
Martin(1979)的文献中用总包型状态方程[7]:
![]() (10)
(10)
概括了现有应用广泛的状态方程,如Virial方程三项截断式,LE,RK,VDW,Martin,PR,将系数简化即可得到相应的状态方程。Martin通过推导得到Zc总和计算公式:
![]() (11)
(11)
与
![]() (12)
(12)
Martin通过第二维里系数和实验![]() 得到36种物质∑实验的平均值为0.62,并与不同方程推算得到的∑计算进行比较,证明方程预测结果与实验值之间误差较大的是因为∑计算与∑实验=0.62的差值较大。
得到36种物质∑实验的平均值为0.62,并与不同方程推算得到的∑计算进行比较,证明方程预测结果与实验值之间误差较大的是因为∑计算与∑实验=0.62的差值较大。
令Martin总包型方程(13)中的δ=0并简化为无因次的对比态形式,得到:
![]() (13)
(13)
Martin假定Zc=0.25,计算出αPc/R2Tc2及∑计算值,并与∑实验=0.62比较,找出Zc值大小变化的方向,发现Zc=1/3时∑计算趋于0.62。低于临界密度时,将Zc=0.23、0.25、0.27分别用于方程(13),得出Zc为0.23时出现负偏差,Zc为0.27时出现正偏差,Zc为0.25偏差小于1%,是适于方程(13)的最佳值;但高于临界密度时发现所有的Zc值都偏差较大。总的来说,Zc=0.25,体积平移0.082的方程是最优化的,即:
![]() (14)
(14)
Martin用∑计算需要满足趋于0.62的规律,验证现有状态方程的可靠性。比较RK方程的Zc=1/3和PR的Zc=0.307,方程(14)的Zc=0.332,发现RK与Martin的Zc的值更接近;而RK EoS的∑计算=0.674173,PR的∑计算=0.68684,都高于Martin的∑计算=0.671875,远离期望值0.62。通过∑计算看出,PR最差,RK稍好,但都不如Martin EoS。同样比较Viril方程三项截断式和LE方程,从Zc=1/3入手,依据Martin推导∑计算的思路,简化状态方程,并与立方型状态方程比较高于和低于临界点的预测结果,发现临界密度上下的预测精度不能兼顾,计算精度与立方型状态方程相近,不如Martin EoS精度高。
Martin將方程(14)中的引力项表示为最简单的温度函数形式![]() :
:
![]() (15)
(15)
为了研究指数n,Martin研究了对比蒸汽压曲线图的斜率M。根据氩气临界等容线的斜率是6.1,推导出方程(15)的一阶导,得到![]() 的微分关系。Martin分析了方程的一阶导的模拟曲线与实验曲线形状的关系,指出状态方程的热力学模型仅是近似的工作。虽然热力学模型的计算结果不很精确,但在一定范围内进行有效计算是能够满足要求的。
的微分关系。Martin分析了方程的一阶导的模拟曲线与实验曲线形状的关系,指出状态方程的热力学模型仅是近似的工作。虽然热力学模型的计算结果不很精确,但在一定范围内进行有效计算是能够满足要求的。
Martin用方程(15)推导得出适合氩气的最佳n值,得出计算氩气最佳状态方程。列举的EoS对于氩气的预测结果都很接近,提出的方程更简单且准确。Martin比较了用不同状态方程对八氟环丁烷、异戊烷、三氟甲烷、氨等的测定结果,发现方程(15)的模拟结果是最准确的,因为方程(15)中的Zc和n值都是可调的。
Martin以Van der Waals EoS为例,从等温线的临界点入手推导,得出体积平移是改进VDW EoS使其符合实验数据的最佳方法。而1979年Martin提出新的总包型状态方程,从压缩因子总和的角度研究状态方程的计算精度,提出得出状态方程计算的与实验的最接近的Zc总和值,并以此为标准分析了列举的立方型状态方程和多参数状态方程截断式。Martin的这两篇对立方型状态方程剖析有理有据,推导符合逻辑,从数学意义上分析了状态方程,其研究思路是值得借鉴的。
3 Martin-Hou多参数状态方程
3.1 MH-55多参数状态方程
Martin和侯虞钧(1955)[8]在Virial方程的基础上提出了多参数状态方程,并根据PVT关系求解出多参数状态方程系数的解析解:
![]() (16)
(16)
方程(16)形式上与Virial方程类似,其中f2~f5的系数在BB和BWR的P = A + BT + C/T2的基础上,根据临界点以上温度曲线的形状修改函数形式为P=A+BT+Cexp(–kT/Tc)。方程中的f2~f5,A2,B2,C2,A3,B3,C3,A4,B5各系数根据第一部分的PVT关系求出。
Martin等(1959)[14]在MH-55状态方程中增加了A5和C5两项系数,将方程的适用范围扩展到1.4ρc,并给出了A3,B3,C3,A5,B5,C5的求解方法[13]。以二氧化碳为例,比较了方程修正前后的计算结果,发现低于临界密度时二者接近,高于1.2ρc时修订的MH EoS计算偏差小于原方程。
MH-55方程用于CO2,H2O,C6H6,N2,C2H6,H2S,C3H8时,最大偏差小于1%,当低于1.5ρc时,偏差很小。临界点的体积通常是很难测准的,一般是外推得到,5%的偏差很正常。
3.2 MH-81多参数状态方程
侯虞钧等(1981)[9]修正了MH-55多参数状态方程,将其适用扩展到液相区域。MH-81方程是在MH-55方程的基础上,在f4项中增加了B4项系数,方程成为:
![]() (17)
(17)
根据汽液两相在平衡状态时的条件求解B4项系数。由于B4项的增加,使得其它方程系数都有所变化,而不能像MH-55方程一样求出解析解。李诗纯等(2011)研究了参数m和B4的求解方法[15]。侯虞钧等将MH-81方程用于CO2汽相摩尔体积和液相摩尔体积的计算,发现计算误差明显减小,在低于300 atm时,偏差约为5%;在低于200atm时,偏差一般在2%~3%。虽然MH-81方程的计算精度提高,但f4项中的系数B4需要迭代计算得到,计算过程复杂,为应用带来困难。
吕秀阳和侯虞钧(1993)[11,12]对MH-81方程中的特性参数m、TB、T、β、K进行分析,研究特性参数对关联结果的影响,找出影响关联结果的关键因素,发现参数T是敏感参数,由于确定T的实验数据本身精度不高,因此可将T作为一个可调参数进行优化。m、K、β对关联结果的影响也很大,TB和不同的目标函数的形式对关联结果影响较小。文章还给出了MH常数是否合理的评价方法,方程求根方法,方程适用范围及方程应用的建议。
MH-81方程对CO2,n-C4H10,Ar,CH4,N2的饱和汽液相摩尔体积进行了计算,并与文献数据比较,发现MH-81方保持了汽相的精度,且显著提高了液相的计算精度。在两相共存区,液相摩尔体积的百分偏差最大不到10%,一般可以维持在5%以下。
3.3 MH-96多参数状态方程
侯虞钧等(1996)[10,16]继续改进MH-81方程,在方程中增加了f6和f7两项,并将其分母的b项改为bs,使其用于固相体系,方程如下:
 (18)
(18)
方程求解与MH-81方程类似,是利用三相点处的液固和汽固平衡关系,通过三层迭代求解A6和B7、B4的值。方程系数求解过程复杂,方程式本身也很复杂,这也是限制MH-81和MH-96状态方程在液相和固相体系中应用的主要因素。
MH-96状态方程计算了CO2,Ar,CH4,N2的饱和汽、液、固相摩尔体积,汽相摩尔体积偏差小于1%,液相小于5%,固相偏差最大在10%左右。自Martin提出的MH-55方程后,将实验和状态方程结合,用于不同物质的PVT行为[17],热容常数[18],汽化潛热[19,20],蒸汽压性质[21]等方面的计算,实验与计算结果比较接近,状态方程有应用价值。
3.4 缔合M-H状态方程
南延青和侯虞钧等(1997)[22]将MH-55方程与缔合理论结合得到一个新的缔合理论状态方程:
![]() (19)
(19)
式中n0為纯物质A没有缔合存在时的摩尔分数,nT为真实摩尔分数。当nT/n0=1时,恢复到MH方程状态。该方程用于水-醇-酸体系饱和蒸汽压的计算结果偏差小于1%,汽相摩尔体积的偏差小于2%,液相摩尔体积的偏差小于5%。南延青、侯虞钧和郝力生等(2001-2004)[10,11]将缔合MH状态方程应用于缔合化合物或羧酸-烃或醇-烃等混合物体系。
Martin-Hou状态方程具有较强的理论基础。侯虞钧等(2002)[23,24]根据virial EoS的推导方式,从具有分子体积的准理想气体模型出发,利用正则分布和势能函数,通过适当简化,从理论上推导MH EoS,发现MH EoS与Virial EoS具有相同的理论基础。由于MH方程对分子间作用力做了合理的近似,避免了高阶Virial系数求解困难的问题,并在实际应用中取得成功。理论推导的MH方程与经验MH方程在求解第二Virial系数和流体分子的微观参数上均与实际数据吻合较好。
4 结论
Martin和侯虞钧系列文献解析了PVT之间的内在联系。Martin对两项和三项状态方程从两个不同角度进行了剖析: (1)从等温线临界点的性质着手,剖析了VDW立方型状态方程,发现体积平移是改变VDW EoS关联精度的最佳方法,并将体积平移用于多参数Virial方程进行验证;(2)Martin研究发现实验压缩因子和第二维里系数的加和通常为0.62,与两项或三项状态方程计算的压缩因子和第二维里系数的加和值进行比较,证明原有状态方程对热力学性质预测产生偏差的原因是计算的压缩因子与第二维里系数的总和与实验值0.62偏差较大。Martin对于PVT热力学基本关系的分析充分,理解到位,思路清晰,掌握Martin分析热力学性质及剖析立方型状态的思想,有助于提出和改进新的立方型状态方程。
Martin-Hou的另一贡献是在Virial方程的基础上提出了适用于气体的新多参数状态方程,即MH-55状态方程,并利用PVT之间的关系求解出多参数状态方程系数的解析解。侯虞钧等在MH-55状态方程的基础上不断改进,扩展应用于液相体系和固相体系,并研究了其中的各参数对状态方程预测能力的影响程度。虽然多参数状态方程形式复杂,在求解方面需要迭代计算,在实际应用中较少,但是多参数状态方程有较强的理论基础,对于新的多参数状态方程的开发具有指导意义。
参考文献:
[1]陈磊,冷明,任帅,等. 状态方程在气固相平衡计算中的应用[J]. 当代化工,2014,(06):1121-1123,1129.
[2]Van Der Waals J. H. On the Continuity of the Gaseous and Liquid State[D]. Holland: Leiden University, 1873.
[3]Soave G. Equilibrium constants from a modified Redlich-Kwong equation of state[J]. Chemical Engineering Science, 1972, 27(6): 1197-1203.
[4]Peng D. Y., Robinson D. B. A New Two-Constant Equation of State[J]. Industrial & Engineering Chemistry Fundamentals, 1976, 15(1): 59-64.
[5]Patel N. C., Teja A. S. A new cubic equation of state for fluids and fluid mixtures[J]. Chemical Engineering Science, 1982, 37(3): 463-473.
[6]Martin J. J. Equations of state[J]. Industrial and Engeering Chemistry, 1967, 59(12): 34-52.
[7]Martin J. J. Cubic equations of state - which?[J]. Industrial & Engineering Chemistry Fundamentals, 1979, 18: 81-96.
[8]Martin J. J., Hou Y. C. Development of an equation of state for gases[J]. AIChE Journal, 1955, 1(2): 142-151.
[9]侯虞钧, 张彬, 唐宏青. 马丁-侯状态方程向液相发展[J]. 化工学报, 1981, 32(1): 1-10.
[10]侯虞钧, 陈新志, 周浩. 马丁-侯状态方程向固相发展[J]. 高校化学工程学报, 1996, (3): 2-9.
[11]吕秀阳, 侯虞钧. 对马丁-侯(81)型状态方程的进一步研究[J]. 浙江化工, 1993, (01): 6-9.
[12]吕秀阳, 侯虞钧. 对马丁一侯(81)型状态方程的进一步研究(连载)[J]. 浙江化工, 1993, (02): 12-16.
[13]朱兆友, 張方坤, 徐超. 马丁-侯(M-H)状态方程研究应用进展[J]. 上海化工, 2011, (07): 12-15.
[14]Martin J J, Kapoor R M, De N N. An improved equation of state for gases[J]. Aiche Journal, 1959, 5(2): 159-160.
[15]李诗纯, 魏顺安, 张建, 等. 马丁-侯方程中参数m和B4的直接求取[J]. 高校化学工程学报, 2011, (01): 7-10.
[16]侯虞钧, 陈新志. 马丁-侯状态方程向固相发展[J]. 高校化学工程学报, 1996, (3): 217-224.
[17]Martin J. J., Bhada R. K. Pressure‐volume‐temperature behavior of carbon tetrafluoride using a variable‐volume cell of bellows design[J]. AIChE Journal, 1971, 17(3): 683-688.
[18]Hwang Y. T., Martin J. J. The constant‐volume heat capacity of gaseous tetrafluoromethane[J]. AIChE Journal, 1964, 10(1): 89-91.
[19]Martin J. J., Edwards J. B. Correlation of latent heats of vaporization[J]. AIChE Journal, 1965, 11(2): 331-333.
[20]Jr C. G. V., Martin J. J. Heat of Vaporization and Vapor Pressure of 1,4-Dioxane[J]. Journal of Chemical & Engineering Data, 1963, 8(1): 74-75.
[21]Hou Y. J., Martin J. J. Physical and thermodynamic properties of trifluoromethane[J]. AIChE Journal, 1959, 5(1): 125-129.
[22]南延青, 侯虞钧, 俞庆森. 缔合马丁-侯状态方程Ⅰ方程的建立[J]. 物理化学学报, 1997, 13(8): 725-731.
[23]李新华, 陈新志, 侯虞钧. M—H EoS的物理意义[J]. 浙江大学学报(工学版), 2002, 36(6): 694-697.
[24]李新华, 侯虞钧. M-H-EoS的理论基础[J]. 化工学报, 2002, 53(8): 819-823.

