基于改进椭圆权重模型的射频层析成像定位方法

李莉，柯炜，许桁宽，于坤良，王彦力

（1. 南通科技职业学院机电与交通工程学院，江苏 南通 226007；

2. 南京师范大学物理科学与技术学院江苏省光电技术重点实验室，江苏 南京 210023；

3. 江苏省地理信息资源开发与利用协同创新中心，江苏 南京 210023）

1 引言

与传统定位方式要求定位目标必须携带与定位系统相匹配的定位设备（如GPS接收机、手机等）不同，免携带设备定位（DFL，device-free localization）无需定位目标携带任何定位装置，也无需定位目标主动参与定位过程[1-2]，因此DFL在人员搜救、非法入侵检测等特殊情况下的老人照料等传统定位方法无法实现的定位领域可以发挥重要作用。相比于现有的基于摄像头、超宽带雷达、红外、超声波等技术的免携带设备定位[3-5]，基于无线传感器网络的 DFL技术因其成本低、通用性好并能够穿透墙壁及烟雾进行定位等优点，成为当前 DFL领域的一个研究热点。同时，随着研究的深入，相关技术已经推广到了人体姿态识别和心率测量[6]。因此，免携带设备定位技术及其衍生技术有着广阔的应用前景。

目前，基于无线传感器网络的DFL方法大致可以分成3类，即指纹定位方法[7-8]、RTI方法[9-10]和几何定位方法[11-12]。指纹基的DFL要求事先建立指纹数据库，并且随着环境的变化需要不时进行数据库更新，对人力和物力投入要求较高。几何基的DFL将链路连接表示成直线段，利用链路之间的几何关系进行定位，该类方法虽然无需建立指纹数据库，但容易受多径传播影响。RTI方法最早由犹他大学的Patwari等[9-10]提出，通过在目标区域的边缘部署若干收发节点，根据每个节点接收到的信号强度（RSS，received signal strength）的变化来反映目标的影响，并借鉴医学CT（computed tomography）思想用反演图像的方式呈现出定位结果，该方法由于其直观性强而受到较多关注。RTI方法的核心是通过一个阴影权重模型，构建RSS值变化与目标位置之间的关系，然后通过正则化方法反演出位置图像。因此，阴影权重模型成为决定RTI成像质量的关键因素之一，因而也成为RTI研究的重点之一。从最早Zhang等[9]提出的矩形模型开始到广泛应用的椭圆模型，都只单纯考虑了链路长度对于权重的影响，忽略了被定位目标与链路之间的距离关系。更为重要的是，这些模型认为椭圆内所有格点的权重相同，并不符合实际情况。为此，Hamilton等[13]提出了一种以包含目标的最小椭圆面积的倒数为权重值的IAEM（inverse area elliptical model）模型，一定程度上克服了原椭圆模型的缺点。最近菲涅耳衍射理论被越来越多地考虑，马鞍模型[14]和衍射模型[15-16]中均将菲涅耳衍射理论作为建模依据。但这些模型给出的不再是单纯的权值，而是具体的RSS变化量，已无法直接用到RTI成像。另外，由于测量噪声和异常链路测量的存在，利用任何一种权重模型所得成像结果都不可避免地存在着背景噪点，有时甚至还有伪目标出现在图像上，给真实目标的确定带来了较大困难。因此，如何去除背景干扰，也成为近年来RTI研究的热点问题。

本文针对上述2个问题，首先依据菲涅耳衍射理论提出双层椭圆阴影权重模型，以达到更精确描述RSS值变化与目标位置之间关系的目的；同时借鉴图像处理中前景提取方法，利用十字模型进行目标提取，进一步提高RTI成像质量和定位精度。

2 RTI基本原理与存在问题

2.1 RTI原理简介

假设定位区域周围布置了L个无线节点，一共可以组成M=(L-1)L条无线链路，并且将定位区域划分为N个网格，可以形象地将这些网格称为“像素”。相对于无目标时空区域，当待测目标进入定位区域时，会引起RSS值的变化，如式(1)所示。

其中，y表示目标进入定位区域前后RSS测量的差值矢量，W是阴影权重矩阵，x是待估计的像素矢量，n表示噪声矢量。

利用正则化理论求解上式可得[9]

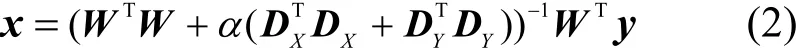
其中，α为正则常数，DX，DY为正则矩阵。

2.2 现有椭圆模型的不足

现有的椭圆阴影权重模型是以一对收发节点为焦点构成一个椭圆，椭圆外部的像素点权值设为0，椭圆内部的像素点权值依据式(3)计算得到

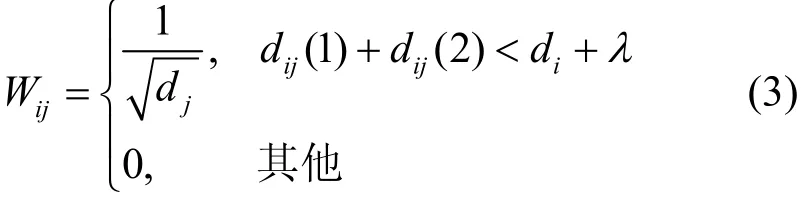
其中，di表示第i条链路长度，dij(1)，dij(2)分别为第j个像素点到组成链路两节点的距离，λ为椭圆短轴长度，i为链路序号，j为像素点序号。

该权值的计算依据为链路越长，当该条链路与其他链路相交时的权重就应该越低。一般来说，目标遮挡一条短链路对 RSS值产生的影响要大于遮挡一条长链路产生的影响[9]，因此这种权值取法有一定的合理性。但是，许多实验[14-16]表明仅仅依靠链路的长短来确定权值是不够的。由于人距离收发节点的远近不同会导致对链路不同的影响，因此对于同一条链路，将椭圆内所有像素设为同样的权值是不符合实际情况的，也会导致成像效果的变差。

3 双层椭圆阴影权重模型

菲涅耳衍射理论认为空间任意一点处的辐射场，是包围波源的任意封闭面上产生的所有次波在该点所产生场叠加结果[17-18]。通过菲涅耳半波带法可以将链路周围的区域划分为若干个菲涅耳区，这些菲涅耳区是以收发节点为焦点的旋转椭球。若某点到收发节点的距离之和与链路长度相差n个半波长，则该点为第n菲涅耳区的边缘，而该椭球的短半轴长称为最大第n菲涅耳半径，如图1所示，其中S、R表示收发节点。

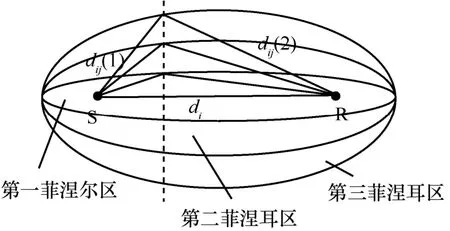
图1 菲涅耳区示意

通过菲涅耳半波带法可以论证某点的场主要取决于第一菲涅耳半波带，90%的能量都在第一菲涅耳区内传播[17-18]，因此，可以认为当目标遮挡住链路的第一菲涅耳区时，视为有效遮挡。而当目标处在第一菲涅耳区外部时，可以认为对链路测量值的影响很小，此时权值和椭圆模型一样均设为 0。下面重点分析第一菲涅耳区内的权值设定。

首先，对于同一条链路，在距离收发节点距离不同的位置对于RSS值影响是不同的。当人遮挡的面积占第一菲涅耳区某截面的百分比越大时，对RSS值的影响也越大。故下文讨论对于同一条链路，人在不同位置遮挡住的面积占第一菲涅耳区在该处的截面面积百分比的变化情况。图2中，将人近似视为圆柱体站在链路中，椭圆为第一菲涅耳区，截面图中 o为圆心，r1为第一菲涅耳半径，人的体宽设为h，阴影部分为遮挡部分可计算出人体所遮挡面积占第一菲涅耳区在该处截面面积的百分比为

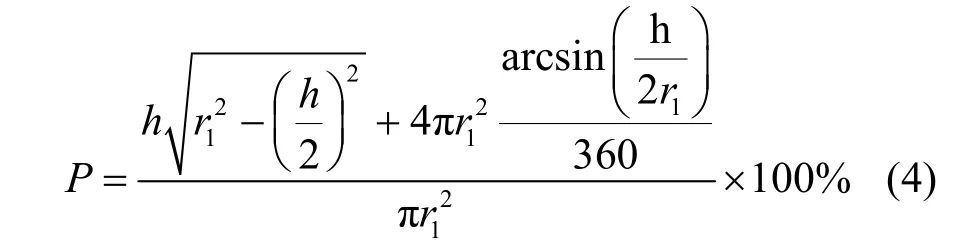
以下文使用的美国犹他大学实验室的实验场景为例，链路最短距离大约是2 m，最长距离大约是72 m，与此对应的最大第一菲涅耳半径为0.210 m到0.556 m。若把人的体宽取为0.3 m，则P关于r1的函数图像如图3所示，可见在此范围内，函数是单调下降的。

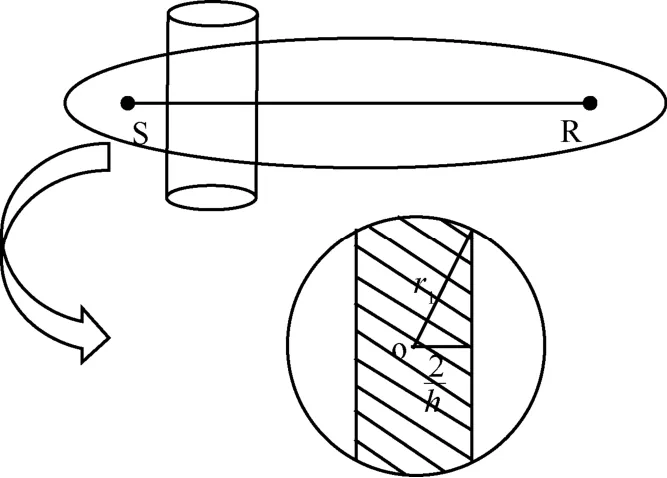
图2 人体影响示意

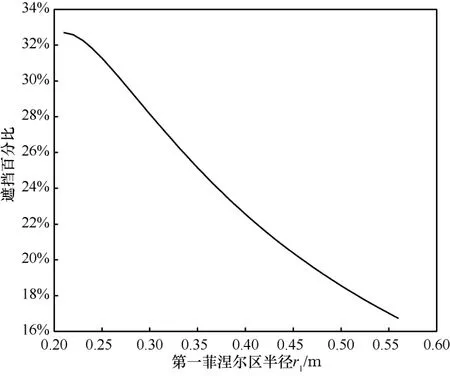
图3 人体遮挡面积与第一菲涅耳半径关系曲线

对于一条链路，收发节点处对应的第一菲涅耳半径最小，逐渐扩大到链路中点对应的最大菲涅耳半径，根据上图可知，随着第一菲涅耳半径的扩大，P越来越小，因此对RSS值的影响也越小，故可将像素点权值的大小设为与该点所对应第一菲涅耳半径的平方成反比。同时，考虑到对于同一条链路某位置的一个横截面，当人偏离链路时，遮挡的面积占截面百分比人恰好在链路上时相比更小，对信号传播的影响也越小。因此，结合菲涅耳半波带法不难发现，越远离链路的位置传输的能量越小，对信号传播的影响也越小。综合这两点：在同一截面，越靠近链路的位置对RSS值影响越大，应赋予更高的权值。由此引入传播主区的概念，对第一菲涅尔区靠近链路和远离链路区域的权值进行划分。传播主区是指第一菲涅耳区中面积占三分之一的空间区域，又称最小菲涅耳区[17-18]，因此通过赋予传播主区内的像素更大的权值来对第一菲涅耳区内的像素进一步划分，按照第一菲涅耳区域内权重的赋值方法，得到了新的权重模型：

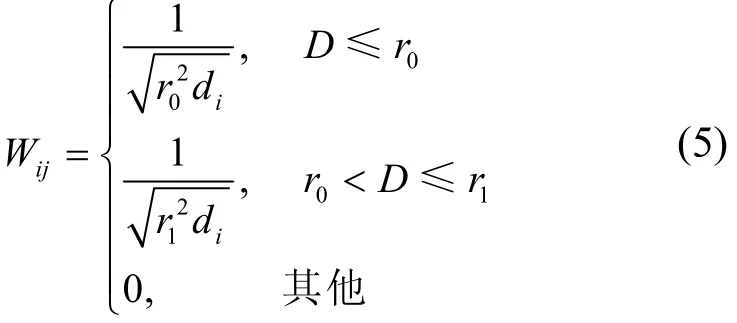
其中，r0和r1分别为第i条链路对应的最小菲涅耳半径和第一菲涅耳区半径，D为该像素点到链路的投影距离。菲涅耳半径的计算可参考文献[17-18]中的计算式。

4 前景目标提取算法

RTI依靠检测目标对无线链路RSS的影响来进行成像，但RSS极易受环境影响，甚至在无目标出现时，某些链路的RSS值也会出现变化，这些异常链路往往会造成虚假的伪目标像，从而容易引起对定位目标的误判，一旦误把伪目标位置判定为真实目标位置，则定位误差会急剧增大。为了消除伪目标的影响，本文借鉴图像处理中前景提取方法，利用十字模型进行目标提取。前景目标提取分为2个步骤。

步骤1由于RTI算法是通过反演成像进行定位的，图像亮度越高的区域就越可能是定位目标所在位置，因此对于亮度低于图像各像素均值的区域，无论其亮度如何，都可定义为背景。基于此分析，可以对所有像素点的亮度值求平均，低于平均值的像素点亮度信息设为 0，这一步初步消除了一部分背景噪点，但仍可能留下一些伪目标，需进一步后续处理。

步骤 2除了亮度足够高以外，多个高亮度像素集中的区域有更高的概率是定位目标所在区域，因为各类噪声的干扰很难产生相当于目标直接遮挡链路的影响，因此需要将高亮度像素集中的位置作为前景提取出来。由于算法采用的是椭圆模型，而若干椭圆相交的结果是一个近似于圆形的形状，这是算法本身提供的形状信息，可以借此对前景进行提取。对于在均值法消除背景中保留下来的高亮度噪声像素，其周围的像素必然不可能都是高亮度像素，因此把某个像素点的亮度值设为其本身与其一定大小的圆形邻域内的亮度值的乘积，由于在均值法消除背景的过程中已经把一部分背景的亮度值设为 0，因此只要某像素的圆形邻域内有一个像素的亮度值为 0，其亮度值就会变为零。而对于目标像素，其圆形邻域内都是亮度值较高的像素点，相乘后不可能变为 0，因此在这一步结束之后，图片上留下的目标即视为前景，即定位目标所在位置。

为了减少计算量，在实际操作过程中，不采用圆形邻域的亮度值乘积，而是用十字模型的亮度值乘积，因为圆形是一个高度对称的形状，因此采用正交的两条直径来表示圆形的特征，根据实验数据的验证，用此模型的效果与圆形邻域效果相似，且速度更快，计算式如式(6)所示。

其中，x(i,j)表示坐标为(i,j)的像素点的亮度值，当m=0时，n=-3，-2,…,2,3，当n=0时，m=-3，-2,…,2,3。十字模型如图4所示。十字长度可根据实验结果确定，主要取决于目标可能影响的区域大小，本文中将十字架长度定为7个像素。

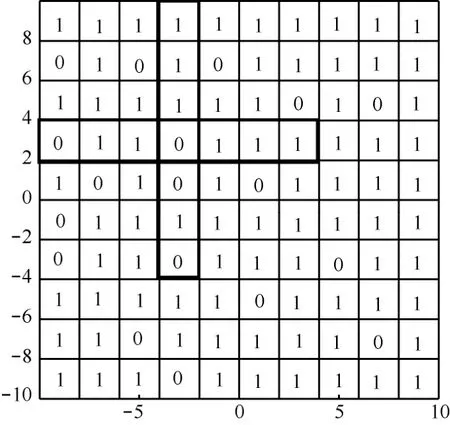
图4 十字模型示意

5 实验结果

为全面衡量本文方法的有效性，本文使用室内外不同环境的实验数据对不同模型的定位结果进行了对比分析。对于室外环境，首先选用了使用较广的公开数据源——美国犹他大学实验室的实测数据，以增强比较结果的权威性。该数据采集于室外有障碍物的小区域场景（如图5(a)所示），由28个工作在2.4 GHz频段无线节点组成的测量网络均匀部署在面积约为6.3 m×6.3 m的方形区域的周围，相邻节点之间距离约0.9 m。由于该定位区域面积较小，仅约40 m2，为了能进一步反映本文方法在大区域的定位性能，以 TI公司 2.4 GHz频段的CC2530芯片为基础自行设计了收发模块，并结合ZigBee协议构建了DFL定位系统。该系统由20个测量节点组成，均匀分布在室外10 m×10 m方形区域周围（如图5(b)所示），相邻节点之间距离为2 m。在室外定位的基础上，为了反映室内墙壁、玻璃等对RTI成像的影响，又在南京师范大学行健楼室内大厅选择5 m×5 m的方形区域，同样在周围均匀布置20个收发节点进行定位实验（如图5(c)所示），此时相邻节点之间距离为1 m。

图5 实验场景

5.1 室外小区域环境下定位性能比较

为了读者能直观地了解不同模型的定位性能，首先通过RTI成像图给出3种不同模型的定位效果。图6(a)、图6(c)、图6(e)分别是室外小区域环境中目标在（0.9 m，2.7 m）位置时分别用椭圆模型、马鞍模型、双层椭圆模型得到的RTI成像图。由图可以发现，椭圆模型、马鞍模型的成像图在左上角都有一个明显的伪目标存在，而用双层椭圆模型得到的 RTI图中则没有这个伪目标，而且背景更为清晰，这说明改进的双层椭圆模型能够更准确地反映目标对链路影响的权重关系。图6(b)、图6(d)、图6(f)是各模型加了十字模型提取前景后得到的定位图，由于室外环境障碍物较少，通过十字模型进行前景提取能比较完美地滤去背景噪点。

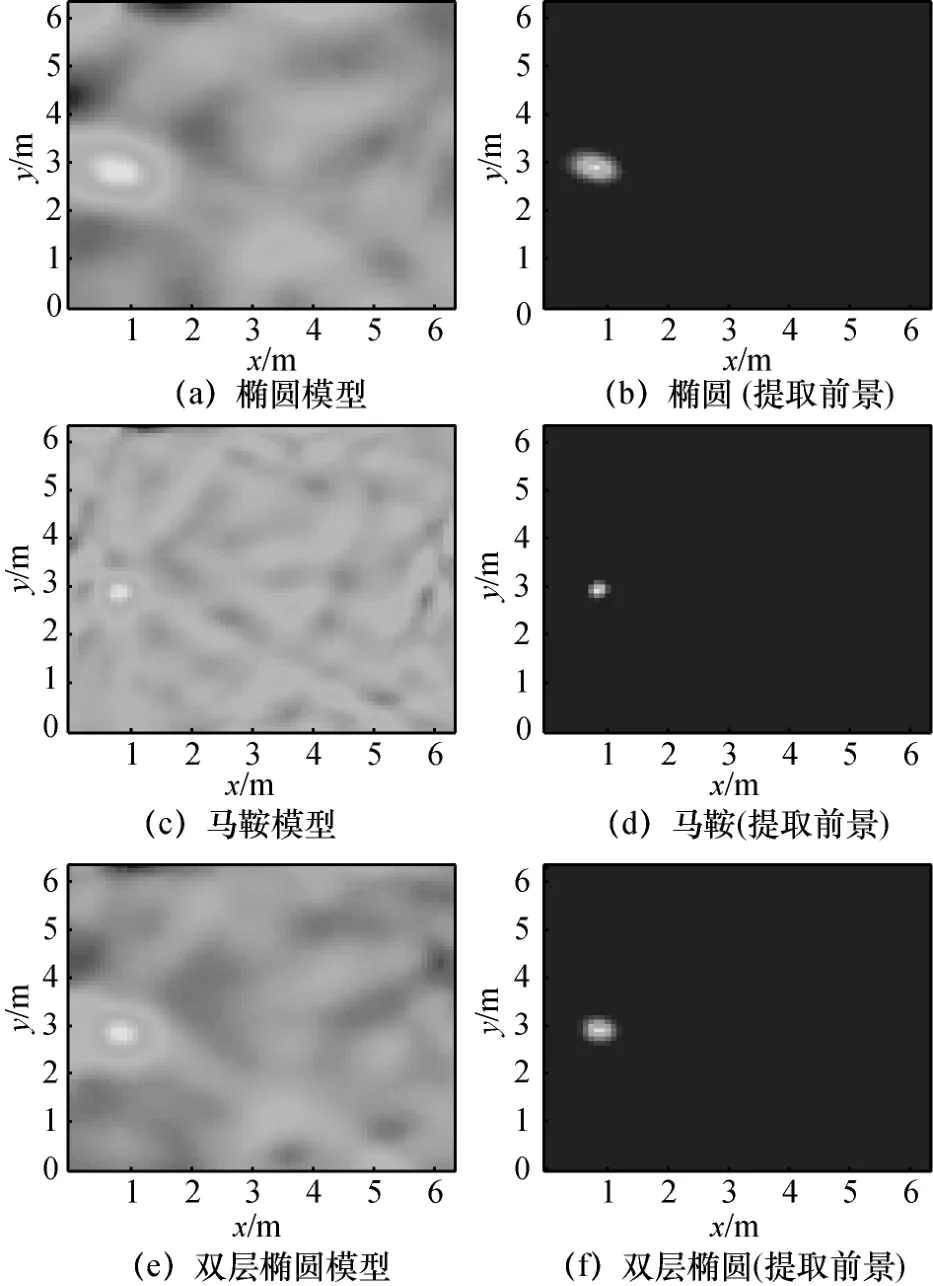
图6 室外小区域环境下3种模型的成像图比较

为了更全面反映定位性能，详细的统计结果如表1所示。按照RTI的常规做法，取亮度最高的像素点所在位置作为目标位置。在定位过程中，椭圆模型和马鞍模型都存在因为伪目标亮度高于目标亮度而导致定位失败的情况，此时会出现非常大的定位误差，而改进的双层椭圆模型没有出现这种情况。为了公平起见，表1中对于椭圆模型和马鞍模型同时给出了全部数据的统计结果和除去这些定位失败结果之后的统计结果。

表1 室外小区域环境下各模型定位误差统计结果

从表1可以看出，在没有经过前景提取时，由于易受伪目标影响，马鞍模型和椭圆模型的平均定位误差较大，在没有去除定位失败结果的情况下平均误差都接近1 m。本文提出的双层椭圆模型由于能更准确地反映目标对RSS变化的影响，所得背景较为干净，即使偶尔出现伪目标，其亮度一般也低于真实目标，不会出现误判。而椭圆模型和马鞍模型的背景较为复杂，即使在统计中已去除伪目标亮度值高于目标亮度的情况下，定位精度仍低于双层椭圆模型。

采用前景提取方法后，由于消除了一些伪目标，因此这几种模型的定位效果都要好于直接判断的结果。由于在室外小区域环境下原本双层椭圆模型的定位误差就不大，在加入十字模型进行前景提取后，双层椭圆模型的定位误差下降并不多，但仍明显优于椭圆模型。而马鞍模型在消除伪目标后，剩余亮度较高的点都在实际目标附近，求平均后定位效果较好，这说明基于十字模型的前景提取法对于其他模型也同样适用。

5.2 室外大区域环境下定位性能比较

图 7(a)、图 7(c)、图 7(e)分别是室外大区域环境中目标在（4.5 m，4.5 m）位置时分别用椭圆模型、马鞍模型、双层椭圆模型得到的成像图。图 7(b)、图7 (d)、图7 (f)是各模型加了十字模型提取前景后得到的定位图。相较于前面室外小区域，在室外大区域用20个节点覆盖100 m2的范围，覆盖的范围更大，相应链路密度也变低。然而与传统的有设备目标定位不同，RTI技术并不是通过目标与收发节点之间直接测量信号强度或时延等信息，再通过三边或三角计算获得目标位置，而是通过目标对电磁场的影响反演出目标位置，其定位精度并不与测量链路的多少成正比，相反过多的无效链路反而会影响成像质量和定位结果，特别是可能提高伪目标出现概率。事实上，RTI定位方法仅需利用几条通过目标的链路就可以实现成像定位，因此节点数目变化和定位区域的扩大并不会直接影响定位精度。目前RTI之所以需要较多的测量节点，是为了避免出现定位盲区，而不是提高定位精度。对于本实验来说，尽管定位区域有100 m2，但20个节点组成的网络可以提供 380条无线链路，链路密度仍可达到3.8条/ m2，因而出现定位盲区的概率并不高，并不会因为定位区域的扩大而影响RTI的实现。因此，与室外小区域环境的定位结果类似，相较于马鞍模型和椭圆模型，使用双层椭圆模型后RTI成像的背景更为清晰，伪目标也更少，而且通过十字模型进行前景提取后都能比较完美地滤去背景噪点。

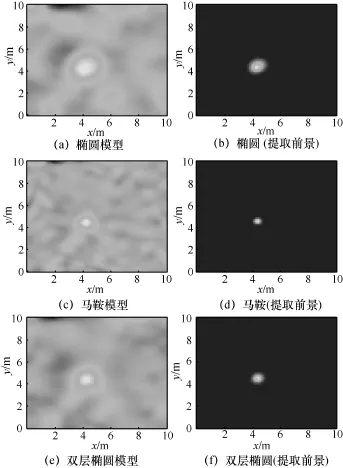
图7 室外大区域环境下3种模型的成像图比较

与之相应，表2也给出了类似的统计结果。同样地，由于在定位过程中，椭圆模型和马鞍模型都存在因为伪目标亮度高于目标而出现定位失败的情况，为公平起见，表2中的数据同样分别给出了椭圆模型和马鞍模型全部数据的统计结果和除去定位失败情形后的统计结果。从表2可以看出，尽管定位区域扩大了，但定位精度并没有明显下降，尤其是在采用十字模型前景提取法后，定位精度与室外小区域情况下十分接近。

5.3 环境下定位性能比较

图 8(a)、图 8(c)、图 8(e)分别是室内环境中目标在（1 m,2 m）位置时分别用椭圆模型、马鞍模型、双层椭圆模型得到的成像图。图8(b)、图8(d)、图 8(f)是各模型加了十字模型提取前景后得到的定位结果图。由于室内环境下3种模型都会出现伪目标亮度比真实目标高的情况，因此统计时不再去除这种情况。

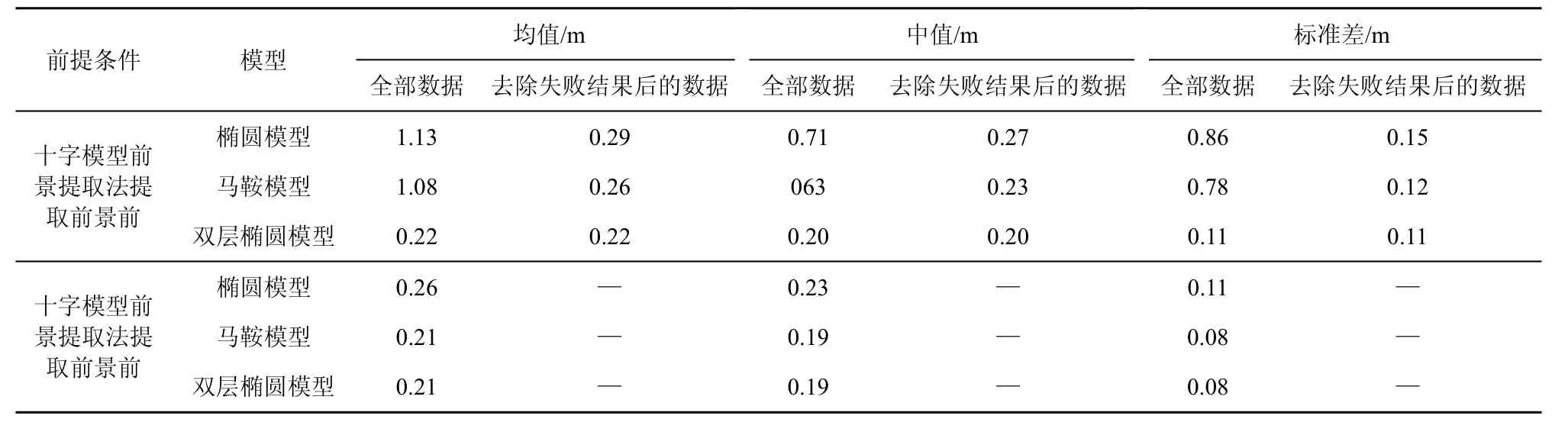
表2 室外大区域环境下各模型定位误差统计结果

图8 室内环境下3种模型的成像图比较

从图8可以发现，在室内定位情况下，由于墙壁、玻璃的反射、散射等因素，RSS测量值的波动更加剧烈，成像图上背景也相较于室外更为复杂。因此，在未进行前景提取时，一些伪目标的亮度值会明显高于真实目标的亮度，造成目标位置误判，定位精度不高。如表3所示，此时椭圆模型和马鞍模型的平均定位误差都超过0.8 m，双层椭圆模型的定位性能尽管是3种模型中最好的，但平均误差依然超过0.6 m。而且这时所有三种模型定位结果的标准差都很大，这意味着在室内环境下定位稳定性较低。然而如图8(b)、图8 (d)、图8 (f)所示，采用十字模型进行前景提取后，可以有效地消除背景噪点及伪目标的影响，此时3种模型的平均定位误差明显下降，并且此时的标准差也下降到0.25 m以下。这意味着采用本文提出的十字模型前景提取法后不仅定位精度提高，而且定位稳定性也明显提升。

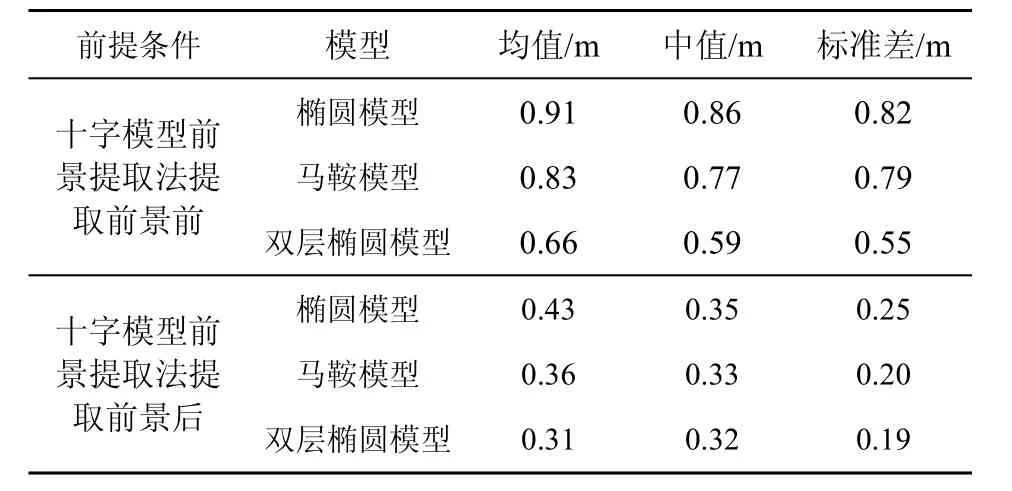
表3 室内环境下各模型定位误差统计结果

6 结束语

本文针对现有RTI方法中权重模型的不足，提出的基于菲涅耳衍射理论的双层椭圆权重模型。通过对第一菲涅耳区和最小菲涅耳区内的像素点赋予不同权重，以及对距离收发节点远近不同的像素点赋予不同的权重来提高RTI的成像质量和定位性能。同时，通过十字模型对定位图像进行前景提取，有效克服了伪目标影响，提高了定位精度。室内外不同环境下的实验结果表明，该方法的成像质量和定位精度都要优于现有RTI方法。下一步工作将考虑将本文方法推广到多目标DFL中。