基于贝叶斯算法的中文垃圾邮件过滤系统研究

刘浩然，丁攀，郭长江，常金凤，崔静闯

（1. 燕山大学信息科学与工程学院，河北 秦皇岛 066004； 2. 河北省特种光纤与光纤传感重点实验室，河北 秦皇岛 066004；3. 燕山大学里仁学院，河北 秦皇岛 066004）

1 引言

随着信息技术和网络技术的不断发展，垃圾邮件在互联网上急速蔓延，其内容往往是广告或虚假信息，甚至是电脑病毒等不良信息。大量垃圾邮件的传播不仅给人们工作和生活带来极大的困扰，而且还造成了网络资源的浪费。

目前垃圾邮件过滤技术主要可分3类：黑白名单过滤、基于规则过滤和基于内容统计过滤。其中，基于内容统计过滤常见算法有朴素贝叶斯（NB,naive Bayesian）、支持向量机（SVM, support vector machine）、最近邻（KNN, k-nearest neighbor）等。

早期研究对垃圾邮件过滤奠定了良好基础。1998年Sahami首次将朴素贝叶斯算法应用到垃圾邮件过滤中[1]。2000年Androutsopoulos等[2]证明朴素贝叶斯算法明显优于基于关键字的过滤器方法。2002年Drucker等[3]将SVM用于垃圾邮件过滤中，并证明SVM算法优于贝叶斯和其他基于规则过滤的方法。2005年Healy等使用k-NN算法过滤垃圾邮件，2008年Wu等使用贝叶斯学习提取关键词的方法过滤垃圾邮件，且都通过实验证明了各自算法的有效性[4]。

近年来，研究者在对传统算法做改进的同时，其他算法也被应用，如lazy learning、C5.0、J48和随机森林等[5]。文献[6]将粗糙集理论应用于垃圾邮件过滤，并证明其性能优于当下其他方法。文献[7]将特征加权应用于垃圾邮件过滤，并在计算概率的过程中定义了2个风险因素以提升过滤准确率。文献[8]采用支持向量机和 k-mean聚类混合算法来增强SVM，提高了垃圾邮件分类的准确率。

不同分类模型适用于不同的文本特征，无论是根据特征寻求分类模型改进还是直接对模型改进都可提升过滤性能。文献[9]采用基于信息熵和增量学习的方法分析各种特征如何影响基于RBF（radial basis function）的SVM垃圾邮件分类器的性能，从而通过提取有意义的特征来提高垃圾邮件过滤性能；类似地，文献[10]采用CN2-SD（CN2-subgroup discovery）算法对每个领域提取语义特征，分别建立适合于每个领域的分类器来提高垃圾邮件过滤性能，二者都根据特征属性建立模型。文献[11]提出的TSVM-NB（twin support vector machine-naive Bayesian）算法先用NB对样本初次训练后用SVM构造最优分类超平面，再用NB训练生成分类模型；文献[12]表明基于生成分类模型的 RNN对数据分布的变化更具有顽健性，证明了生成模型优于判别模型，二者都对分类模型做分析和改进。文献[13]对SVM、gradient boosting、神经网络和随机森林分类器进行性能比较，实验结果显示，不同分类模型对不同特征集的分类性能具有差异性。

垃圾邮件过滤算法各有优缺点，有的提高了过滤速度却牺牲了准确率，有的则牺牲过滤速度来提高准确率。文献[14]对NB、SVM、J48、KNN、NB-M（multinomial naive Bayes）、NB-MU（updatable naive Bayes）、NB-C（cost sensitive naive Bayes）和随机森林8种算法进行对比，结果表明NB与SVM的过滤性能相当，在速度和准确率上表现更好；随机森林在建模和过滤上速度缓慢，但准确率高；其余算法速度快但准确率低。从正确率、准确率、查全率和F1-Measure这4项过滤性能来看，文献[15]表明其提出的语义长短期记忆网络(SLSTM, semantic long short term memory)的过滤性能最佳，NB、SVM、随机森林和人工神经网络表现相当，但明显优于KNN。

与其他方法相比，贝叶斯方法具有数学基础坚实、分类效率稳定、模型清晰等优点，但也存在属性之间的独立性假设不成立的缺点[16]。通过放松条件独立性的假设可做出改进，如结构扩展、局部学习、特征选择、特征加权等[17]。为提高垃圾邮件过滤效果，本文首先提出一种基于中心词扩展的TF-IDF特征提取算法，以增加特征节点的表达能力，达到特征降维；其次，采用3层的贝叶斯网络结构模型，以增加特征多样性，避免分类模型中特征局限的缺陷；再次，在训练3层的贝叶斯网络结构模型时，提出一种 GWO_GA结构学习算法，旨在放松属性间的条件独立性假设，使得数据与模型结构更好地拟合；最后，通过实验验证基于中心词扩展的 TF-IDF特征提取及GWO_GA结构学习的 3层贝叶斯算法的可行性和有效性。

2 基于中心词扩展的TF-IDF特征提取算法

针对特征提取时因中文文本稀疏性导致特征维度过高的问题，本文提出一种基于中心词扩展的TF-IDF特征提取算法，选择高频特征词作为中心词，设置权重阈值向其周边做特征扩展，可增加网络中特征节点的表达能力，实现特征降维。

2.1 中心词扩展

向量空间模型(VSM, vector space model)是一种不考虑特征词出现的位置、次序及上下文关系的词袋模型，将特征词在文本中出现的频率作为文本分类的依据[18]。

定义 1中心词扩展。设定某个单词作为中心词，以一定的方式搜寻文本中与其相关的词作为扩展词，并将这些词放在同一个词袋中，这种扩展词袋的方法叫做中心词扩展。

中心词扩展是为了增加词袋的表达能力，降低特征维度。凡包含在中心词词袋内的单词都可表示该中心词属性。假如以 word作为中心词，经过中心词扩展后，以word作中心词的词袋中就包含x1、x2、x3等单词，则只要x1、x2、x3等中至少一个单词出现，即认为word属性出现。如图1所示，若“苹果”“华为”“三星”等中至少一词出现，就可表征“手机”属性。

在贝叶斯网络结构中，以一个中心词词袋作为特征节点，当越来越多的单词被视为与中心词同属性而加入词袋中时，该特征节点可以表示的特征词增多，表达能力自然得以提升。

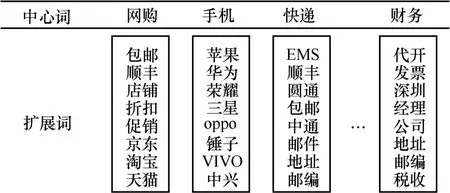
图1 中心词扩展模型

2.2 TF-IDF特征提取

经过文本特征统计发现，在所有词性中，对文本分类贡献最大的是名词，选用名词作为特征词最具优势。然而，不同名词对文本分类的贡献不尽相同，因此，名词特征需要做加权处理。

特征加权是根据某种标准对特征子集内的特征词赋予一定的权重，特征词对分类越有利，被赋予的权值越大。特征加权使同类文本的空间结构更紧凑，异类文本的空间结构更稀疏[19]，这有助于改善文本稀疏性带来的特征高维问题。

TF-IDF是目前应用较多的一种特征加权算法，由词频(TF, term frequency)和逆文档频(IDF, inverse document frequency)两部分组成，用W表示特征词x的权重，可计算TF-IDF权重如式(1)所示。

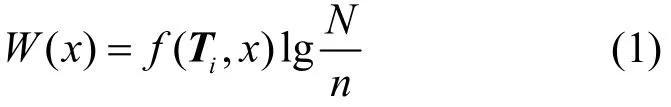
其中，N为文本集T={T1,T2,…,Tn}中的文本总数，n为文本集中包含特征词x的文档数量，Ti表示文本集中第i个文本，f(Ti,x)表示单词x在文本Ti中出现的频率。

2.3 基于中心词扩展的TF-IDF特征提取

为了增强网络结构中特征节点的表达能力，降低特征维度，本文提出基于中心词扩展的 TF-IDF特征提取算法，选择高频特征词作为中心词，设置权重阈值向其周边做特征扩展。

采用词关联方式为特征做中心词扩展，以某个词作为中心词向外做词意扩展，将与之相关联的特征词放在同一词袋中作为一个特征集。文本在分词和去停用词的文本预处理后，遍历所有文本，找出权值高于阈值g（权值的平均值）的词作为关联词，加入到中心词词袋中扩充词袋词量。

算法1是基于中心词扩展的TF-IDF特征提取算法。首先，统计文本集T中所有单词的词频f(T,x)，用词频最高的前m（高于词频数学期望值的单词量）个单词组成中心词集C= {C1,C2, …,Cm}；其次，统计每一个文本Ti中单词x的词频f(Ti, x)，并统计含有单词x的文本在文本集T中的数量n；然后，通过式(1)计算每个单词的权重W(x)；最后，遍历所有文本，若第j个中心词Cj在文本Ti中出现，则将文本Ti中权值大于阈值g的所有单词加入到该中心词词袋中，作为特征集X={X1,X2, … ,Xm}中第j个特征子集Xj的特征词

采用基于中心词扩展的TF-IDF算法提取特征，使得特征节点具有更大的多样性，达到一词多意的效果，在增加贝叶斯网络特征节点表达能力的同时特征词也得以降维。

余弦相似度用向量空间中2个向量夹角的余弦值来衡量2个文本间差异，计算测试文本特征A与贝叶斯网络中第j个特征子集Xj的余弦相似度，如式(2)所示。

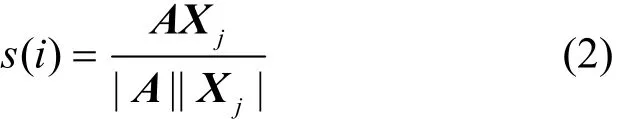
在提取到测试文本特征并进行归一化处理后，使用余弦相似度s(i)作为测试文本特征与类特征相似度量方式，比较所有相似值，选用相似值最大的特征节点来表征测试文本。

3 3层贝叶斯网络分类算法

针对分类模型存在特征局限的缺陷，本文采用3层贝叶斯网络结构模型建立分类器。3层贝叶斯网络模型的本质是对特征词层次式的组织，在类与特征节点之间增加细分类层，旨在提高特征覆盖面，改善文本特征局限的缺陷。提出一种GWO_GA结构学习算法，混合灰狼算法的头狼引导和遗传算法的选择、交叉及变异算子进行结构寻优，通过结构学习算法放松属性间的条件独立假设。

3.1 3层贝叶斯网络结构模型

定义 2 特征局限。假设中文邮件中包含有n种类型的垃圾邮件，由于某类邮件数量较多、特征词出现频次高和敏感词多等因素，在特征层选定特征词时，大量该类特征词被标记为垃圾邮件特征而其他类特征词未被标记，把这种特征过于偏向或局限于某类的现象称为特征局限。

从结构上分析，直接由类节点连接特征节点的结构模型容易导致特征局限，特征局限使得某些垃圾邮件的特征无法与类特征匹配，从而将垃圾邮件误判为正常邮件，这对多领域邮件过滤不利。针对分类模型特征局限的缺陷，本文采用3层贝叶斯网络结构模型以效弥补该缺陷，在类节点与特征节点中间加入一个细分类层，对特征词层次式的组织，让中文邮件类下存在更多细分类以保证每个细分类的特征都被覆盖，从而避免了特征局限的问题。

基于3层贝叶斯网络结构如图2所示，根据本文收集邮件的具体情况，将邮件大体分成3个细分类：广告类(ad)、工作类(work)、财务类(finance)。当然，根据邮件过滤需要，细分类数量可增多。

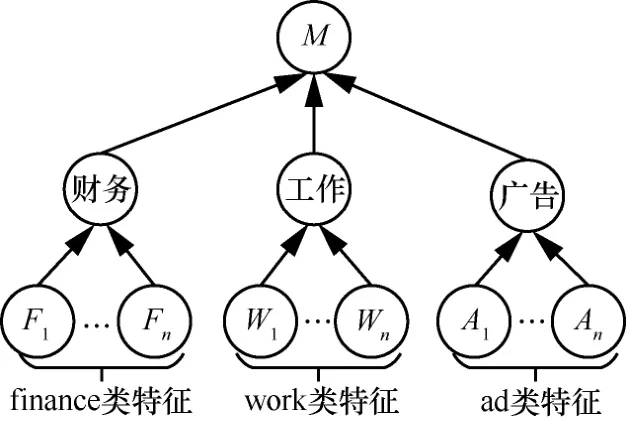
图2 3层贝叶斯网络结构模型

3.2 GWO_GA结构学习算法

贝叶斯分类算法需要通过适度放松其所需条件独立性假设的方法对其做出改进。本文根据3层贝叶斯网络模型的结构特点，结合垃圾邮件过滤的具体需求，提出一种混合灰狼和遗传的结构学习算法——GWO_GA算法，用以对分类器模型进行结构学习，并只对特征层到细分类层做结构学习训练。

3.2.1 遗传算法

遗传算法(GA, genetic algorithm)中包含3个核心算子——选择、交叉和变异，本文参考文献[20]中所采用的方法，用于对垃圾邮件过滤系统中的分类器筛选结构和增加结构的多样性，并使评分高的结构被留下，保证训练垃圾邮件分类器的迭代过程中出现更多的继承父代基因且优于父代的新结构，以获取全局最优的网络结构。

垃圾邮件分类器中，分类器结构为GA算法的种群个体，对分类器网络结构评分为GA算法的个体的适应度。

分类器结构选择。采用轮盘赌选择可提高选中次优结构的机会，增加分类器结构的多样性，避免陷入局部最优[20]。轮盘赌选择中，将对所有分类器网络结构的评分置于同一圆盘中，随机转动圆盘，停止后指针所指区域为所选结构。图3为轮盘赌选择操作，由于评分越高的结构在轮盘中所占面积越大，在分类器结构选择操作中，选到评分高的结构的可能大于评分低的结构，但评分低的结构仍有选中的机会，因此在评分高的结构得以保留的同时又增加了结构的多样性，避免搜索像 HC（hill climbing）算法那样陷入局部最优。

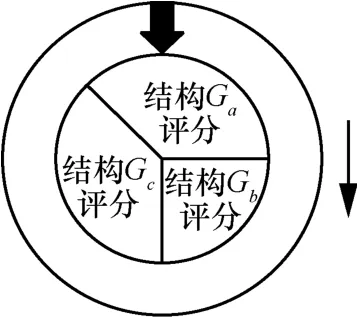
图3 轮盘赌选择操作

分类器结构交叉。采用行（列）间交换进行分类器结构的随机交换，2个父代网络结构的部分结构交换重组以产生新结构[20]。图4为行交换交叉操作，将2个父代网络结构Ga和Gb的同行进行交换（可一行交换，也可多行交换），如行a1—a4与行b1—b4交换。分类器网络结构在通过交叉操作后，结构不断更新，提高了分类器的搜索能力。

分类器结构变异。对分类器网络中细分类与特征间互信息值较大的边做加边操作，互信息值较小的边做减边操作[20]。依据细分类与特征间的互信息对结构向量中的边进行变动，由于细分类与特征间的互信息是表征2个节点存在因果关系的量度，在变异过程中，随机选择结构列进行变异操作，若选中边的节点间互信息值较高，则对该边做加边操作，反之则对该边做减边操作。

图4 行交换交叉操作

3.2.2 GWO_GA算法

在对垃圾邮件过滤分类器进行结构学习时，受灰狼优化算法(GWO, grey wolf optimizer)[21]中3只头狼引导种群更新位置的思想启发，迭代中，在分类器网络结构更新后，选出3个评分最高的结构，并将它们的交集作为下次迭代的初始结构。3个结构都存在各自的缺陷，需找出3个最优结构的共同列作为最终的分类器结构，即求交集。

算法2为GWO_GA结构学习算法，先通过计算分类器的细分类与特征节点间的互信息，来构建最大支撑树G0。给仅能表示节点间有无关系的无向图随机定向会降低搜索效率，故采用节点间轮流当父子节点做BIC评分，将评分高的作为分类网络中边的方向，以获取初始化结构G。获得初始化结构后，算法进入迭代寻优，搜索最优的分类器结构。

迭代中，首先通过随机加边、减边和转边的方式获得分类器的初始结构，并对其BIC评分。其次采用转盘赌选择，从初始结构中选出10个结构（依据为GWO算法的狼群数量）作为父代结构；每2个结构间进行交换交叉操作产生子代结构；对子代结构中互信息值大的进行加边操作，小的进行减边操作，并对新结构BIC评分。最后，对新结构中最优的前3个结构求交集，将3个最优结构的共同边作为下次迭代的初始结构。在满足迭代停止条件前，重复以上迭代过程，多次迭代直至搜索到最优结构，并将评分最优的结构作为最终分类器结构。

在垃圾邮件过滤系统中，使用GWO_GA算法训练分类器结构，通过对已标记的邮件数据进行结构学习，拟合出较贴合实际数据的分类器结构。

4 垃圾邮件过滤系统

本垃圾邮件过滤系统可分为特征提取和贝叶斯分类两大部分，其中，贝叶斯分类部分需经过结构学习、参数学习和推理3个过程，这是贝叶斯网络研究的一个完整过程。首先，通过结构学习建立拓扑网络；然后，通过参数学习为计算条件概率；最后，通过贝叶斯推理进行文本分类。

在使用以上算法完成特征提取、建立模型和结构学习后，在已知网络拓扑结构的情况下，用最大期望算法(EM, expectation maximization)[22]对节点进行参数学习，通过给定文本数据，学习整个贝叶斯网络的概率分布。用联合树推理算法[23]进行类别推理，将待测文本特征作为证据，去除与文本特征及类无关的所有节点后，求其属于某类的后验概率，即利用条件概率推出联合概率后，计算出最终类别的边缘概率。

图5为垃圾邮件过滤系统流程，在特征提取部分，经过文本分词和去除停用词等文本预处理后，采用基于中心词扩展的 TF-IDF特征提取算法对文本做特征提取，并将特征向量化。在贝叶斯网络部分，首先，使用GWO_GA结构学习算法训练3层贝叶斯网络结构模型，构建拓扑结构；其次，通过EM参数学习训练样本数据，计算节点的先验概率，并保存到条件概率表(CPT, conditional probability table)中；最后，在给出待测文本d提供证据的情况下，结合CPT采用联合树推理算法进行推理，使用垃圾邮件与正常邮件的概率比是否高于均值给出类别判定，并标定垃圾邮件。

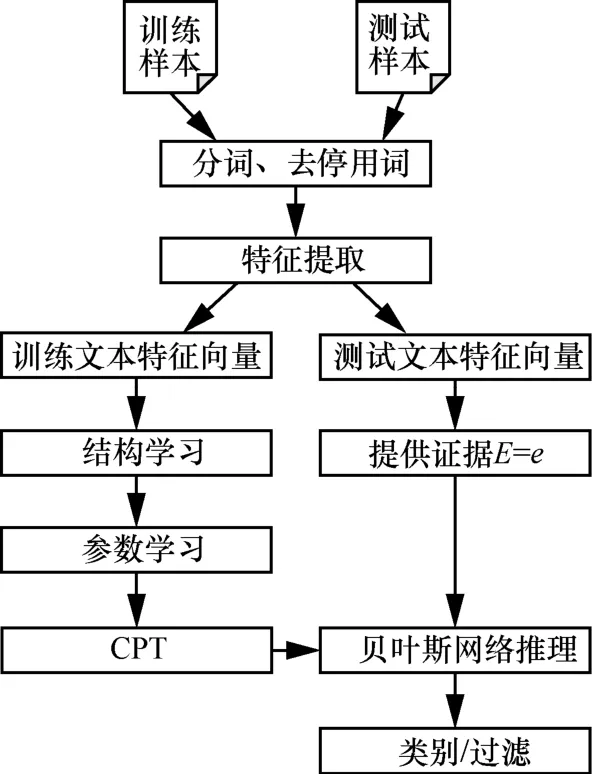
图5 垃圾邮件过滤系统流程

垃圾邮件过滤系统过滤流程可以分为如下5个步骤。

步骤1文本预处理。先使用NLPIR汉语分词系统对文本进行分词处理，将非名词单词以及英文词作为停用词去除，做去停用词处理。

步骤 2特征提取。依据本文提出的基于中心词扩展的 TF-IDF特征提取算法，对训练样本做特征提取，并将所提取特征向量化。

步骤3结构学习。手动建立本文提出的3层贝叶斯网络结构模型，同时，使用本文提出的GWO_GA算法对该模型进行结构训练。

步骤4参数学习。使用EM参数学习算法对样本数据进行参数学习，计算节点发生的先验概率，并保存到CPT中。

步骤 5推理。将待测文本与特征集做相似度量，选择相似度最高的特征节点作为证据，采用联合树推理算法进行推理，计算出给定证据是否为垃圾邮件类的后验概率，并对邮件进行类别标定。

5 实验

本文实验部分首先对本文算法和原始GA算法进行收敛性分析，证明本文算法的可行性。其次，对本文算法与朴素贝叶斯算法的性能进行比较，以证明3层结构模型的可行性和有效性。然后，将本文算法与使用经典HC算法、GA算法和本实验室已有的SHC（simplify hill climbing）算法[24]贝叶斯网络结构训练后的中文垃圾邮件过滤效果同时进行性能对比，以证明本文算法对经典算法改进的有效性和优越性。最后，为使本文算法更具有普遍意义，实验还增加了TREC公共垃圾邮件语料库中文版 trec06c数据集下，当前新的过滤算法与本文算法的对比结果。

5.1 实验数据

在互联网科技迅速更新的环境下，网络用语也在不断更新。由于网络上大多数开源的邮件数据库相对老旧，大多数邮件不符合当下邮件过滤的实际需求，故本文选择自己收集邮件。根据笔者个人工作环境，本文收集了3 000封邮件文本作为数据来源，其中包括广告、工作和财务的3类邮件，而这3类邮件文本中，正例文本(垃圾邮件)占比 60%，反例文本(正常邮件)占比 40%。同时，为使结果更具普遍意义，实验还使用2006年TREC公共垃圾邮件语料库中文版 trec06c作为实验样本，选用trec06c前10 000封邮件作数据来源，其中，垃圾邮件6 631封，正常邮件3 369封。

在朴素贝叶斯邮件过滤中，没有将邮件文本分为广告、工作和财务的3类邮件，而是只分正例文本和反例文本。本文收集的3 000封邮件文本中，2 000封为训练样本，其余1 000封为待测样本。

在3层贝叶斯网络邮件过滤系统中，则将邮件文本分为广告、工作和财务3类邮件，每类邮件分正例文本和反例文本。同样，3 000封邮件文本中，2 000封为训练样本，其余1 000封为待测样本。

5.2 评价指标

收敛(收敛性)是指函数或数列是否存在极限，设数列{Li}，若存在常数a，对于给定任意小的正数b，总存在正整数I，使得i＞I时，|Li-a| ＜b恒成立，则称数列{Li}收敛。

本文把GWO_GA算法和原始GA算法迭代过程中对最优结构的BIC评分作为判断依据，将每次得到的评分放在同一数列中，并通过绘制数列曲线图来判断算法的迭代是否收敛。由于BIC评分结果为负值，为方便绘图，对评分取绝对值，因此，绘制数列曲线图中评分值越小，实际评分越高。

使用正确率(accuracy)、准确率(precision)、查全率(recall)和 F1-Measure作为垃圾邮件过滤的性能评价指标。设判断正确的邮件量记为at，判断错误的邮件量记为af，全部测试邮件量记为at+af。将垃圾邮件判定为垃圾邮件的总量记为tp，将正常邮件判定为垃圾邮件的总量记为fp，将垃圾邮件判定为正常邮件的总量记为fn。

正确率A表示为

准确率P表示为

查全率R表示为

F1-Measure表示为

5.3 实验结果及分析

如5.2小节所述，曲线评分值越小，实际评分越高。图6中，随着迭代次数的不断增加，本文GWO_GA算法和原始GA算法的BIC评分在10次以内曲线急剧下降，表示实际评分值急剧上升，20次到30次以内优势减缓，而后则维持在一定值上下小幅度波动。由此可证明，本文算法具有收敛性，且本文算法的收敛效果优于原始GA算法，说明本文算法具有可行性。

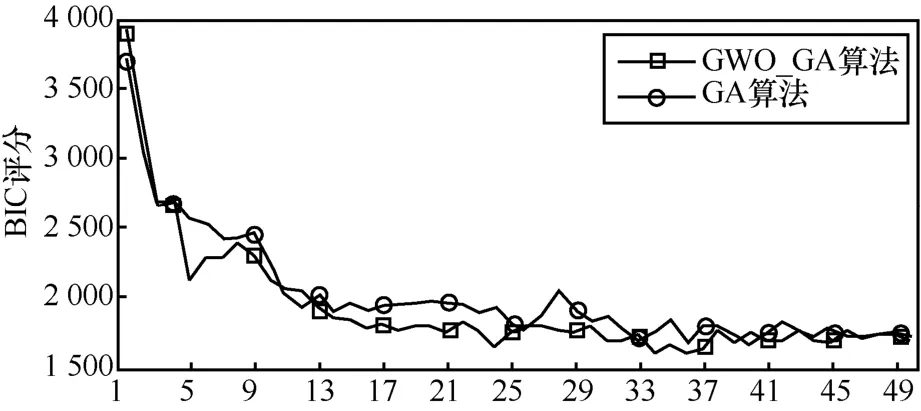
图6 BIC评分曲线

图7中，随着训练样本量的增多，朴素贝叶斯算法的正确率先是基本维持在60%左右，后有所下降；而本文算法的正确率则稳定在75%左右。

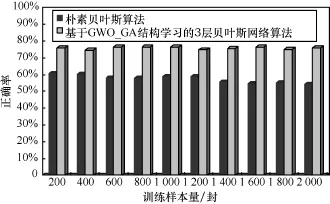
图7 分类正确率对比

对朴素贝叶斯算法而言，由于训练文本的不断增加，提取到的特征基本稳定。而由于中文文本特征具有稀疏性，文本特征具有一定噪声，样本基数不断上升，导致先验概率变小，故分类效果出现稳定到下滑的变化，当测试文本中有用的特征达到饱和时，训练样本的增多就成为负担，反而导致先验概率变小，分类效果下降。然而，对本文算法而言，3层结构使得特征覆盖面增大，特征多样性增加，在细分类与特征节点的关系确定的情况下，尽管训练文本在不断增加，分类效果也保持稳定。由此可证明，本文算法比朴素贝叶斯算法具有更强的顽健性，3层结构模型具有可行性和有效性。

图8为4种算法在不同数据集下的正确率、准确率、查全率和F1-Measure的表现。从图8中可以看出本文GWO_GA算法和原始GA算法在正确率、准确率、查全率和F1-Measure这4个分类指标上都比较稳定，而经典HC算法和SHC算法波动较大，尤其是在查全率上，遗传算法稳定性优于HC算法。随着训练样本数据量的上升，本文算法整体上呈现上升的趋势，说明随着训练学习的增加，分类性能也在上升；同时，本文算法各项性能都明显优于其他算法，可见本文算法的性能优越性。

正确率高说明将正常邮件和垃圾邮件判定正确的数量多，准确率高说明将正常邮件判定为垃圾邮件的数量少，查全率高说明将垃圾邮件判定为正常邮件的数量少，F1-Measure值则是综合表现。从各项数值来看，本文算法相较于其他算法分类性能提升近10%。而所有算法的查全率高说明算法对垃圾邮件的特征把握得较好，原因可能是选取邮件样本中，正例文本偏多。

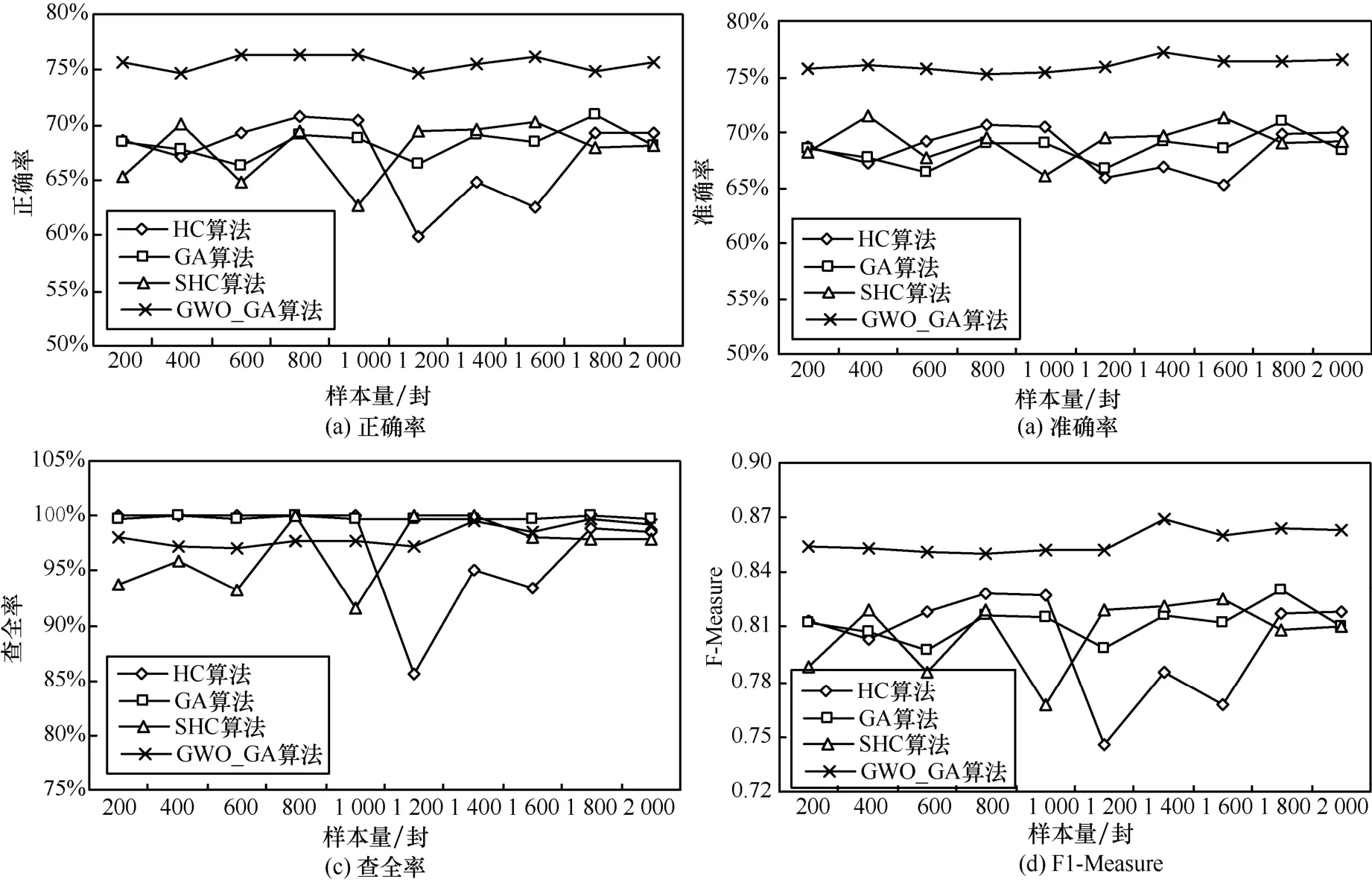
图8 4种算法分类性能指标

表1为使用2006年TREC公共垃圾邮件语料库中文版 trec06c作为实验样本的情况下本文算法与当前新算法分类性能的比较，从表1可看出，用RBF-SVM 算法表示文本向量的加权分布特征算法，PTw2v算法[25]对垃圾邮件有较优的分类性能，相比之下，本文算法与逐层添加注释语义特征提取的C4.5算法[26]相当，而优于SHC算法。

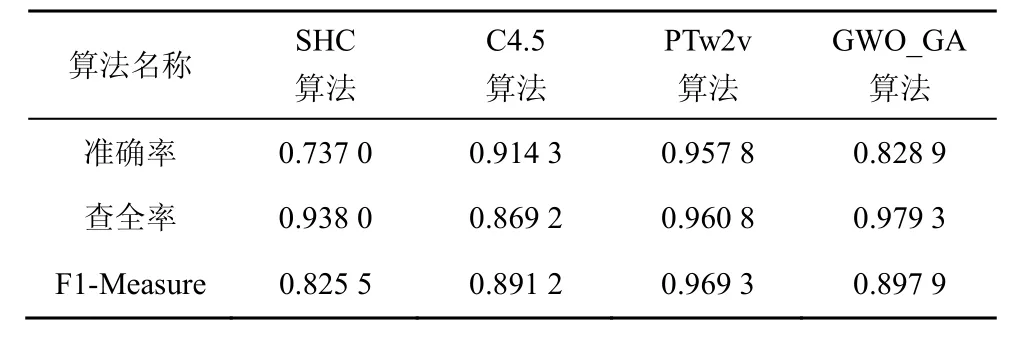
表1 trec06c语料库4种算法分类性能对比

使用公开垃圾邮件语料库实验的分类性能比自己收集的实验数据集优，说明该公开语料库更适合进行实验。与当前新的过滤算法相比，本文算法在查全率上凸显出优势，说明层次式特征细化类别可降低误判率。本文算法在准确率上略显不足，原因可能是本文在特征选择上将高频词作为中心词，会将某些对特征不明显的词当成特征并扩展，将普通词作为特征会使正常邮件的特征与垃圾邮件特征关联性增加，从而使正常邮件误判为垃圾邮件，降低准确率，下一步将针对此问题做出改进。

3层结构模型这种层次式特征在单一类别垃圾邮件过滤中并不能使分类性能提升，但对于多领域分类而言，层次式特征的3层结构模型降低了误判率。真正对分类性能有提升作用的是新的分类器，新的结构学习算法对分类器结构进行了优化，相比根据专家知识做出的属性间条件独立性假设，GWO_GA算法训练的贝叶斯网络结构对数据拟合得更好。

6 结束语

本文基于GWO_GA结构学习算法和3层贝叶斯网络模型建立了中文垃圾邮件过滤的系统，通过GWO算法的头狼引领和GA算法选择、交叉和变异算子的混合实现了网络结构的遗传迭代寻优，使得数据与结构充分拟合。而基于中心词扩展的TF-IDF算法则极大降低特征维度，直接增加了特征节点的表达能力。在贝叶斯网络的3层结构模型改善特征覆盖面局限缺陷的同时，使用GWO_GA结构学习算法放松模型结构属性之间的独立性假设。使得整个垃圾邮件过滤系统具有良好的过滤性能，提高了垃圾邮件过滤的效果。