改进蜂群算法求解大规模着色瓶颈旅行商问题
董文永,董学士,王豫峰
(武汉大学计算机学院,湖北 武汉 430072)
1 引言
着色旅行商问题(CTSP,colored traveling salesman problem)[1-4]可应用于具有部分重合工作区的多机器工程系统(MES,multi-machine engineering system)的规划问题。瓶颈旅行商问题(BTSP,bottleneck traveling salesman problem)[5-9]是 TSP 问题的一种变化模型,其目标是最小化旅行回路的最大边,可应用于工作流的规划等领域。虽然 CTSP与BTSP可处理一些实际问题,但不能用于建模有部分重合区域的易于人员与车辆调配的路线优化问题,因此,本文探讨一种分析模型CBTSP,可建模具有合作与单独任务的人员与车辆调配的路线规划问题,该问题的目标函数是最小化所有旅行路线的最大边[10]。在智能交通、多任务协作等领域,一些实际问题都可用 CBTSP来建模,所构建问题模型的尺度往往趋向于大规模,即对应城市数量在几千或以上,因此,研究大规模的 CBTSP问题及其求解算法有一定的实际意义。此外,CBTSP在一定条件下,可转化为CTSP、BTSP和TSP等组合优化问题,因此探索可行的 CBTSP求解算法可对其他相关优化问题的研究有借鉴意义。相关文献的研究已证实,蜂群算法求解TSP等组合优化问题表现出较好的性能,基于此,本文将一种改进的蜂群算法应用于求解大规模CBTSP问题。
CTSP是近年刚被提出的问题,目前在这方面的研究文献较少。东南大学李俊等[1-2]将遗传算法(GA)贪心遗传算法(GAG)、爬山法遗传算法(HCGA)与模拟退火遗传算法(SAGA)应用在求解小规模的CTSP问题,即该问题的城市数量小于或等于101。之后,文献[3]应用一种可变的临近搜索算法求解CTSP,进一步提高了已有算法求解该问题的性能;文献[4]给出了一种基于多任务学习的蚁群算法求解CTSP,并将问题所对应的城市数目拓展到1 002。BTSP问题的部分研究工作包括:相邻信息序列的排序可以映射成为 BTSP,文献[5]采用一种近似算法求解该问题;文献[6]对不对称BTSP问题的算法、复杂性和经验分析进行了研究;Ahmed应用混合遗传算法优化BTSP问题,并通过实验证实该算法的有效性[7];此外,文献[8-9]也对 BTSP进行了相关的研究。文献[10]给出了着色瓶颈旅行商问题,并提出了一种混合算法求解该问题,其中 CBTSP问题的规模(即对应的城市数量)小于或等于2 361。近年来,大规模优化的部分相关工作包括:Cheng等给出了一种可用于大规模优化的竞争种群优化器,引入一种成对的竞争机制,求解过程中失去竞争力的粒子将进行更新[11];针对大规模市内路网的信号划分优化,Ye等设计了一种分层模型预测控制方法[12];求解大规模黑箱优化问题,Omidvar等设计了一种快速和多精确差分分组方法[13];Zhang等提出了一种决策变量聚类的演化算法求解大规模许多目标优化问题[14];Hu等针对大规模优化,给出了一种快速相依性识别的协同演化算法求解该问题[15]。
本文探讨了一种问题模型CBTSP,该模型可建模含有协作与单独任务的人员与车辆调配的路线规划和优化问题,并将改进蜂群算法应用在求解大规模CBTSP问题,该算法首先利用m-tour编码方法生成问题的可行解,然后运用产生邻近解的方法对蜂群算法求解该问题做进一步的优化,从而得到问题的最优解。通过实验表明,IABC算法求解大规模CBTSP是有效的,该算法的求解质量优于对比算法。
2 着色瓶颈旅行商问题
2.1 CBTSP问题
CBTSP问题[10]含有m个旅行者和n个城市,其中m,n∈Z={1,2,3,…},m<n。CBTSP可被定义为一个完全图G(V,E),V={0,1,2,…,n-1}表示城市集,每个边edge (i,j)∈E,i≠j。城市集V被分成m+1个非空集,包括m个独享城市集Vi,∀i∈Zm={1,2,3,…,m}表示只有旅行者i能访问,以及一个共享城市集U,可被所有的旅行者访问。定点di表示站点,是旅行者i的起始点。在CBTSP中,变量xijk(i≠j,i,j∈V,k∈Zm)表示第k个旅行者是否经过城市i到j。
CBTSP的目标函数表达式为
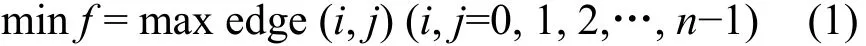
式(1)表示最小化整个旅行回路的最大边。
CBTSP问题的限制条件为[10]
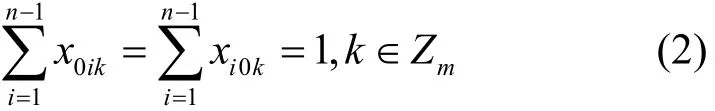
式(2)为旅行者开始和终止于站点。
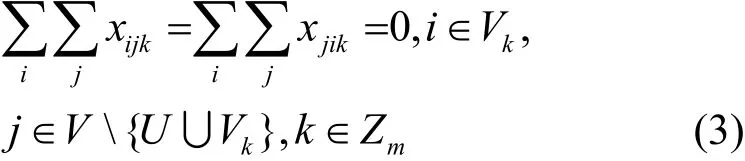
式(3)表示独享城市只能被指定的旅行者访问,其他旅行者无权访问。
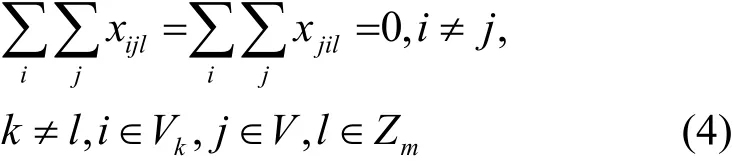
式(4)为旅行者l(≠k)不是开始和结束于第k个城市集。
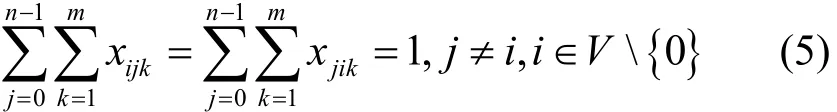
式(5)表示除站点外其他城市只能被访问一次。
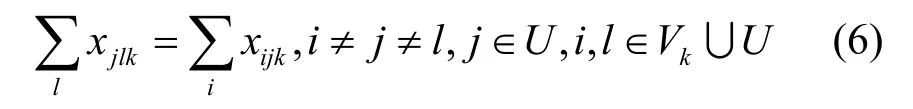
式(6)为所有旅行者同时访问和退出U。
2.2 CBTSP相关理论
CBTSP是非确定性多项式(NP, non-deterministic polynomial)难问题[1]:根据已知文献,CTSP是NP难问题,而CBTSP通过改变目标函数,可以转化为 CTSP,改变目标函数不会引起其复杂度的变化,因此CBTSP也是NP难问题。此外,CBTSP可以在一定条件下,即共享数据集为空集时,转化为多个单一的BTSP问题,因为BTSP属于NP难问题,而该形变操作不会引起模型时间复杂度变化,所以CBTSP属于NP难问题。
2.3 CBTSP与CTSP及其BTSP
CBTSP与CTSP的异同点如下。它们都有共享城市集和独享城市集,具有相同的限制条件和访问规则,每个城市只能被访问一次。但是它们有不同的目标函数,CBTSP的目标函数是使得所有哈密尔顿回路的最大的边最小化,CTSP的目标函数是使所有旅行回路的总的旅行长度最小。
CBTSP与BTSP的异同点如下。它们具有相同的目标函数,都是 TSP问题的变化模型。但是CBTSP有多个旅行者,可建模含多个旅行者多任务的优化问题,而BTSP只能建模单个旅行者单个任务的问题,它们有不同的限制条件和访问规则。
3 改进蜂群算法求解CBTSP问题
3.1 人工蜂群算法
人工蜂群算法(ABC,artificial bee colony)[16-19]是一种较新的群体智能算法,该算法模拟蜂群觅食的机制,蜂群可分为3类: 采蜜蜂、观察蜂和侦察蜂。优化问题的一个解由一个食物源的位置来表示,每个食物源的花蜜量表示对应解的适应度值,种群的大小为采蜜蜂和观察蜂的数量。
蜂群算法求解问题的具体步骤如下。
首先,随机产生一个初始的种群P,内含Np个解D维的决策变量Xi={xi,1,xi,2,…,xi,D},Xi由下界Xmin与上界Xmax定义。
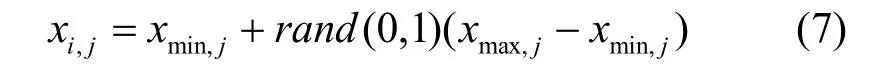
其中,i=1,2,…,Np,j=1,2,…,D。
蜂群算法中,一个采蜜蜂使用式(8)从前一个候选解Xi产生一个候选解Vi。
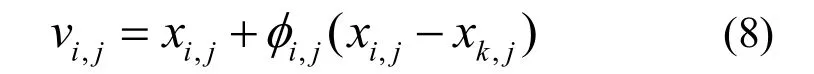
其中,k∈{1,2,…,Np}和j∈{1,2,…,D}是随机选择指数,k≠i,φij表示在[-1, 1]的随机数。
与采蜜蜂不同,观察蜂使用如式(9)的概率值pi选择一个位置访问来求解问题。
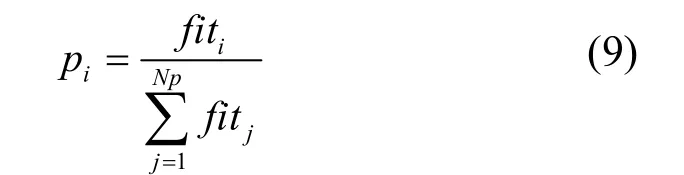
其中,fiti表示第i个解的适应度值。在该过程中,采蜜蜂与观察蜂可交换信息。
在观察蜂选择一个解之后,观察蜂运用式(8)产生一个新解,贪心选择应用于新的解和以前的解,采蜜蜂也是如此。当解在预先设定的循环不能被改进和优化时,此解将被舍弃,然后,对应的采蜜蜂变成侦察蜂,侦察蜂再通过式(7)产生一个新解[16]。
3.2 改进蜂群算法
改进蜂群算法是一种蜂群算法与局部优化相结合的算法,通过优化方法使蜂群算法获得的解得到进一步提升,求解CBTSP的具体介绍如下。
3.2.1 编码方案
本文采用的m-tour编码[20]方案用一组m个旅行者来表示 CBTSP问题的一个解。例如,如图 1所示,有一个11个城市3个旅行者的CBTSP问题,城市1和城市2属于旅行者1的独享城市,城市3和城市4是旅行者城市2的独享城市,城市5和城市6属于旅行者3的独享城市,城市7~城市11为3个旅行者的共享城市。用 m-tour编码方法表示CBTSP问题的一个解(不包括起始点):旅行者 1的访问顺序为(1, 2, 9, 10),旅行者2的访问序列为(3, 4, 11),旅行者3的访问顺序为(5, 6, 7, 8)。
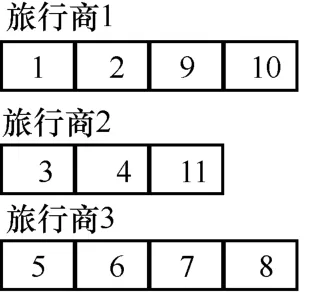
图1 表示CBTSP的m-tour编码方法
3.2.2 观察蜂选择蜜源的概率
采用二重锦标赛选择方法[20](binary tournament selection method)来选择观察蜂的一个蜜源。Pcopy位于预先定义的初始值Pmincopy和预先定义的最终值Pmaxcopy之间。Pcopy定义为
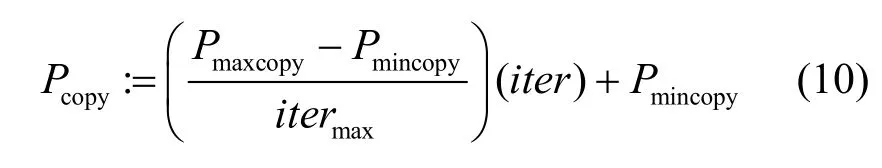
如果在一个设定的次数limitnoimp之后,采蜜蜂的解仍然没有得到改善,采蜜蜂及其蜜源将被放弃,采蜜蜂变成侦察蜂。通过随机产生一个解与侦察蜂相联系,侦察蜂可以再次变成采蜜蜂,侦察蜂的解通过相同的方式产生并设为初始解。
3.2.3 产生邻近解的优化方法
ABC可以使用局部优化进一步改善问题的解,在求解过程中,本文通过产生邻近解(GNS,generate neighboring solution)[20]进行优化,并在该过程中引入二个限制和优化条件。
GNS是对CBTSP解的访问序列进行部分删除和重插入操作,并在重插入时进行优化。例如,CBTSP的解S路径为 1—2—9—10—3—4—11—5—6—7—8,通过概率Pcopy将部分城市删除,并产生一个临近解S′,假设删除的城市为10、3、4、11,再将这些删除的城市重新插入到S′访问序列中。重新插入时有2个限制和优化条件,一个是独享城市只能插入到指定的旅行商的访问序列;共享城市可以插入到任意的序列,另一个是插入的城市位置使整个旅行回路的最大的边最小。重新插入之后,新解S′的访问序列可能为 1—2—9—11—4—3—10—5—6—7—8,如果S′优于S,就用S′替换S。

在算法1中,5)~11)表示将S访问序列的部分城市删除,未删除的城市赋值到S′,删除的城市赋值到未赋值的城市集。13) 将未赋值的城市集的城市c重插入S′中,该处有2个限制和优化条件:第一,独享城市只能插入到特定的旅行商访问序列;第二,重新插入城市的位置使整个旅行回路的最大的边最小。
3.2.4 改进蜂群算法求解CBTSP步骤
蜂群算法通过使用算法1对问题的解优化。算法2表示改进蜂群算法求解CBTSP的步骤[20]。

算法 2 中,6)~11)为采蜜蜂阶段,12)~18)为观察蜂阶段,19)~22)为侦察蜂阶段。IABC分别在采蜜蜂和观察蜂两个阶段调用算法 1(产生邻近解)对求解问题的解进行优化。
4 实验与分析
实验计算机的运行环境为 AMD AthlonTMII X4 3.01 GHz处理器和3.25 GB RAM。实验是用Java平台进行设计与开发。表1为CBTSP的实验数据,其中,1~14为小规模,15~27为中规模,28~49为大规模。
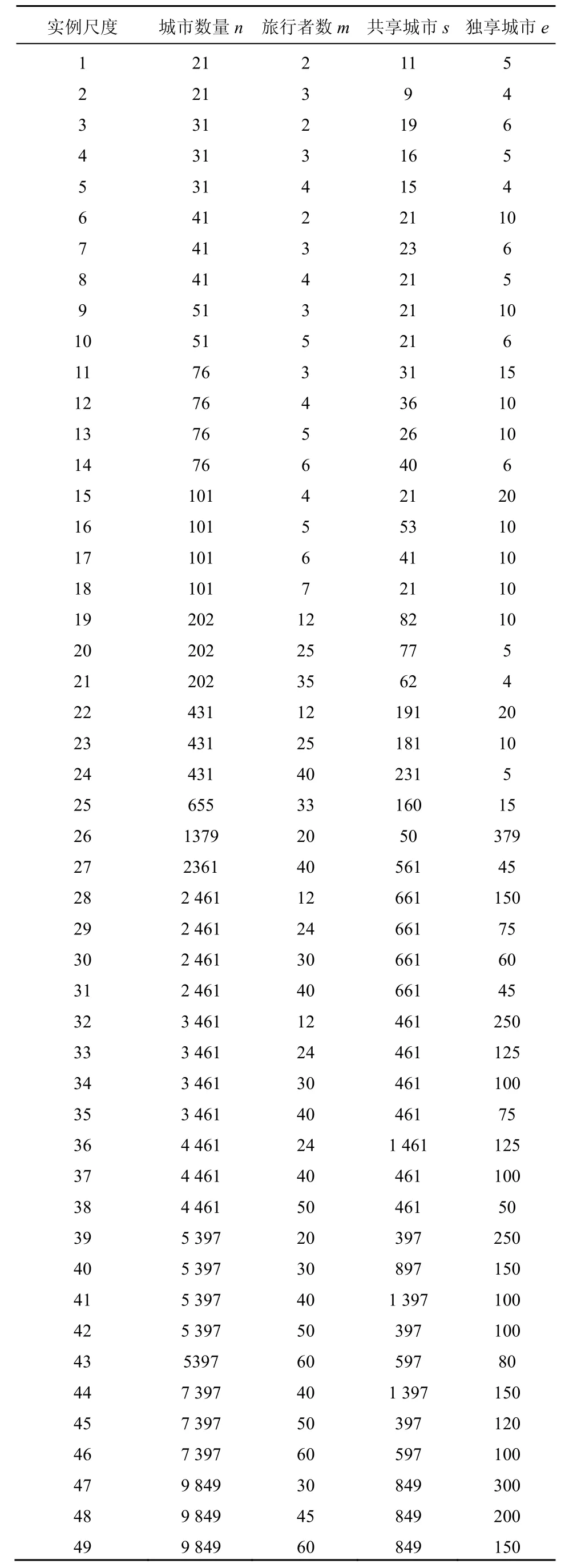
表1 CBTSP的实验数据
表1中有3种不同规模的CBTSP数据。n表示城市数量,其取值范围从21到9 849;m表示旅行者数,其取值范围从2到60;s表示共享城市的数量;e表示独有城市的数量。小规模和中规模的部分数据,即n的取值为21到101的数据,来自文献[1],大规模的数据由原始TSP数据制作而成,该TSPLIB 对称性TSP数据已在网上公开。
GA、GAG、HCGA与SAGA算法来自文献[1],根据相关实验该文献的算法参数设置可使算法获得较好的求解结果,参数设置具体如下:种群大小为30,交叉概率为0.7,变异概率为0.1。SAGA其他的参数设置如下:初始温度为 100,总的冷却时间为60,每个温度的步长为30,模拟系数0.9。蜂群算法和改进蜂群算法的参数为:limitnoimp设置为100,Pmincopy为0.2,Pmaxcopy为 0.9。图2~图6、表 2和表3中所有算法的最大未更新迭代次数均相同。
图 2(a)~图 2(d)分别为当n=31与m=4时,GAG、HCGA、SAGA与IABC求解CBTSP问题的运行界面。
图3(a)~图3(d)分别为当n=51和m=5时, HCGA、SAGA、ABC、IABC求解CBTSP。
图 4(a)~图 4(d)分别为当n=101与m=7时,GAG、HCGA、SAGA与IABC求解CBTSP问题。
图5(a)~图5(d)分别为n=431与m=40时,HCGA、SAGA、ABC与IABC求解该问题。实验详细情况如下:HCGA平均解是17 106.4,时间为0.2;SAGA平均解为16 873.4,时间为0.3;ABC平均解为14 477.3,时间为0.03;IABC平均解为10 318.6,时间为0.6。
图 6(a)~图 6(d)分别为当n=655与m=33时,GAG、HCGA、SAGA与IABC求解CBTSP问题。求解详细情况如下:GAG平均解为14 610.9,时间为0.3;HCGA平均解为14 231.0,时间为0.3;SAGA平均解为13 626.8,时间为0.6;IABC平均解 13 248.7,时间为0.9。从该实例数据可看出,IABC平均求解质量最优。
表2和表3为6种算法求解CBTSP实验。
表 2表示 GA、GAG与 HCGA求解大规模CBTSP问题的实验数据,表中n表示城市数量,m表示旅行者数目,最优解、最差解与平均解均为算法的求解质量,分别表示算法求解CBTSP运行10次的最优解、最差解和平均解,时间为运行 10次的平均求解时间。从表可以看出,HCGA和 GAG求解该问题的求解质量要好于GA。
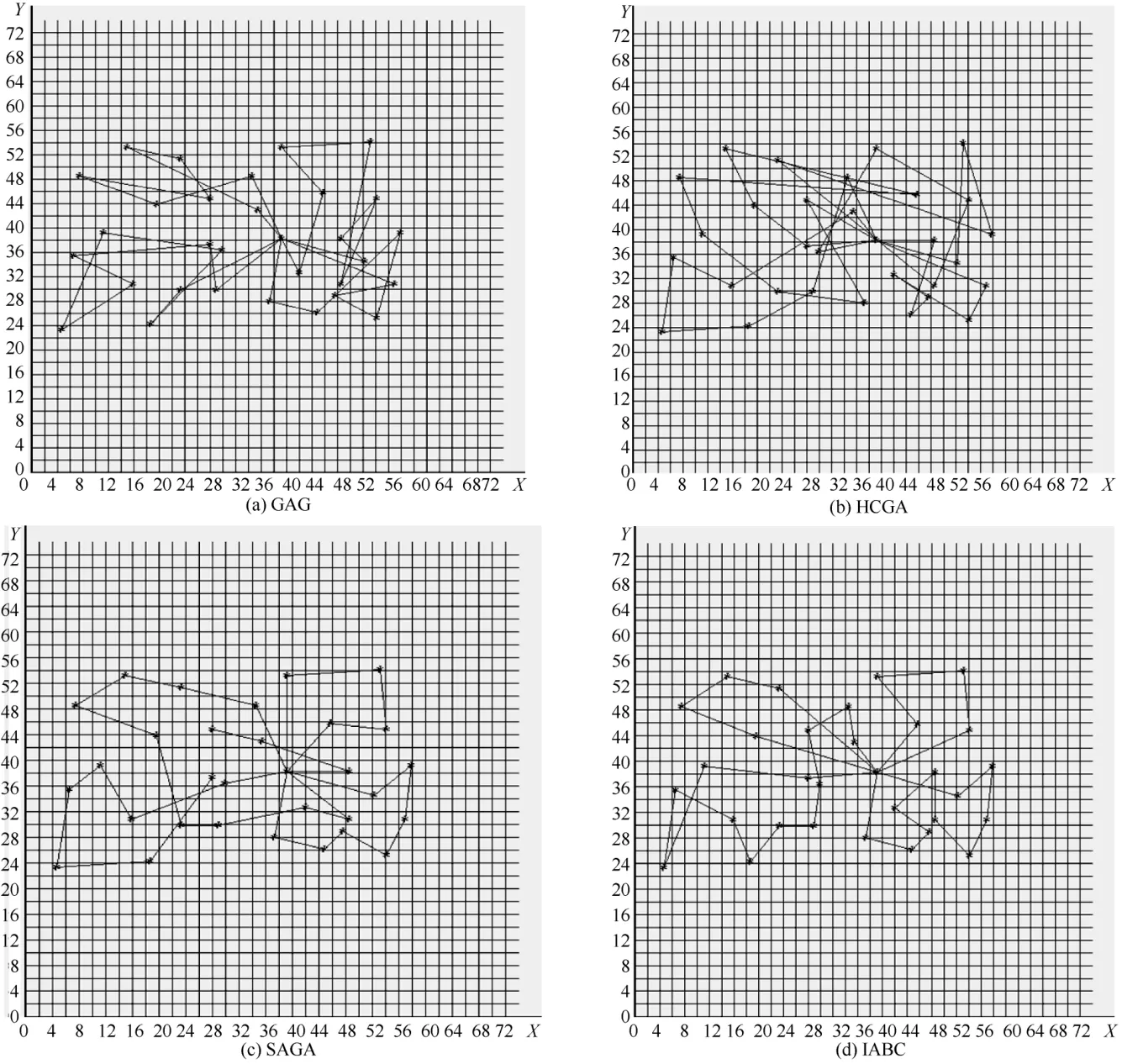
图2 当n = 31和m = 4时GAG、HCGA、SAGA与IABC求解CBTSP最优路线
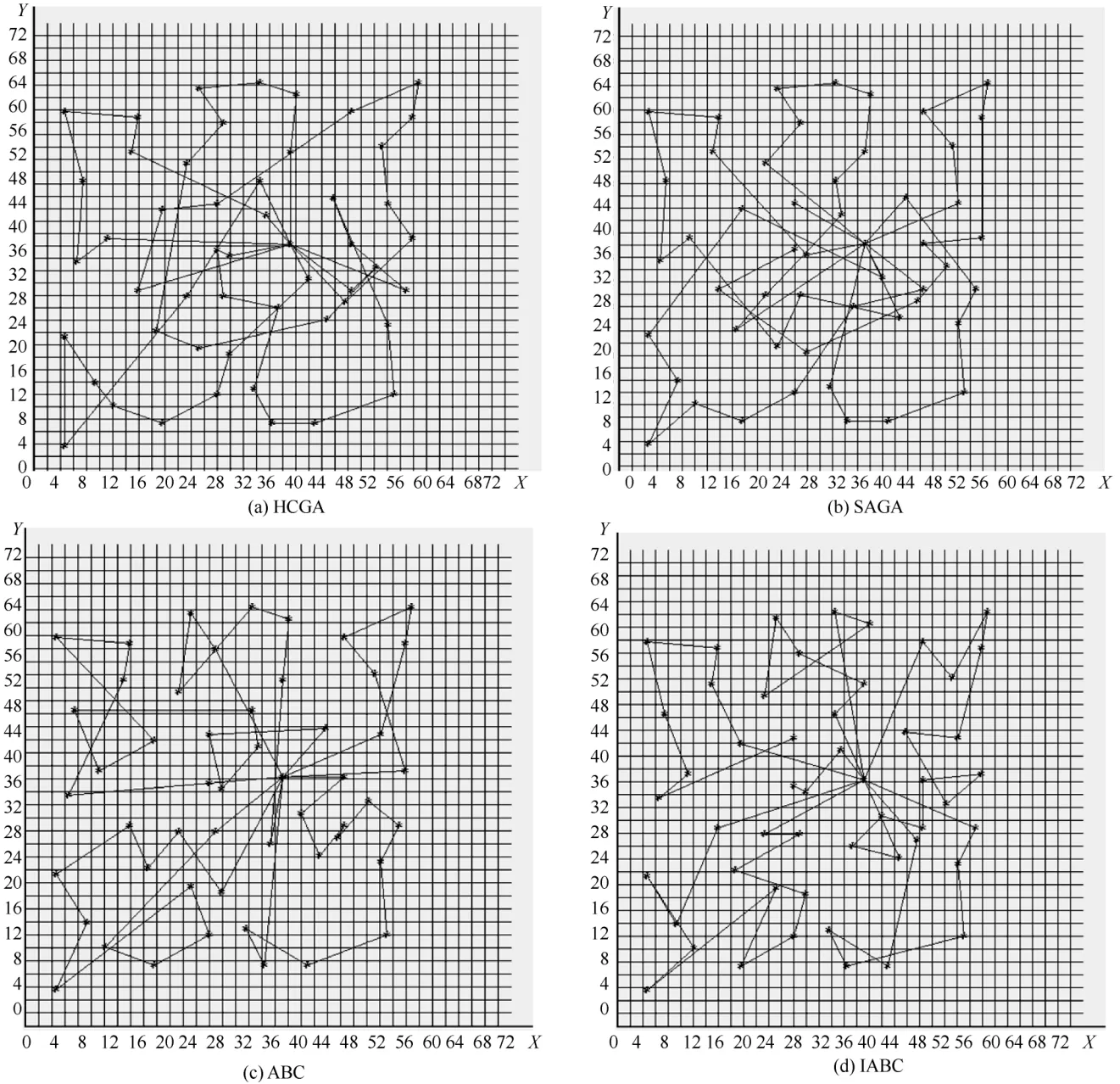
图3 当n = 51和 m = 5 时HCGA、SAGA、ABC与IABC求解CBTSP最优路线
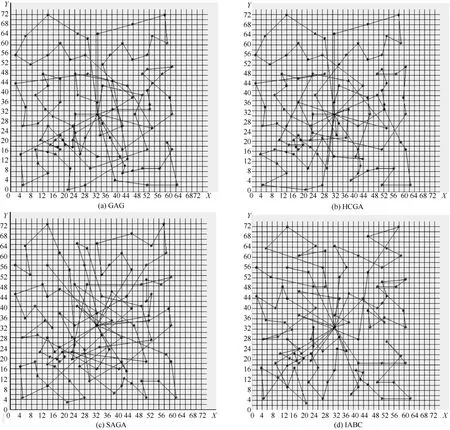
图4 当 n = 101与m = 7时 GAG、HCGA、SAGA与IABC求解CBTSP最优路线
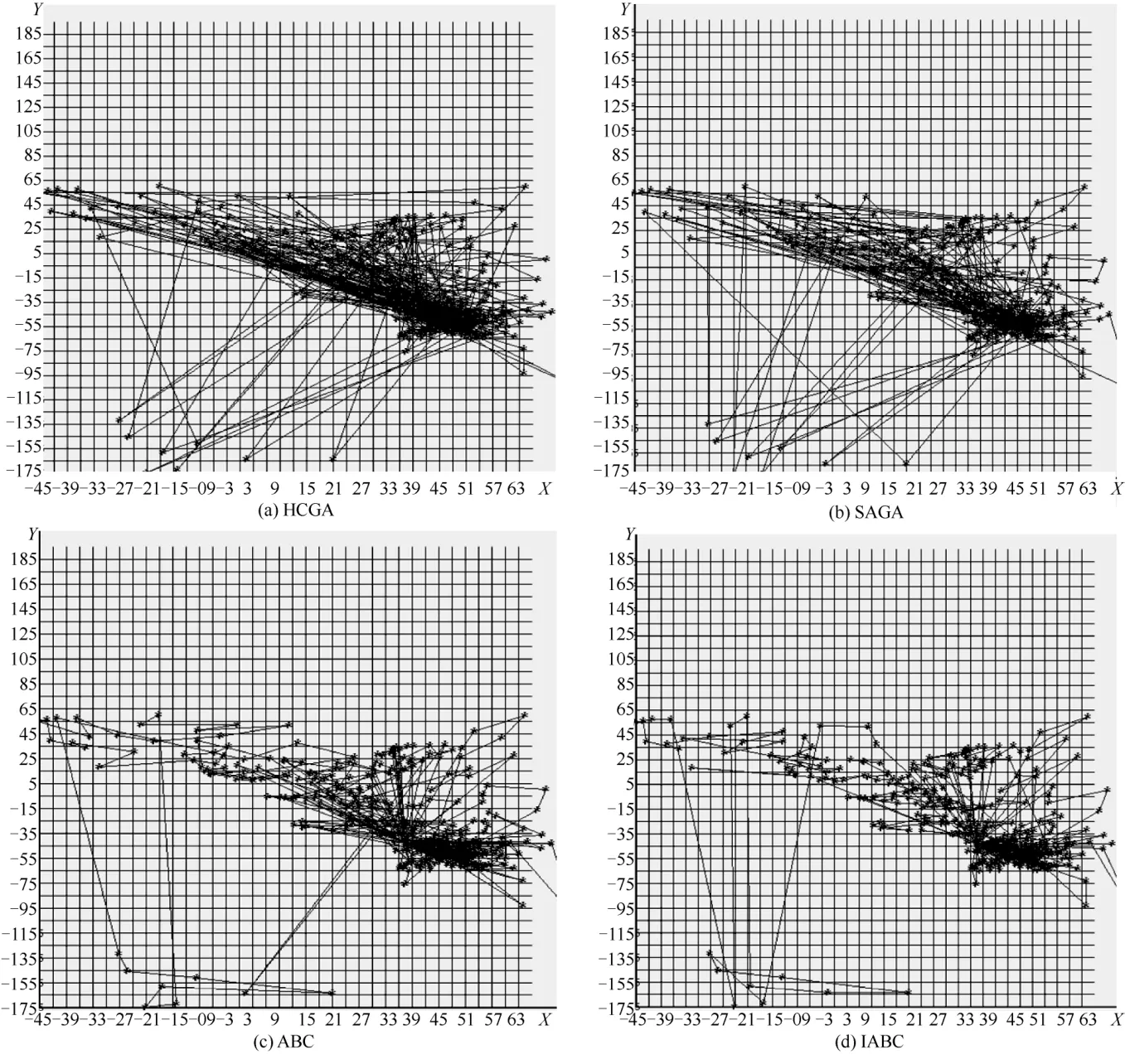
图5 当 n = 431与m = 40时HCGA、SAGA、ABC与IABC求解CBTSP最优路线
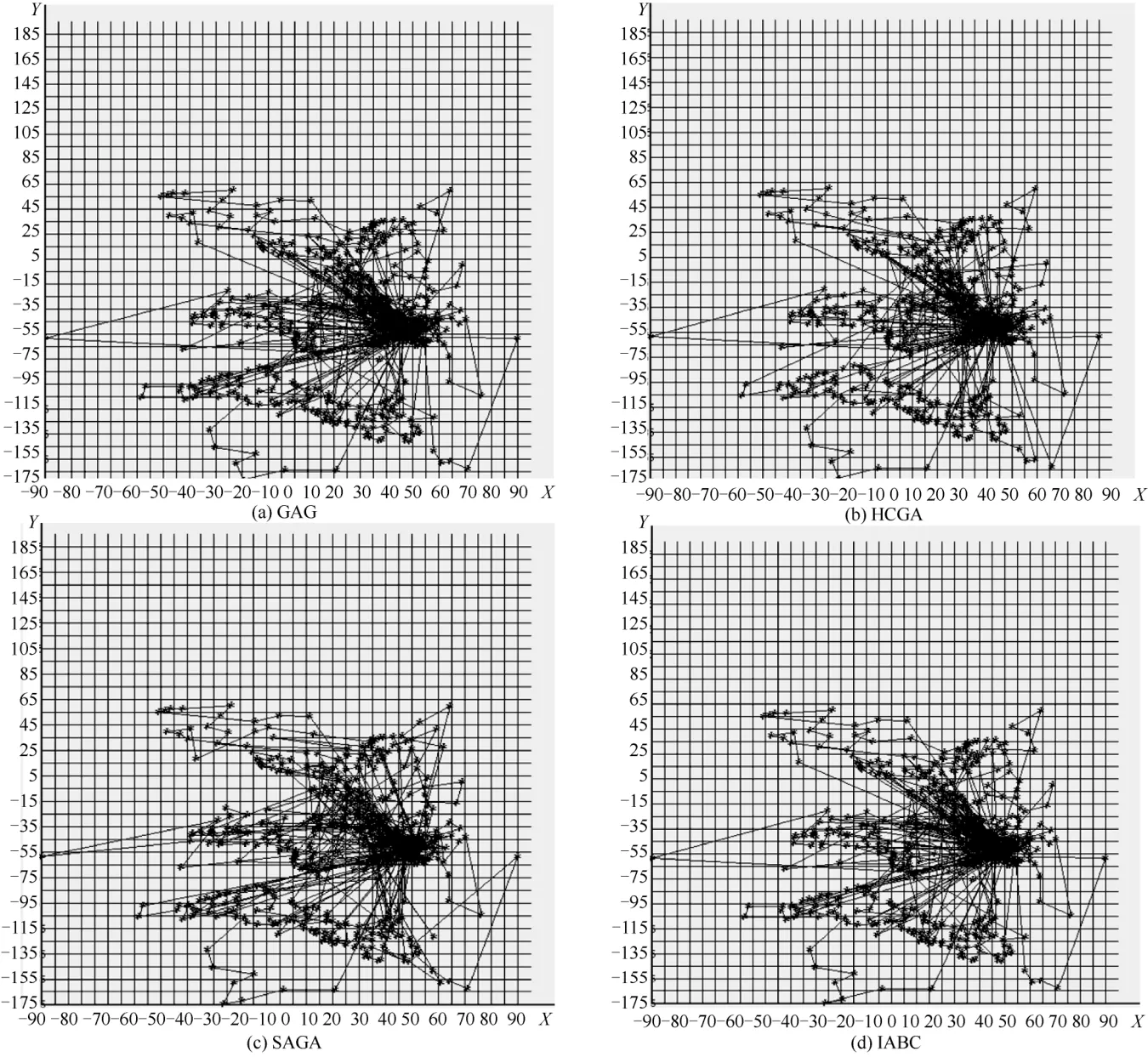
图6 当 n = 655与m = 33时 GAG、HCGA、SAGA与IABC求解CBTSP最优路线
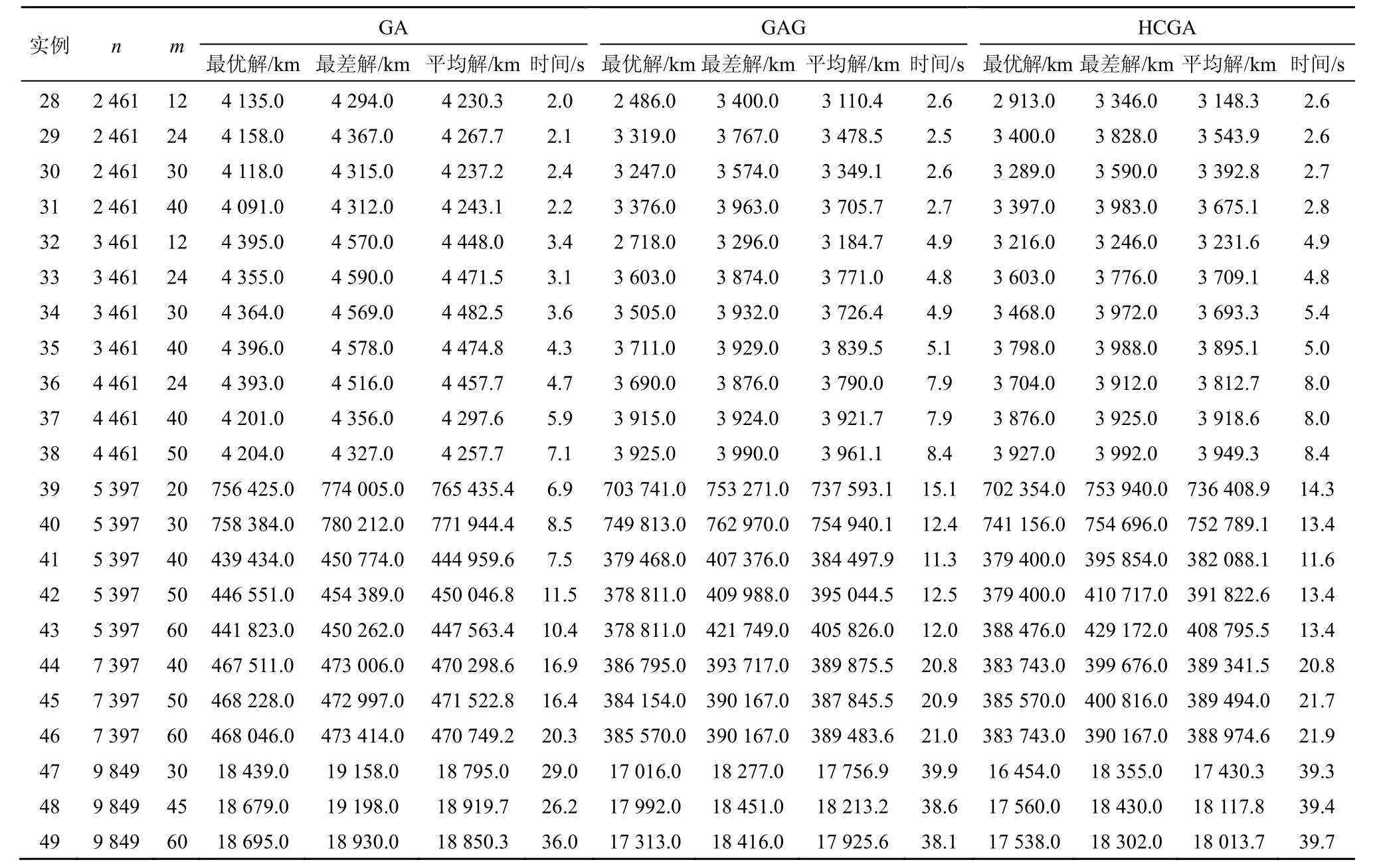
表2 GA、GAG与HCGA求解大规模CBTSP的实验数据
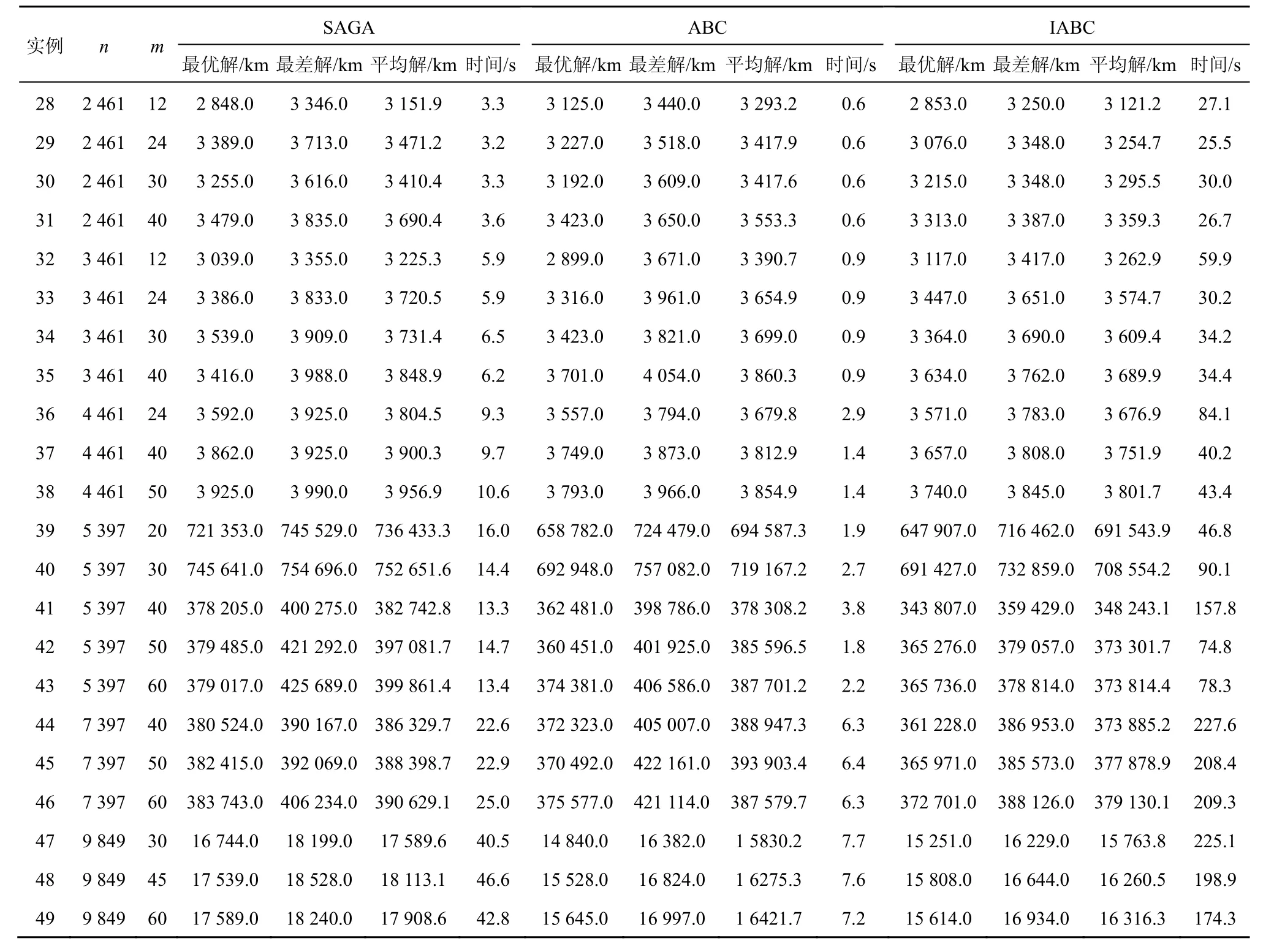
表3 SAGA、ABC与IABC求解大规模CBTSP的实验数据
表3的最优解、最差解与平均解均表示算法的求解质量,分别为算法求解CBTSP运行10次的最优解、最差解和平均解,时间为运行 10次的平均求解时间。从表3可以看出,IABC求解CBTSP问题的求解质量要好于SAGA和ABC。图7和图8分别为IABC与HCGA等6种不同算法在相同终止条件下,求解CBTSP的平均求解质量。
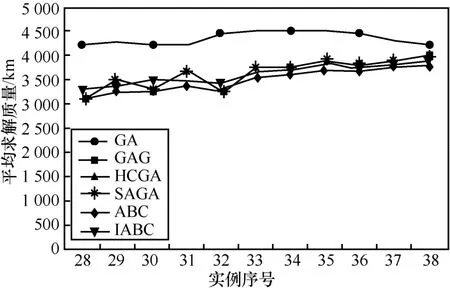
图7 算法求解CBTSP的平均求解质量对比
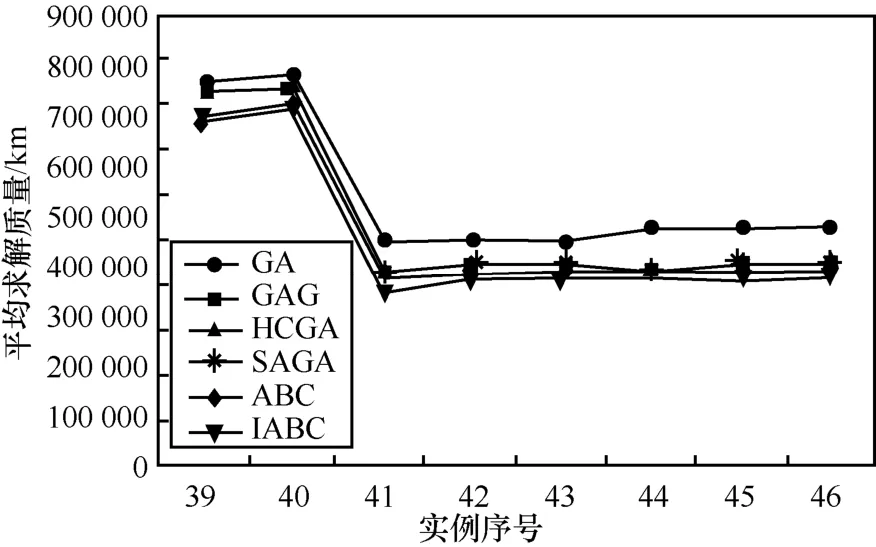
图8 算法求解CBTSP的平均求解质量对比
图7中,横轴表示实例的序号,每个序号对应着一个实例数据,纵轴表示算法的平均求解质量,单位为千米(km)。从图7可看出,IABC求解CBTSP的平均求解质量要好于 ABC、GA、GAG、HCGA和SAGA,表明改进蜂群算法求解该问题的有效性。IABC使用产生邻近解的方法来优化问题的解,求解该问题可产生更好的解,从图7可以看出,IABC的求解质量总体上要好于其他对比算法。
图8的横轴表示各个实例的序号,纵轴表示算法求解该问题的平均求解质量,单位为km。从图8可以看出,GA的求解质量最差,其他几种算法的平均求解质量相差不大,而且在使用不同的实例数据时每种算法的求解质量存在差异,在6种算法求解该问题中,IABC的平均求解质量表现较好。
表4和表5为相同的迭代时间为终止(停机)条件的5种算法求解大规模CBTSP问题的求解质量,从表4、表5的数据对比可看出,IABC的求解质量要好于GA、GAG、HCGA和SAGA。
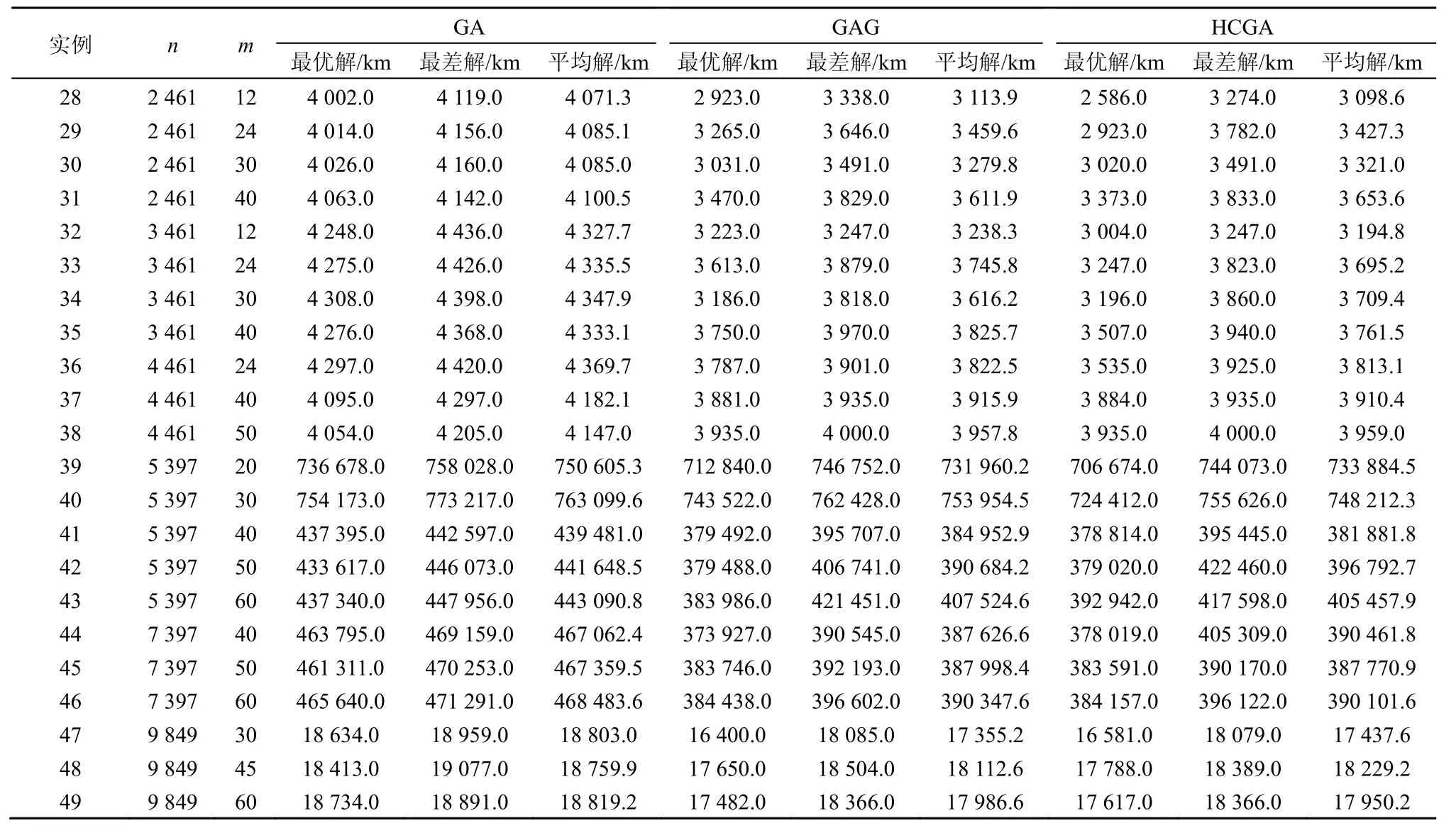
表4 GA、GAG与HCGA求解大规模CBTSP的求解质量
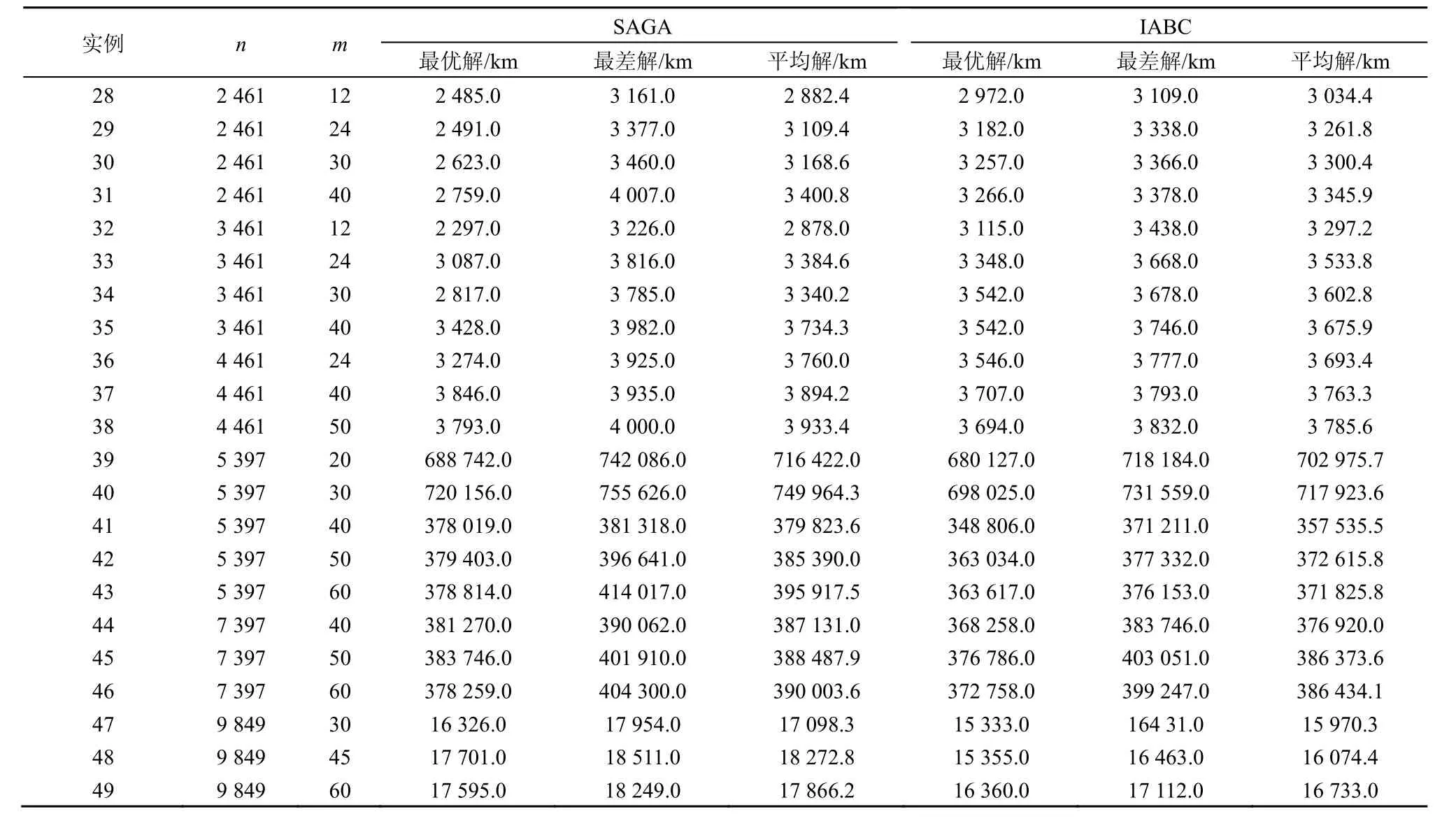
表5 SAGA与IABC求解大规模CBTSP的求解质量
为充分验证算法求解问题的有效性,用文献[21]实验的最优解的百分偏差PDbest和平均解的百分偏差PDav,对算法求解CBTSP问题进行显著性分析,结果如表6所示。
表6中PDbest计算方法为算法当前最优解减去已知最优解,然后除以已知最优解,再乘以 100;PDav计算方法是算法当前平均最优解减去已知平均最优解,然后除以已知平均最优解,再乘以100[21]。
表6为GA、GAG、HCGA、SAGA、ABC和IABC求解CBTSP的百分偏差数据,表中给出了最优解偏差PDbest和平均解偏差PDav,最后给出6种算法求解该问题的百分偏差数据的总均值。从该实验数据可看出,IABC的PDbest与PDav值在6种算法中最小,表示IABC求解质量在6种对比算法中最优。
IABC是先进的群体智能算法,在求解旅行商等组合优化问题可表现出较好的性能,从以上图表分析可看出,该算法求解大规模的CBTSP的求解质量要优于其他几个对比算法。IABC不仅使用ABC算法的优化机理,而且还运用产生邻近解的优化方法来进一步提升蜂群算法的求解质量,所以有更好的求解性能,因此求解大规模CBTSP问题的求解质量要好于ABC、GA、GAG、HCGA和SAGA算法。
5 结束语
针对现存实际问题,在CTSP与BTSP基础之上,本文探讨了一种 CBTSP路线规划分析模型,可以应用于含合作和独有任务并有部分重合工作区域的人员与车辆的路线优化问题,并将改进蜂群算法应用在求解 CBTSP之中。广泛的实验与分析表明,该算法对大规模 CBTSP问题的求解质量要优于相关的对比算法。
进一步的工作包括:1) 继续研究CBTSP问题及其相关的应用领域,使其在多任务协作、智能交通等领域有更加广泛的应用;2) 可以将本文的算法应用于求解其他大规模优化问题。
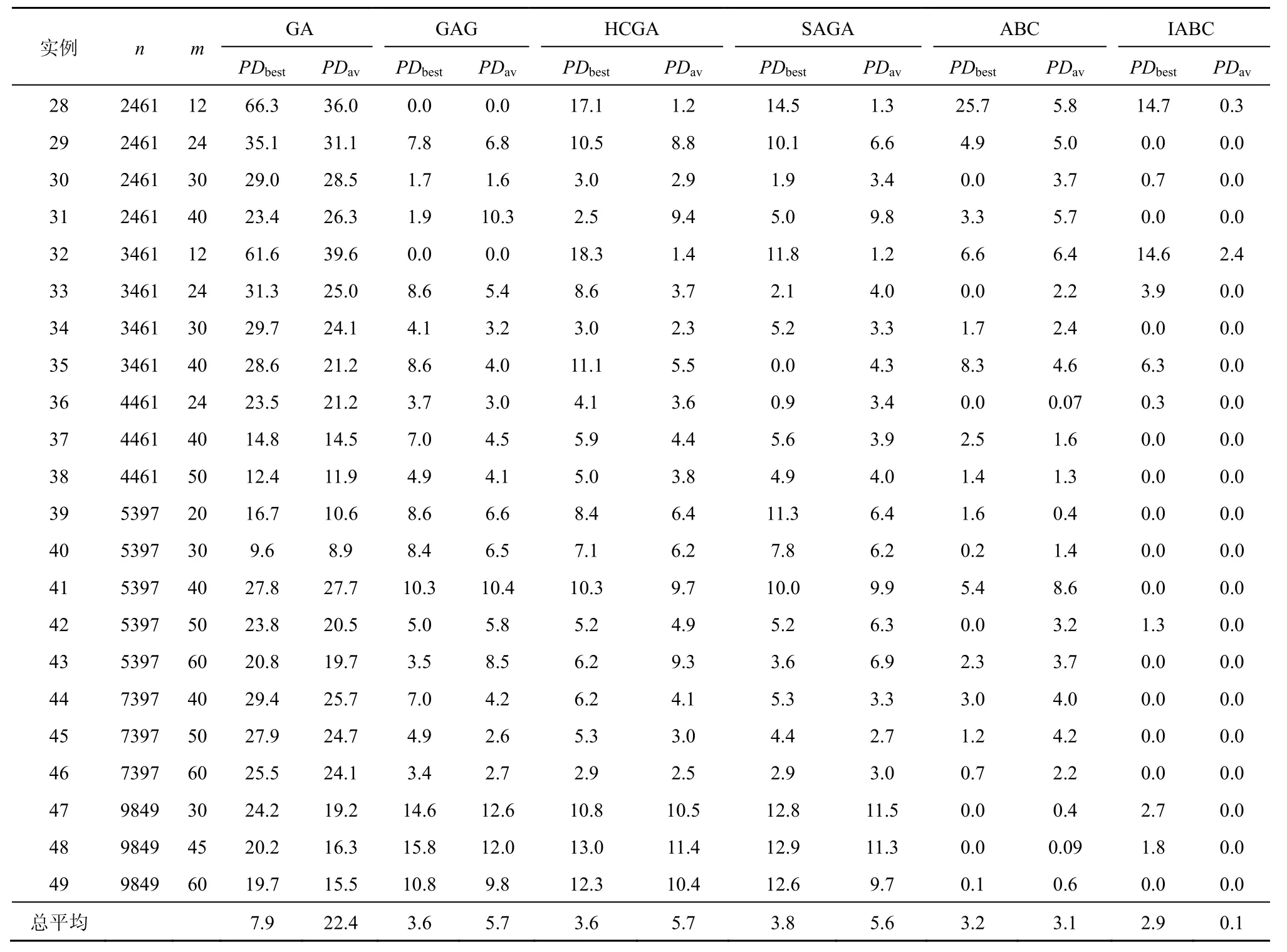
表6 算法求解大规模CBTSP问题的实验百分偏差数据

