信号特征谱表示与平稳随机信号谱分解统一的研究

王宏禹，邱天爽

（大连理工大学电子信息与电气工程学部，辽宁 大连 116024）

1 引言

信号展开主要有两大类，一类是傅氏级数展开，另一类是以正交的特殊函数为基的展开，通常特殊函数采用的是斯图谟—刘维尔（简称斯—刘）特征微分方程的特征函数Φ，与Φ相对应的特征值λ，称为微分方程的谱。为此，文献[1]推导出了斯—刘问题特征值的上界估计，文献[2]则进一步研究了特征值及特征函数的渐进估计，以及不连续斯—刘算子的自共轭性，但迄今尚未见到该特征谱表示的数学式。

特征方程可以用其方程算子来表示，有3种方程算子：1) 特征矩阵方程算子，以矩阵A表示；2) 特征微分方程算子，即斯—刘特征微分方程算子，以L表示；3) 与L相对应的积分方程算子，以K表示。这3种方程算子都是厄尔密特的，故对特征谱表示的研究，也就是对厄尔密特算子谱表示的研究。目前，只有对有限维条件下厄尔密特特征矩阵方程算子A的谱表示研究成果，该结果是由诺依曼提出的，并由其推广成为无穷维连续情况的谱表示，这种谱表示也称为诺依曼谱表示，解决了长期对原子谱数学理论问题的困扰。迄今为止，无穷维连续情况下微分算子L与积分算子K的谱表示是什么，L与K谱表示的关系又是什么，尚未见到文献介绍。为此，本文对这一问题进行了研究。

数学泛函分析具有高度统一性与广泛实用性，确定性信号与平稳随机信号的一些问题可以利用希尔伯特空间算子理论进行研究并统一起来。文献[3]对平稳随机信号谱分解采用希尔伯特空间酉算子法，给出其与信号特征谱表示在数学上的联系与统一，但存在一些数学物理意义不清楚的问题。为分析整个信号中对应每一频率的累积振幅(能量)分布情况，文献[4]采用希尔伯特边际谱来表征信号幅值随频率的变化。本文在此基础上对酉算子法进一步研究，结合信号特征谱得到更为清晰的数学解释，并给出利用与随机振幅简谐振动叠加法对比的研究方法。此外，给出了确定性信号与平稳随机信号两者的特征谱表示在数学上的联系与统一。信号特征谱表示是一个反映目标微动本质的较为稳定的特征，平稳随机信号谱分解是平稳随机信号时频分析的有力工具。这 2种谱表示式相似，在信号处理中可以互相借鉴。本文利用对平稳随机信号谱分解的随机振幅简谐振动叠加法及希尔伯特空间酉算子法进行研究，明确了信号特征谱表示与平稳随机信号谱分解的联系及数学上的统一，对于信号处理理论和应用中关于谱分析的研究具有指导意义。

2 厄尔密特算子与正交投影算子

为了研究方便起见，先扼要介绍数学文献上的厄尔密特算子与正交投影算子。

在n维线性空间Vn中，赋予2个n维矢量α与β的内积则称Vn是一个酉空间,也称为内积空间。在无穷维酉空间V中，若每个基本元素序列{fn(x) }均收敛于V中某一元素f(x)，即则称无穷维酉空间V是完备的，完备的无穷维酉空间称为希尔伯特空间(H空间)。在H空间中，矢量用函数表示，则矢量内积为

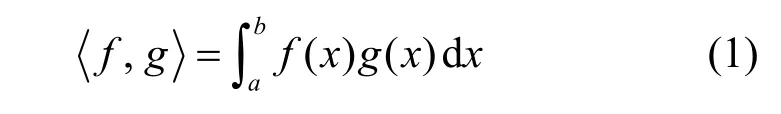
在这2种空间中，若线性算子L满足下列表示

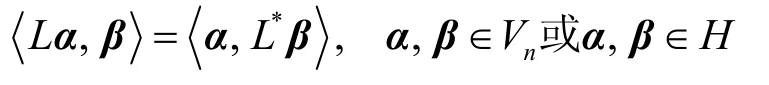
则L*称为L的共轭算子。当L=L*时，L称为自共轭算子或自伴随算子，也称为厄尔密特算子。厄尔密特算子L可以表示成一组正交投影算子Pi(i= 1 ,2,… ,∞)的线性组合，即

式(2)中 λi(i= 1 ,2,… ,∞)为L的不同特征值。正交投影算子Pi定义为：1) 幂等的，即PiPi=Pi；2) 正交的，即PiPj= 0 ,i≠j；3) 归一化的，即(对于酉空间)，

3 厄尔密特矩阵算子的特征分解与谱表示

N×N阶厄尔密特矩阵算子A的特征方程为

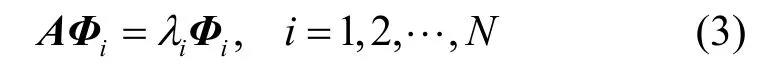
其中，列矢量Φi(i= 1,2,… ,N)称为特征解(假定特征解为正交归一化)，相应的实数 λi(i= 1,2,… ,N)为特征值。将式(3)写为矩阵形式，有

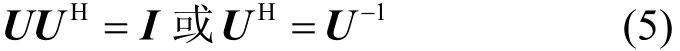
即U是酉矩阵，由式(4)与式(5)，得

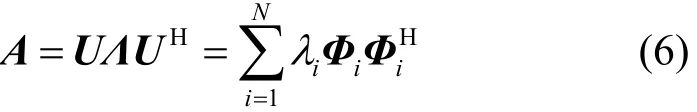
1) 当式(6)中特征值λi按降序顺序排列时，即λ1≥ λ2≥ … ≥ λN，式(6)的表示称为厄尔密特矩阵算子A的特征分解。对长方形矩阵，需用奇异值分解处理。因这两者在信号处理中均有重要应用，并为众所熟知，本文不对其详细论述。

2) 当式(6)中特征值λi按递增顺序排列时，即λ1≤ λ2≤ … ≤ λN时，式(6)的表示称为厄尔密特矩阵算子A的谱表示，现详细介绍如下。

若对角矩阵Λ主对角线上按λi大小按递增顺序处理，则Λ是唯一确定的，可唯一地表示为如式(7)所示的分解式。

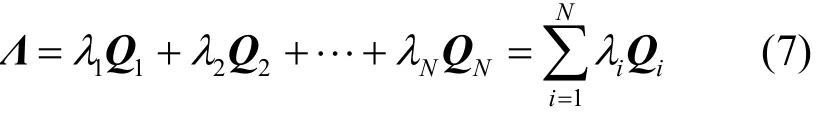
其中，Qi(i= 1,2,… ,N)为对角阵。Qi(i= 1,2,…,N)的和为单位矩阵，即

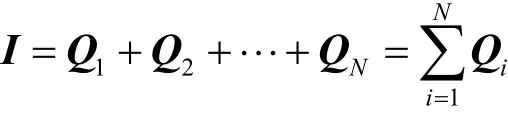
此外，Qi为厄尔密特幂等矩阵，因QiQi=Qi，且Qi是正交的，即QiQj= 0，故Qi是正交投影矩阵。

现定义矩阵Pi为

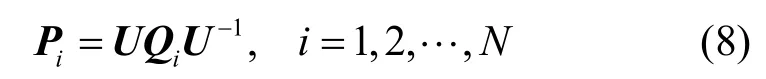
将式(7)和式(8)代入式(6)，可得式(9)。

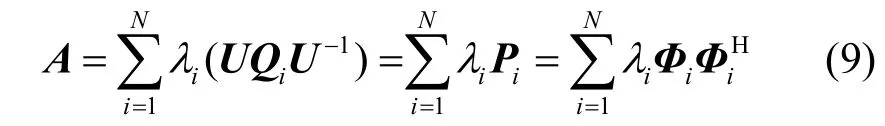
4 厄尔密特微分算子与积分算子的谱表示

4.1 特征微分方程及其谱表示

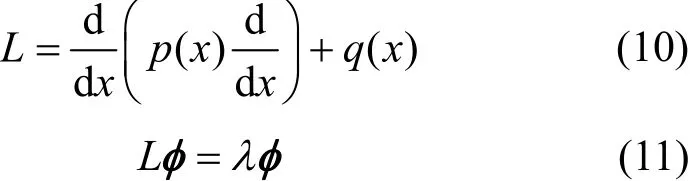
在信号处理中，信号展开基函数所用的正交特殊函数，均可用如式(10)所示形式微分算子L的特征微分方程(斯—刘微分方程)[5]得到，如式(11)所示。其中，p(x)、q(x)在所论区间都是连续的，且p(x) ＞ 0；λ称为特征值，由无穷个λi组成，它们都是实数；与λi对应的φi称为特征函数，它们是正交的，即

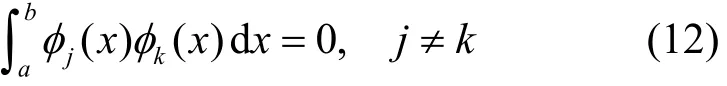
将特征值按增序排列，可得到一个无限序列λ1, λ2,… ,λi,…这个序列称为特征微分方程的谱。

在满足适当边界条件下，对 2个函数f(x)与g(x)，式(10)所示的微分算子L满足如式(13)所示的内积关系。

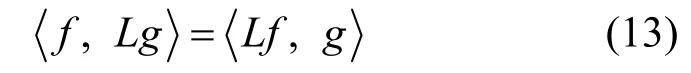
因此，式(10)所示的微分算子L是厄尔密特的。

4.2 厄尔密特微分算子及其特征微分方程格林函数的关系

任意函数f(x)可表示为正交的归一化特征函数 φk(x)的无限展开式，如式(14)所示。

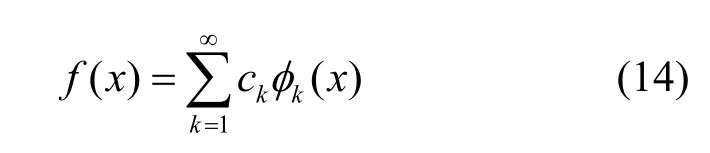
若 φk(x)是正交归一化的，即

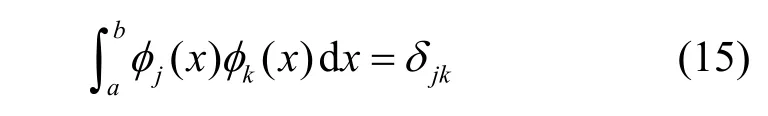
利用式(15)可得展开系数ck为

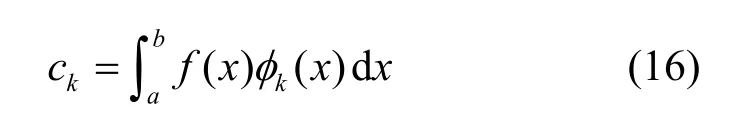
式(14)所示的f(x)可以表示为以式(10)所示的微分算子L的非齐次微分方程，如式(17)所示

的解。根据线性系统的理论，u(x)为系统的输入，f(x) 为输出。根据式(11)、式(13)和式(17)，将g=φk代入式(13)中，得

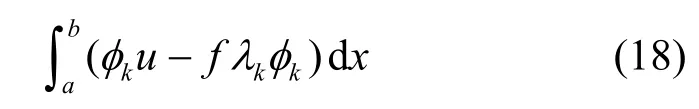
利用式(9)可得系数ck的表示式，为

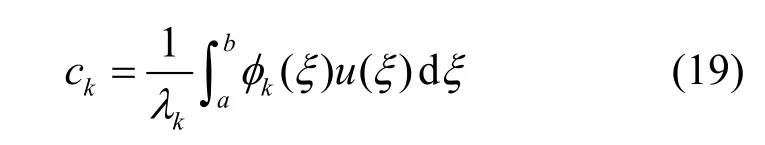
将式(19)所示的ck代入式(14)，可得

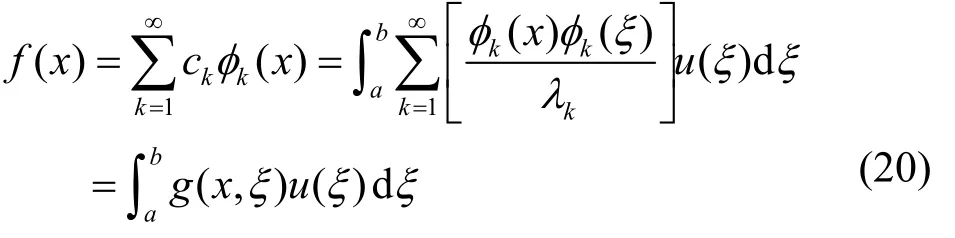
其中，g(x,)ξ为

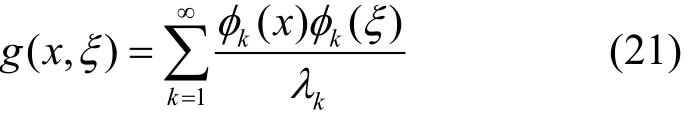
因式(20)为输入u(ξ)与输出f(x)的积分形式，故g(x,ξ)是与时变系数微分算子L对应的线性时变系统的格林函数[6]。当输入u(x) = δ ( ξ -x0)时，由式(20)得到输出，如式(22)所示。

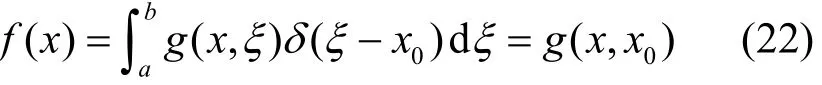
即对线性时变系统，格林函数g(x,x0)为于x0处施加单位脉冲而在x处所得的输出f(x)。由式(17)和式(22)可得

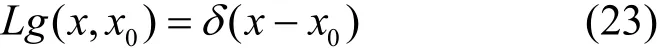
式(23)表明，厄尔密特微分算子L是其特征微分方程格林函数g(x,x0)的逆算子[7]。

4.3 积分算子方程与特征积分方程

在数学中，积分算子K方程定义为

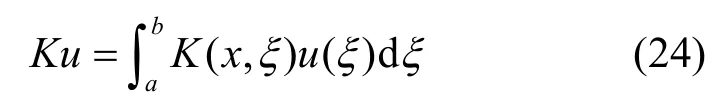
其中，K(x,ξ)称为核函数。根据线性系统的理论，若u(x)为输入，f(x)为输出，其输入与输出关系的积分表示式应该为

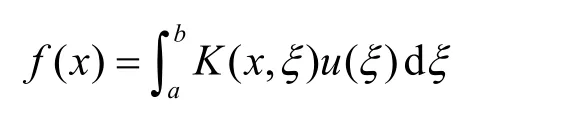
若K(x,ξ)选择为如式(21)所示的特征微分方程的格林函数g(x,ξ)，则积分算子K的输入与输出关系方程为

而微分算子L输入与输出关系的方程如式(22)所示，将式(25)代入式(22)，可得LK=1，故当K(x, ξ ) =g(x, ξ)时，微分算子L与其相对应的厄尔密特积分算子K是互逆的，即，由此可得对应的特征积分方程表示为

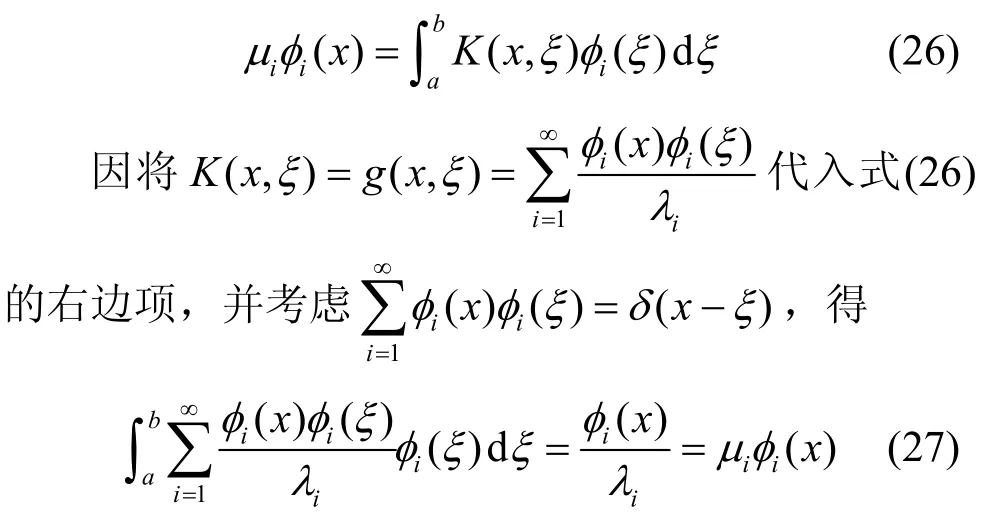
其中，μi为特征积分方程的特征值，与对应的特征微分方程特征值λi是互逆的，即

长期以来，人们对于如式(11)特征微分方程是否存在与其对应的特征积分方程认识不够清晰。由于式(11)是线性时变系数微分方程，对其采用通常积分方法，除调和微分方程外，难以得到与其对应的特征积分方程表示式。本文通过采用特征微分方程格林函数g(x,ξ)和特征积分方程核函数K(x,ξ)的关系，则可以解决这个认识不清的问题[8]。另外，目前对特征积分方程的深入研究，只限于其核函数K(x,ξ)是可分离的或退化的，即K(x,ξ)=这种形式，也需要得到进一步的研究解决。

4.4 厄尔密特微分算子与积分算子的谱表示之间的统一关系

根据4.2节的研究，厄尔密特微分算子L与其格林函数g(x,ξ)的关系为Lg(x, ξ )= δ (x- ξ )，当ξ=x时，可得

而厄尔密特微分算子L与其对应的厄尔密特积分算子K的关系为

由式(28)与式(29)，得K的表示式为

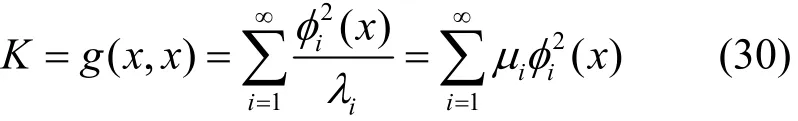
即式(30)就是厄尔密特积分算子K的谱表示式，其数学物理意义如下。

1) 当积分算子K方程的核函数K(x,ξ)=g(x,ξ)与输入u= δ (x- ξ )时，由式(24)与式(25)得

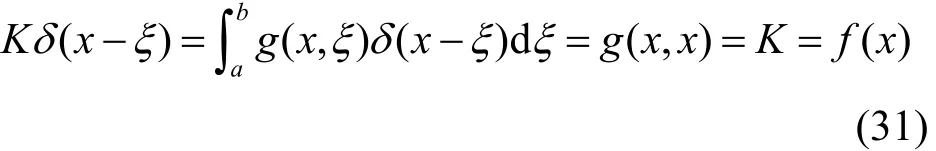
其中，f(x)为输出。

2) 根据格林函数定义，线性时变系统的格林函数g(x,ξ)为ξ时刻输入δ( ξ)于时刻x的输出，线性时不变系统的格林函数g(x,ξ)与时刻ξ无关，仅与x-ξ有关，即g(x, ξ ) =g(x- ξ )。现g(x,x)应该定义为线性时变系统于x-ξ时刻输入单位脉冲δ(x-ξ)在x时刻的输出。

这样，如式(30)所示的厄尔密特积分算子K的谱表示可以认为是格林函数g(x,x)与g(x,x)对应的输出信号f(x)的谱表示式。

将式(15)归一化特征函数 φi(x) (i= 1 ,2,…)的形式表示成离散和形式，得

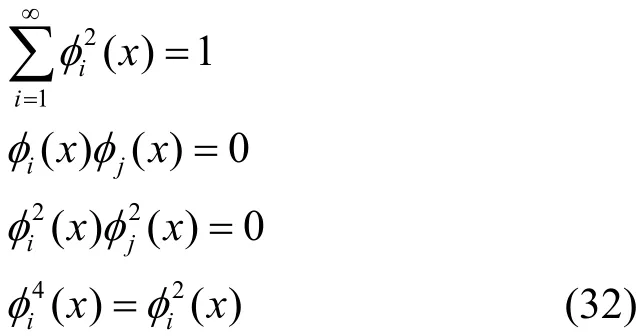
这种以投影算子Pi(i= 1 ,2,…) 表示不仅具有一般化意义，并且谱是按一定顺序排列的意义也更加清晰。

由式(29)、式(32)和式(33)可得厄尔密特微分算子L的谱表示式，如式(34)所示。

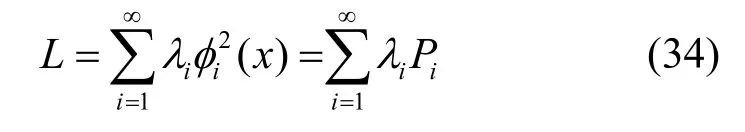
由式(33)与式(34)可见L与K谱表示式在数学上的表示是相同的，因此，为了研究方便，下文对它们统一表示为，但应明确λi为L或K何者的特征值。

式(33)与式(34)是离散和或无限级数表示式，若它们平均收敛成为一函数，可表示成为积分式。为此，先介绍一取值为正交投影算子Pi的函数E(λ)，其定义如式(35)所示。

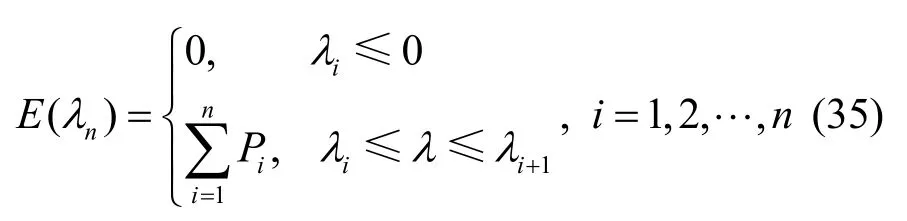
由此可得

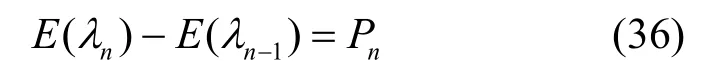
当 λi(i= 1 ,2,…) 无限接近时，可利用勒贝格积分，即

其中，lim表示趋向非常小的划分区间[i+1,i],i= 1 ,2,…。由式(35)和式(36)可得

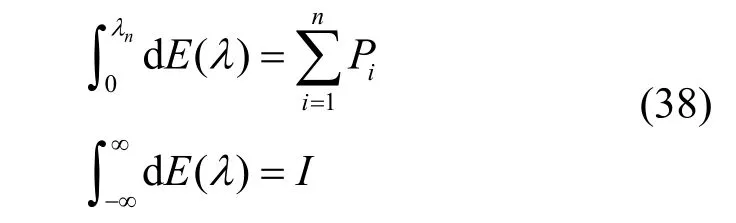
其中，I为恒等算子。这样，式(33)与式(34)可分别表示为

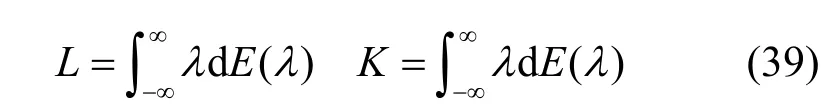
由式(31)可知，对厄尔密特积分算子K，K=f(x)，因此，式(39)中K还可表示为输出信号f(x)的特征谱表示式，即

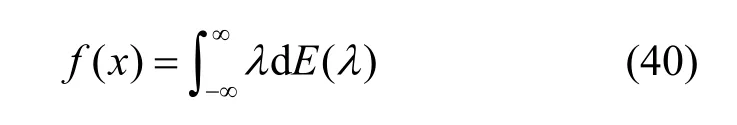
5 2种不同谱理论在数学上的联系与统一

谱理论分为正弦谱理论与特征谱理论（即厄尔密特算子谱理论），前者是平稳随机信号谱理论，也称为维纳谱理论，后者是原子谱理论，也称为诺依曼谱理论。这2种谱表示式相似，可在数学上统一起来。下面依据对平稳随机信号谱分解理论研究方法，对其进行讨论。

5.1 随机振幅简谐振动叠加法

对平稳随机信号x(t)，若其自相关函数rxx(τ)是周期性的，可以通过傅里叶级数展开，得到x(t)的谱分解式，如式(41)所示。

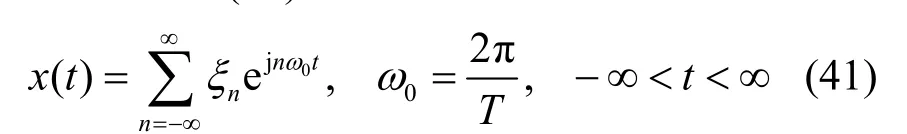
其中，T为周期；展开系数ξn是正交(不相关)的随机变量，可由式(42)确定。

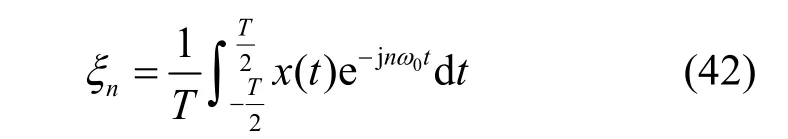
当rxx(τ)是非周期的，式(41)中ξn不再正交，且该式不再对每一个t都成立。因此，这种情况的平稳随机信号x(t)一般是不能用傅里叶级数展开得到其谱分解的。已有证明，若ω0足够小，可找到一个级数xˆ(t)，如式(43)所示。

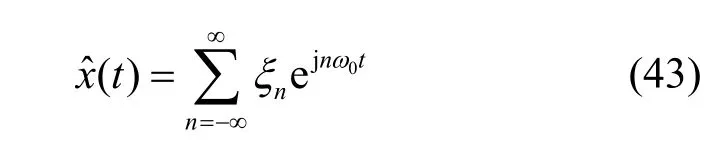
给出x(t)一个比较精确的均方逼近，有

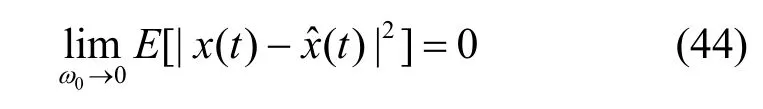
即当ω0→0时，x(t)仍可用傅里叶级数展开。若令

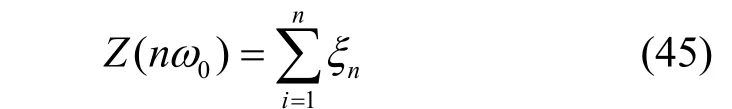
则有

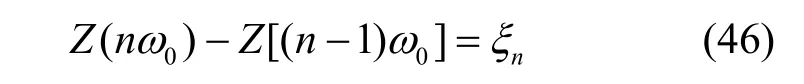
将式(45)代入式(46)中，得

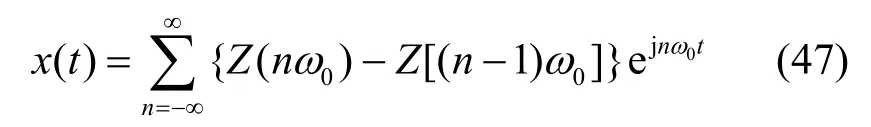
上式ω0→0的极限形式，即各相邻谱线间距非常小时，可由勒贝格积分得到随机积分，如式(48)所示。

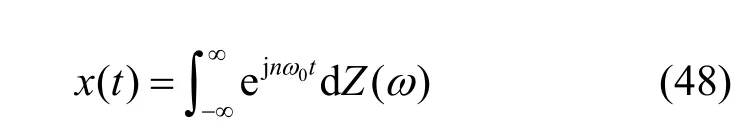
即为平稳随机信号x(t)的谱分解。该式表明x(t)是由无限个频率由小到大连续变化的随机幅度简谐振动叠加而成。

由式(40)与式(48)，信号f(x)特征谱表示与平稳随机信号x(t)的谱分解相对应的关系如表 1所示。

由表1可见，信号f(x)特征谱表示与平稳随机信号x(t)谱分解在数学表示上相同，因此，可将它们统一起来。

5.2 酉算子法

为了更清楚地了解平稳随机信号谱分解的酉算子法，先介绍研究它的广义调和分析法。

5.2.1 广义调和分析法

平稳随机信号是功率型信号，是不存在傅里叶变换的，需要用广义变换进行调和分析研究。平稳随机信号x(t)的广义变换定义为

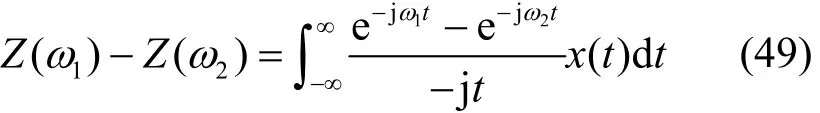
设 ω1= ω + ε ,ω2= ω - ε ，由式(49)可得

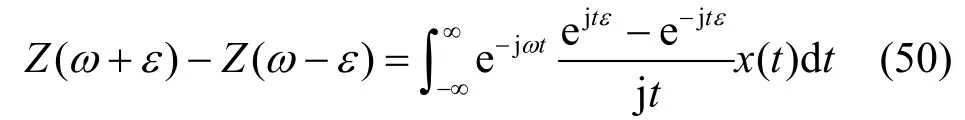
这样，Z( ω + ε ) -Z(ω - ε )是过程的傅里叶变换，即

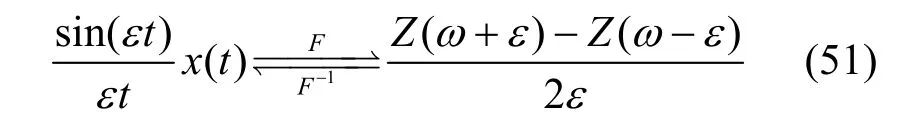
由式(51)可得

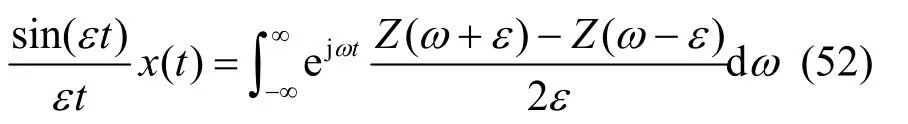
令ε→0，式(52)的左侧项趋于x(t)，右侧项虽然Z(ω)不可微，但可写为斯蒂尔吉斯(J. J. Stieltjes)积分，即对x(t)的谱分解式，如式(53)所示。

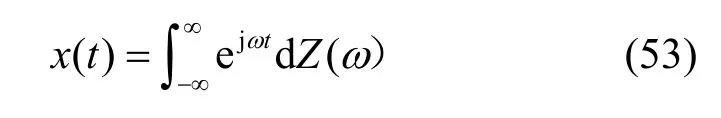
下面，从线性时不变系统的输入输出关系对广义变换进行研究。理想带通线性系统如图1所示，系统函数如式(54)所示。

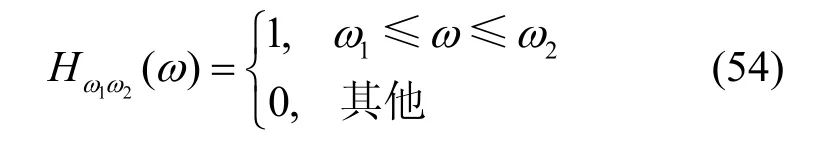
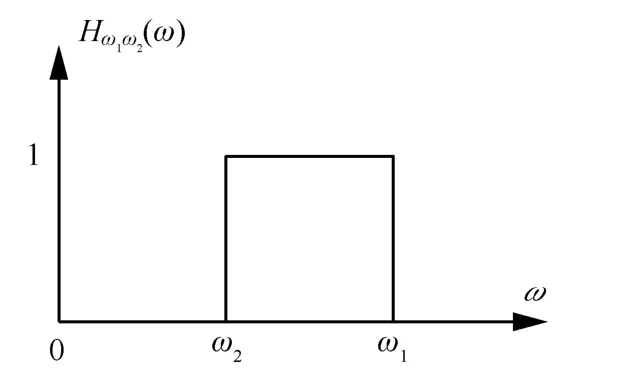
图1 理想带通线性系统

它的脉冲函数hω1ω2(t)为

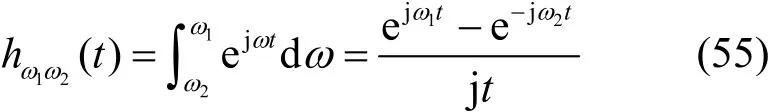
表1 f(x)特征谱表示与x(t)谱分解式相对应的关系

当x(t)输入此线性系统时，其输出yω1ω2(t)为

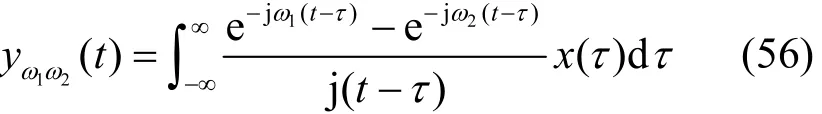
当t=0时，有

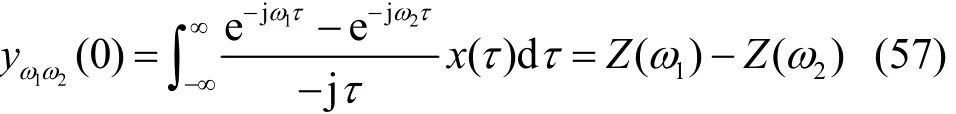
即x(t)的广义变换相当x(t)输入理想带通线性时不变系统式(54)的输出于零时刻的结果，由于x(t)输入的是理想带通线性系统，可无失真地得到x(t)的输出，因此

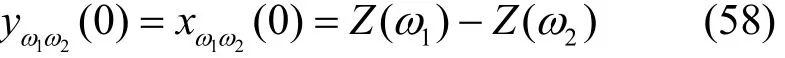
对于理想全通线性系统，可视为由图2所示的系列理想带通线性系统所组成，如式(59)所示。

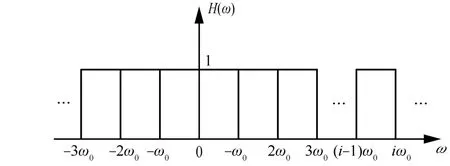
图2 理想全通线性系统组成

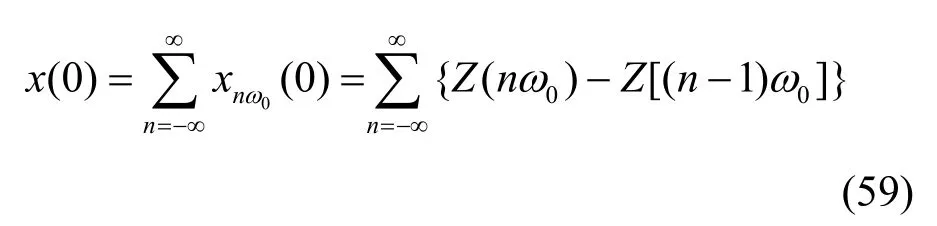
当ω0→0时，式(59)可表示为

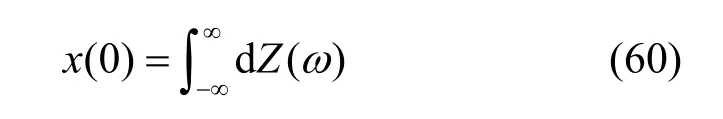
由式(46)与式(48)得

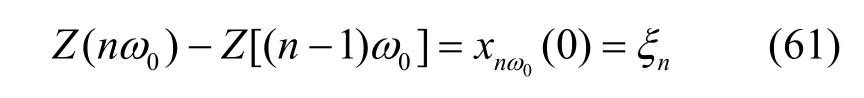
应注意，为了表示方便起见，将x(n-1)ω0,nω0(0)简写为xnω0( 0)，而当ω0→0时，xnω0( 0)由式(61)容易得出如式(62)所示的正交关系。

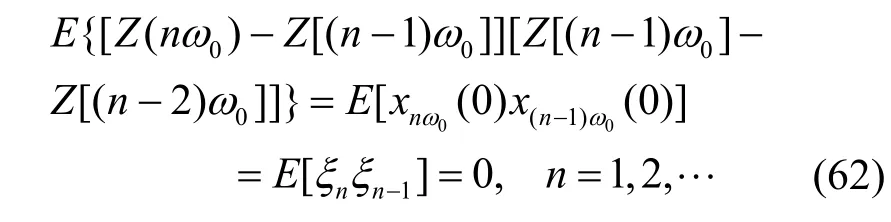
根据上述研究，可对平稳随机连续信号x(t)的谱分解式(48)的物理意义做进一步说明为，x(t)是由无限个不同频率(即连续变化频率)互相正交随机幅度的复正弦波叠加而成，各不同频率复正弦波的随机幅度

5.2.2 酉算子法

现有文献对平稳随机过程的希尔伯特空间的介绍，仅限于由具有二阶矩随机变量x与y的内积定义的，即

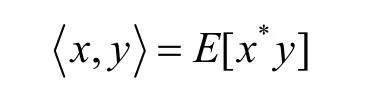
因此，本文改由为离散时间平稳随机信号x(k)谱分解的研究。若x(k)是零均值的，其自相关函数rxx(m)为

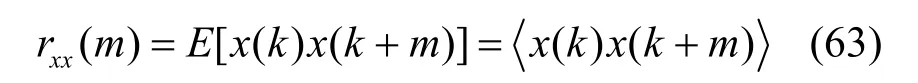
即rxx(m)只依赖时移m，而与时间k无关。

目前在数学文献中，只见到对酉空间Vn中酉算子L的介绍，其定义为

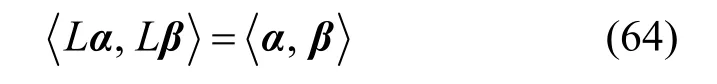
其中，α、β为Vn空间中任意2个矢量。对平稳随机过程的希尔伯特空间，尚未见到其酉算子U的明确介绍，本文套用式(64)定义来研究。由式(63)可知rxx(m)与时间k无关，只依赖时移m，因此，平稳随机过程元素x(k)可以认为由时移算子U递推产生的，即

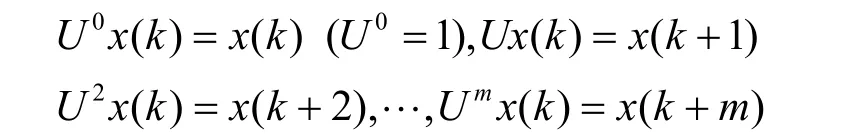
rxx(m)可表示为

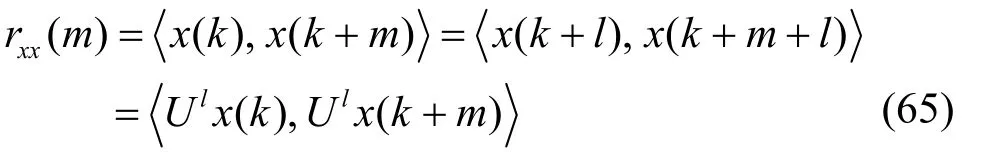
因此，时移算子U满足式(65)定义，是酉算子。此外，由于rxx(m)是偶函数，即

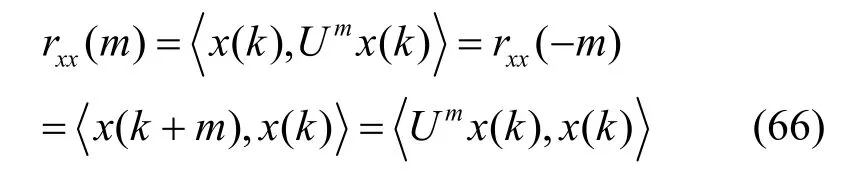
U算子还符合厄尔密特算子定义的要求，可将其表示为如式(67)所示的酉算子谱表示式。

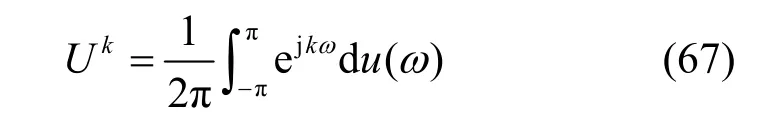
当k=0时，U0=1，表明U0是恒等算子，于是可得

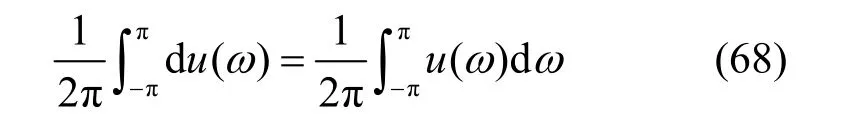
式(68)表明u(ω)是理想全通线性系统或理想全通滤波器，可将其视为由一系列理想带通滤波器所组成，如图2所示。在酉算子谱表示中，理想带通滤波器unω0(ω)(为u(n-1)ω0,nω0(ω )的简写，n=1,2,…)系列就是正交投影算子Pn=unω0(ω),n= 1 ,2,… 系列，因为它们满足正交投影算子的要求，即PnPn-i=0,

对离散平稳随机信号x(k)，可用时移算子U递推来研究，即x(k) =Uk x( 0)，而用U算子谱表示来研究，可得出x(k)的谱表示式，下面就来推导。

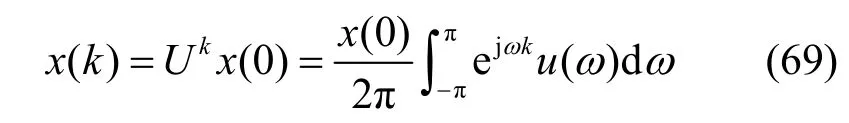
为了解清楚起见，将上式写成离散和形式

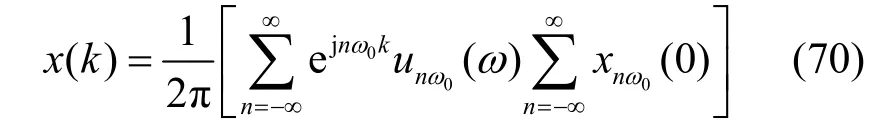
因unω0(ω )是理想带通滤波器，只能将同一频段的xnω0( 0)无失真地输出，于是，由式(70)得

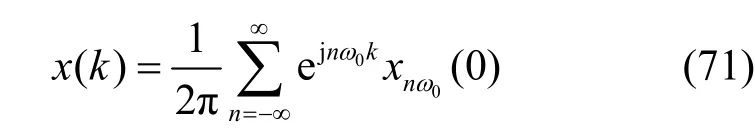
利用式(59)并将其写成连续形式，得x(k)的谱分解式，如式(72)所示。

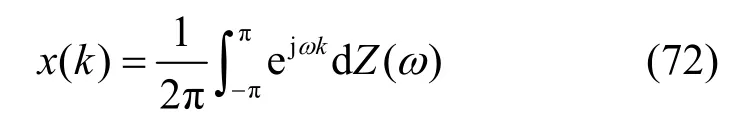
另外，将式(60)代入式(69)，也可得出式(72)为

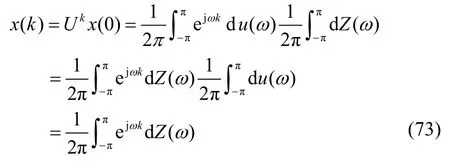
由上述研究，在离散平稳随机信号x(k)的自相关函数研究中，引入时移算子U，该算子成为随机变量希尔伯特空间的酉算子。这个酉算子的谱表示与函数希尔伯特空间微分算子L与积分算子K的谱表示相似，其中U与L或K对应， ejω与λ对应，通过这种联系，可将信号特征谱表示与平稳随机信号谱分解在数学上统一起来。

6 2种信号特征谱表示的联系与统一

确定性信号f(x)与平稳随机信号x(t)均有其各自的信号特征展开与特征谱表示，因此存在全似在数学上是否有联系及统一的问题。平稳随机信号的特征展开与特征谱表示已有研究，即为人们所熟知的卡—洛展开[9-10]，直接给出平稳随机信号与确定性信号特征展开及特征谱表示的关系，如表2所示。

由表2可见，确定性信号f(x)与平稳随机信号x(t)的特征展开与特征谱表示在数学上表示相同，它们可统一起来。

7 结束语

特征微分方程的格林函数g(x,ξ)在信号特征展开与特征谱表示研究中具有重要的意义与作用，解决了正交多项式的斯—刘微分方程没有与其对应的特征积分方程的问题。本文的g(x,x)，其意义为线性时变系统于x-ξ时刻输入单位脉冲而在x时刻所得的输出。

特征微分算子L与g(x,x)的关系为Lg(x,x)=1，即L为g(x,x)的逆算子。当特征积分算子方程的核函数时，特征积分算子K与特征微分算子L的关系为LK=1，即L与K是互逆关系。

特征微分算子L与特征积分算子K均是厄尔密特的，厄尔密特算子L与K的谱表示可统一为离散和形式和连续函数形式，即L或K=

表2 2种信号特征展开与特征谱表示的关系

对平稳随机信号x(t)的谱分解利用与随机振幅简谐振动叠加法的对比及对文献[3]提出的酉算子法做进一步研究，得出与信号特征谱表示相同的数学表示式，从而可将两者统一起来。

由此可见，确定性信号与平稳随机信号两者的特征谱表示明显地存在数学上的统一关系，这对于深化对信号谱分析本质的理解有重要意义。