辐射状均压槽气浮支承静态性能仿真研究
于普良,李 双,胡江山,郭永兴,丁 喆,刘怀广
(1.武汉科技大学冶金装备及控制教育部重点实验室,湖北 武汉 430081;2.武汉科技大学机械传动与制造工程湖北省重点实验室,湖北 武汉 430081)
0 引言
气浮支承作为高端制造业中的核心支承技术,长期以来被世界各国列为产品研发和技术应用的重点[1-4]。表面节流技术是提高静压气体轴承静态性能的重要技术手段之一[5-9]。表面均压槽结构产生的节流效应会改变气膜内压强分布,从而提高气浮支承的承载力和刚度[10-15]。诸多学者在关于均压腔、环形槽和T型槽等表面结构对气浮支承的静态性能影响方面取得了不少成果[16-22]。目前,关于辐射状均压槽气浮支承结构的研究鲜有报道。
为此,设计了一种辐射状均压槽气浮支承结构。其周向和径向截面分别呈三角形和扇形。建立了辐射状均压槽的气浮支承有限元模型,研究辐射状均压槽对气浮支承静态性能的影响。研究表明,辐射状均压槽可以显著提高气浮支承的静态性能。
1 辐射状均压槽气浮支承CFD模型
1.1 辐射状均压槽气浮支承结构
气浮支承结构如图1所示。

图1 气浮支承结构图
辐射状均压槽气浮支承呈圆形,采用小孔节流、均压腔节流和均压槽节流三种节流方式。小孔出口处的均压腔呈圆形,辐射状均压槽的周向截面和径向截面分别为三角形和扇形。高压气体Ps通过节流孔后,以均压腔为中心沿径向向四周扩散,最终排到大气环境,外部大气压力为P0。气浮支承半径为Rf=50 mm,节流孔高度为Ho=0.3 mm,节流孔直径为Do=0.2 mm,均压腔直径为Dc=3 mm,均压腔深度为Hc=0.1 mm,气膜厚度为Hf,均压槽角度为θg=2°、4°、6°、8°、10°,辐射状均压槽直径为Rg=5 mm、15 mm、25 mm、35 mm、45 mm,均压槽数目为Ng=2、4、8、16、32,均压槽深度为Hg=0.02 mm、0.04 mm、0.06 mm、0.08 mm、0.10 mm。
为了提高计算效率,选取四分之一流体计算域,计算域划分为四个区域:节流口、均压腔、均压槽和气膜。气体流场计算域如图2所示。

图2 气体流场计算域示意图
为了精确地分析三维CFD流体模型,选择标准k-ε湍流模型和可压缩性气体模式;动量和能量等均选择二阶迎风型隐——显差分格式;进出口湍流密度设置为7%;流孔进气口设置为恒定压力进口Ps;节流孔出气口设置为大气压力P0;左右剖面设置为对称边界条件。进口设置为压力进口压力边界条件;出口设置为压力出口边界条件;其余均为无滑移无传热固体壁面。
1.2 气体润滑控制方程
气体静压润滑雷诺方程的一般表达式[21]为:
(1)
式中:p为气膜压力;h为气膜厚度;u1为气浮支承上表面的运动速度;u2为气浮支承下表面的运动速度;μ为气体动力黏度。
在稳态的情况下,气体从气浮支承进口的边界流入气膜,然后从出口的边界排出,其流入质量与流出质量应相等[22],则:
(2)
式中:μ为气体质量流量;dμ为其微元流量;入口边界条件gi(x,y)=0,(i=1,2,3,…,m);出口边界条件φj(x,y)=0。
气浮支承承载力为:
(3)
气浮支承刚度为:
(4)
1.3 辐射状均压槽气浮支承CFD模型
为了提高网格质量和计算精度,采用六面体结构网格划分。气膜厚度方向设置为10层以上网格,节流孔入口区域和过渡区处均采用网格加密处理,网格总数目大于200万。气浮支承CFD模型如图3所示。

图3 气浮支承CFD模型
气体遵循理想气体定律,其密度随状态方程的改变而改变,温度为25 ℃。空气黏度设置为1.79×10-5kg/(m·s);分子质量设置为29.00×10-3kg/mol;比热容设置为1.01×103J/(kg·K);热导率设置为2.42×10-2W/(m·K)。
2 仿真结果及分析
无均压槽气浮支承(Ho=0.3 mm,Hf=10 μm,Dc=0 mm,Rg=0 mm,Do=0.2 mm,θg=0°,Ng=0,Hg=0 mm,Hc=0 mm,Ps=0.5 MPa),辐射状均压槽气浮支承(Ho=0.3 mm,Hf=10 μm,Dc=3 mm,Rg=35 mm,Do=0.2 mm,θg=6°,Ng=4,Hg=0.10 mm,Hc=0.1 mm,Ps=0.5 MPa)的压力分布云图如图4所示。由图4可以清晰看出,辐射状均压槽气浮支承的压力分布优于无均压槽气浮支承,辐射状均压槽气浮支承可以提高气浮支承的承载力。

图4 压力分布云图
2.1 均压槽深度影响规律
气浮支承的其他参数设置为恒定值 (Hf=10 μm,Rg=35 mm,θg=6°,Ng=4,Hc=0.1 mm,Ps=0.5 MPa),辐射状均压槽深度与气膜厚度对气浮支承的承载力、质量流量和刚度变化曲线如图5所示。
由图5(a)可见,承载力随着气膜厚度的增加逐渐降低,当气膜厚度一定时,承载力随着均压槽深度的增加而增大。由图5(b)可见,气体质量流量随着气膜厚度的增加逐渐增加,当气膜厚度一定时,气体质量流量随着均压槽深度的增加而增加。由图5(c)可见,均压槽深度对气浮支承刚度的峰值影响不显著,但是影响刚度峰值所在的气膜厚度,均压槽深度越深其刚度峰值所在的气膜厚度越大。因此,气浮支承均压槽深度影响承载力、气体质量流量和刚度。

图5 不同均压槽深度的承载力、质量流量和刚度变化曲线
2.2 均压槽半径影响规律
当气浮支承的其他参数为恒定值时(Hf=10 μm,θg=6°,Ng=4,Hg=0.10 mm,Ps=0.5 MPa),辐射状均压槽半径与气膜厚度对气浮支承的承载力、气体质量流量和变化曲线影响如图6所示。由图6(a)可见,承载力随着气膜厚度的增加逐渐降低,当气膜厚度Hf<7 μm且厚度一定时,承载力随着均压槽半径的增加而增加,变化幅度较大;当气膜厚度Hf>7 μm且厚度一定时,承载力随着均压槽半径的增加先增加后减小。由图6(b)可见,气体质量流量随着气膜厚度增加逐渐增大,当气膜厚度一定时,气体质量流量随着均压槽半径的增加而增加。由图6(c)可见,均压槽半径影响刚度峰值及其刚度峰值所在的气膜厚度,气浮支承刚度的峰值随着均压槽半径增加而增加,气浮支承刚度峰值所在的气膜厚度随着均压槽半径的增加而降低。因此,适当增加气浮支承均压槽的半径可以增大承载力和刚度,但是要以牺牲一定的气体质量流量为代价。
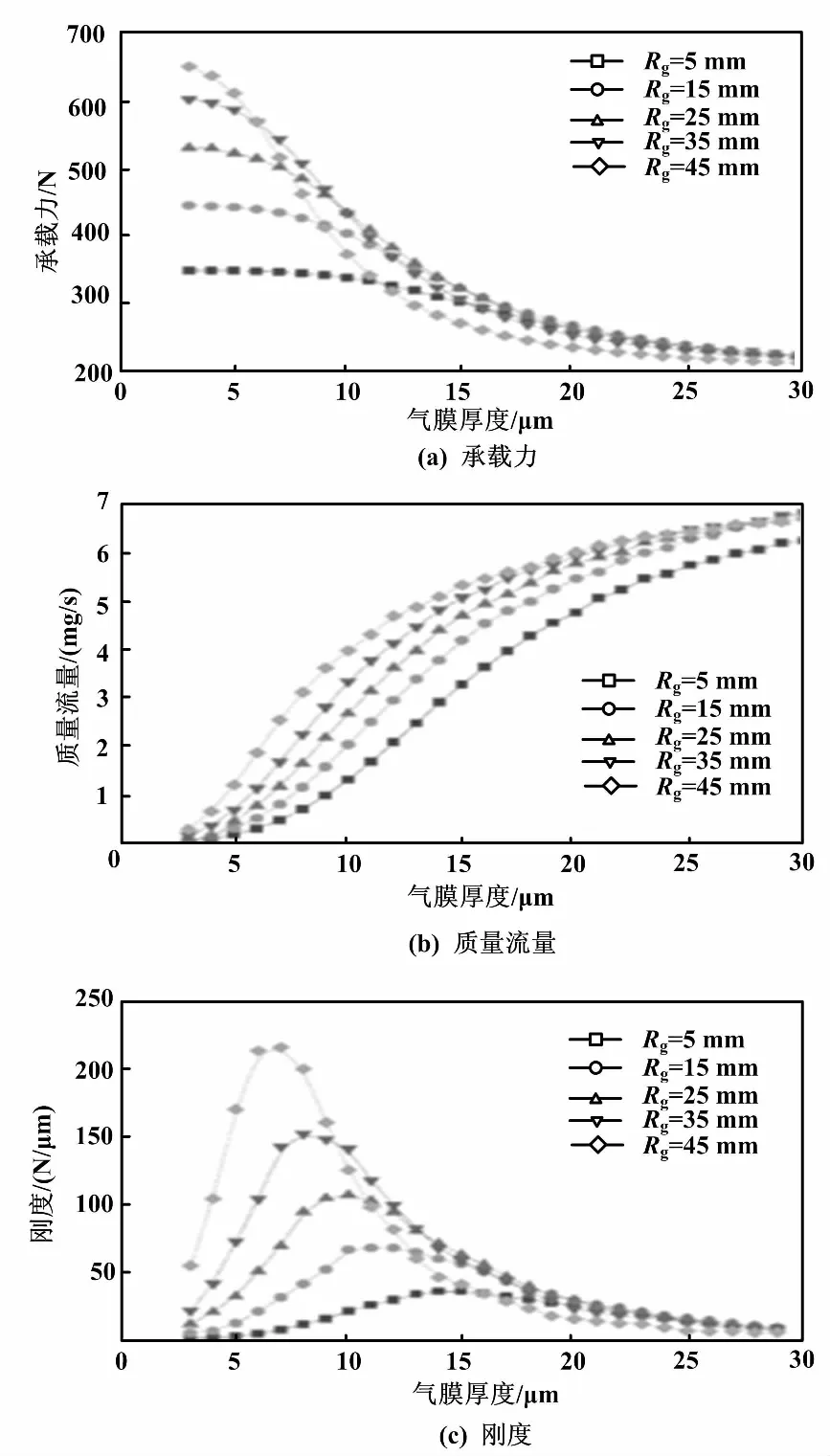
图6 不同均压槽半径的承载力、质量流量和刚度变化曲线
2.3 均压槽数目影响规律
当气浮支承的其他参数为恒定值时(Hf=10 μm,Rg=35 mm,θg=6°,Hg=0.10 mm,Ps=0.5 MPa),辐射状均压槽数目与气膜厚度对气浮支承的承载力、刚度和质量流量变化曲线如图7所示。由图7(a)可见,承载力随着气膜厚度的增加逐渐降低,当气膜厚度一定时,承载力随着均压槽数目的增加而增加。由图7(b)可见,气体质量流量随着气膜厚度的增加逐渐增加,当气膜厚度一定时,气体质量流量随着均压槽数目的增加而增加。由图7(c)可见,均压槽数目影响气浮支承刚度峰值显著,对其刚度峰值所在的气膜厚度影响不大,气浮支承刚度的峰值随着均压槽数目的增加而增加。因此,增加气浮支承均压槽数目可以增大承载力和刚度,但是要以牺牲一定的气体质量流量为代价。

图7 不同均压槽数目的承载力、质量流量和刚度变化曲线
2.4 均压槽角度影响规律
当气浮支承的其他参数为恒定值时(Hf=10 μm,Rg=35 mm,θg=6°,Hg=0.10 mm,Ps=0.5 MPa),辐射状均压槽角度与气膜厚度对气浮支承的承载力、气体质量流量和刚度变化曲线如图8所示。由图8(a)可见,承载力随着气膜厚度的增加逐渐降低,当气膜厚度一定时,承载力随着均压槽角度的增加而增加,变化幅度并不大。由图8(b)可见,气体质量流量随着气膜厚度增加逐渐增加,当气膜厚度一定时,气体质量流量随着均压槽角度的增加而增加。由图8(c)可见,均压槽角度对气浮支承刚度峰值及其气膜厚度有一定的影响,气浮支承的刚度峰值随着均压槽角度的增加而增加,气浮支承刚度峰值所在的气膜厚度随着均压槽角度的增加而增加。因此,气浮支承均压槽的角度影响气浮支承承载力、气体质量流量和刚度。

图8 不同均压槽角度的承载力、质量流量和刚度变化曲线
2.5 供气压力影响规律
当气浮支承的其他参数为恒定值时(Hf=10 μm,Rg=35 mm,θg=6°,Ng=4,Hg=0.10 mm),辐射状均压槽供气压力与气膜厚度对气浮支承的承载力、刚度和质量流量的影响如图9所示。
由图9(a)可见,承载力随着气膜厚度的增加逐渐降低。当气膜厚度一定时,承载力随着供气压力的增加而增加,变化幅度较大。
由图9(b)可见。气体质量流量随着供气压力的增加逐渐增加,当气膜厚度一定时,气体质量流量随着供气压力的增加而增加。
由图9(c)可见,气浮支承供气压力对气浮支承刚度影响显著,对其刚度峰值所在的气膜厚度影响不大。气浮支承的刚度的峰值随着供气压力的增加而显著增加。
因此,增加气浮支承供气压力可以增大承载力和刚度,但是要耗费较大的气体质量流量。

图9 不同供气压力承载力、质量流量和刚度变化曲线
3 结束语
分析了不同供气压力情况下,辐射状均压槽气浮支承的均压槽结构参数对气浮支承的静态性能的影响。研究结果表明:均压槽可以显著提高气浮支承的承载力、刚度,但会以牺牲一定的气体质量流量为代价;其承载力和刚度峰值随均压槽深度、数目、角度和供气压力的增加而增加,供气压力和均压槽数目对承载力和刚度的影响尤为显著;在一定范围内,气浮支承承载力和刚度峰值随均压槽半径的增加而增加,且影响气浮支承刚度峰值所在的气膜厚度。

