二维编织C/SiC复合材料板疲劳损伤分析

陈天雄， 张铮， 王奇志， 林彗星

(北京航空航天大学 航空科学与工程学院, 北京 100083)

近年来，C/SiC陶瓷基复合材料逐渐发展，越来越多地被应用于航天器、运载火箭等高速飞行器中[1-2]。C/SiC陶瓷基复合材料使用碳纤维作为增韧补强材料，克服了其陶瓷基体脆性大的缺点，拥有较高的强度和硬度、良好的抗高温氧化和抗腐蚀特性，耐热冲击性高，因此主要作为耐烧蚀和耐高温结构材料[3]，应用前景广阔。国外从20世纪末开始便对陶瓷基复合材料开展了大量实验与理论研究[4-7]，而国内的相关研究开展稍晚，主要为不同应力比以及高温、水氧等各种环境下的疲劳试验研究[8-10]，但相关理论研究较少，工程适用性不高。

本文基于损伤力学理论，提出了2种形式的损伤演化方程，考虑了应力和损伤的耦合作用，结合商用有限元软件对该材料的板模型进行了损伤模拟和定性分析，方法适用性良好，对工程设计及疲劳寿命预估具有理论指导意义。

1 损伤演化方程

材料内部所存在的微小缺陷，例如微裂纹、错位、空洞等，导致材料宏观力学性能的劣化，称之为损伤。损伤力学诞生至今，已得到了长足发展，张行等[11-12]将损伤力学应用于金属构件的疲劳寿命预估分析，形成了比较完备的疲劳损伤力学理论体系。宏观力学损伤研究的基本思路是：定义一个与损伤程度相关的不可逆的连续场变量，即损伤场[13]，通过力学方法构建含损伤的材料本构关系，建立相应的损伤演化方程，并使用材料标准试样疲劳试验得到的疲劳寿命(S-N)曲线拟合得到相应参数，进而计算材料损伤及预估结构疲劳寿命。

损伤度通常用材料弹性模量的折减程度表示：

(1)

式中：D为材料的损伤度；E和ED分别为材料在损伤发生之前和之后的弹性模量。

对于各向同性材料，一般根据等温过程下的热力学原理，定义损伤驱动力Y为应变能密度W对损伤度偏导的负值，将受脉动循环载荷材料的损伤演化方程[14]写为

(2)

式中：N为加载周次；Ymax为脉动载荷下最大应力所对应的最大损伤驱动力；a、m和n为材料损伤参量，可根据材料的疲劳寿命曲线拟合得到。

若定义等效应力σe为

(3)

式中:σx、σy、σz、τyz、τzx、τxy分别为x、y、z方向的正应力和切应力;μ为材料泊松比。则损伤驱动力Y可进一步表示为

(4)

由于复合材料内部结构拥有纤维、基体、界面等不同结构组分，其损伤形式与普通金属材料不同。复合材料结构常见的损伤形式有基体开裂、基体纤维界面脱胶、纤维断裂和层间分层等[15]。这些损伤的萌生和演化对材料宏观力学性能和使用寿命起着决定性的作用，同时，由于复合材料本身的复杂性，其损伤研究尚未形成完善的体系。

二维平纹编织C/SiC复合材料的材料属性为正交各向异性，其经向和纬向纤维损伤的相互影响很小，某一方向纤维发生部分甚至完全失效并不会影响另一方向纤维的承载能力。因此针对二维平纹编织C/SiC复合材料板结构，结合Tsai-Hill准则，参考张行的《断裂与损伤力学》给出损伤演化方程的形式[16]，引入面内3个方向相互独立的各向异性损伤演化方程：

(5)

式中：Di为面内3个方向的损伤度，下标i为x、y或xy；A、B、m和n为材料损伤参量；η为面内两方向应力之比；σth为应力门槛值；σeq为使用Tsai-Hill准则形式的等效应力，其计算式为

(6)

式中：Sx、Sy分别为材料x、y方向拉伸强度；Sxy为面内剪切强度；F12为耦合参数。

2 二次开发程序及损伤仿真计算结果分析

使用大型通用有限元分析软件ANSYS的参数化设计语言APDL，本文针对损伤分析问题进行了二次开发，对模型求解后，提取各个单元的应力代入损伤演化方程，计算并累加其损伤度，判断是否满足破坏条件(即损伤度达到1)，而后依据其损伤度对各个单元进行刚度折减，并重新加载进行求解。基本流程如图1所示。

下面使用该二次开发程序对二维编织C/SiC复合材料板结构等模型进行损伤仿真分析。

2.1 均布循环载荷下正文各向异性薄板损伤分析

本文研究的正交各向异性薄板结构的长、宽、厚的比值为253∶173∶1。假设材料制作工艺理想，基体填充密实，所用材料参数如表1所示[17]。

由于对称性，在ANSYS中建立板的四分之一模型，采用solid185单元，垂直于板面方向分为5层，共使用31 680个单元。板面周边20倍厚度范围内施加垂直于板面的位移约束(如图2所示)，中心区域施加垂直于板面的法向均布载荷，对称边界施加对称约束。图中垂直于板面为z轴方向，沿板宽度方向为x轴方向，沿板长度方向(即竖直方向)为y轴方向。

表1 正交各向异性薄板模型材料参数[17]Table 1 Material parameters of orthotropic thin plate model[17]

板正面所受x方向正应力分布结果如图3(a)所示，y方向正应力如图3(b)所示。可见，板模型所受x、y方向正应力的最大值分别发生在板受载区域的长边中心和短边中心，板上下表面应力基本相等。其中x方向正应力的最大值约为y方向正应力最大值的1.4倍。

由于C/SiC复合材料的基体属于脆性材料，导致该材料在初次受载后会产生较大的损伤[18](本文中称之为初始损伤)，因此损伤度初始值不为零，其大小由初次加载产生的应力决定。另外使用各向异性损伤演化方程式(5)，结合该材料的S-N曲线[19]进行拟合，得到损伤演化方程如下：

图2 模型及约束条件Fig.2 Model and constraint condition

图3 应力分布云图Fig.3 Stress distribution contour

(7)

将式(7)代入二次开发程序进行损伤累计，发现x方向损伤演化最快，y方向和xy剪切损伤度基本不变。损坏首先发生于板背面(不直接受载面)长边中心位置，即x方向应力最大值发生位置，而后经过较长时间板正面才发生损坏，且后续损坏扩展速度急剧提高，并由初始位置沿板长方向扩展，总体而言正面裂纹扩展速度要快于背面，损伤演化过程如图4所示。

分别提取板正反面x方向最大损伤度Dx进行对比，发现加载之初，板正反面损伤演化进程基本一致，但载荷循环周次达到约75.7×104后，损伤进程发生明显分离，板背面最大损伤度急剧上升，如图5所示。

进一步对板损坏单元的损伤度演化过程进行考察，板背面最先损坏的3个单元及正面最先损坏的几个单元的损伤度演化分别如图6所示。将破坏单元按正反面分开且按破坏顺序依次标记，图中标注“*面单元-[j]”中的“j”代表正面或反面损坏单元的损坏次序号。

图4 正交各向异性板正反表面损坏单元数Fig.4 Number of damaged units on front-side and back-side surface of orthotropic plate

另外，同样对上述单元的等效应力发展进行考察，如图7所示，发现在首个单元发生损坏后，临近单元损伤度增长遽然减缓，分析其原因，应是板背面首个单元发生损坏导致板局部刚度改变，损伤局部的应力重新分布，其等效应力下降，进而使得板正面损伤度发展减缓。

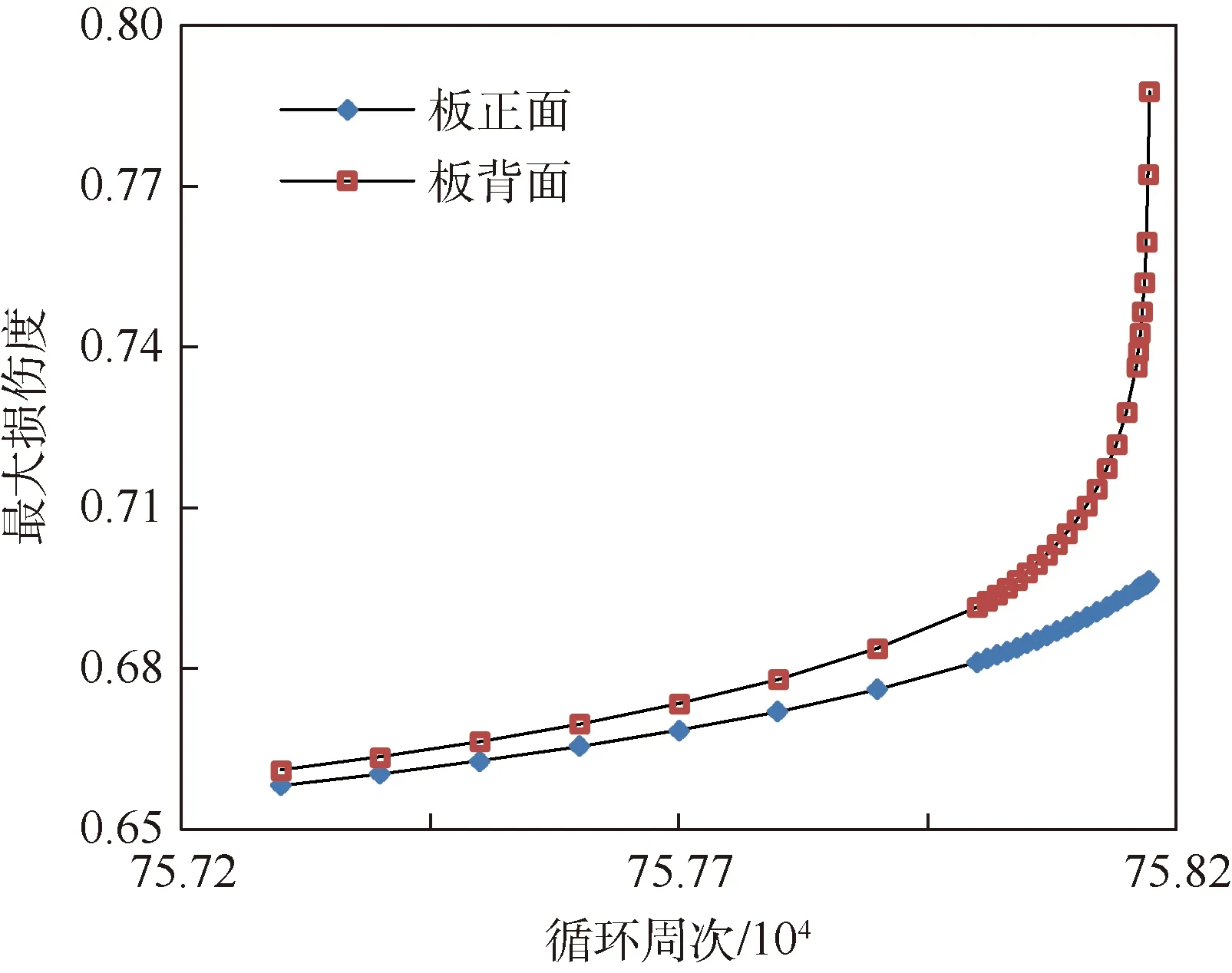
图5 正交各向异性板正反表面损伤进程分离Fig.5 Front-side and back-side surface damage evolution separation of orthotropic plate

图6 板背面单元和板正面单元损伤度Fig.6 Damage degree of plate back-side units and plate front-side units

综合对比图6和图7发现，背面第1个单元破坏前，亦即全板第1个单元破坏前，随着材料损伤累计，全板应力水平逐步下降，损伤累计急剧增长；背面第1个单元破坏后，临近区域的单元损伤演化呈现平台状，损伤累计显著减缓；同时，板正反面的临近单元等效应力显著减小。

但由于背面第1个单元破坏后，相应的板正面单元，与其他临近单元相比，损伤最大(参看图7)，其应力虽有所减小，但其损伤演化仍远快于包括背面相应单元在内的其它临近单元，因此成为全板第2个发生后继破坏的单元。

此后，特别突出的现象是，正面单元的破坏导致其同面临近单元所受等效应力水平出现跟随性阶跃增长，参看图7(b)，急剧加速了同面单元的后继破坏。这一现象往复相随，造成正面该局部出现连续性单元破坏，板整体进入加速损伤的非稳定态。

从另一角度看，单元最终的破坏也是损伤状况和应力共同作用的结果。

在正面第1个单元发生破坏前，正面第2个发生破坏的单元与背面第2个发生破坏的单元的损伤度基本一致(参看图8)，而背面第2个破坏单元的等效应力略大，因此其损伤度发展较快；但是，当正面第1个单元发生破坏时，导致正面第2个发生破坏的单元其等效应力跳跃增大(参看图9)，因此，最后阶段正面第2个单元的损伤度发展超过了背面第2个破坏的单元，并首先发生了损坏。对比图8和图9可见，等效应力保持稳定时，损伤演化较为缓慢；一旦发生单元破坏，整体应力重新分布，造成应力水平的阶跃，同时造成单元进入加速损伤的不稳定状态。

图7 板背面单元和板正面单元等效应力Fig.7 Equivalent stress of plate back-side units and plate front-side units

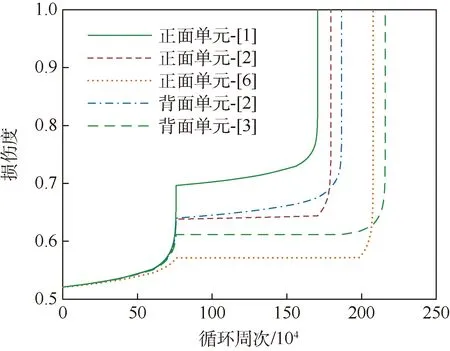
图8 板正面单元和背面单元的损伤度对比Fig.8 Comparison of damage degree between plate units of front-side and back-side

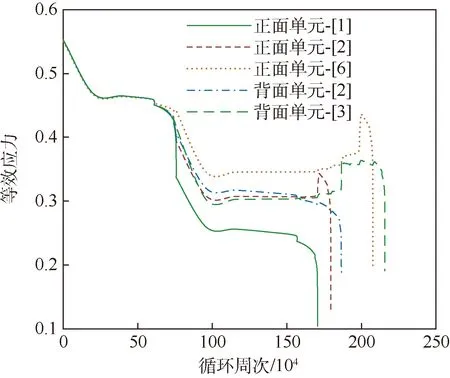
图9 板正面单元和背面单元的等效应力对比Fig.9 Comparison of equivalent stress between plate units of front-side and back-side

2.2 考虑基体沉积工艺情况的正交各向异性薄板损伤分析

实际上，平纹编织C/SiC复合材料往往采用化学气相渗透法(CVI)进行制作[20]，由于工艺原因，其成品往往上下表面基体沉积较为密实，材料性能相对较强，中间部分基体却比较疏松，材料性能较弱。一般而言，材料上下表面层与中间层的厚度之比约为1∶4。材料参数如表2所示。

在ANSYS中建立同样尺寸的具有上述中间层和表面层材料参数的三层板模型，并取四分之一模型施加同样的边界条件与载荷，其应力分布与单层材料情况十分接近，x、y方向正应力的最大值仍发生在板受载区域的长边中心或短边中心，正反面基本相等。

同样进行损伤模拟，发现x方向损伤度发展仍然最快，且损伤首先发生于板正面(受载面)受载区域长边中心，即x方向应力最大值发生位置。正面裂纹半长发展到一定长度后，板背面才开始开裂，且板中间层随后也开始迅速开裂，如图10所示。

本例中最初的损伤单元都发生在板正面；中间层由于材料性质很弱，当上下表面层单元发生破坏后，几乎失去承载能力，同时发生破坏。由于沉积工艺问题，材料的整体性产生很大不同，相比于均匀理想沉积的情况，本例中板的疲劳寿命有极大弱化，损伤演化过程也有很大不同，单元破坏数与加载周次呈现良好的线性关系，体现出材料脆性破坏的典型特征。

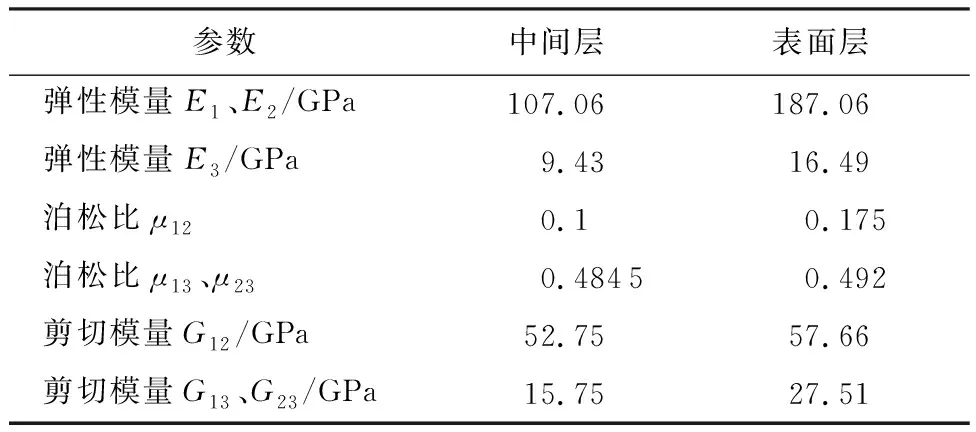
表2 正交各向异性薄板中间层和表面层材料参数Table 2 Material parameters of middle layer and surface layer in anisotropic thin plate

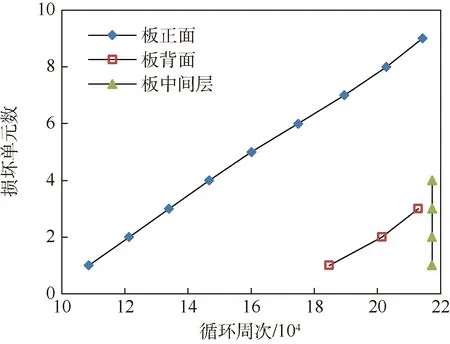
图10 正交各向异性三层板损坏单元数Fig.10 Number of damaged units of orthotropic three-layer plate model

3 损伤演化方程建立及损伤演化仿真

第1节中所述的等效应力变程是基于Tsai-Hill准则形式的无量纲量，从损伤演化方程中损伤驱动力具有的应变能性质考虑，其物理性质并不适当。另外，采用等效应力作为损伤驱动力主项，其对应的损伤度应为材料的综合损伤度，材料损伤的各向异性应表现为宏观裂纹的扩展，因此，将等效应力定义修改为如下形式：

(8)

将式(8)代入损伤驱动力方程，得

(9)

由此得到材料受脉动循环载荷的材料，其损伤演化方程形式仍如式(2)所示。

由材料S-N曲线对上述参数进行拟合，得到基于新的等效应力公式的等效损伤演化方程。

为验证上述损伤演化方程对于损伤各向异性演化描述的适用性，使用正方形板的四分之一模型，保证板x和y方向的受力状态对称，在不同的x和y方向强度条件下进行损伤模拟分析，损伤扩展云图结果如图11所示。

可以看到，在x和y方向受力对称的情况下，x方向材料强度不变，当y方向材料强度较小时，在y方向应力最大处先发生单元损坏，且后续损坏沿x方向扩展，即由y方向应力主导损伤演化；当y方向材料强度增大时，除了发生上述损伤演化，在x方向应力最大处也会发生较为明显的损伤演化，并沿y方向后继扩展。

上述现象说明，式(9)所定义的损伤驱动力由于考虑到材料各向的强度不同，在常规损伤演化方程式(2)所描述的损伤演化中，较好地揭示由于材料各向异性，特别是材料强度各向不同，所造成的材料损伤演化的各向异性。进一步，损伤驱动力是损伤演化的主导因素，损伤驱动力的“各向异性”在很大程度上直接决定了宏观损伤演化的各向异性，本文提出的损伤驱动力比较好地容纳和体现了损伤演化各向异性的内在动因，因此，损伤演化仿真结果也较为合理。

图11 正方形板不同强度条件下损伤扩展云图Fig.11 Damage extension contour of square plate under different strength conditions

4 结 论

1) 材料或结构的损伤，是由损伤驱动力主导的，同时受材料强度和应力状态影响。因此无论材料是各向同性还是各向异性，损伤一旦发生，损伤驱动力中的主要应力成分仍将对后继损伤演化产生决定性作用，所以损伤的发展必然是各向异性的。

2) 在复杂应力状态下，损伤演化的基本状况仍然如上所述。对于各向异性材料而言，材料的基本特征首先体现在材料模量的各向异性，同时，也反映在材料各方向强度的不同上。但就损伤演化而言，材料强度的不同对材料各向异性演化将起到更重要的作用。

3) 基于对正交各向异性复合材料的损伤分析的结果，提出了式(9)所定义的损伤驱动力，用以反映主要应力成分及材料强度对损伤演化的作用，从而揭示损伤演化在损伤驱动力的影响下所必然呈现的各向异性特征。

4) 受限于相关实验基础的欠缺，提出的如式(8)、式(9)和式(2)所构成的损伤演化描述体系尚有待通过实践进一步验证和改进。但本文基于损伤力学理论，根据材料标准试样疲劳S-N曲线确定损伤演化方程参数，进行了定性模拟分析，具有理论严谨性和一定的实验基础。通过本文损伤模拟的结果，说明损伤演化方程具有基本的理论合理性和与基本损伤演化认识的一致性。