成分数据的空间自回归模型

黄婷婷， 王惠文， SAPORTA Gilbert

(1. 北京航空航天大学 经济与管理学院, 北京 100083； 2. 城市运行应急保障模拟技术北京市重点实验室， 北京 100083；3. 北京航空航天大学 大数据科学与脑机智能高精尖创新中心， 北京 100083；4. 法国国立工艺学院 计算机和通信研究中心, 巴黎 75003)

数据搜集技术的快速发展不仅带来了海量的数据，也带来了类型越来越复杂的数据，如函数数据[1-3]、成分数据[4]和符号数据[5-6]等。在这些类型复杂的数据中，成分数据由于关注部分在总体中的占比信息，受到愈来愈广泛的关注。如Fry等[7]利用住户开支统计调查结果研究预算分配模型，Pawlowsky-Glahn和Egozcue[8]利用成分数据比较东欧和西欧国家在食物消费结构上的习惯差异，Pawlowsky-Glahn[9]等利用成分数据回归模型分析了巴西宗教信仰构成的变化。

成分数据分析主要研究活动对象结构变化产生的规律及其对其他对象产生的影响。关于成分数据的理论研究，标志性的成果是1986年Aichison撰写的《成分数据统计分析》[10]，该书详细阐述了成分数据统计分析方法建立的数学基础。在成分数据分析中，线性回归模型是一种常用的分析技术。现有的成分数据线性回归模型可以分为两大类：第1类因变量是普通数据[11-12]，第2类因变量是成分数据[13-15]。Hron等[12]利用第1类成分数据线性回归模型研究了GDP组成与预期寿命的关系；而Wang等[14]利用第2类模型研究了地区总产值与就业和投资的关系。本文在因变量是普通数据的成分数据回归模型基础上进行研究。在成分数据回归模型中，通常以样本之间独立同分布作为前提。而在实际应用中，独立同分布的假设往往是不成立的。如何对现有的成分数据线性回归模型进行改进，使之适应实际应用的需求，是一个值得深入研究的问题。

在空间计量经济学[16]中，空间自回归模型通过引入空间依赖项，打破了因变量相互独立的假设，使得许多与空间地理位置或社交网络有关的现象得到解释。利用空间自回归模型，可以对区域经济发展的问题[17-18]、溢出性问题[19-20]等进行分析。现有的空间自回归模型在普通数据的基础上已经发展得相对完善，已有的对空间自回归模型进行估计的方法包括Ord[21]和Lee[22]提出的极大似然估计法、Kelejian、Prucha[23]和Lee[24]提出的广义矩估计法、Lesage和Pace[25]从贝叶斯的角度提出的马尔可夫链蒙特卡罗方法(Markov chain Monte Carlo method)。

因此，针对经典成分数据线性回归模型假设样本间相互独立的严格要求，研究因变量之间具有空间依赖的成分数据回归模型，通过在普通数据的空间自回归模型中，引入成分数据的协变量，提出了同时含有成分数据和普通数据的空间自回归模型。并依据成分数据的特点，给出了混合2种数据的空间自回归模型的估计方法。提出的新模型比已有的成分数据线性回归模型具有更强的灵活性，可以处理更加复杂的空间依赖问题。

1 基础理论

本节主要介绍成分数据的代数空间——单形空间(simplex)中的基本运算，以及与成分数据联系紧密的几种变换，利用这些变换可以将具有约束的成分数据转化成易于处理的普通数据。

1.1 单形空间

对于含有d个成分的成分数据，对应的单形空间Sd(上标d表示成分数据有d个成分，因此实际是d-1维的)定义为

Sd={x=(x1,x2,…,xd)T,

(1)

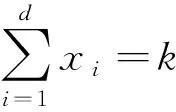
现有单形空间Sd中的任意2个成分数据x、y以及实数α，记x=(x1,x2,…,xd)T∈Sd，y=(y1,y2,…,yd)T∈Sd，α∈R，则x和y的加法⊕及α和x数乘运算⊙可分别定义为

x⊕y=C(x1y1,x2y2,…,xdyd)

(2)

(3)

式中：C(·)表示闭合运算，定义为

(4)

不难看出，闭合运算保证了运算结果仍在Sd中。基于运算⊕和⊙，可以导出x和y的减法运算，

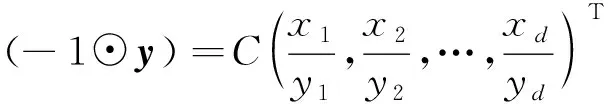
(5)

x和y的内积运算〈x,y〉a定义为

(6)

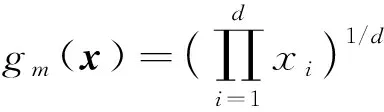
(7)

(8)

可以证明，含有内积运算的单形空间是一个希尔伯特空间。

1.2 等距对数比变换

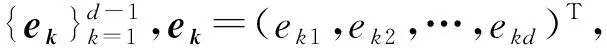
ilr(x)=(〈x,e1〉a,〈x,e2〉a,…,〈x,ed-1〉a)T

(9)

Egozcue等[26]证明，ilr变换是保内积的变换，即对于含有d个成分的成分数据x和y,有

〈x,y〉a=〈ilr(x),ilr(y)〉

(10)

下面给出具体的ilr变换过程。

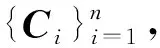
ξi=ilr(Ci)=clr(Ci)ΨT=ln(Ci)ΨT

(11)

式中：

clr(Ci)=

Ψ为(d-1)×d维的矩阵，具体表达式为

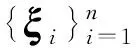
2 模型的提出

Y=ατn+ρWY+〈C,B〉a+XΓ+E

(12)

式中：ατn为截距项，τn为所有元素均为的1的维度为n的向量；ρ为未知的空间自相关参数，取值在区间(-1,1)内；W={wij}n×n为外生的空间矩阵，wij为对象i与j之间的权重；B为待估的成分数据系数，具有p个成分；Γ为普通数据的待估系数；E为独立于X的误差项，服从均值为0，方差为σ2In多元正态分布，In为n×n的单位矩阵。

需强调的是，式(12)中C和回归系数B都为成分数据，〈C,B〉a为一个实数。在Aitchison内积空间中，〈C,B〉a代表X对Y解释性最强的投影方向。

当ρ=0时，式(12)退化为普通的成分数据线性模型。在这个意义上，式(12)比经典的成分数据线性模型具有更强的灵活性，可以处理更加复杂的数据关系。

3 估计方法

为估计模型式(12)中的参数α,ρ,B,Γ，首先需将相互不独立的成分数据转化为相互独立的普通数据，1.2节中已作详细介绍；其次，要解决因变量yi之间不相互独立的问题，此处采用极大似然估计法ilr变换后的模型进行估计。

同样利用1.2节中的ilr变换，可得到成分数据系数B的变换坐标b=ilr(B)。

由于B是需估计的参数，因此变换后的坐标b是未知的。记ξ=(ξ1,ξ2,…,ξn)T，则模型式(12)可写为

Y=ατn+ρWY+ξb+XΓ+E

(13)

为描述简便，记：δ=(b,Γ)T，Z=(ξ,X)，则式(13)可表示为

Y=ατn+ρWY+Zδ+E

(14)

由于模型式(12)中误差项服从多元正态分布，因变量Y的似然函数为

(15)

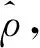
(16)

(Y-ατn-ρWY-Zδ)

(17)

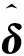
(18)

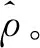
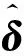
(19)

至此，所有参数都可以估计出来。

4 数值模拟

为评估所提出估计方法的统计性质，下面设计了几组数值模拟实验检验估计量的表现。所有的计算过程都是在R软件中实现，用到的包有“spdep”和“compositions”。

关于空间自回归模型的空间网络结构，采取最常见的“车”相邻(rook matrix)。假设n个样本点随机地散落在一个R行T列的格子棋盘上，每个样本点占据棋盘上的一个方格，那么在棋盘上共享一条边的2个样本点就是相邻的。在这样的情况下，处在棋盘中间的任意样本点都有4个邻居，处在棋盘边上的样本点有3个邻居，而处在棋盘角上的样本点只有1个邻居。分别设置R=10，20，30，T=30，25，30，相应地样本量n=R×T=300,500,900。为了查看空间依赖的强弱是否对估计量有影响，同样设计了3组不同的ρ值，ρ=0，0.5，0.8。

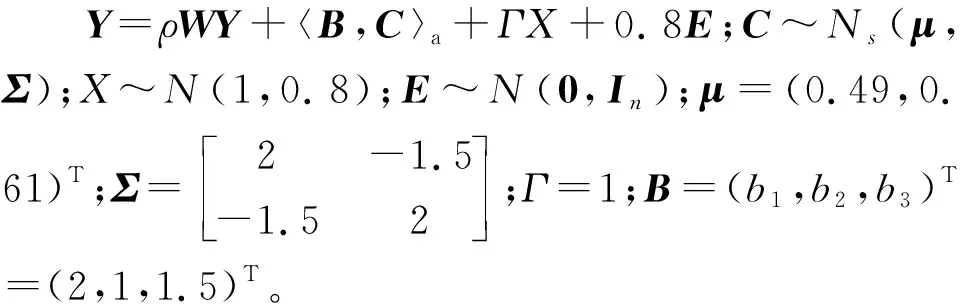
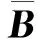
(20)

样本的总方差的计算公式为

(21)

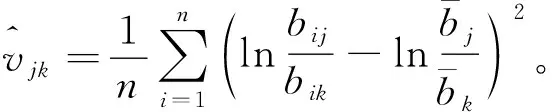
估计结果如图1～图3所示。可以得到如下结论：

图和的样本偏差Fig.1 Sample deviation of

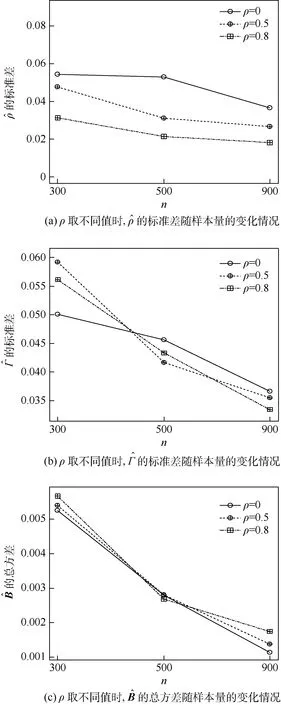
图的标准差及的总方差Fig.2 Standard deviation of and

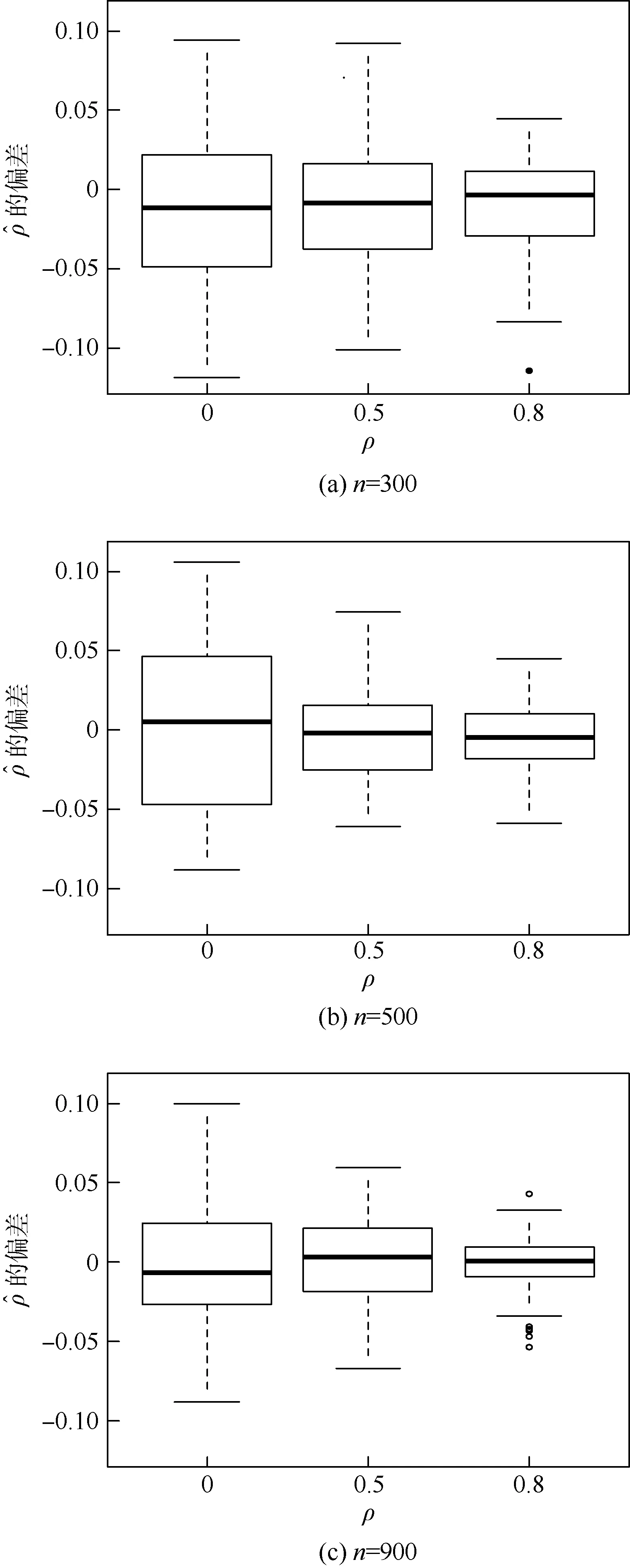
图3 n和ρ取不同值时，偏差箱线图Fig.3 Boxplots of deviation of when n and ρ change

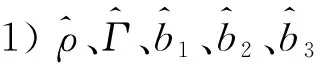
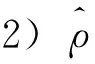
5 结 论

针对普通成分数据线性回归模型要求样本间相互独立的局限性，在空间自回归模型的基础上，提出了混合成分数据与普通数据的空间自回归模型，所提出的模型及估计方法具有如下优点：

1) 新提出的模型不仅能够同时处理成分数据和普通数据，还能表达数据中因变量之间相互依赖的问题。特别地，新模型可以处理地理空间中的依赖性。

2) 新模型所提出的估计量具有相合性。随着样本量的增大，可以发现估计值的标准差在逐渐减小。除此之外，新提出的估计方法操作简单，可以在R软件上直接实现。

在实际应用中，新模型可处理社交网络、地理空间等含有网络结构的依赖问题。而针对其他情况造成成分数据线性模型样本之间不相互独立的问题，则需要分情况进行深入分析。