在习题教学中培养学生的高阶思维能力
吴 刚
(巴中市恩阳区恩阳中学,四川 巴中 636064))
高阶思维是基于“复杂情境”问题分析而得到的“机制”和“结晶”[1].思维由低到高分为记忆、理解、应用、分析、评价和创造六个层级,其中前三个层级为低阶思维;后三个层级为高阶思维[2].低阶思维是发展高阶思维的基础,高阶思维是低阶思维进入深度学习区后表现出来具有更高水平的思维过程和成果.在习题评讲教学环节有意识地通过“一题多解”、“一题多变”、“数理结合”和“反思质疑”,把问题情境适当延宽一些,把思维触觉适度拓深一些,促进学生对问题情境有更深入的理解、对物理过程有更透彻的分析,达到培养学生高阶思维的能力和发展学生核心素养的目标.
1 一题多解
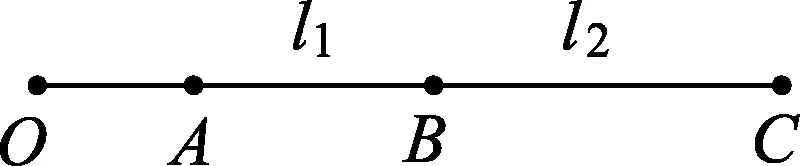
图1
例1.已知O、A、B、C为同一直线上的四点,A、B间的距离为l1,B、C间的距离为l2,如图1所示.一物体自O点由静止出发,沿此直线做匀加速直线运动,依次经过A、B、C三点.已知物体通过AB段与BC段所用的时间相等,求O与A的距离.
设物体的加速度为a,经OA段的时间为t0,物体经AB段和BC段的时间均为t,O与A的距离为l,对物体经过OA段、OB段、OC段分别有
(1)
(2)
(3)
(4)
(5)
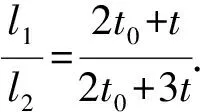
(6)
(7)
设物体在A点的速度为vA,则有
(1)
l1+l2=2vAt+2at2.
(2)
由(1)、(2)式得
l2-l1=at2.
(3)
3l1-l2=2vAt.
(4)
设O、A间的距离为l,则有
(5)
由(3)~(5)式联立解得
解法3:利用v2=2as和v2=v02求解.
设A、B、C三点的速度分别为vA、vB、vC,则有
vA2=2al.
(1)
vB2-vA2=2al1.
(2)
vC2-vB2=2al2.
(3)

(4)
解法4:利用Δs=aT2求解.
由题意有l2-l1=at2.
(1)
(2)
vB2=2a(l+l1).
(3)
由(1)~(3)式联立解得
解法5:利用v-t图像求解.
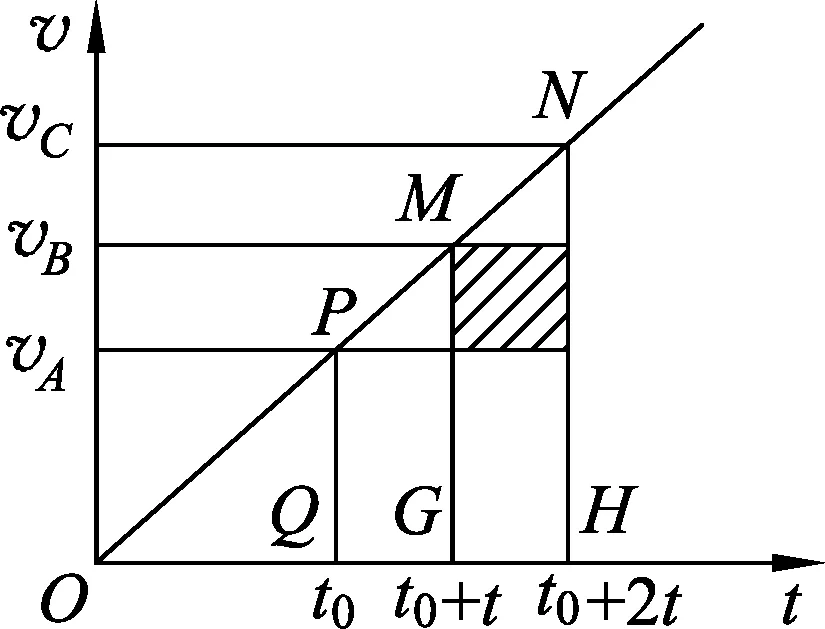
图2
作出物体从O到C的v-t图像,如图2所示.设t0、t0+t、t0+2t时刻物体分别通过A、B、C3点,速度分别为vA、vB、vC.
由图中“面积”的物理意义及三角形相似比(△OPQ∽△OMG)得
(1)
BC段比AB段多通过的位移可表示为(阴影面积)
l2-l1=(vB-vC)t.
(2)
梯形PNHQ的面积是AC段的位移,则有
l1+l2=vB·2t.
(3)
本题看似一道极常规的试题,却隐含着重重思维障碍,对学生解方程组的数学能力要求极高.在解法1中,有效方程数少于未知量数,学生因缺乏计算技巧而不知如何联立求解出最后结果.在解法2中,由(1)、(2)式得出(3)、(4)式,然后计算出A点速度,计算方法巧妙,学生很难想到.解法4则回避了这一难点,更显灵活.通过“一题多解”,有助于培养学生对同一问题从多维角度分析、思考,开阔学生思路,达到发展学生的发散思维.
2 一题多变

图3
例2.如图3所示,已知电源电动势为6 V,内阻为1 Ω,保护电阻R0=0.5 Ω.求:当电阻箱R读数为多少时,保护电阻R0消耗的电功率最大,并求这个最大值.
解析:保护电阻R0消耗的功率为
因R0和r是常量,而R是变量,所以R最小时,P0最大,即R=0时,
变式1.在其他条件不变的条件下,当电阻箱R读数为多少时,电阻箱R消耗的电功率PR最大,并求这个最大值.
解析:电阻箱R消耗的电功率为

变式2.在例题中,若电阻箱R的最大值为3 Ω,R0=5 Ω,求:当电阻箱R读数为多少时,电阻箱R的电功率最大,并求这个最大值.
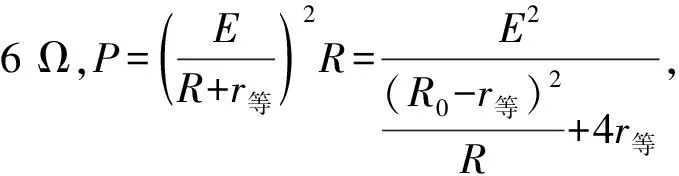
变式3.例题中条件不变,求电源的最大输出功率.
解析:由
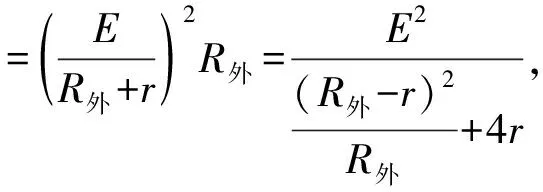
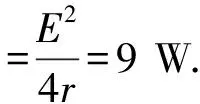

图4
变式4.如图4所示,电源电动势E=2 V,内阻r=1 Ω,电阻R0=2 Ω,可变电阻的阻值范围为0~10 Ω.求:可变电阻为多大时,R消耗的功率最大,最大值为多少?

根据闭合电路欧姆定律,路端电压为
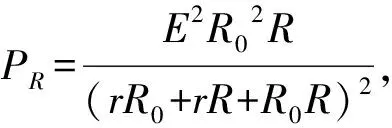
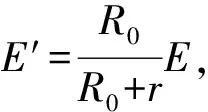

通过改变题目的条件或要求,对各种情况下功率的分析计算,使学生对知识的理解和应用能做到举一反三、触类旁通,起到“做好一题、带活一片”的效果,对培养学生发散、创新思维能力大有裨益.
3 数理结合
例3.用轻绳悬挂一小球将小球拉至水平位置.然后放手使小球由静止开始向下摆动,在小球摆至最低点的过程中重力对小球做功的功率
(A) 保持不变. (B) 不断变大.
(C) 不断变小. (D) 先变大后变小.
解析:这是一道高一物理必修2学习到瞬时功率计算时常考的题,一般用极限方法求解.小球在初位置速度为0,在最低点重力与速度垂直.由P=Fvcosα可知,小球在初、末位置重力的瞬时功率均为0,而在中间过程功率不是0.所以排除(A)、(B)、(C).下面对这个情景做一些深入定量分析,用于研究性学习,发展学生的高阶思维能力.
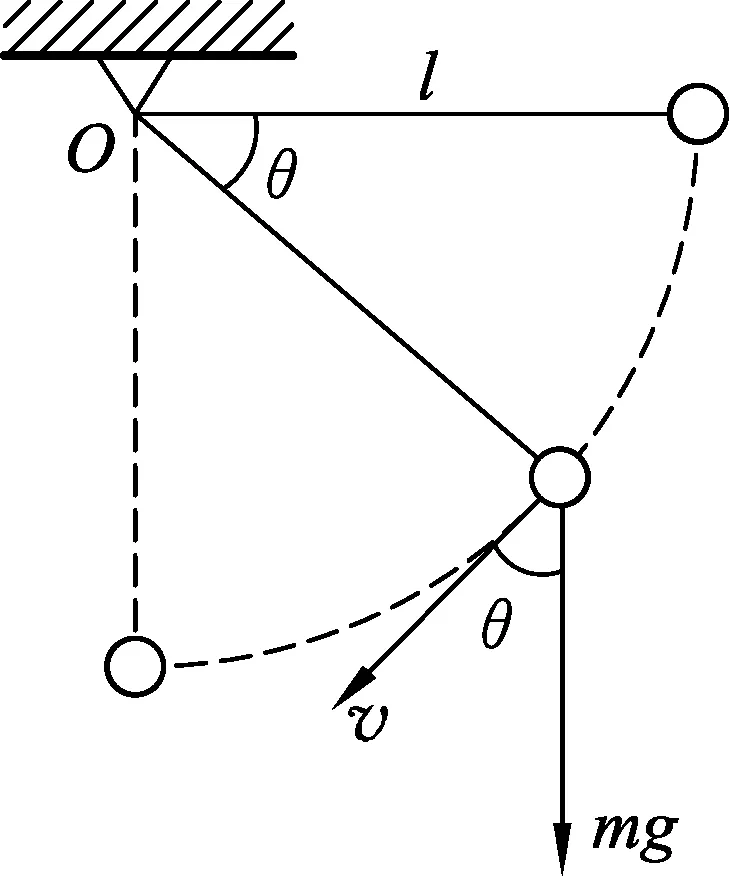
图5
一般我们习惯从时间或空间维度观察物理量的变化,即找到物理量随时间变化的函数或随位置坐标变化的函数.本情景中重力功率随时间的关系很难找,但随空间的关系比较容易找.如图5所示,设摆长l、摆球质量m为定值,空间位置可用θ确定,找到重力的功率和θ的关系即可.

(1)
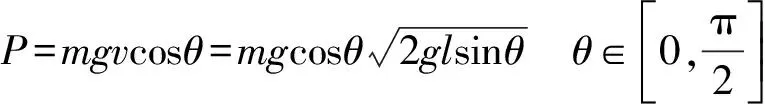
(2)
为看出P(θ)函数单调性,将上式整理得

方法1:通过求导讨论单调性.
φ′(θ)=cosθ·cos2θ-2sin2θcosθ=3cos3θ-2cosθ.


利用作图软件作出φ′(θ)=3cos3θ-2cosθ的图像,如图6所示.

图6

故φ(θ)=sinθ·cos2θ在θ≈35°有极大值,即重力的功率先变大后变小.
方法2:通过换元将三角函数转化为多项式来讨论单调性.
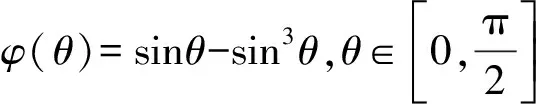

图7
由图像可看出θ≈35°时,φ(θ)=sinθ·cos2θ有极大值,同理得到重力的功率先变大后变小.
4 反思质疑

图8
例4.木板向右水平运动时,上面轻放一木块,如图8所示.木块与木板、木板与地面均不光滑.最大静摩擦力近似等于滑动摩擦力,木块和木板质量相等.木块始终在木板上,则放上木块后木板的v-t图像正确的是


图9
该学生选出的答案固然是正确的,但是解答过程并不完整.这道题涉及的物理过程还是比较复杂的,需要分情况讨论,才能做出正确的解答.

图10
解析:两者一起匀减速直线运动是有条件的,有可能木块不能和木板一起做匀减速直线运动.下面进行分析讨论:设木板上下表面的动摩擦因数分别为μ1、μ2.两者有相对运动时,对木块:a块=μ1g,对木板:a板=μ1g+2μ2g,a块 图11 图12 若μ1≤μ2,共速后两者不可能相对静止.通过分析可知,只能出现木块相对木板向前运动的情况,即木块受到与木板速度相反的滑动摩擦力作用,继续减速,木块和木板受力分析如图11所示.对木块有,a块′=μ1g,对木板有,a板′=2μ2g-μ1g,由于a块′=a块 好多学生在做选择题时,只求选出符合题意要求的选项,但有时其思维过程是不完整的,甚至是错误的.把学生在解答过程中存在的思维障碍暴露出来并加以剖析,让学生对问题给予充分的质疑、辩论,以便能更好地培养学生严谨的学科思维和发展核心素养.