基于时间序列与横截面数据的吉林省水稻产量预测对比分析*

陈 威，祁伟彦，袁福香，李哲敏※

（1. 中国农业科学院农业信息研究所，北京100081；2. 吉林省气象科学研究所，长春130062）

0 引言

水稻是世界三大粮食作物之一，是我国最主要的粮食作物，全国65%以上的人口以稻米为主食。我国水稻播种面积占全国粮食播种面积的27%左右，产量占全国粮食总产量的37%左右［1］。因此，水稻的稳产增产以及对水稻产量的准确预测对我国农业政策调整和保障我国粮食安全问题具有重要意义。

国内学者在粮食产量预测方面做了大量研究，有的利用粮食产量的时间序列数据进行预测，有的利用与粮食生产密切相关的多重参数的横截面数据进行预测。时间序列数据预测常用的预测算法有自回归滑动平均、人工神经网络等。由于时间序列预测只需变量本身的历史数据，不需要其他参数的数据，模型构建较为简单，因此在粮食产量预测中应用十分广泛。然而，时间序列预测假设粮食产量具有线性变化的规律，但粮食生产具有受多维度因素影响的复杂性，使其呈现非线性变化。因此，单纯采用时间序列的方法进行粮食产量预测，预测精度不高。横截面数据预测常用的方法有支持向量回归、神经网络等。在利用横截面数据进行粮食产量预测以及支持向量回归构建模型时参数一般依靠经验来确定，而神经网络训练模型对网络初始权重高度敏感，且对训练集样本的依赖性强，因此预测结果有时并不理想。

水稻产量受自然因素、生产技术因素、社会经济因素和随机因素等多因素影响，是线形关系和非线性关系并存的复杂性问题。使用单一模型进行水稻产量预测，当影响产量的重要因素发生变化时可能导致预测结果的不稳定。为了对比不同模型预测效果，分析各模型预测水稻产量的特点、不足及适用条件，为粮食产量预测问题模型选择提供依据，该研究从时间序列预测和横截面数据预测两种角度，选取4种模型对水稻产量进行预测。在时间序列预测方面，依据吉林省水稻产量的历史数据，基于自回归滑动平均（Autoregressive Integrated Moving Average Model，ARIMA）模型和长短期记忆人工神经网络（Long-Short Term Memory，LSTM）模型进行吉林省水稻产量预测。ARIMA模型在粮食产量预测中应用广泛［2-3］，而LSTM模型属于反馈神经网络的范畴，在时间序列的学习和处理上有独特优势，在语音及图像识别、机器翻译等方面已有较多研究［4-6］，但在粮食产量预测中应用较少［7］。由于农作物生长产生过程中动物害虫和病原体的侵害可引起显著的产量潜在损失［8-9］，竞争性作物品种种植面积对水稻的产量也有重要影响，因此选取吉林省重要病虫害发生情况、玉米和大豆种植面积产量等历史数据作为横截面数据预测的原始数据。在横截面数据预测模型选择上，选取支持向量回归模型和多层感知器模型进行预测。支持向量回归模型在解决小样本问题中具有优势，已有学者采用此模型进行农作物产量的预测［10］，而多层感知器模型作为最简单的神经网络模型，具有良好的容错性和自适性，可有效处理非线性可分离问题，在语音识别、机器翻译等方面已有大量研究［11-13］，用于粮食产量预测的报道不多。

1 模型简介

1.1 自回归积分滑动平均（ARIMA）模型

ARIMA模型全称为自回归积分滑动平均模型，是指将非平稳时间序列转化为平稳时间序列，然后将因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型。ARIMA模型的3个参数为p、d、q，其中p代表预测模型中采用的时序数据本身的滞后数，也叫做自回归项数，d代表时间序列成为平稳时所作的差分次数，q代表预测模型中采用的预测误差的滞后数，也叫做移动平均项数［14］。

1.2 长短期记忆人工神经网络（LSTM）模型

长短期记忆人工神经网络是一种改进的循环神经网络（Recurrent Neural Network，RNN），避免了传统RNN隐含层层数过多计算量庞大而产生的梯度消失和梯度爆炸的问题。LSTM的经典结构如图1所示，Cell是计算节点的核心，通过遗忘阀门（forget gate）、输入阀门（input gate）和输出阀门（output gate）的打开或者关闭来判断模型网络的记忆态（之前网络的状态）在该层输出的结果是否达到阈值，从而加入到当前该层的计算中［15］。

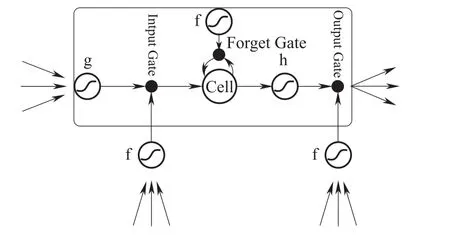
图1 长短期记忆人工神经网络（LSTM）模型结构Fig.1 Model structure of LSTM（Long-Short Term Memory）

1.3 支持向量回归（SVR）

支持向量机（Support Vector Machine，SVM）是机器学习领域中基于统计学习理论的分类回归方法，由AT&T贝尔实验室的Vanpnik于20世纪90年代提出，通过构造核函数将原空间非线性问题转换成高维空间的线性问题，可以成功处理分离问题，辨别分析回归问题等［16］。在处理分类问题时，支持向量机相当于找到一个高维特征平面，使两个分类集合的支持向量或者所有数据离分类平面最远，而支持向量回归（Support Vector Regression，SVR）则是找到一个高维回归平面，使一个集合中的所有数据到该平面的距离最近。

1.4 多层感知器MLP模型

MLP（Multilayer Perceptron，MLR），即多层感知器，是一种常见的神经网络模型，由输入层、隐藏层和输出层组成，其基本结构如图2所示。MLP是一种监督学习模型，在模型训练过程中，不断提供完整的输入和输出，模型基于一定长度的历史数据不断训练、学习，从而构建出输入和期望的输出之间的最优模型，而后利用得出的最优模型进行预测［17］。

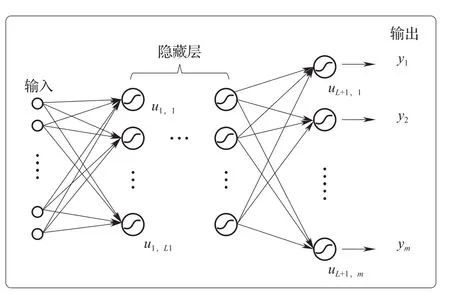
图2 多层感知器（MLP）基本结构Fig.2 Basic structure of MLP（Multilayer Perceptron）

2 水稻产量预测实证分析

2.1 数据来源

研究中所用到的实验数据为1949—2015年吉林省玉米、大豆及水稻的种植面积、单产及总产量数据，以上数据来自吉林省统计局；吉林省稻瘟病发病频率（1961—2009年）、玉米螟发生情况（1980—2007年）、地下害虫及大豆蚜发生情况（1981—2006年）、食心虫发病情况（1982—2006年）、黏虫发生情况（1979—2006年），以上数据来自吉林省气象局。

以1990年为基期，1990年之前的数据作为训练集数据用于模型训练，1990年之后的数据作为预测集数据，用于检测模型预测效果。

2.2 评价指标

使用均方根误差值（Root Mean Square Error，RMSE）作为评价指标对各模型模拟效果进行评价和比较。RMSE是观测值与真值偏差的平方和观测次数n比值的平方根，计算方法见公式（1）。RMSE值越小，表明预测值与拟合值之间偏差越小，预测性能越好，反之则预测性能越差。

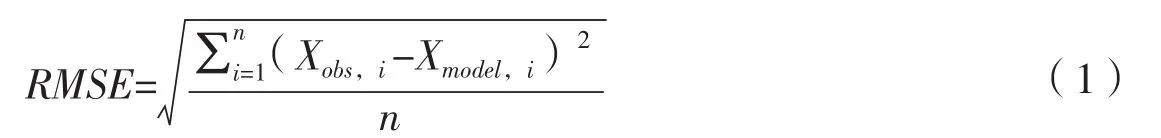
2.3 从时间序列角度预测产量

（1）基于ARIMA的时间序列预测

①时间序列平稳性检验及平稳化处理

导入吉林省1949—1990年历年水稻总产量原始数据，并检验时间序列的稳定性。若时间序列的统计学特性（例如均值、方差）随时间保持不变，则认为该序列是平稳的。

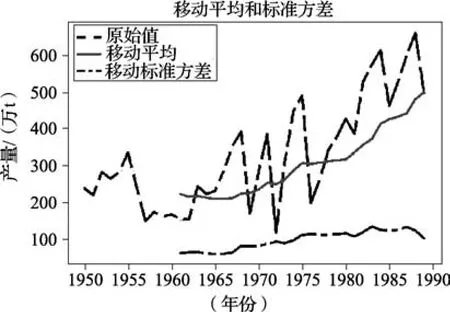
图3 1950—1990年吉林省水稻总产量Fig.3 Total rice yield in Jilin province from 1950 to 1990

如图3所示，1949—1990年吉林省水稻总产量呈上升趋势，年增长幅度不同。由移动平均值和移动标准方差曲线可以看出，移动标准方差随时间变化较小，但移动平均值随时间呈明显的上升趋势，因此该序列不是平稳序列，需要进行平稳化处理。

由于原数据值域范围比较大，为了缩小值域，同时保留其他信息，对原始数据进行对数转换，之后采用差分的方法，将每一年的数值与滞后10年的值作差，去除数据的趋势性（图4）。

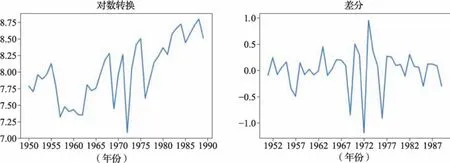
图4 原始数据平稳化处理Fig.4 Stationary process of raw data

经对数转换和差分处理后，数据的移动均值和移动标准方差在时间轴上振幅明显缩小，DFtest结果显示Test Statistic的值小于Critical Value（1%）的值，表明在99%的置信度下，该时间序列数据是稳定的，如图5。

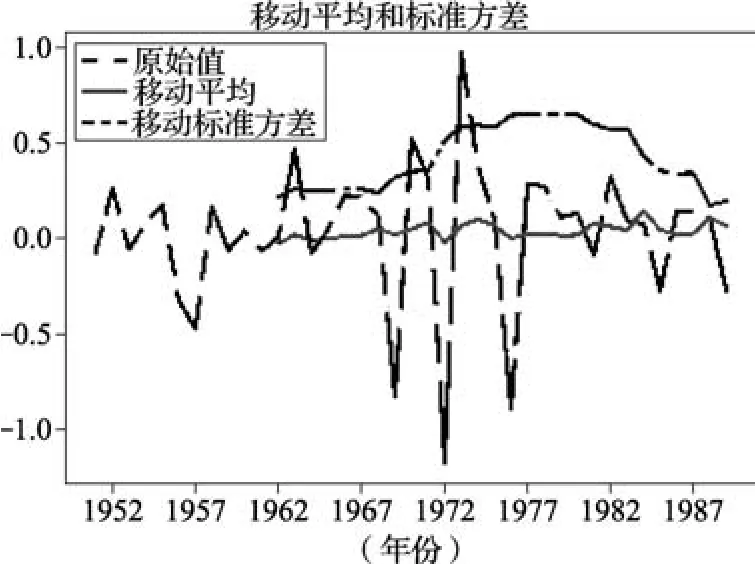
图5 平稳化处理后移动均值与移动标准方差曲线Fig.5 Rolling mean and standard deviation after stationary process

②构建ARIMA模型

通过自相关函数（ACF）和部分自相关函数（PACF）进行ARIMA（p，d，q）的p，q参数估计。由前文差分部分已知，原始数据经一阶差分后数据已经稳定，可得到d=1。所以用一阶差分化的Y’t=Yt-Yt-1作为输入。画出ACF，PACF的图像（图6）。

图6中，上下两条灰线之间为置信区间，p的值为ACF第一次穿过上置信区间时的横轴值。q的值为PACF第一次穿过上置信区间的横轴值。所以从图6可以得到p=2，q=2。由此，可生成模型ARIMA（2，1，2）。

取AR模 型（ARIMA（2，1，0））、MA模 型（ARIMA（0，1，2））、ARIMA模 型（ARIMA（2，1，2））这3种参数取值的3个模型与稳定化处理后的输入数据进行拟合，比较RSS值得出，ARIMA模型（ARIMA（2，1，2））拟合度最好（图7）。

③ARIMA模型预测

对ARIMA模型（ARIMA（2，1，2））拟合值进行差分和对数处理的逆运算（图8a），使拟合值回到原始区间，并利用该模型对1991—2015年水稻产量进行预测（图8b）。

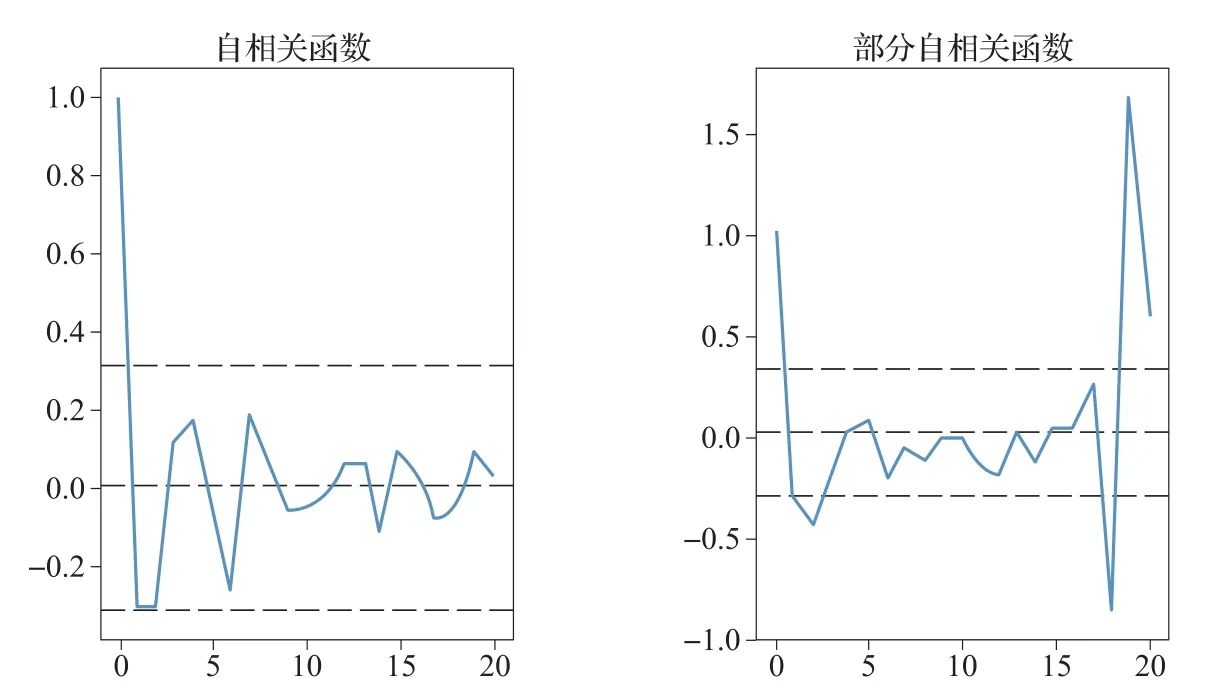
图6 自相关函数（ACF）和部分自相关函数（PACF）曲线Fig.6 Curve graph of ACF and PACF

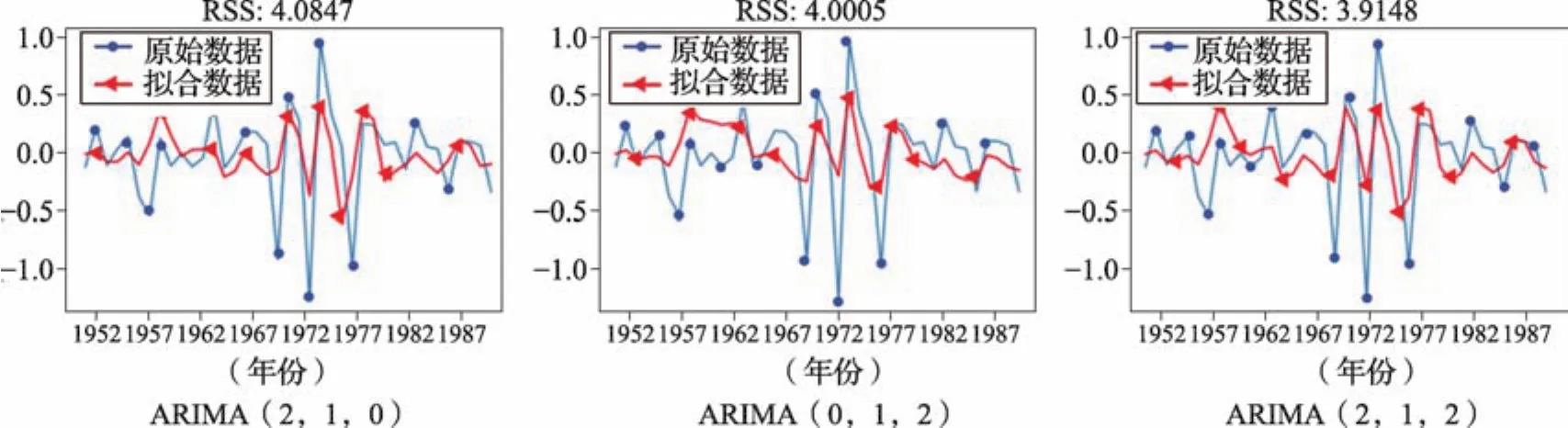
图7 3种参数ARIMA模型与平稳数据拟合度分析Fig.7 Fitting analysis of three parameters ARIMA model with stationary data

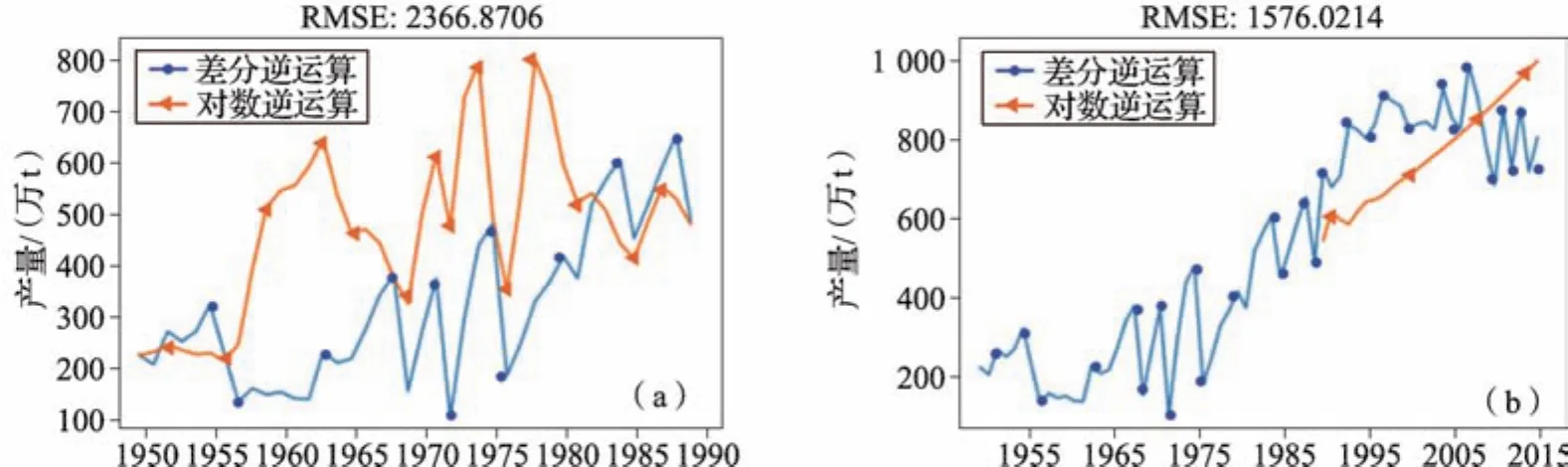
图8 差分与对数的逆运算（a）及水稻产量预测（b）Fig.8 Inverse operation of difference and logarithm（a）and yield prediction of rice（b）

1949—2015年吉林省水稻产量整体呈上升趋势，期间由于气候因素和政策导向等导致一些年份水稻产量出现较大波动，特别是2005—2015年。ARIMA模型预测结果较好地反映了水稻产量整体上升的趋势，但对原始数序列的波动没有做出反应。

（2）基于LSTM的时间序列预测

①建立模型

使用Keras深度学习库在Python中构建LSTM网络模型。参数设置为默认参数，即输入层有1个input，隐藏层4个神经元，输出层为预测一个值，激活函数用sigmoid，迭代100次，batch size 为1。利用上面得到的平稳序列数据对模型进行训练。

②模型预测

利用得到的LSTM模型对1991—2015年水稻总产量进行预测，结果如图9。

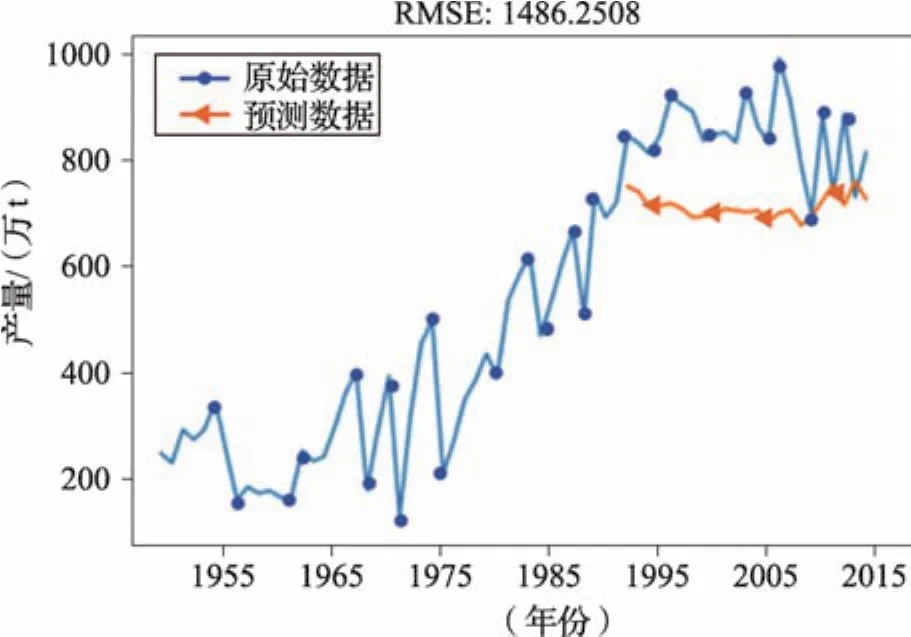
图9 长短期记忆人工神经网络（LSTM）模型预测水稻产量Fig.9 Prediction of rice yield using LSTM model

可以看出，LSTM模型较预测曲线整体趋势较为平缓，预测产量普遍低于实际产量，未能反应水稻产量整体上升的总体趋势，对于原始数序列的波动反应不明显。

2.4 从横截面数据角度预测产量

实验中用于预测水稻产量的病虫害数据为吉林省历年稻瘟病发病频率（1961—2009年）、玉米螟发生情况（1980—2007年）、地下害虫及大豆蚜发生情况（1981—2006年）、食心虫发病情况（1982—2006年）、黏虫发生情况（1979—2006年）。用于预测水稻产量的其他特征数据为水稻的竞争性作物种植面积与产量的历年数据，包括1949—2015年吉林省玉米、大豆种植面积、单产及总产量数据。

实验使用sklearn机器学习库进行数据的处理和SVR、MLP模型训练及预测。主要包括数据预处理、定义分类器、训练模型、模型预测等步骤。由于原始数据由多种特征数据组成，为高维数据，为了更有效处理数据，对原始数据进行主成分分析（PCA）降维处理后，再次进行上述分析流程，并与未经降维处理的预测结果进行对比。

采用每种方法建立预测模型时，考虑两种特征的组合：①考虑水稻生长受当年病虫害影响，采用病虫害数据预测当年水稻产量；②考虑竞争性作物种植面积及产量对农户种植意向的影响，采用竞争性作物种植面积及产量数据预测下一年水稻产量。两种特征组合可分别应用于当年及下一年水稻产量的预测任务。

（1）基于SVR的机器学习预测

对原始数据进行归一化处理后，将1950—1990年的数据作为训练集用于预测模型的建立，1991—2015年的数据作为测试集用于检验模型预测效果。

使用sklearn机器学习库SVR模型对水稻产量进行预测。主要步骤为：对原始数据中的缺失值进行函数填充后，对数据进行归一化处理；选择分类器为SVR，用训练集数据对模型进行训练，并建立预测模型；将测试集数据于模型预测效果的检验。对原始数据进行主成分分析PCA降维处理后，再次进行上述分析流程。

根据以上流程，利用病虫害数据预测当年水稻产量，得到预测曲线SVR1和SVR1（主成分分析降维）。利用竞争性作物种植面积及产量数据预测下一年水稻产量，得到预测曲线SVR2和SVR2（主成分分析降维）（图10）。

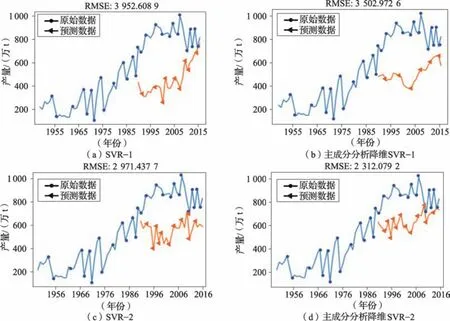
图10 利用支持向量机（SVR）模型预测水稻产量Fig.10 Prediction of rice yield using SVR model

SVR模型预测曲线呈波动上升，预测产量普遍低于实际产量，在一定程度上反应了原始数序列的波动情况。由分析结果可知，采用PCA对影响因素进行降维处理后，SVR模型预测准确性均有所提高。

（2）基于MLP神经网络的机器学习预测

使用sklearn机器学习库MLP模型对水稻产量进行预测。主要步骤为：对原始数据中的缺失值进行函数填充后，对数据进行归一化处理；选择分类器为MLR，用训练集数据对模型进行训练，并建立预测模型；将测试集数据于模型预测效果的检验。对原始数据进行主成分分析PCA降维处理后，再次进行上述分析流程。

根据以上流程，利用病虫害数据预测当年水稻产量，得到预测曲线MLP1和MLP1（主成分分析降维）。利用竞争性作物种植面积及产量数据预测下一年水稻产量，得到预测曲线MLP2和MLP2（主成分分析降维）（图11）。

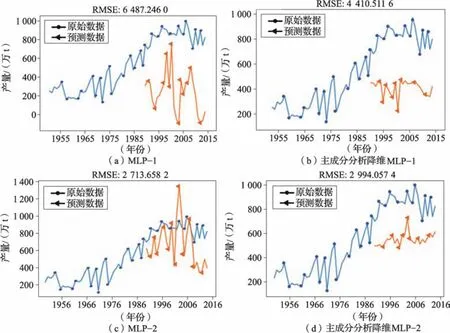
图11 利用多层感知器（MLP）模型预测水稻产量Fig.11 Prediction of rice yield using MLP model

MLP模型预测产量普遍低于实际产量，预测结果随原始数序列的波动出现剧烈波动。采用PCA对影响因素进行降维处理后，预测曲线波动性减缓，MLP1模型预测准确性提高，而MLP2模型预测准确性降低。

3 结果与讨论

利用吉林省病虫害和玉米大豆产量等历史数据，基于4种模型对吉林省水稻产量进行预测，预测值与实际值的RMSE见表1。基于ARIMA模型和LSTM模型的时间序列预测RMSE相对横截面预测RMSE较小，但预测值与实际值之间仍存在差距。在横截面数据预测中，原始数据经主成分分析PCA降维处理后，SVR1、SVR2和MLP1模型预测的RMSE值相对未经降维处理均有所下降，表明在数据维度过高、数据量较小情况下，降维处理在多数情况下可提升模型预测性能。

近年来我国对粮食生产实施了良种补贴、农机购置补贴、农民直补等一系列农业支持政策，加之生物技术、农业工程和管理技术的发展和农田水利基础设施的不断完善，使粮食持续增产潜力大大提升。利用ARIMA和LSTM进行时间序列预测时，只考虑产量随时间的变化趋势，没有考虑其他因素的变化对趋势延续性的影响，导致对近年产量的预测与实际情况相比偏低。

表1 不同方法预测结果RMSE值Table 1 RMSE of predicting results with different methods

农业生产是复杂的经济与自然再生产过程，粮食生产过程受到气象条件、作物品种、农资投入、田间管理、市场供需、国家政策等多方面的影响［18］。而利用SVR和MLP模型进行横截面数据预测时，模型训练使用的原始数据为水稻重要病虫害发生情况、大豆种植面积与产量、玉米种植面积与产量等数据，致使模型主要反映水稻产量与病虫害发生情况及竞争性作物种植情况的关系，没有考虑其他影响产量的气象因素、投入管理因素、社会经济因素，导致模型预测产量与实际产量相比偏低。

由时间序列模型与横截面数据预测模型对比的实证分析结果可知，在进行水稻产量预测时，如缺乏影响产量的重要因素的数据，则应用时间序列模型分析结果较好。反之，如掌握影响产量的重要因素数据，则宜采用横截面数据预测模型。在进行横截面数据预测时，如分析影响因素较多，可采用PCA对影响因素进行降维处理，通常能够提高预测结果的准确性。此外，在进行横截面数据预测中，如训练数据较少时，采用回归模型比神经网络模型预测结果准确性高，且神经网络模型中，在训练数据量较小时，算法表现不够稳定。在进行横截面数据进行水稻产量预测时，利用竞争性作物种植面积及产量数据预测下一年水稻产量的结果优于利用病虫害数据预测当年水稻产量。

在后续研究中，拟通过补充气象数据、农资投入等数据，提高基于SVR和MLP模型的横截面数据预测准确性，并通过构建时间序列预测和横截面预测组合模型，进一步提高水稻产量预测的精度。