从碎片化解题走向结构化解题
——基于核心素养的“自然而然法”解题模式简介
徐祥宝
(苏州市教育科学研究院,江苏 苏州 215004)
1 引言
习题课是物理课堂教学的重要课型,也是中学物理教学必不可少的一个重要环节.物理解题的功能在于让学生在解决问题的过程中加强概念辨析、进一步深刻理解概念,让学生在解决问题的过程中理解规律、掌握规律,让学生在解决问题的过程中运用知识、进行迁移拓展提升能力,从而实现物理思维方法的教育功能和培育物理学科核心素养[1].
所以,解题是学习物理的必由之路.由于物理习题中的情景紧密联系生活、科技,且在物理习题中各物理量之间的时间、因果、空间等等关系都尽情展现,物理事件环环相扣,整个物理问题就是一个有机整体,其复杂性使解题教学成为抓住物理核心素养教育的非常重要的任务,利用物理解题实施物理核心素养教育是行之有效的[2].因此,只要教师从解题入手,培养学生的反思意识,必将有利于学生物理素质的提高,真正体现物理解题的教育功能.
2 解题教学之困惑
在具体实施解题教学时,师生通常会有诸多困惑.
(1) 教师之困惑.
在具体进行解题教学时,许多教师认识到:审题是解对题的前提,对物理题的审题主要是明确题中告知的已知条件、隐含条件以及求什么.在具体进行解题教学时,许多教师也都明白:要让学生既听懂、又学会,就必须对学生进行思维训练.因此,许多教师采用:一题多解,提高学生思维的深度;一题多变,提高学生思维的广度;一题多测,提高学生发散思维能力;多题归一,提高学生聚合思维的能力[3];以此来培养学生的思维能力,提升学生的核心素养.
更有甚者,有的教师为了提高学生的解题能力,甚至总结了解决物理实际应用题目的一般程序.
① 审题.提取题目中与物理模型有关的信息,如:物理现象、物理事实、物理情景、物理状态、物理过程等.
② 提取题目中的主要因素,寻找关键词.
③ 搜索与已有知识(如:实体、系统、过程等)相近的或直接的联系,通过类比分析、联想概括、逻辑推理或原型启发等,建立物理模型,将新情景问题转化为常规问题.
④ 选择与物理模型相关的物理规律求解[4].
然而,实际情况是:有些试题教师讲了许多遍,学生自己也做了许多遍,甚至考试还考了许多遍,但结果是题目稍有变化学生仍然是错了许多遍.所以,教师困惑:为什么学生会“一听就懂、一点就通、一变就蒙、一做就错”;为什么教师讲得越明白学生会感到越糊涂呢?
(2) 学生之困惑.
解题教学后,听到学生最多的声音是“上课时我能听懂老师讲的内容,可是到自己做的时候就不会了”,“对于相对复杂的问题,我们普遍会处于无目标状态,不知道自己下一步要做什么,也不知道该从什么地方下手去做,更不知道怎样才能得出符合要求的结果,解题效率很低,更不用说提升物理核心素养了”.
所以,学生困惑:为什么教师想到的解题方法我就想不到呢?物理真的这样难学吗?
3 原因分析与解决方法
(1) 原因之分析.
在具体解题时,已知条件和求什么学生一般较易找到.但隐含条件如何寻找?哪些属于关键词?解题的切入点在哪里?待求量和已知量之间到底存在怎样的关系?对于这些问题,学生是非常茫然的.平时解较复杂的题目,这些关键点都是在老师的点拨下获得的,学生可能不是真正弄懂的,所以学生会感到有些试题老师讲了很多遍,自己做了很多遍,考试考了很多遍,结果题目稍有变化还是错了很多遍[5].
最主要的原因是碎片化解题.
由于学生的课堂学习时间是有限的,且教材是按照教学内容进行排列的,因此相同的方法往往是在知识学习的同一阶段使用的,不同的知识学习阶段使用不同的方法,无疑方法的使用是碎片化的.上面教师所讲的解题一般程序仍然是碎片化的,没有形成范式和套路,可操作性不强,学生依旧不知道如何审题、怎样寻找隐含条件、如何确定关键词,解题思路迷茫,解题方向不明确.如果平时解题教学仅仅是碎片的堆砌,就缺少前后联系思考和抽象的想象,这样的过程难以让学生形成对方法的认识,难以掌握真谛,更难获取通用的高层次规律.所以,只有让学生掌握了解决一类问题的一般方法,学生才能在正确的解题思维指导下,科学、合理地解决问题,学生才能真正学会如何去思考,学会用什么方法去解决,学会如何找到突破口,让解决物理问题变得更轻松,学习更有趣,效率更高.所以我们必须把主动权交给学生,使学生获得分析问题、解决问题的钥匙,大大提高解决问题的能力,提升核心素养.
(2) 解决之方法.
最好的解决方法是结构化解题,让学生掌握解决一类问题的一般方法.
结构化方法解题,就是培养学生建立科学解题思想,让学生用学到的学科知识利用科学的方法解决问题,结构化方法解题是基于结构化思维的一种解题方法.
所谓结构化思维,就是在思考分析解决问题时,以一定的流程顺序进行的一种范式和套路.掌握结构化思维,就能熟练使用某种方法有效地解决某一类问题.
4 结构化解题模式简介
结构化解题模式能让学生自然而然的确定解题切入点,在确定切入点的基础上自然而然地寻找一系列的问题链——将一道习题变成一个问题链,将一个复杂的问题转化为一个个简单但具有相互关联的小问题.让学生在解决一个个小问题的过程中自然而然的去审题、去分析过程、去找相关的关键词、去分析相关图像、去建模,从而能自然而然的寻找到隐含条件,顺利解决问题.所以,我们将结构化解题模式也称作“自然而然法”解题模式,此模式具有很强的可操作性.
“自然而然法”解题模式主要凸显三个方面.
4.1 具体应用分析法的思路
物理习题纷繁复杂,不要幻想一下子解决整个问题.如果能把大问题(较复杂的问题)分解成若干个小问题(较为简单的子问题),逐个将小问题(子问题)解决,最终就可完整的解决大问题(较复杂问题).笛卡尔也曾说过:“把你所考虑的每一个问题,按照可能和需要分成若干个部分使它们更易于求解.”对分解出来的子问题进行解答,然后再经过叠加或组合就可得到原问题的答案[5].
这就是化整为零各个击破的策略,它是攻克复杂问题的一大法宝.如何在已知与未知之间建立桥梁?可有两个方向,也就是说解决问题有两种思路,即综合法和分析法.所谓综合法,就是从条件到结论的思维方式.从给定的条件出发,朝着结论的方向一步步推导,然后顺利到达终点,这就是综合法.如果是从结论到条件的思维方式,则就称之为分析法.我们首先盯住结论,问想要得到这个结论需要知道什么条件?为了得到这个条件又需要知道哪个条件,为了那个条件又需要证明什么?这样一步步推导,顺利到达已知的条件,整个问题解决就结束了.比较而言,分析法更容易让人把握住思路,就中学生的认知特点和能力而言,分析法的思路是值得推荐的,它往往可以直达问题的本质.
分析法如何应用于物理解题?
首先,我们要解决什么问题,那么,理所当然这个问题就该是解决的切入之处,所以所求量就是切入点.其次,隐含条件是什么? 我们首先盯住这个所求量,思考想要得到这个所求量需要知道什么条件?为了得到这个条件又需要知道另外的什么条件?依次推导,可顺利到达已知的条件,整个问题解决就结束了[1].其中构建所求(未知)量和已知条件之间的桥梁,就是它们中间的过渡条件,也就是所谓的隐含条件.所以,隐含条件就是求解未知量的物理规律(公式)或结论等.思维程序如图1所示.
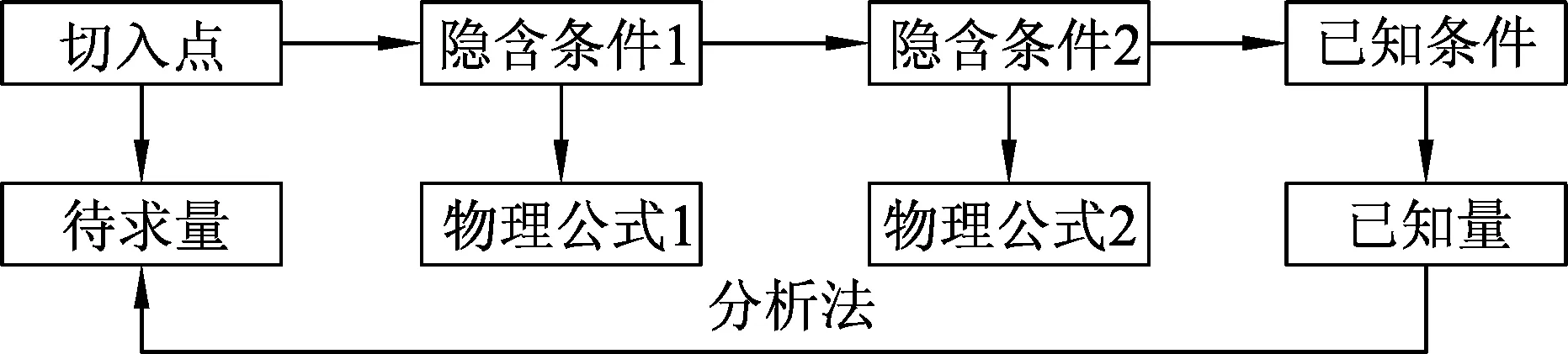
图1
案例1.(为了简洁的说明问题,选取初中习题作为案例).
小明家使用的是天然气热水器,其最大容积为40 L.装满15 ℃的水后进行加热,当水的温度达到40 ℃时,小明家的天然气表的示数从2365.89 m3变为2366.05 m3.已知天燃器的热值为3.2×107J/m3,求该热水器的热效率.


(2) 解答过程(倒过来写).
水的质量为m=ρ水V水=1×103kg/m3×40×10-3m3=40 kg,
水吸收的热量为Q有用=Q水吸=cm(t-t0)=4.2×103J/(kg·℃)×40 kg×(40 ℃-15 ℃)=4.2×106J;
燃气的体积为V燃气=V2-V1=2366.05 m3-2365.89 m3=0.16 m3;
燃气燃烧放出的总热量为Q总=qV燃气=3.2×107J/m3×0.16 m3=5.12×106J;
分析法突出了解题思路的结构性与逻辑性.
4.2 呈现思维可视化的过程
“自然而然法”解题模式引入思维导图,思维导图作为一种思维可视化的工具,可将问题解决的思路和过程呈现出来,不仅有利于学生学会如何分析、思考、解决问题,而且有利于学生进行反思.上题解题时边分析边记录的思维导图如图2所示.
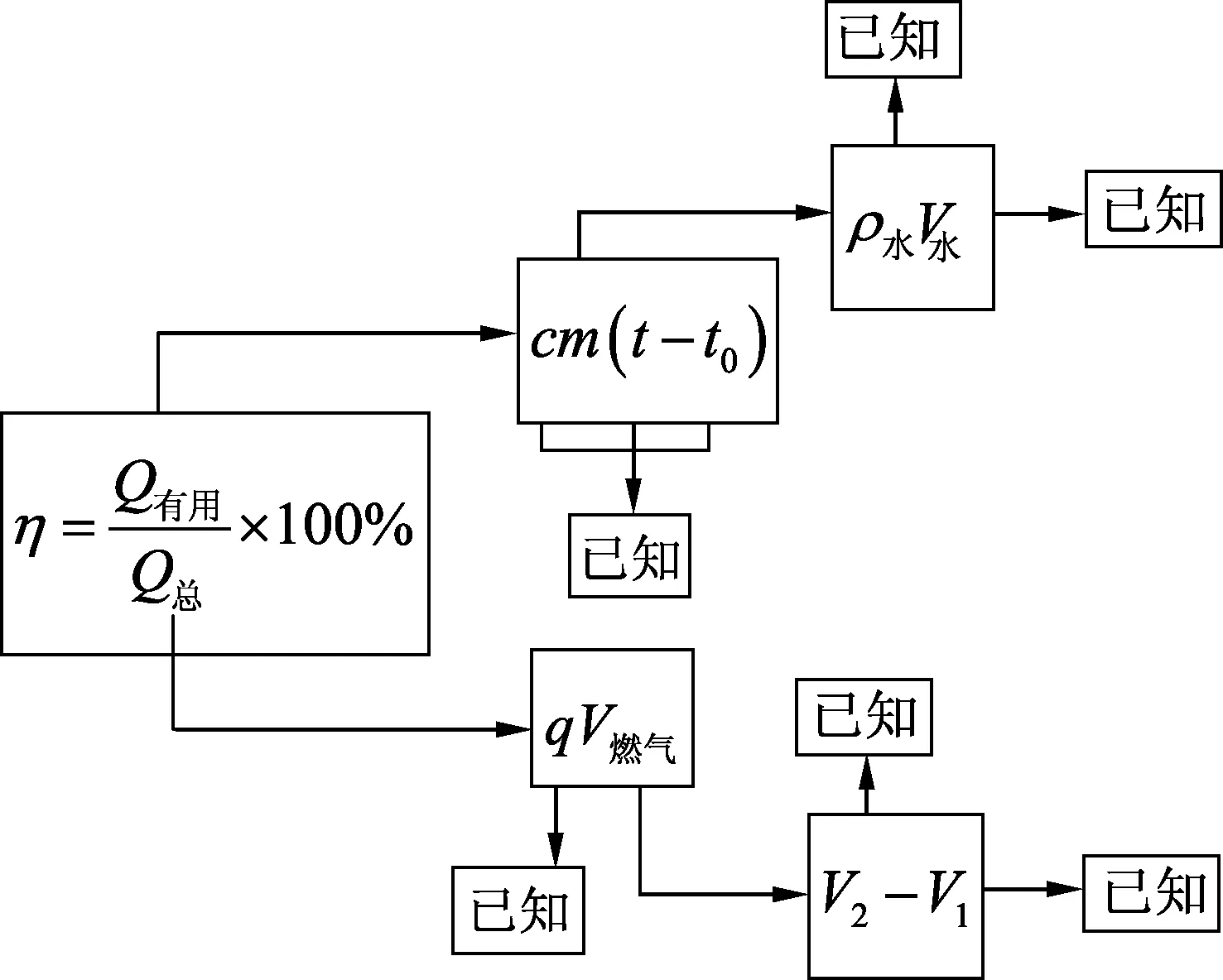
图2
利用思维导图解题,能够结构化呈现分析过程,可以清晰地看到解题的内在思路,过程分析清晰全面,解题思路一目了然.运用思维导图完成解题,可形成好的解题流程、使解题过程模式化,对学生解决物理问题有很大的帮助.利用思维导图解题不会出现思维断裂,有利于发现解题中的问题,便于思考解决对策,易于及时调整,是克服解题思维中思维障碍的有效方法.
4.3 试错逼近多角度的指向
采用结构化思维方式,对所研究的问题进行多侧面、多角度的“试错逼近”目标,从而探索出解决问题的最佳途径,提高解题技巧,同时也可培养学生处理实际问题的本领,提升核心素养.
案例2.(2016年青岛市中考题)小雨通过如图3(a)所示滑轮组将水中物体匀速提升至空中,他所用拉力F与绳子自由端移动的距离s的关系图像如图3(b)所示.物体在空中匀速上升过程中滑轮组的机械效率为85%,每个滑轮等重,不计绳重、摩擦和水的阻力.求物体的密度是多少?
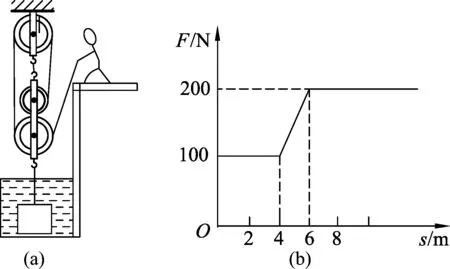
图3
在解题时,边分析边记录的思维过程导图如图4所示.
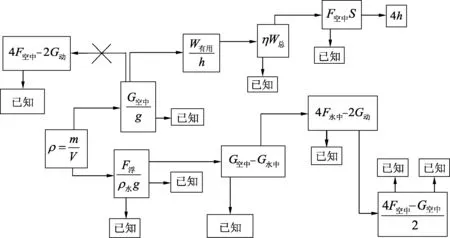
图4
(2) 解答过程(略).
综上所述,我们可将“自然而然法”解题模式用下列简化图式图5表示.

图5
4.4 运用模式解决复杂问题
案例3.给你一个额定电压为3.8V的小灯泡,一个电压约为9V的电源,滑动变阻器一个,定值电阻R0一个,开关3个,导线若干,要求只用一个电压表测量小灯泡的额定功率,测量时不得改变电路的连接,请设计出测量电路图.
利用“自然而然法”解题模式,可将该比较复杂的设计问题分解成一连串简单的有关联的问题:如常规的功率测量→特殊测量(单表测量)→特定要求测量.
(1) 常规的功率测量设计.
设计思路导图:
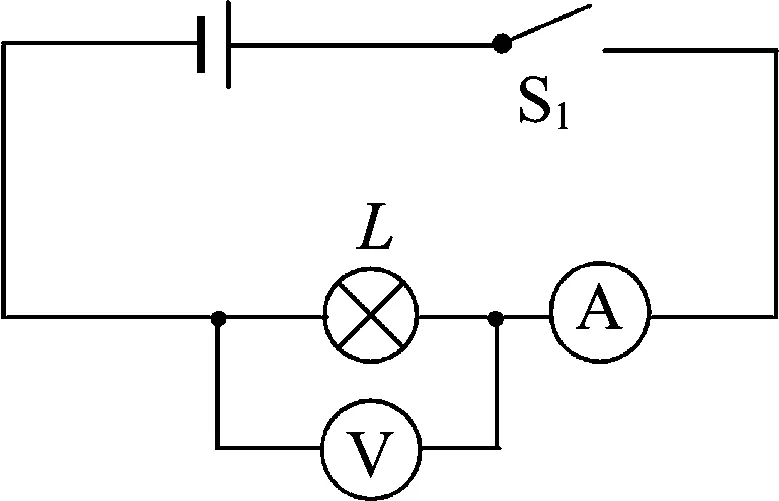
图6 图7
分析题意发现,题目要求测额定功率,故所测电压必须是额定电压,现电路所测电压不保证是额定电压,则必须通过滑动变阻器进行调节,使加在灯泡两端的电压为额定电压,可设计出如图7所示电路图.
(2) 特殊(单表)测量设计.
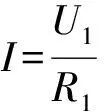
设计思路导图(如图8):
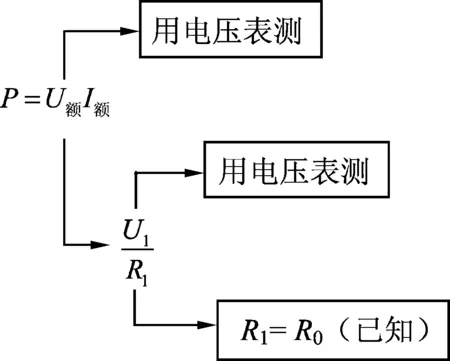
图8
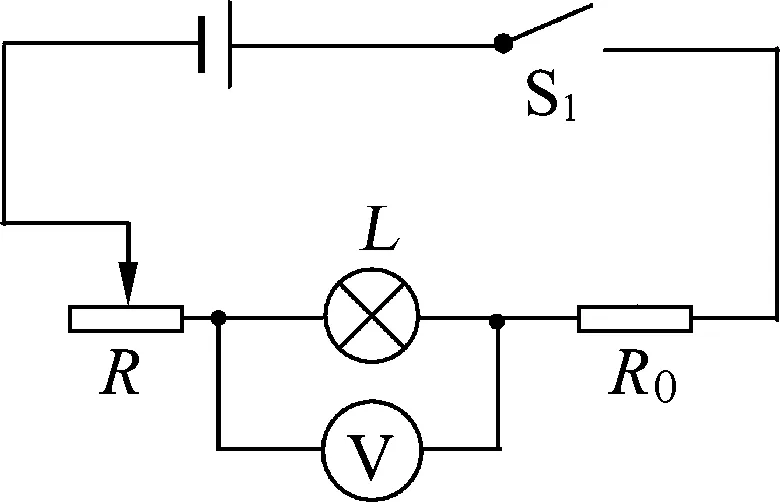
图9
因为是用定值电阻R0替代电流表,所以R0应接在原电流表的位置,R0也只有与灯泡串联,才能保证通过它的电流也就是小灯泡通过的电流,由此可得如图9所示电路.
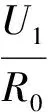
(3) 特定要求测量设计.
分析题意发现,题目要求测量时不得改变电路的连接,故电压表不能用来直接测量U1,但其可由串联电路特点求得,U1等于灯与定值电阻两端的电压U2减去U额设计思路导图(如图10):
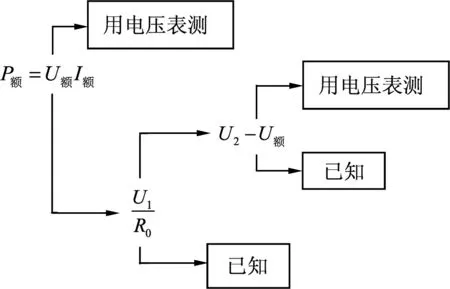
图10
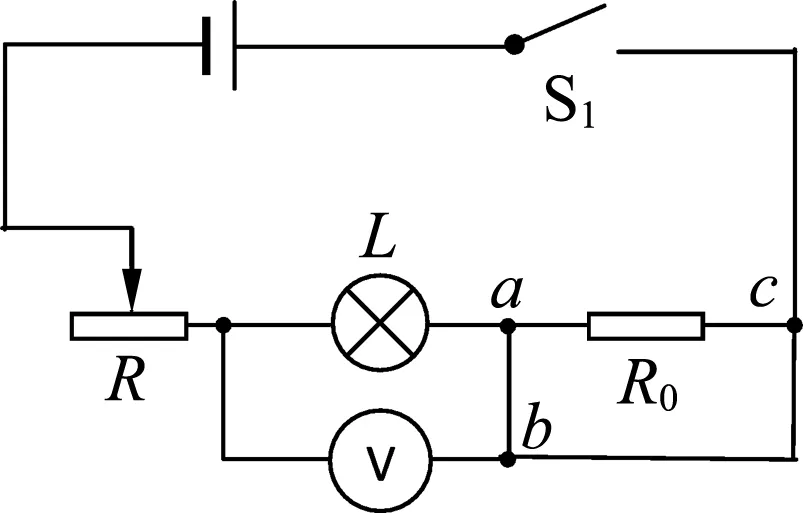
图11
关键是要测出U2,但电压表又不好移动,所以必须将b与c两点用导线连接起来才有可能测量,如图11所示.但此时电压表测出的电压并非是U2,因为R0被短接了,只有断开ab导线,电压表才能测出U2,所以ab导线在测U额时要连通,在测U2时要断开,要达到该要求只能在ab导线中串接一个开关S2,如图12所示;同理,在测U额时bc导线要断开,在测U2时要连通,要达到该要求也只能是在bc导线中串接一个开关S3,如图13所示.
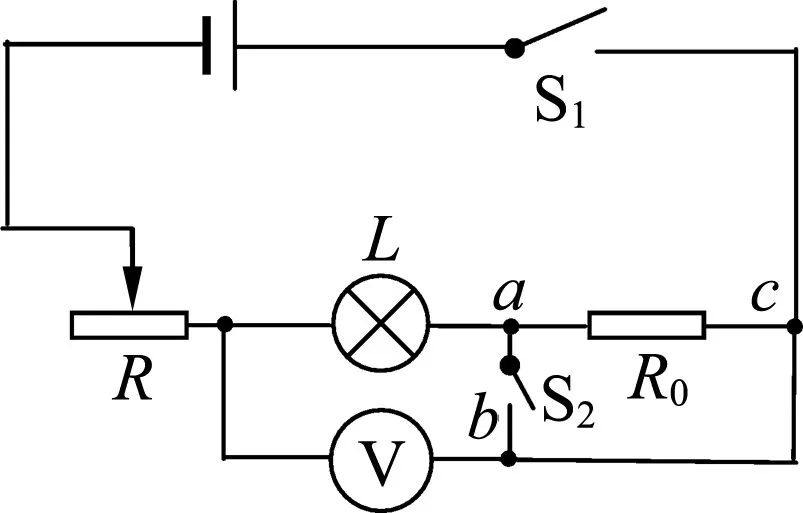
图12
至此测量电路图设计完毕,问题基本完整解决.
具体操作为:滑动变阻器阻值放在最大值;闭合开关S1和S2,断开开关S3,调节滑动变阻器使得电压表的示数为U额并记录;断开S2,闭合S3,测得电压U2并记录.
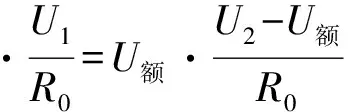
5 结语
综上所述,“自然而然法”解题模式具有如下优势.
(1) 可单刀直入找准切入点,不需化时分析;
(2) 能够把握解题思路且指向明确;
(3) 通过化整为零各个击破的策略,可将大(复杂)问题拆成小(简单)问题,逐个将小(简单)问题解决,大(复杂)问题最终就可完整解决.
(4) 可在解决一个个小问题的过程中,自然而然的有目的的且具有针对性的进行审题分析、寻找隐含条件、确定关键词、进行建模和用好已知条件,在试错逼近过程中寻找最优解题途径;
(5) 由于“自然而然法”解题模式应用了思维导图,使思维过程可视化了,在分析问题过程中可防止思维断裂,使解题方向更确定.
总之,“自然而然法”解题模式适合于任何题型和各年级段,是一种普适的可操作性强的解题范式和套路,能够有效培养学生思维的严密性、逻辑的严谨性、科学辩证的分析问题的能力,特别能提升学生解决新问题的关键能力,培育物理学科核心素养.

