基于INS/GNSS紧耦合组合的逐步诱导式欺骗检测算法研究

武智佳，吴文启，刘 科，唐康华

(国防科技大学智能科学学院，长沙 410073)

0 引言

在近年来的几次局部战争中，依靠卫星导航的设备与制导武器在战场中扮演了极为重要的角色[1]，但是也暴露了全球卫星导航系统(Global Navigation Satellite System，GNSS)信号弱，极易受到干扰和欺骗等缺点，很容易实现让GNSS接收机优先地捕捉到欺骗信号，并且具有较强的隐蔽性[2-3]。欺骗式干扰主要分为生成式和转发式，相比于生成式，转发式不仅针对民码信号，对军码信号也可以通过干扰器进行延时放大并转发，进而影响接收机获取的伪距信息[4]。但当导航和制导设备采用惯性导航系统(Inertial Navigation System，INS)/GNSS组合导航方式时，利用INS的短期稳定性，这种延时转发的方式容易引起定位跳变被INS识别，进而停止GNSS对INS的校正。为此，文献[5]研究了轨迹诱导式欺骗方法，通过雷达等监测方法，探知载体的位置和速度信息，然后利用转发式干扰器，实施相应的位置欺骗和速度欺骗策略，使目标载体获得错误位置及速度，在不易被INS识别的情况下逐步诱导载体控制器拉偏运行轨迹。而现阶段从惯性信息辅助方面提出的抗欺骗方法，主要都是利用单方面的惯性信息，如加速度计辅助对比[6]、位置辅助接收机自体完好性监控(Receiver Autonomous Integrity Monitoring，RAIM)检测[7]、位置跟踪数学评估[8]、基于载波相位双差的姿态辅助[9-10]、通过多普勒测速的速度辅助[11]等，对这种逐步诱导的欺骗方式，单一状态的惯性信息辅助检测效果会出现不明显的情况。

为此本文提出了一种基于INS/GNSS紧耦合组合的逐步诱导式欺骗检测算法，从速度和位置两种惯性信息出发，研究了位置欺骗和速度欺骗对伪距测量和伪距率测量带来的影响，并结合INS短时间位置误差传播模型，分析了真实信号和欺骗信号下伪距和伪距率变化的一致性关系，并构造了时间序列模型来实现信号的判别，并对不同的判别结果做出不同响应。最后根据逐步诱导式欺骗原理，设计了仿真实验验证本算法的有效性。

1 逐步诱导式信号欺骗原理

逐步诱导式欺骗[5]的基本原理即通过雷达等监测方法去探测目标载体的位置和速度信息，设计欺骗策略使GNSS接收机捕获欺骗信号，解算出错误的位置和速度，以小的定位偏移逐步诱导载体偏离预定轨迹。

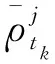
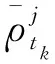
(1)

式中,Δρj为欺骗伪距在真实伪距基础上的附加伪距，而速度欺骗是根据欺骗策略中设定的欺骗速度，通过调整速度解算所需要的多普勒频率来达到欺骗目的。而伪距率的通常计算方法为

(2)

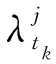
(3)

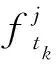
2 INS辅助的欺骗检测方案

图1所示为本研究欺骗检测流程的示意图，先在短时间内进行惯性导航，获取INS数据和GNSS数据。经过检测算法判定，对于真实信号，利用这些数据重新进行伪距、伪距率紧耦合组合，以修正原惯性导航轨迹和INS输出，然后进入下一短周期继续该流程，若为欺骗信号，则继续用惯性导航，并采取相应措施。

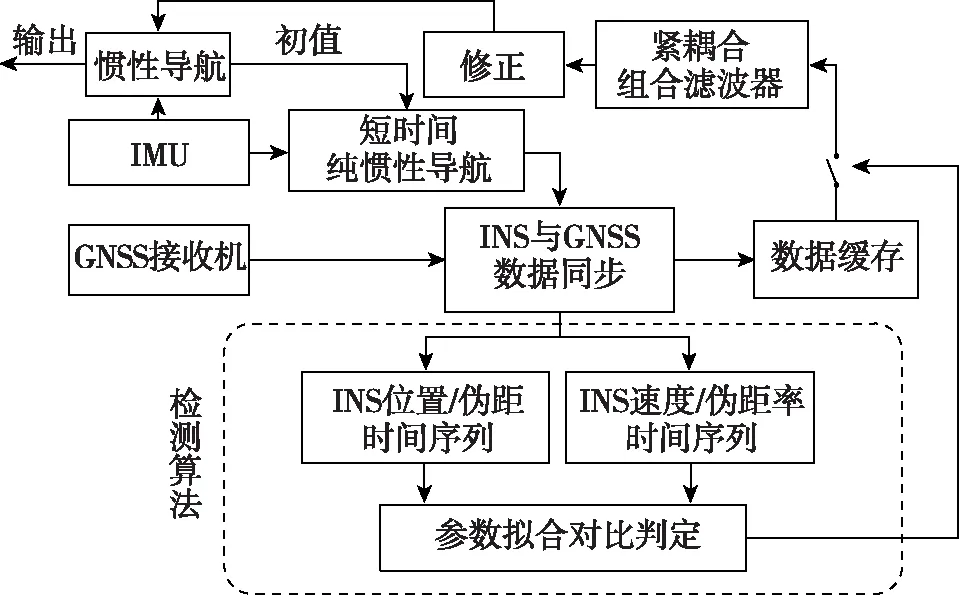
图1 欺骗检测流程示意图Fig.1 Schematic diagram of deception detection process

2.1 短时间欺骗检测模型

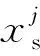
(4)

因载体的运动可以在ECEF坐标系内分解为3个坐标轴的运动，所以根据文献[13]可知，对于INS在无校正状态下，每个分运动在短时间内的位置误差随时间的变化关系可近似为二次函数。由此分析可知，接收机在短时间内的真实位置可由INS输出的位置经误差修正后估计得到，若从t0时刻开始对真实位置的坐标进行估计，则在tk=t0+tm时刻真实位置对应的ECEF估计坐标为

(5)

(6)

式中：

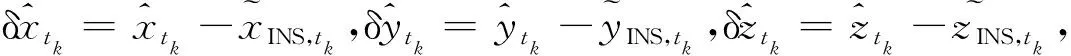
(7)

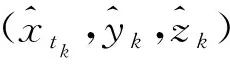
(8)

整理式(8)可得

ey,t0κy1+ez,t0κz1)tm+(ex,t0Δx+ey,t0Δy+

(9)

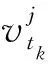
(10)

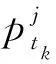
(11)

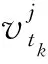
≈2(ex,t0κx2+ey,t0κy2+ez,t0κz2)tm+

(ex,t0κx1+ey,t0κy1+ez,t0κz1)

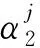
(12)

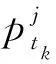
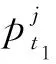
(13)

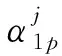
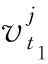
(14)

(15)

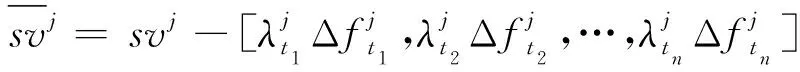
(16)

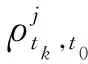
综上分析，通过对比2个时间序列模型的拟合参数和观察2个时间序列模型的拟合程度即可实现对欺骗信号的检测。

2.2 INS/GNSS紧耦合组合系统状态方程

本文采用伪距、伪距率紧耦合组合导航方案，将导航坐标系选为北东地，其紧耦合组合系统状态方程包含INS和GNSS两部分，可写为

=F(t)X(t)+W(t)G(t)

(17)

其中，F(t)为系统状态矩阵，W(t)为过程噪声矩阵，G(t)为系统噪声矩阵，17阶状态向量X(t)为

X(t)= (φE,φN,φU,δvE,δvN,δvU,δL,δλ,δh,

(18)

2.3 INS/GNSS紧耦合组合系统量测方程

(1)伪距量测方程

已知惯性导航的位置为(xINS,yINS,zINS)，则其所对应的卫星信号j的计算伪距为

(19)

结合接收机测量改正后的伪距ρG，得到伪距的量测方程

Zρ(t)=ρINS-ρG=Hρ(t)X(t)+Vρ(t)

(20)

其中，Vρ(t)为伪距测量噪声。根据状态向量的定义，需要把大地坐标误差 (δL,δλ,δh)变化为ECEF坐标误差 (δx,δy,δz)，变换矩阵为

(21)

则观测矩阵

(22)

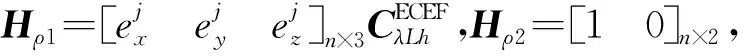
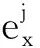
(2)伪距率量测方程

(23)

(24)

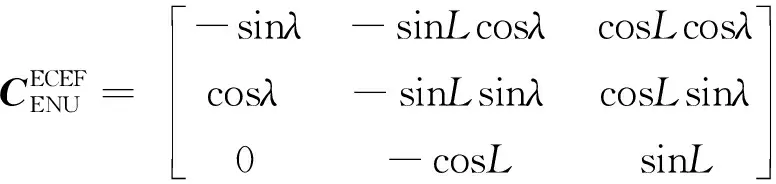
(25)

则观测矩阵

(26)

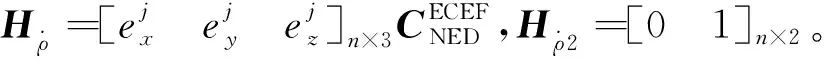
将式(20)和式(24)合并,得到伪距、伪距率紧耦合组合系统的量测方程

(27)

3 仿真验证

为了验证算法的可行性和有效性，本文利用无人机飞行数据，根据逐步诱导式欺骗原理设计欺骗方案，其仿真条件为：

1)可见卫星7颗，仿真时长10min。GNSS数据采样频率2Hz，惯性传感器信号输出频率200Hz。短时间周期设定为5s。初始经纬度分别为50.9887°和12.5176°，高程为229.2790m。

2)姿态角初始对准精度0.5°，陀螺随机漂移10(°)/h，加表零偏为0.3mg，伪距测量精度25m，伪距率测量精度0.5m/s。

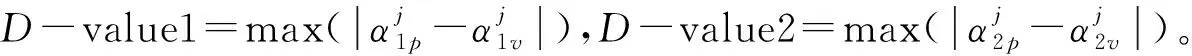
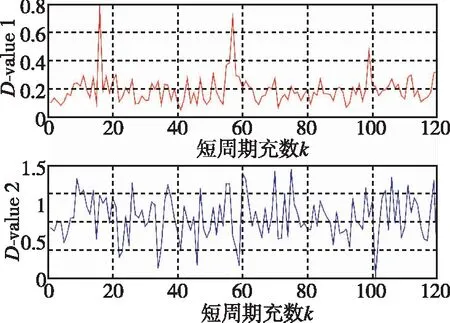
图2 真实信号时各短周期拟合参数差值Fig.2 Short period fitting parameter differences of real signal

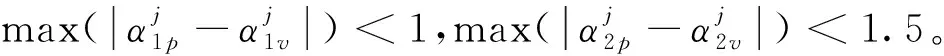
为了验证算法的有效性，设计仿真在450s时，根据雷达定位和测速性能[15]设计表 1的ΔP和ΔV，并结合文献[5]设计欺骗信号，对卫星坐标进行Sagnac改正。由式(10)和式(12)可知，其INS位置相对于卫星的余弦向量也影响着拟合参数的大小，仿真观察余弦向量与误差模型参数组合后数值较大的5号星为参考，并观察第一个被欺骗短周期的参数值关系以及相关数值变化趋势。表中位置偏移ΔP=[Δpx,Δpy,Δpz]，速度偏移ΔV=[Δvn,Δve,Δvd]。

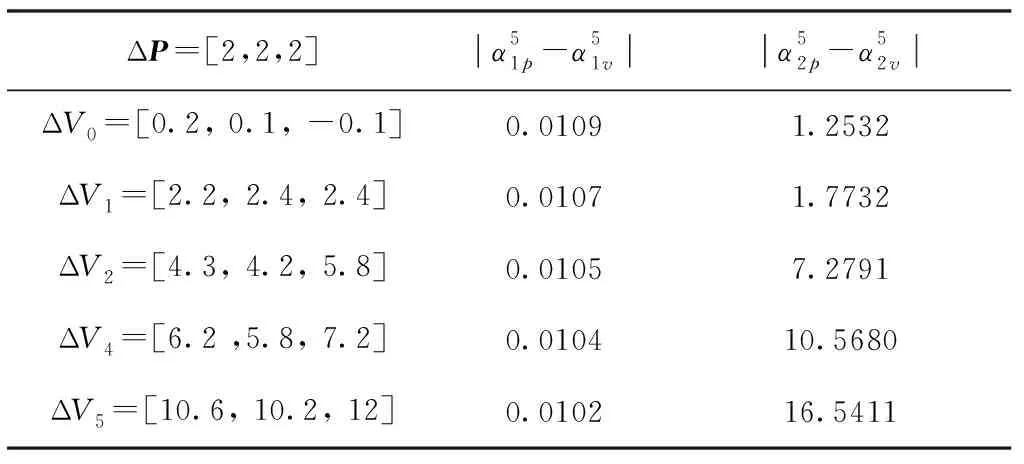
表1 欺骗检测效果分析Tab.1 Analysis of the deception detection results

在无位置和速度欺骗时，表中2个数值分别为0.0282和0.6237。

在图3和图4中，ΔV0代表无欺骗时的时间序列，标签中数字代表拟合优度系数R-square，用于评价曲线的拟合程度。由表1可以看出，在小的定位偏移下，速度偏移在2m/s以上时，表中差值产生显著变化，且随着偏移量的增加逐渐增大，据此可以检测出欺骗信号的存在。从图3和图4中可以看出，在无欺骗信号存在时，时间序列sp5和sv5基本可以按二次函数和一次函数做拟合，且拟合结果之差趋向于0，证明了真实信号的2个序列模型参数具有一致性。而存在欺骗信号后，速度偏移在2m/s以上时，随着偏移量的增加，各时刻的数据逐渐变大，并且在短周期内数据趋势满足函数模型的效果变差，即2个模型参数不一致性变大，由此可知，该算法对这种诱导式欺骗较为敏感。

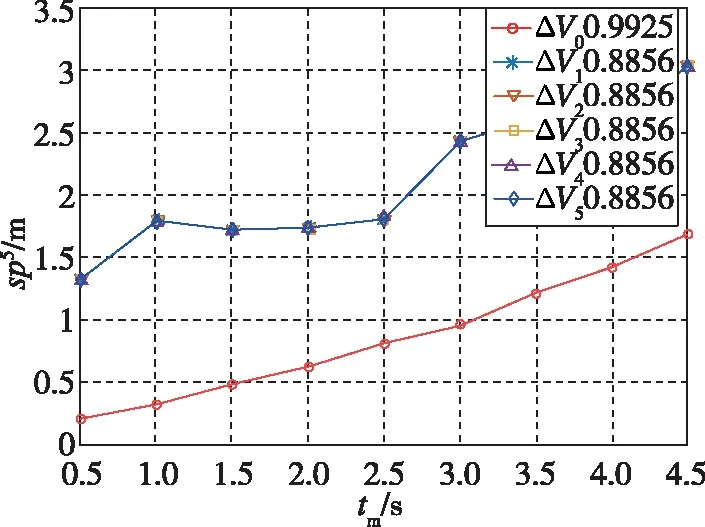
图3 位置/伪距时间序列sp5趋势Fig.3 Trend of the position/pseudo-range time series sp5

图4 速度/伪距率时间序列sv5趋势Fig.4 Trend of the velocity/pseudo-range rate time series sv5

4 结论

本算法是针对逐步诱导式欺骗，在短时间内进行纯惯性导航，从位置和速度两种惯性信息出发，并基于在真实信号和欺骗信号下，伪距和伪距率随时间变化的一致性关系提出了一种欺骗检测方法，主要结论如下：

1)该方法既能检测到单一的位置欺骗或速度欺骗，又能快速地检测到对小定位偏移下的诱导欺骗，便于载体控制者及时地采取措施，弥补了传统方法单一状态辅助检测可能出现大概率漏检的缺陷。

2)存在速度和位置偏移时，其时间序列模型的拟合程度变差，据此也可以反映出欺骗信号的存在。且算法基于INS短时间的误差传播关系，因此，对惯导设备要求不高。

3)本算法是从伪距方程和伪距率方程出发进行探究，其接收机伪距、伪距率测量精度越高，检测效果越好。

综上，本文提出的方法和结论为这种较为隐蔽的逐步诱导式欺骗检测提供了参考方案，在无人机对抗等导航领域有着较强的应用价值。