基于模拟退火算法的锂电池模型参数辨识*

罗 勇，祁朋伟，阚英哲，李沛然，刘 莉，崔环宇

（1.中国汽车工程研究院股份有限公司，汽车噪声振动和安全技术国家重点实验室，重庆 400054；2.重庆理工大学，汽车零部件先进制造技术教育部重点实验室，重庆 400054；3.重庆青山工业有限责任公司技术中心，重庆 400054）

前言

电池管理系统（battery management system，BMS）的开发是新能源汽车关键技术之一，电池荷电状态（state of charge，SOC）估算是BMS最基础和核心的功能［1］。由于电池具有非线性特性，准确估算其SOC一直是BMS开发的重点和难点。对电池充放电特性进行研究，在理论分析与特性试验基础上建立精确的动力电池模型，不仅能对电池的特性和行为过程进行仿真，且是准确估算电池SOC的关键［2］。

动力电池建模常采用等效电路模型，常用的等效电路模型有Rint模型，RC网络模型，Thevenin模型和PNGV模型等［3-4］。其中RC网络模型能准确反映电池特性和工作原理，其阶数越高，拟合效果越好，但也增加了建模的复杂度，降低了模型求解的实时性［5］。2阶RC网络模型采用两个RC网络结构描述电池的电化学极化和浓差极化现象，能很好地反映电池的动静特性［6］，且RC阶数不高，模型求解实时性好、参数辨识较易实现，在实际中应用较多。

动力电池在充放电过程中内部的电化学反应非常复杂，且具有时变性和非线性特性，其RC参数会随着充放电倍率，SOC和温度的不同而发生较大改变［7-8］。要建立准确的电池模型，则须在不同充放电倍率和SOC等条件下对RC参数进行辨识。电池管理系统实际工作过程中通过实时采集电池状态参数来估算SOC［9-10］，对电池状态参数时变性和准确性提出了较高要求，尤其须对不同状态下的RC参数进行辨识。

目前常用的电池模型参数辨识方法有最小二乘拟合法、卡尔曼滤波法和遗传算法等。最小二乘拟合法计算简单，工作量小，但误差较大［11］。卡尔曼滤波法能得到状态变量的最优估计，但须预先知道状态变量的初始值，且严重依赖噪声的统计特性［12］。遗传算法对全局有较好的辨识精度，但局部搜索能力较差，对初始种群有一定的依赖性。

模拟退火算法是一种新的随机搜索方法，具有无需初始参数、收敛速度快的特点。模拟退火算法具有渐进收敛性，已被证明是一种能保证获得全局最优解的全局优化算法［13］。基于动力电池充放电“回弹曲线”进行参数辨识需要大量数据［14］，采用其它算法存在参数辨识过程中参数初始值未知和易陷入局部最优点的问题。而采用无需初始参数、收敛速度快、能获得全局最优解的模拟退火算法对电池RC参数进行辨识，不仅能解决动力电池模型参数初始值未知的问题，还可提高参数辨识效率。

本文中以锂电池为研究对象，建立其2阶RC理论模型，通过试验获取电池在不同充放电电流和SOC下的充放电特性数据，在此基础上通过模拟退火算法辨识得到不同放电倍率和SOC下理论模型的RC参数，并将其制成随放电倍率和SOC变化的数表。电池管理系统在线运行时，可通过查表实时获取电池模型参数［15］。在 MATLAB／Simulink中搭建动力电池模型，采用模拟退火算法对动力电池参数辨识的准确性进行仿真和试验验证。可在不同温度条件下重复本文的辨识工作，从而获得更为全面的RC参数在不同温度下随电流和SOC的变化特性，本文的算法研究为相关工作奠定了基础。

1 动力电池理论建模与参数辨识原理

1.1 电池2阶RC模型

当电池处于充放电等动态工况时，其内部会产生电化学极化和浓差极化，端电压发生动态变化。研究显示，2阶RC网络模型能很好地模拟电池内部的化学特性，对其动态工况下电压变化进行描述，等效电路模型如图1所示。其中，Ub表示电池的开路电压；R0表示电池欧姆内阻；两个RC结构表示电池的极化反应；R1和R2表示电池的极化内阻；C1和C2表示电池的极化电容；I表示流经欧姆内阻R0的电流；U表示电池两端可直接测得的端电压。

图1 2阶RC等效电路模型

根据图1可得2阶RC等效电路模型的状态方程和输出方程：

式中：U1′为极化电容C1两端电压U1的1阶导数；′为极化电容C2两端电压U2的1阶导数；［U1为状态变量。

1.2 动力电池回弹特性分析与RC参数辨识原理

对某一具体的电池系统，上述模型中的RC参数须通过以测试数据为基础的参数辨识获得。选取一种能集中反映电池动态特性的典型工况进行理论分析与试验测试，是对电池进行参数辨识的首要工作。

电池电压回弹特性是指当电池充放电回路断开后，电池端电压并不是立刻静止在某一值，而是会经过一段时间的波动后逐渐趋于稳定的现象。这种现象是由于电池内部受到电池的电化学机理的影响，电极的净反应速率不会立刻为零。研究显示，电池的电压回弹特性较为集中地体现了其动态特征，可作为对电池进行参数辨识的典型工况［14］。

电压回弹特性与2阶RC模型吻合，可用2阶RC模型加以解释，这也是通常用电压回弹特性进行2阶RC模型参数辨识的基础。以放电过程为例分析电池电压回弹特性，电池在放电结束后静置，其端电压变化过程如图2所示。采样时间间隔为1s，图中A点表示放电结束时刻，B点表示放电结束后的第1个采样时刻，C点表示电压趋于稳定的时刻。可以看出，静置过程中电池端电压变化可分为迅速上升阶段AB和缓慢上升阶段BC。放电结束后，AB阶段电压快速回升主要是受到欧姆内阻的影响，为断电瞬间欧姆电阻的电压响应；BC段上升缓慢是受到电池极化的影响，可等效为2阶RC的电压响应。可见，电压回弹特性与2阶RC模型一致，可作为对2阶RC模型参数进行辨识的基础。

图2 电压回弹曲线

可根据2阶RC模型推导出电压回弹特性方程。放电结束后，RC网络为零输入响应，根据2阶RC电路模型，在BC段任意时刻的电压值为

以图中B点对应时刻，即放电结束下一采样时刻作为零时刻。

将上式简化为

根据式（3）～式（6）可知：

式中k0为电池静置至稳定状态的端电压值，即对应放电倍率和SOC下的开路电压值。

电池放电过程中，不同电流和SOC下电池RC参数辨识原理可描述为：通过将动力电池以不同的恒定电流放电至一定的SOC下，再静置至电池稳定，从而获得不同电流和SOC下电池回弹特性测试数据；基于测试数据，按式（3）～式（11）进行计算，从而获得不同电流和SOC下电池2阶RC模型参数。

2 电池特性测试

2.1 测试平台

采用动力电池，单体电池额定电压3.7V，额定容量2 900mA·h，最大放电电流10A，将8节电池并联作为一个电池组进行充放电试验。由于本研究侧重于参数辨识算法的验证，故仅采用放电工况进行测试与验证。

对电池放电特性测试采用某专用电池测试系统，如图3所示。通过系统配置的测试管理软件可对动力电池充放电测试流程进行编辑，实现自动化测试，还可实现对电池在充放电过程中的电流、电压等参数进行实时获取和记录。测试设备与控制电脑通过以太网连接，控制充放电通道工作，实现对动力电池组的充放电。

图3 试验测试平台

2.2 测试方案

电池RC参数随其充放电电流、SOC、温度的变化而变化，本应在不同温度下对电池在不同SOC和电流时的放电特性进行测试。但因不同温度下的测试和参数辨识过程基本相同，且本研究的主要目标在于验证基于模拟退火的参数辨识算法，故仅测试在某一温度下的数据。

以1.0C放电过程为例说明电池放电测试流程。试验开始后，首先采用先恒流后恒压的充电方式，将动力电池充满，此时动力电池组SOC为100%。将充满电的动力电池静置30min，使其达到稳定状态。然后以1.0C的恒定放电电流放电至SOC为0.9，静置30min，获得电池电压回弹特性；重复上述放电过程，但将电池放电至 SOC为 0.8，0.7，0.6，0.5，0.4，0.3，0.2，0.1，分别测取其电压回弹特性，获得电池在1.0C电流放电下，放电至不同SOC时的放电特性曲线。

图4 动力电池组电流、电压曲线

为进一步获取电池在不同放电电流下的特性曲线，分别以恒定放电电流0.25C，0.5C，0.75C，1.0C，1.25C，1.5C重复上述试验过程，即得到电池在不同放电电流下、不同SOC下的放电特性。将以上试验获取的所有“回弹曲线”数据导入模拟退火算法进行参数辨识，即可得到不同放电倍率和SOC下动力电池的RC参数。

3 基于模拟退火算法的电池参数辨识

3.1 模拟退火算法的参数辨识

根据前面的理论分析，欧姆内阻R0，极化参数和开路电压可分别按式（11）和式（6）进行辨识。对于式（6），在任意解 x=［k0k1τ1k2τ2］下，任意时刻都有唯一确定的y（t）与之对应。即在任意时刻都可由动力电池模型参数确定唯一的端电压值，因此可建立如下目标函数：

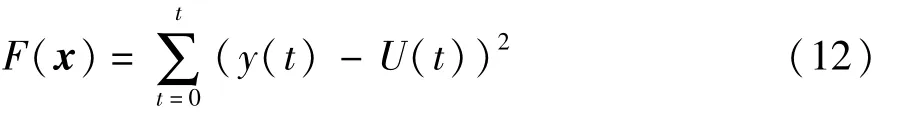
式中：y（t）为由模型参数确定的对应时刻端电压估计值；U（t）为回弹阶段对应时刻的端电压值。

将F（x）作为模拟退火算法的目标函数，在全局范围内搜索解x，求得F（x）的最优解。通过式（7）～式（10）即可求得当前电流和SOC下的模型参数。

模拟退火算法流程图如图5所示。

图5 模拟退火算法流程图

该算法基于对固体退火过程的模拟，用来控制算法的进程，最终求得组合优化问题的全局最优解。其中优化问题的一个解x及其目标函数F（x）分别对应于固体的一个微观状态i及其能量E（i）。算法控制参数T担当固体退火过程中温度的角色，对于T的每一个取值，算法采用Metropolis接受准则，持续进行“产生新解- 判断- 接受或者舍弃”的迭代过程而达到该温度下的平衡点［13］。通过在MATLAB中编写M文件实现算法，完成对动力电池参数的辨识。算法具体步骤如下。

（1）初始化 初始化退火温度T=500℃产生随机初始解 x=rand（1，5）每个温度下迭代次数 L=500。算法的实现虽然与参数的初始值设置无关，但根据经验确定初始值大致区间，可缩小算法的搜索范围，提高算法的收敛速度。根据锂电池的特性和试验数据可估计极化内阻R1和R2的值均为毫欧级，极化电容C1和C2的值在103～105F数量级之间。由于 x=［k0k1τ1k2τ2］，选取初始解 x=［4.2，I×10-3，0.5，I×10-3，0.5］，计算目标函数在 x时的函数值 F（x）。

（2）在温度T下重复执行如下操作，直至到达温度T的平衡状态。

a.在解x的邻域内产生新的可行解x′，即在当前状态的邻域结构内以正态分布产生，同时计算x′的目标函数值 F（x′）。

b.计算x′的目标函数F（x′）和x的目标函数F（x）的差值 ΔF。若 ΔF＜0，则接受 x′为当前的新解；否则，计算概率 p=exp（-ΔF／T），若概率 p＞random［0，1］，则接受 x′为当前的新解。其中，random［0，1］是区间［0，1］内的随机数。

c.判断是否达到迭代次数L，若未达到迭代次数，返回步骤（1），继续循环，否则跳出循环，执行退火操作。

（3）退火操作 首先判断是否满足算法终止条件（T=0），若未满足，执行降温操作：T=0.99T，然后返回步骤（2）继续循环，直至到达算法终止条件，其中0.99为降温系数C。若满足算法终止条件，则输出当前解为全局最优解，算法结束。

将动力电池以不同电流放电至不同SOC时静置的“回弹曲线”数据分别导入模拟退火算法，即可辨识得到动力电池不同放电倍率、不同SOC下的模型极化参数。

3.2 辨识结果与分析

3.2.1 极化特性“回弹曲线”的拟合

以0.5C电流将电池组放电至SOC为0.9，充分静置电池至稳定状态，将静置阶段的电压数据导入模拟退火算法，辨识结果如表1所示。

表1 极化特性“回弹曲线”参数辨识结果

将辨识得到的参数代入式（3）得到电压回弹估计值，估计值与试验值对比如图6所示。图6（a）表示电压回弹特性测试值与通过参数辨识的预测值对比，两条曲线基本重合。图6（b）反映两者的绝对误差，绝对误差最大为6.4mV，平均误差为1.647mV。该结果精度较高，说明模拟退火算法对模型极化参数有较高的辨识精度，辨识结果可很好地反映动力电池的极化特性。

图6 电压回弹特性测试值与理论模型估计值对比

3.2.2 不同SOC和电流下参数辨识结果

将试验中获得的不同电流和SOC下电压回弹特性数据分别导入模拟退火算法和式（11），辨识得到不同放电倍率和SOC状态下动力电池模型RC参数，结果如图7所示。

由辨识得到的结果可知，在不同放电倍率和SOC状态下动力电池模型参数的差异较大。可通过查表获取连续放电状态动力电池模型的参数，完成对模型参数的在线辨识，实现对电池状态准确估计。

4 仿真与试验验证

4.1 动力电池Simulink仿真模型

图7 不同放电电流和SOC下电池RC参数辨识结果

根据电路模型的状态方程和输出方程在MATLAB／Simulink中搭建动力电池仿真模型，如图8所示。

图8 动力电池仿真模型

模型以电流信号作为输入，采用安时积分法对动力电池的SOC进行实时估计。将实时电流和SOC导入模型参数模块，通过查表在线得到对应状态下的开路电压、欧姆内阻和极化参数，将其导入计算模块动力电池的实时端电压。其中查表模块的参数是在离线状态下，将动力电池以不同放电倍率放电至不同SOC状态下的静置“回弹曲线”数据导入模拟退火算法辨识得到。

将电池的工况试验电流值输入图8所示的2阶RC动力电池模型，通过对比工况测试的实时端电压和仿真的端电压数据，验证模型的合理性和模拟退火算法对参数辨识的准确性。

4.2 恒流放电工况验证

在恒流放电工况下对电池电压试验值和仿真值进行对比，该工况为：将动力电池组充满，静置至稳定状态，使其初始SOC为100%，以0.75C电流放电2 400s。该工况下仿真与测试结果对比如图9所示。

图9（a）为恒流放电工况仿真与试验结果对比，图9（b）为两者的绝对误差，图9（c）为两者的相对误差。从图中可以看出，仿真值与试验值绝对误差最大值为64.46mV，平均值为49.56mV，相对误差最大值为1.77%，平均值为1.35%，结果显示通过模拟退火算法对动力电池模型参数的辨识有较高的精度。

4.3 变电流工况验证

采用新欧洲行驶循环（new European driving cycle，NEDC）进行变电流工况仿真与试验验证。将NEDC工况转换为时间- 电流模拟工步，在图2所示的电池测试上对电池组进行NEDC工况下的充放电试验，获取电池在该工况下电压变化的测试数据。同时将NEDC工况输入电池模型，对电池在该工况下电压变化特性进行仿真。NEDC工况下仿真和测试结果如图10所示，为清晰展示数据对比结果，仅截取部分数据进行分析。

图10（a）为 NEDC局部电流 时间信号，图10（b）为电压试验值与仿真值的结果对比，图10（c）反映两者的绝对误差，图10（d）反映两者的相对误差。由图可见，绝对误差最大值为53.29mV，平均值为15.73mV，相对误差最大值为 1.5%，平均值为0.4%，对比结果表明模拟退火算法对动力电池的参数辨识有较高的精度。

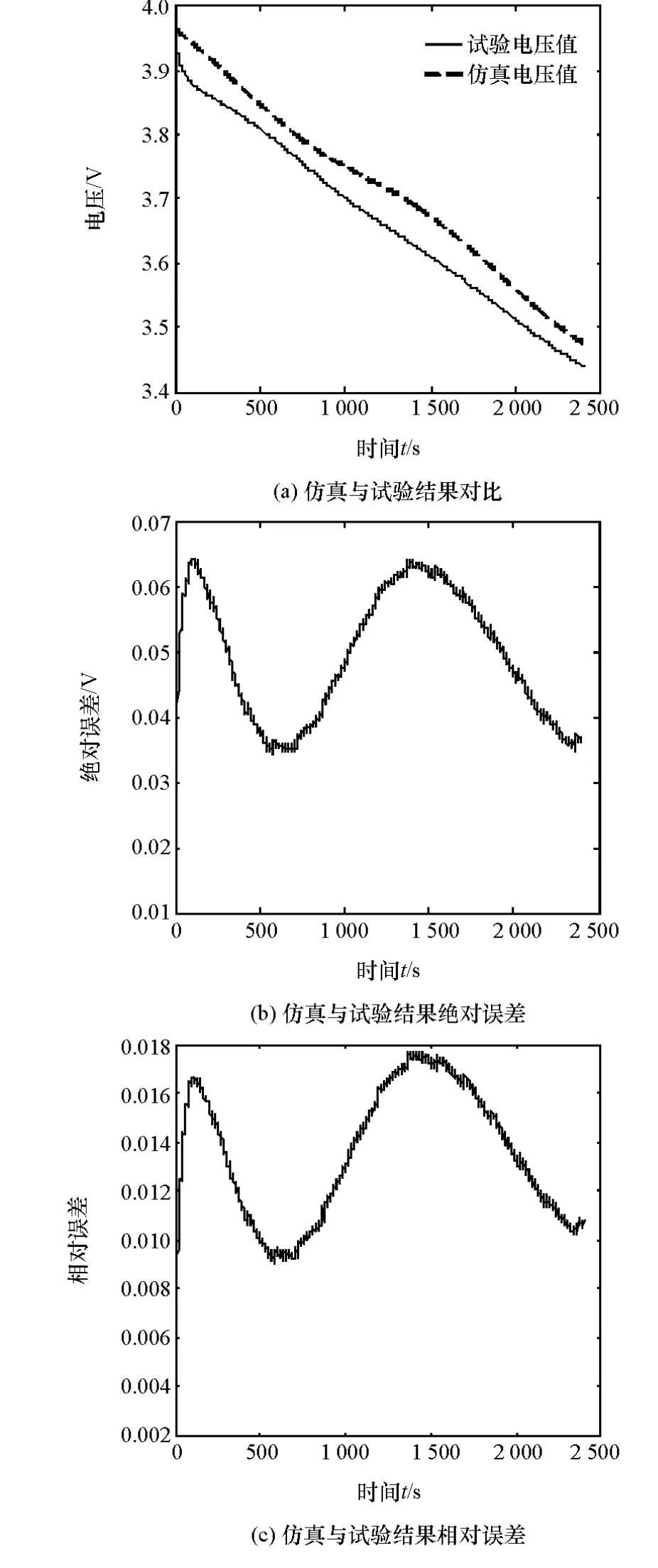
图9 恒流放电工况仿真与试验结果对比

5 结论

（1）通过建立电池2阶RC模型，并对其电压回弹特性进行分析，阐述采用电压回弹工况测试数据进行参数辨识的原理。在此基础上设计试验，对电池在不同放电电流和SOC下放电特性进行测试，获取不同工况下电压回弹数据。

图10 变电流工况仿真与试验结果对比

（2）采用模拟退火算法，用不同放电倍率和不同SOC下的“回弹曲线”测试数据进行参数辨识，得到电池模型在不同放电倍率和SOC状态下的RC参数值。恒电流放电和动态工况下仿真和测试结果说明，采用模拟退火算法对电池RC参数辨识具有较高精度，模型预测值与测试结果误差较小。

（3）本文的研究为相关工作奠定了良好基础，今后可在不同温度条件下重复本文的辨识工作，从而获得更为全面的RC参数在不同温度下随电流和SOC的变化特性。