一种代数曲线的C3连续性条件

孙明灿，师 晶

（闽南理工学院 信息管理学院，福建 石狮362700）

在计算机辅助几何设计中，单一的曲线曲面难以构成复杂的工业几何造型，因此，我们通常采用曲线曲面拼接的方法来满足实际需要。如何实现曲线间的光滑拼接已成为计算机辅助几何设计（CAGD）的重要研究内容。

样条插值方法是计算机辅助几何设计中重要的曲线构造方法［1］。如Bezier曲线和B样条曲线因其良好的几何性质和逼近性质，成为曲线曲面设计的有力工具，然而它们不能描述抛物线以外的圆锥曲线［2］。有理Bezier曲线虽能精确描述二次曲线曲面，但是存在求导、求积不方便的问题［3］。此外，NURBS曲线的权因子选择和参数化问题尚未完全解决，利用三角函数构造的曲线在局部调控曲线形状时不够灵活等［4-5］。这些缺点使得样条插值曲线在曲线曲面设计中无法完全发挥优势。

在本文中，我们研究了一种插值平面四点及两端点切线的三次代数曲线达到C3连续性的条件，分析了这种代数曲线的性质，得出了曲线间的连续拼接条件。

1 基础知识

给定R2中的四点及两端点P1、P4处的两条切线L1、L2，现构造一条三次代数曲线使其依次通过并且在端点P1、P4处的切线分别为 L1、L2。 设 L3是通过点 P2、P3的直线，L4是通过点 P1、P2的直线，L5是通过点 P3、P4的直线，L6是通过点P1、P4的直线，如图1所示。直线的方程为

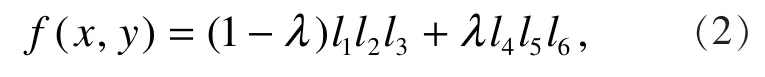
图1 三次代数曲线 ()Cλ

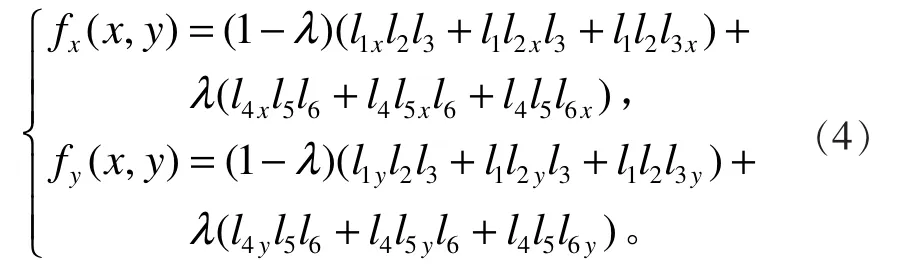
直线 L1、L4和 L6的交点为 P1， 直线 L2、L5和 L6的交点为 P4，故有

代入式（4），可得

2 曲线性质

1）端点性质：该曲线插值于首、末两端点，并且与控制三角形的两边相切，即

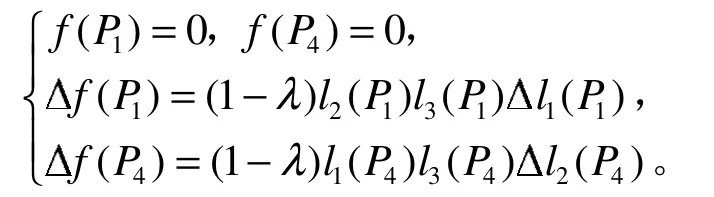
图2 取不同值时的代数曲线 ()Cλ λ

3 曲线的连续性条件

其次这两曲线在公共连接点处还应具有相同的一阶导数，即

此时直线L12与L21重合，即由引理2和式（8）可得

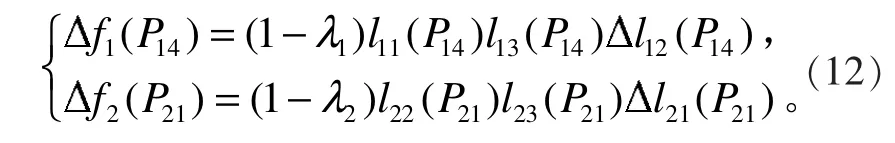
将式（10）和式（11）代入式（12），可得因此式（9）是曲线达到C1连续的充要条件。

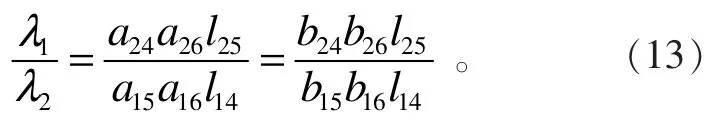
由引理 3及式（14）得

将式（6）和式（8）代入式（15），可得

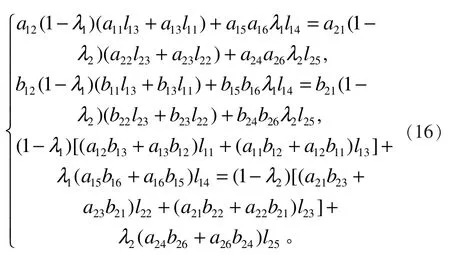
证明过程与定理2的证明过程类似。

4 计算实例

图3 部分花瓣图形及其控制三角形

图4 光滑拼接后的花瓣图形

图5 心形图形及其控制三角形

图6 光滑拼接后的四叶草图形

5 结束语

在本文中，我们通过分析一种插值平面四点及两端点切线的三次代数曲线的性质，得到了曲线达到C1、C2和C3连续的充要条件。利用该条件进行曲线间的光滑拼接不仅保持了原曲线的一些重要性质，而且通过适当选取形状参数可调整曲线的形状。给出的实例说明该方法在几何造型中具有较好的应用。