基于混合遗传算法的铁路物流中心布局研究
刘姣姣
(中国铁路设计集团有限公司 线站院,天津 300142)
0 引言
传统铁路货场向现代铁路物流中心(园区)转型是我国铁路货运组织改革的一项重要任务,物流中心除具备原有铁路货运站功能外,还将融入现代物流服务,吸引相关企业入驻,使传统的铁路货运功能得到增值。
传统的铁路物流中心包括货物仓储区、包装区、加工区、配送区、商贸业务区、公铁联运区、物流金融区、电子交易区、集装箱转运区等不同功能区。将它们按照一定的优化准则组合在一起,充分发挥各区域的功能属于一种布局问题[1-2]。
布局问题是NP-hard问题,由于布局问题的复杂性,在有限的时间内难以获得问题的精确解[3-4],所以绝大部分解决布局问题的算法是启发式的,在这些启发式算法中,遗传算法以其高效性、并行性和较好的鲁棒性在布局问题中得到了较为广泛的应用[5-6]。在国内,一部分研究者已将遗传算法应用于钢铁物流中心的内部规划[7-8]和铁路物流中心的布局研究[9-10]。
物流中心的最优布局依赖于优化模型的合理性和优化算法的高效性。传统的模型多以矩形为物流中心边界,并采用传统的遗传算法进行求解,假设其矩形边界缺乏对实际不规则边界的适应性,而传统遗传算法通常因早熟而易陷入局部最优解。为解决上述问题,通过建立能够考虑物流中心不规则边界条件的优化模型,在传统遗传算法中引入模拟退火局部搜索机制,以增强算法的全局收敛性,从而获得最优的、合理的物流中心布局。
1 铁路物流中心最优布局数学模型
1.1 最优目标的原则及优化模型
物流中心布局规划应当遵循以下原则[11]:①运输成本最小化;②功能区之间的联系最大化;③功能区之间不能重叠并保持一定的距离;④功能区应当在物流中心规划范围内。运输成本最优模型计算公式为

式中:F1为运输成本;dij为i到j的距离;gij为i到j运输物品的重量。
功能区之间关系最大化模型计算公式为

式中:目标函数将功能区之间关系最大化模型转换为最小化模型形式,F2为功能区之间的关系函数;V为功能区i与j的最大相邻关联度(取V= 4);Rij为i与j的相互关系,分为物流关系mrij和非物流关系nrij,通过权重系数α和β加权组成;非物流关系由与业务流程、组织管理和环境安全的nrij1,nrij2,nrij3通过权重系数w1,w2,w3组成;bij为广义距离相邻度[7]。
为了适应物流中心土地的实际情况,增强优化目标的灵活性,建立了考虑不规则边界情况的约束条件准则。根据功能区的特点,一般功能区均以矩形功能区为主,而园区土地边界可以考虑任意的边界形状。功能区变量示意图如图1所示,对于一个功能区而言,中心坐标 (xi,yi)、长度Li、宽度Wi和角度αi可惟一确定该功能区的位置和形态,第k个角点的坐标计算公式为


式中:θi1—θi4分别为功能区4个角点相对于X坐标轴正方向的角度。

图1 功能区变量示意图Fig.1 Sketch map of functional area variables
1.2 约束条件
模型需满足2个约束条件:①功能区之间不能重合;②功能区不得超出边界,其中边界通过连续坐标点表示。这2种约束条件可采用计算几何的射线法或面积法[12]从检验功能区i与功能区j的点面相对关系,以及功能区i与物流中心边界区域的点面关系予以判定。当满足上述2个边界条件时,罚函数置为0,否则,设置一个较大的罚数。此外,每个功能区的长度和宽度要保持一定的比例,即:λmin≤λi=Li/Wi180°≤λmax。按照归一化原则并考虑各种权重可将2个子目标函数组合成一个单目标函数。

式中:μ1,μ2分别为 2 个子函数权重系数,μ1+μ2= 1;归一化系数其中V含义同前,可取4;Np1,Np2,Np3分别为功能区相互重叠数目、功能区超出物流中心用地界的数目和功能区长宽比超出规定范围的数目。
优化目标函数的优化变量为xi,yi,αi,Li,Wi。优化目标函数同时覆盖了2个子优化目标,并同时考虑了边界约束条件。此外,还能够针对任意物流中心边界形状的情况进行优化。
1.3 算法设计
混合遗传算法将传统的遗传算法与模拟退火算法结合,发挥遗传算法泛化搜索和模拟退火算法局部精细化搜索的优点。为了避免Hamming悬崖问题[13],采用格雷码进行算法设计。
将模拟退火算法融入遗传算法,以遗传算法中的适应度比模拟退火算法中的内能,将执行遗传操作之前的种群作为模拟退火算法的输入解,对该输入解进行遗传操作产生新解(即遗传算法的新个体),并利用Metropolis抽样法则对新解进行抽样。在算法搜索初期,解的分布范围比较广,且目标函数的曲面上分布较多局部峰谷,对适应度较低的解,接受概率比较大。在搜索后期,逐步逼近全局最优,接受适应度较低解的概率应当趋于0。
在整个算法过程中,遗传算法的进化代数与模拟退火的温度进程统一为一个循环控制参数,使得每次遗传算法操作均发生在模拟退火算法的某一温度下,具体算法如下。
(1)设置各项参数,随机产生初始种群。
(2)评价初始种群的个体适应度,将高适应度的个体作为父代种群。
(3)父代种群根据设定的交叉概率和变异概率执行交叉和变异操作产生子代。
(4)根据进化代数,确定相应的模拟退火温度,执行模拟退火局部搜索,保留优秀个体。
(5)检验结果是否收敛,若收敛则输出最优解并结束搜索,否则转(2)。
1.4 算法检验
通过搜索经典有解析解的Schaffer函数的最大值来检验所设计混合遗传算法的有效性。该函数全局最大值为1 (x= 0,y= 0),在全局最高点附近有一圈局部次高点,其对应的值约为0.990 28,其函数表达式为

混合遗传算法的控制参数设置如下:最大进化代数200,种群规模200,交叉概率0.7,变异概率0.05,初始温度10 000。函数图像如图2所示,测试函数寻优收敛曲线如图3所示,测试函数优化结果如表1所示。在图3中,以解的变化曲线表示每一代群体中最优秀得个体,用均值表示每一代群体的总体情况,由于函数的多峰值性,搜索前期震荡较大,在前75代左右解的收敛曲线呈阶梯形上升,目标函数值由0.995跳到无限接近1的位置,同时均值收敛曲线斜率增大,收敛速度加快,与解的收敛曲线几乎重合,快速稳定地收敛到全局最优解,说明该算法具有很强的全局搜索能力。

图2 函数图像Fig.2 Function images
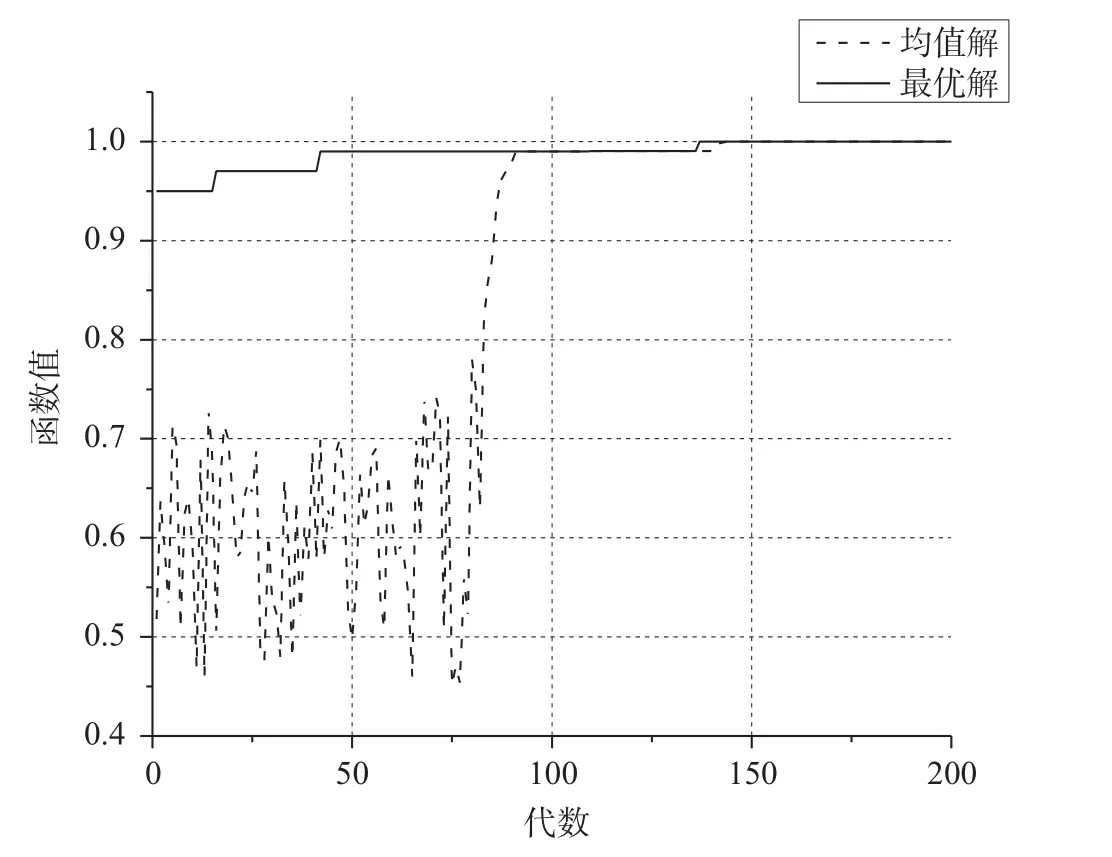
图3 测试函数寻优收敛曲线Fig.3 Test function optimization convergence curve

表1 测试函数优化结果Tab.1 Test function optimization results
2 实例分析
某铁路物流中心规划总占地1 200 000 m2,由于市政规划道路的分割和地形条件的限制,可被用作物流中心的用地边界通常是不规则的。物流中心包括仓储区、保税区、配送区、流通加工区、交易展示区、办公生活区、集中停车区7大功能区。各功能区规划用地面积如表2所示,各功能区之间日均物流量如表 3所示,各功能区之间综合物流关系如表 4所示。

表2 各功能区规划用地面积 m2Tab.2 Planning area of each functional area

表3 各功能区之间日均物流量 tTab.3 Daily average volume of flow between each functional area

表4 各功能区之间综合物流关系Tab.4 Integrated logistics relationship among functional areas
通过优化模型以及混合遗传算法的优化求解方法,所得到的最优物流中心总布置如图 4所示。由图 4中可知,物理中心布局中将停车场沿用地界的斜边布置,这样可以节省场地并满足用地需求,同时距离关系紧密货运量大的仓储区、配送区和流通加工区较近,交易展示区和办公生活服务区位于左下角,最大程度实现了物流中心的优化配置。
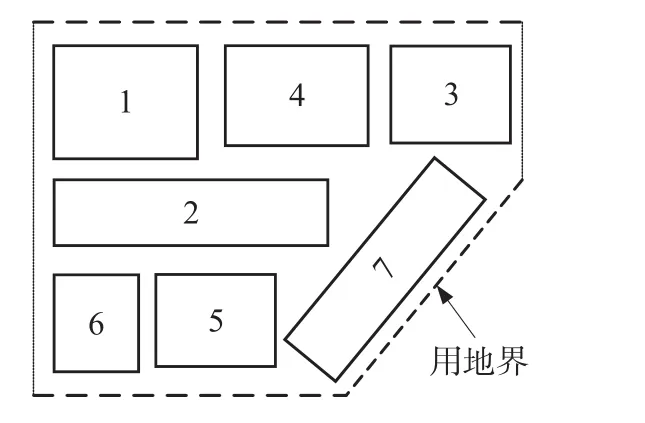
图4 物流中心总布置图Fig.4 General layout of logistics center
3 结论
针对不规则物流中心的优化目标函数,引入了局部搜索能力较强的模拟退火算法,形成了物流中心布局最优化的整套解决方案,并对某物流中心进行了布局的优化,主要结论如下。
(1)提出可以适应于不同边界形状物流中心用地的优化算法,同时在功能区的空间优化目标函数中引入了转动自由度,以适应不规则边界的功能区布局问题。
(2)将传统遗传算法与模拟退火算法相结合,增强优化方法的全局收敛性,保证了优化求解的精度。
(3)物流中心的最优布局取决于优化目标函数的合理性以及求解方法的高效性,所建立的目标函数能够很好地考虑实际物流中心规划中遇到的用地形状问题,同时算法本身具备很强的全局搜索能力,因而有更广泛的实用性。
(4)为物流中心的布局提供一种方法,为后续的物流中心设计提供一个理论的最优布局方案,在实际应用中,仅需要根据实际情况进行局部修改和调整即可形成最终的物流中心布局方案。

