g支配策略的MOEA/D算法求解多目标流水车间调度问题

陈世翔，朱光宇，徐文婕

(福州大学机械工程及自动化学院，福建 福州 350108)

0 引言

流水车间调度问题(flow-shop scheduling problem，FSP)是一类重要的生产调度问题，有广泛的工程应用背景[1].调度优化算法可分为数学规划方法、规则调度方法、仿真调度方法、启发式方法和智能优化方法等[2].智能优化方法包含遗传算法、禁忌搜索算法、模拟退火算法、蚁群算法和粒子群算法等.如： 文[3]提出变邻域改进遗传算法求解混合流水车间调度问题.文[4]应用并行禁忌搜索算法来解决混合流水车间调度问题.文[5]应用改进的免疫模拟退火算法求解混合流水车间调度问题.文[6]改进离散粒子群算法求解柔性流水车间调度问题.该类智能优化方法无需问题的特殊信息，可以很快收敛到局部最优并获得近似最优解.

基于分解的多目标进化算法(multi-objective evolutionary algorithm based on decomposition，MOEA/D)是一种将传统的数学规划方法与进化算法相结合求解多目标优化问题的算法[7].由于其简单性和优越的性能得到了学者广泛的关注.Zhang等[8]在MOEA/D中引入DE算子，有效地解决了Pareto前沿问题.Ishibuchi等[9]针对MOEA/D中采用两种不同聚合函数，降低了选择聚合函数的难度.郑金华等[10]提出了一种基于权重迭代的偏好多目标分解算法来解决参考点的位置信息对算法的影响.模糊Pareto支配概念的引入提高了算法的收敛速度[11].Chang等[12]提出MOEA/D算法在流水车间调度问题中的应用，并讨论了MOEA/D算法在本问题中所采用的分解方法，通过实验证明，MOEA/D算法在二维或三维流水车间调度问题上比NSGA II和SPEA 2效果更优.MOEA/D将一个多目标问题(MOP)按照一定的权重分解为若干个单目标优化子问题，然后优化这些单目标子问题，具有收敛速度快，效率高等特点，但是在求解流水车间调度非凸MOP时会面临解的质量不够高、分布性差等问题[13].

本研究将g支配思想[14]引入MOEA/D算法中，结合基于二范数权重向量，提出g支配策略的MOEA/D算法(g-MOEA/D算法).g支配把传统Pareto前沿与参考点的使用相结合，使基于分解的多目标进化算法生成适应决策者偏好的有效解的集合，来代替整个Pareto解集或单个有效解，从而提高MOEA/D的择优效果及收敛性.实验表明，g支配可以与 MOEA/D算法有效结合，获得很好的多目标优化解，算法在各性能指标上也能达到令人满意的结果，可有效解决流水车间调度问题.

1 流水车间调度模型的构建

1.1 问题描述

FSP作为典型的工业生产规划问题是当前学术界的热点问题之一.FSP从数学上可以描述为：n个不同的工件在m台不同的机床上加工，每个工件都以固定的顺序依次访问所有的机器，每个工件在不同机器上的加工时间都是固定的[15].这里使用时间矩阵T来表示使用机器加工零件的时间，其中：tij∈T，表示第i个工件使用第j个机器的加工时间[16].

1.2 多目标流水车间调度模型构建

本FSP调度任务是确定各个工件的加工次序，即以工件的加工顺序代表种群个体，其目的是同时优化最大完工时间、最大延迟时间及库存成本三个目标[17]，该问题优化后得到一组解集而不是一个最优解，即得到Pareto最优解集.针对本问题，构建目标函数：

minY=(f1,f2,f3)

(1)

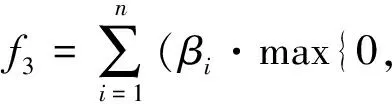
FSP问题约束条件如下： ① 每个工件加工路径相同，不允许改变(依序从机器1到机器m加工)； ② 每个时刻，每台机床只能加工一道工序, 工序不允许中断； ③ 一个工件不能同时在不同机床上加工； ④ 工序的准备时间忽略不计，或者包含在加工时间中.构建时间约束条件：

C11>t11

(2)

Cik≥max{Ci(k-1),C(i-1)k}+Tik(i=2, …,n；k=2, …,m)

(5)

式(2)表示工件1第一道工序的加工时间大于在第一台机器加工时间，式(3)～(5)表示对任何工件，其完成时间取决于其在某机器上的加工时间和开始时间.其中：Tik表示第i个工件使用第k台机器的加工时间；Cik为工件i的第k道工序的完工时间.

2 MOEA/D算法描述

多目标优化问题数学模型描述如下：

minF(x)={f1(x),f2(x), …,fi(x), …,fm(x)}T, subject tox∈Ω

(6)

其中：x是决策变量；Ω是决策空间；F:Ω→Rm为m维目标向量；Rm表示目标空间；fi(x)是第i个待优化的目标函数；F(x)为所得目标函数值.

MOEA/D算法实现方式是将多目标优化数学模型(式(6))通过聚合函数分解成一系列单目标子问题, 利用子问题的函数值，在种群更新过程中通过对比父代、子代所得子问题函数值的大小，保留子问题函数值较小的种群，实现对种群的更新，最终获得一组Pareto最优解.算法主要涉及分解策略、父代个体选择策略和外部存档更新策略.

2.1 分解策略

MOEA/D聚合函数的分解策略主要有三种[18]: 加权求和聚合法(weighted sum approach), 切比雪夫聚合法(Tchebycheff approach)以及边界交叉聚合法(boundary intersection approach).切比雪夫聚合法在求解二维或三维目标优化问题上具较好的优化能力，因此主要讨论切比雪夫聚合法，应用切比雪夫聚合函数将多目标模型(式(6))转化为单目标子问题的形式如下：

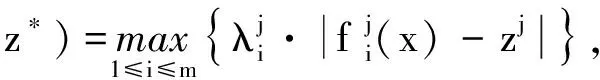
(7)

2.1.1 权重向量产生方法

MOEA/D通过权重向量的选取对种群中的个体运动轨迹和搜索方向进行控制.能够自适应地调整对Pareto前沿不同部分的搜索.MOEA/D使用NBI(normal boundary intersection)法在超平面上产生均匀分布的权重向量[22].NBI法在种群规模大、目标多时，存在权重向量分布不均匀的问题.为改善MOEA/D在FSP问题上的应用，提高MOEA/D的性能，采用基于二范数的方法生成权重向量：

(8)

(9)

2.1.2 理想参考点选取方法

切比雪夫聚合函数中理想参考点的初值取初始种群中各个子问题目标函数的最小值.表示为：zj=min{fj(x)|x∈Ω}，j=1, 2, …,M.在每次种群更新后，比较更新后的目标函数值与上一代的理想参考点函数值，保留其较小值，完成对理想参考点的更新.具体步骤可表示为： 若zj>fj(y′), 则设zj=fj(y′),j=1, …,M.y′为更新后的个体，fj(y′)为第j个目标的函数值.

2.2 父代个体选择策略

MOEA/D算法中，从父代中选择两个个体进行交叉从而对个体进行更新.通过父代个体的邻域关系选择出两个个体.计算个体权重向量之间的欧式距离，欧式距离越小，说明个体之间的函数值越接近.取函数值最接近的两个个体进行交叉，有利于对种群的进化.其具体方法可表示为：

计算权重向量集{λ1,λ2, …,λi, …,λN}之间的欧式距离.其中，λi为个体i所对应的权重向量；

选取与λi欧式距离最近的T条权重向量{λi1, …,λiT}，得到T条权重向量所对应的个体，将其作为个体i的邻域集B(i)={i1, …,iT}.其中，T是权重向量的领域个数.依靠这种邻域关系，选定父代个体进行交叉、修正操作，繁殖出新后代，实现个体更新.

2.3 外部存档更新策略

MOEA/D算法中使用聚合函数对种群进行一次更新后，采用非支配关系筛选出Pareto最优解作为外部存档(EP).每次迭代后都对外部存档进行更新.具体方法为： 将EP中所有被F(x′)支配的向量移除, 将非支配F(x′)加入EP中，完成对EP的更新.其中，x′为更新后的新解.F(x′)为其对应的目标函数值.

3 g-MOEA/D算法及求解FSP

3.1 g-MOEA/D算法描述

经仿真实验表明, MOEA/D算法的支配关系在求解流水车间调度MOP时，求解质量难以保证，解集的均匀性和分布性相对较差.将g支配策略作为外部存档更新策略引入MOEA/D算法，建立g-MOEA/D算法，新策略不但能与切比雪夫分解策略有效结合，而且能进一步提升求解多目标流水车间调度问题解的质量，能有效提升种群的均匀性及分布性.g-MOEA/D算法的实现方法为：

1) 初始化及建立外部存档EP.随机生成初始种群，设置EP上限NA，计算初始种群中个体g支配数量并进行降序排列，保留种群中前NA个个体，加入外部存档EP.

2) 应用切比雪夫聚合函数对多目标模型进行分解.

3) 利用权重向量从父代中选择个体，进行交叉、修正操作，繁殖出新后代，比较父代与新后代，实现个体更新.

4) 基于g支配的外部存档更新.合并更新后种群与父代外部存档EP，计算合并后种群中每个个体g支配数量并进行降序排列，保留种群中前NA个个体，加入EP，实现更新.

3.2 g支配策略

g支配(g-dominance)是对Pareto支配概念的改进，这种支配方法可在不使用任何标量函数的情况下，缩小已得到的Pareto解集范围，从而得到更为有效的解集.g支配的数学模型如下:

(10)

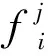
图1 基于参考点g的Flags值Fig.1 Flags based on reference point g

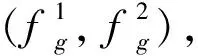
1) Flagg(fl)>Flagg(fn)；

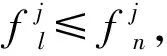
通过上述g支配的条件，可得知在Flagg(fi)=0区域的个体定由Flagg(fi)=1区域的个体所支配.因此g支配数量较多的个体主要分布在区域二及区域四中.在经过MOEA/D算法得到一组Pareto前沿后，结合g支配的条件，将进一步缩小Pareto前沿的有效解范围.在这两个区域中有效解集的分布(图2、图3中红色部分)主要分为两种情况.

由图2可以看出，参考点g并不是最优解.存在Pareto前沿上个体都比参考点g小的情况.因此有效的最优解集主要分布在区域四； 由图3可以看出，参考点g是理想的最优解.因此寻找区域二中与参考点最接近的个体作为更有效的最优解集.无论给定的参考点g是否比Pareto前沿更好，都能够通过g支配策略得出更为有效的最优解集.

图2 不可行的参考点 图3 可行的参考点

3.3 g-MOEA/D算法求解FSP的具体步骤

步骤1 设置参数，包括种群大小N； 邻域数量T； 目标个数M； 最大迭代次数maxgen； 外部档案上限NA.

步骤 2 利用式(12)产生N条权重向量λ1,λ2, …,λN.计算任意两权重向量的欧式距离，为每个向量选出与其距离最近的T个向量作为其邻域向量.对每个个体i=1, …,N，设置i的T条邻域B(i)={i1, …,iT}，其中{λi1, …,λiT}是个体权重λi的T条最小距离权重.

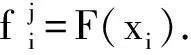
步骤4 对种群进行更新操作：

步骤4.1 交叉.从个体邻域B(i)中随机选择2个个体进行二进制交叉, 生成新个体y.

步骤4.2 修正.通过ROV将新个体y转化为整数型个体y′.

步骤4.3 更新理想参考点z.若zj>fj(y′), 则设zj=fj(y′),j=1, …,M.

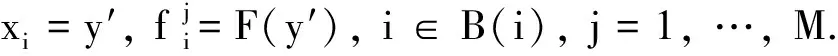
步骤5 外部存档维护和更新.采用g支配方法将EP中所有被F(y′)支配的解从EP中移除； 若F(y′) 不被EP中的任意解支配，则将非支配F(y′) 加入EP.

步骤6 如果满足停止条件(迭代次数大于maxgen), 则停止迭代, 并输出EP.否则, 返回步骤4.

4 实验结果与分析

4.1 实验设置

为验证g-MOEA/D算法的有效性及其优越性，采用文[19]的方法建立10个不同规模的流水车间调度实例.对g-MOEA/D算法与文[6]中MOEA/D算法在理想解、性能指标等方面进行比较.两算法对每一实例独立运行10次，采用当代距离GD[24]、间隔距离SP[25]来比较解集的收敛性和分布性.

4.2 进化算法的性能评价指标

1) GD指标.GD指标用于度量两种比较算法得到的近似Pareto前沿和真实Pareto前沿之间的距离，是算法收敛性的度量指标.GD指标定义为：

(11)

其中：P*为均匀分布的真实Pareto前沿；A是通过算法得到的近似Pareto前沿;v为从A中取任一近似Pareto前沿;d(v,P*)是v与P*的欧式距离的最小值; |A|是A中所有元素的总数.GD值越小，算法所求得的近似Pareto前沿与真实Pareto前沿更近，收敛性更好.

2) SP指标.SP指标用于评价算法的分布性，表示为：

(12)

其中：A是通过算法得到的近似Pareto前沿，|A|是A中所有元素的总数.该指标越小，所求的Pareto前沿的分布性越均匀.

4.3 结果对比及分析

以两种算法计算每个实例，并独立运行10次后得到多目标Pareto最优解的平均值、GD指标和SP指标的平均值，结果列于表1.

表1 多目标流水车间调度问题的仿真实验结果及其评价指标

两个算法的理想解为在各自的选择交叉过程中所得到的不同理想参考点.从表1可见： 在实例1, 2, 3, 4, 5, 6, 10中，g-MOEA/D算法的Pareto最优解在三个目标上全优于MOEA/D算法； 在实例7, 8, 9中，g-MOEA/D算法的Pareto最优解有两个目标优于MOEA/D算法.结果表明，g-MOEA/D算法所得的Pareto最优解总体上优于MOEA/D算法.

从表1的评价指标还可以看出： 其当代距离(GD)及间隔距离(SP)方面g-MOEA/D都小于MOEA/D算法，可见g-MOEA/D其解的收敛性和分布均匀性均要优于MOEA/D算法.

两种算法的GD指标及SP指标盒图如图4所示，用于分析算法的显著性差异，由于论文长度限制，图4仅给出了代表种群规模小中大的三个实例.盒图中间的红色横线代表中位数，红色“+”为异常点，盒图形状越扁表示方差越小，稳定性越高.从图4可见：g-MOEA/D算法所得盒图的中位线及上下两条横线的位置明显低于MOEA/D算法，说明g-MOEA/D算法其GD指标及SP明显低于原MOEA/D算法，所得解集质量更优.实验表明，基于g支配策略的MOEA/D算法可以有效解决多目标流水车间调度问题.

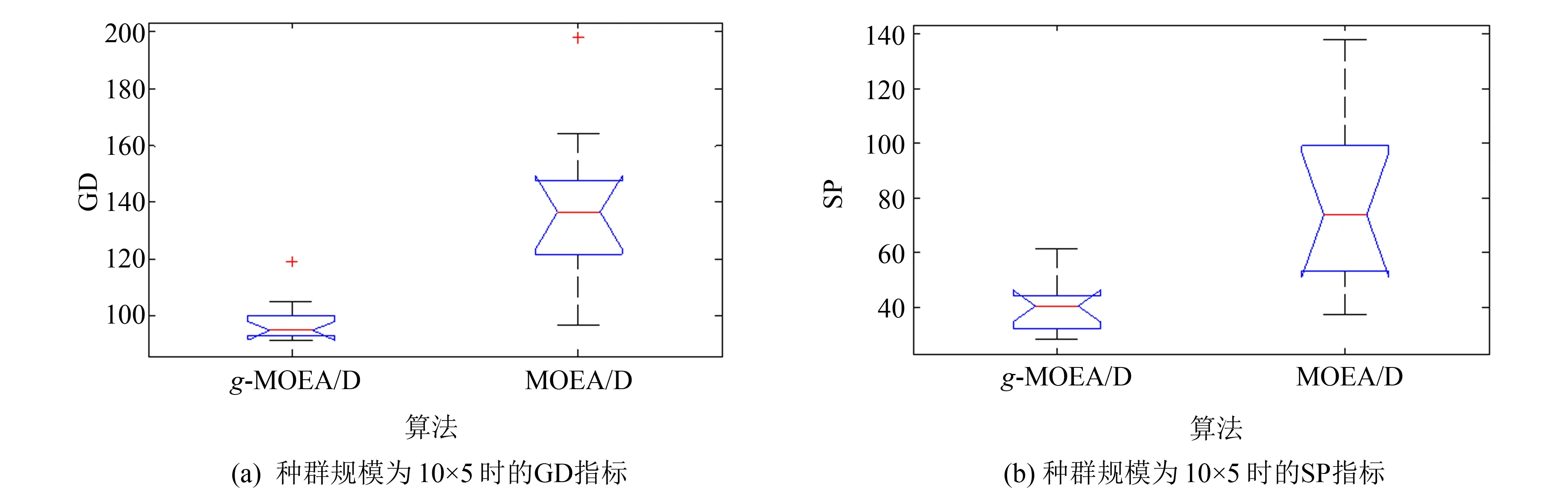
图4 两种算法在3种不同种群规模上运行10次的GD及SP指标盒图Fig.4 Boxplot of two algorithms for GD and SP running 10 times on 3 different population sizes

5 结语

为改善MOEA/D算法种群的收敛性与多样性，提高多维目标流水车间调度问题中解集的整体质量，对MOEA/D算法进行改进，提出一种g支配策略的MOEA/D算法.该算法采用基于二范数权重向量，并将g支配方法引入到MOEA/D算法中用以求解三维多目标流水车间调度问题.应用g支配方法可以提高外部档案择优的效率，进而提高解集的收敛性与均匀性, 得到较高质量的多目标优化解.通过仿真实验证明: 改进后的g-MOEA/D算法对FSP问题具有更强的求解效果.本算法仅针对流水车间调度问题进行求解，下一步将尝试考虑更高维度的多目标调度问题以及与其他类型的组合进行问题研究，如柔性作业车间调度问题、零空闲流水车间调度问题、无等待流水车间调度等.