扩底桩材料参数对其抗拔承载力影响分析

于海涛 徐强胜

（1.吉林化工学院 吉林省吉林市 132022 2.国网辽宁省电力有限公司经济技术研究院 辽宁沈阳 110015）

目前对扩底抗拔桩的理论研究远远滞后于工程发展的需要，对扩底抗拔桩的理论研究还不深入。本文采用数值模拟方法，根据现有的一些试验数据及工程实测资料，建立了合理的三维有限元计算模型，综合考虑了桩-土之间相互作用、土体初始应力与弹塑性等各种复杂因素，模拟了扩底桩的上拔过程。分析了材料参数对抗拔承载力的影响。

1 有限元模型的建立

以有限元软件ANSYS12.0为工具，采用轴对称方法进行模拟。桩、土均采用二维八节点的实体单元（solid45）模拟；土体为DP材料；桩与土体界面处设置接触单元CONTAC173和TARGE170来模拟桩-土之间的滑动和开裂，选用库仑摩擦类型。本文的计算区域径向取9倍桩径，桩底取2.5倍桩长；在该区域底部与外侧边界全约束，轴对称处仅约束X向位移。

2 扩底桩上拔行力的模拟

①初始地应力场的模拟：桩、土区域均使用土体参数、桩-土界面设置接触单元，通过对有限元模型施加重力场来模拟天然土体的初始应力。②成桩状态的模拟：桩、土区域使用各自参数、桩-土界面设置接触单元，用EKILL命令杀死接触单元，再利用EALIVE命令激活被杀死的单元，然后施加自重模拟成桩过程中产生的位移场。③上拔过程模拟：用EKILL命令杀死接触单元，再利用EALIVE命令激活被杀死的单元，然后施加自重及上拔荷载求解桩顶位移，求得的桩顶位移减去第二步中成桩所产生的桩顶位移，便得到上拔荷载下的桩顶位移。

3 材料参数对抗拔承载力的影响

3.1 扩底桩弹性模量的影响

以斜坡地形上平头扩底桩为基础，取桩长H=5m，d=1.2m，D=2.5m。扩底桩弹性模量按EP=10GPa、30GPa、100GPa分成三种工况，桩的形状和结构尺寸不变，其他材料参数不变。分别对对应于上述不同工况的扩底桩进行三维有限元分析，得到Q-S曲线如图1所示。

根据图1知，桩的上拔承载力随着桩体的弹性模量的增加而增大，但幅度很小，基本可以忽略不计。这是因为土体先因整体失稳而破坏；土体发生破坏时，桩身远未达到强度极限强度。以斜坡地形上平头扩底桩为基础，取桩长H=5m，d=1.2m，D=2.5m。土体弹性模量按ES=60MPa、120MPa、150MPa分成三种工况，桩的形状和结构尺寸不变，桩和土的其他材料参数不变。对不同工况的扩底桩进行三维有限元分析，得到Q-S曲线如图2所示。

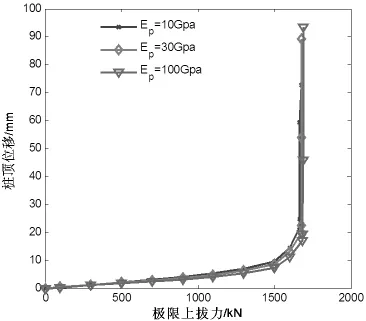
图1 不同桩体弹性模量的荷载-位移曲线

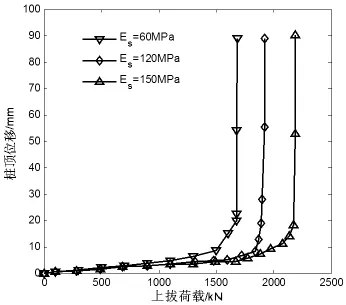
图2 不同土弹性模量下的Q-S曲线

从图像中可以看出土弹性模量越大，桩的抗拔承载力也越大。

3.2 土体粘聚力和内摩擦角的影响

以斜坡地形上平头扩底桩为基础，取桩长H=5m，d=1.2m，D=2.5m。土体粘聚力按c=20kPa、30kPa、40kPa、50kPa分成四种工况，保持桩的形状和结构尺寸不变，桩与土的材料参数不变。分别对对应于上述不同工况的扩底桩进行三维有限元分析，得到Q-S曲线如图3所示。另外，将上述不同土体粘聚力下桩的极限抗拔承载力值绘于图4。

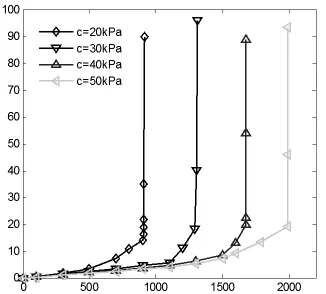
图3 不同土粘聚力的Q-S曲线

图4 承载力随土粘聚力的变化曲线

从图3和图4可以看出，随着土体的粘聚力的增加，扩底桩的抗拔承载力也增加。并且扩底桩的抗拔承载力随粘聚力的增大几乎呈线性增大。

以斜坡地形上平头扩底桩为基础，取桩长H=5m，d=1.2m，D=2.5m。土体内摩擦角按 φ=9°、18°、27°、36°分成四种工况，保持桩的形状和结构尺寸不变，桩与土的材料参数不变。分别对对应于上述不同工况的扩底桩进行三维有限元分析，得到Q-S曲线如图5所示。另外，将上述不同土体内摩擦角下桩的极限抗拔承载力值绘于图6。

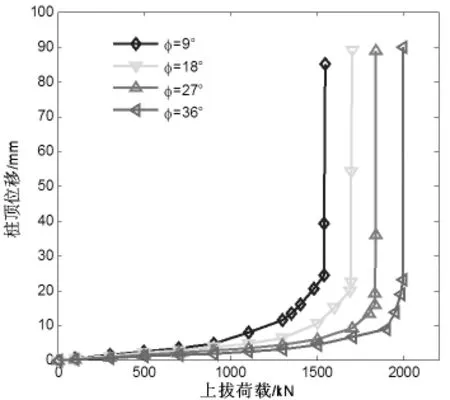
图5 不同土内摩擦角的Q-S曲线

图6 承载力随土内摩擦角的变化曲线

从图5和图6可以看出，随着土体的内摩擦角的增加，扩底桩的抗拔承载力增加。并且扩底桩的抗拔承载力随内摩擦角的增大几乎呈线性增大。

这两方面的原因也是显而易见的。土体的粘聚力和内摩擦角是构成土体强度的重要因素。土体粘聚力和内摩擦角的增大，意味着土体强度越大。因此，桩的极限承载力也就随之增大。

4 结论

①斜坡地形中，土弹性模量越大，扩底桩的抗拔承载力也越大。②斜坡地形中，土体的粘聚力和内摩擦角是构成土体强度的重要因素。土体粘聚力和内摩擦角的增大，意味着土体强度越大。因此，桩的极限承载力也就随之增大。