分组加权t-SNE的手写数字奇异类样本聚类方法研究

杜 芬，王 彬，薛 洁，龙雨涵，刘 辉，熊 新

1(昆明理工大学 信息工程与自动化学院，昆明 650500)2(云南警官学院 信息网络安全学院，昆明 650223)

1 引 言

随着人机交互和图像识别技术在生活中的广泛应用，数字手写体的识别问题得到了越来越深入的研究.由于不同文化、不同个体有不同的书写习惯，即便是同一个人，由于书写环境、书写方式等外界因素的不同，都可能导致书写结果的不一致，这使得每个手写体数字所呈现的特征是多种多样的.图1是从MNIST数字手写体数据库中选取的手写体数字样本，可以看出虽然相同数字的主要特征相同，但不同数字手写体样本即便是代表相同数字，在外形上可能还是存在较大的差异，这类与标准数字写法相差较大的手写体数字样本我们称之为奇异样本，奇异样本的识别是手写体数字识别中的难点问题.

为了得到更好的识别效果，近年来很多学者采用机器学习的方法对数字手写体识别问题展开了深入研究，2012年Ciregan D等人将卷积神经网络(Convolutional Neural Network，CNN)的方法应用于美国邮政服务提供的手写邮政编码数字的识别[1].2013年Dan Z和Xu C提出用反向传播(BackPropagation，BP)神经网络的方法对手写体数字进行特征提取[2]. 2015年J Schmidhuber提出结合卷积神经网络(CNN)和支持向量机(Support Vector Machine，SVM)[3]的混合模型在MNIST数字数据库中进行手写体识别[4].周菲菲等采用改进的方向特征提取方法与BP神经网络分类器相结合，提高了数字手写体的识别率，同时降低了拒识率[5].许洁等构建了一种基于稀疏保持典型相关分析的特征提取算法，在融合信息的同时还可以过滤冗余信息，提高了手写体的识别精度[6].采用支持向量机、BP算法、卷积神经网络等方法展开的手写体数字识别，其主要思想是通过构建机器学习模型和海量的训练样本数据，学习更有用的特征，从而提高手写体数字预测的准确性.尽管以上研究通过对超大量样本取得了较高的识别率，但由于奇异样本在主要特征上的差异，使得此类样本成为了影响样本识别率的主要因素，因此本文专门针对提高这类奇异样本的识别问题展开了研究.

由于上述数字手写体奇异样本的特征与常规数字手写体的样本差别较大，且时间复杂度高，因此使用机器学习方法难以准确的预测，因此本文拟采用降维的方法提取其主要特征并直接映射到二维空间内，通过分类完成数字手写体的识别.目前主流的线性高维降维方法如局部线性嵌入(Locally Linear Embedding，LLE)[7，8]、主成成分分析(Principal Component Analysis，PCA)[9，10]等已被应用于数字手写体的识别中，1997年Hinton G E等人用PCA方法对手写数字图像流形的建模方法进行研究[11]；2006年Chang H和Yeung D Y对手写体数字提出了鲁棒局部线性嵌入(RLLE)的方法[12，13]；2015年Phan N H和Bui T T T提出了一种使用PCA、小波变换和神经网络组合的手写字符识别算法[14].相对于线性降维算法，非线性降维方法能更好地发掘隐藏在高维数据中的流形分布[15]，其中t 分布随机领域嵌入算法( t-distributed tochastic neighbor embedding，t-SNE)[16]是由G Hinton于2008年根据2002年Hinton和Rowei所提出的SNE算法[17]进行改进并提出的新算法，并应用于数字手写体问题中.

图1 不同人书写的手写体数字0-9Fig.1 Handwritten numerals 0-9 written by different people

t-SNE算法是用高斯核函数计算高维联合概率，得到高维相似度距离，通过t-分布核函数定义低维空间内嵌入样本的相似度，并用梯度下降法的方法进行KL散度( kullback- leibler divergence，KL)的寻优计算，从而找到原高维空间和嵌入低维空间内尽可能相近的联合概率分布.由于高维空间内变量间的复杂非线性关系，这种单纯使用欧式距离来衡量样本相似性的方法并不能如实反映样本在高维空间真实的分布情况.为了使样本的主要特征能更好地保留下来，降低高维空间的信息在降维后的损失，可以对欧式距离进行分组加权处理.2013年Singha J等人对印度语言识别使用特征值进行加权欧几里德距离分类进行研究[18]；2014年Liu H C等人使用模糊混合加权欧氏距离进行失效模式和效应的分析[19]；2017年詹威威等人提出了自适应加权t-SNE算法应用在脑网络状态观测矩阵降维中[20].

文中以提高数字手写体中的奇异样本识别率为主要目标，提出了一种分组加权欧式距离的t-SNE算法，该算法通过分析手写体数字在高维空间中分布紧密关系的不同，将其分组加权，并构建新的高斯核函数计算其高维联合概率以及高维条件相似度距离，从而得到新的低维映射关系.基于MNIST公开测试数据库中奇异样本的实验结果显示，本文算法比t-SNE算法获得了更好的聚类效果，且查全率(Recall Rate)平均可提高4%，查准率(Precision)平均可提高3.3%，为奇异样本手写体数字的识别问题提供了一种新的解决方案.

2 分组加权t-SNE手写体数字降维算法

2.1 基本原理

t-SNE算法是将高维空间中样本对之间的欧氏距离转化为高维联合条件概率，同时计算低维空间内样本对的联合概率，并用KL散度构建目标函数，通过梯度下降法求取低维表达最优解.

在传统的t-SNE算法中，欧式距离表征两个空间向量之间的累积差异，并没有考虑对应单个元素之间差异的影响.如果直接将欧式距离用于特征向量之间的相似性度量，其度量精度存在较大的误差，因为它忽略了特征向量中对应数字手写体元素之间相似性的影响[21].本文拟采用一种分组加权的t-SNE(Grouped Weighted t-SNE，GW t-SNE)改进算法，该算法首先计算奇异样本在高维空间内的欧式距离，然后根据数据在高维中距离的不同远近关系进行分组，不同的分组采用不同的加权系数，使距离近的更近，远的更远，不近不远的保持不变.根据上述加权策略后，得到新的高维相似度距离度量方法并计算高维联合概率，再计算其低维联合概率，通过梯度下降的方法得到最小化的KL散度，并将其映射在二维空间内.

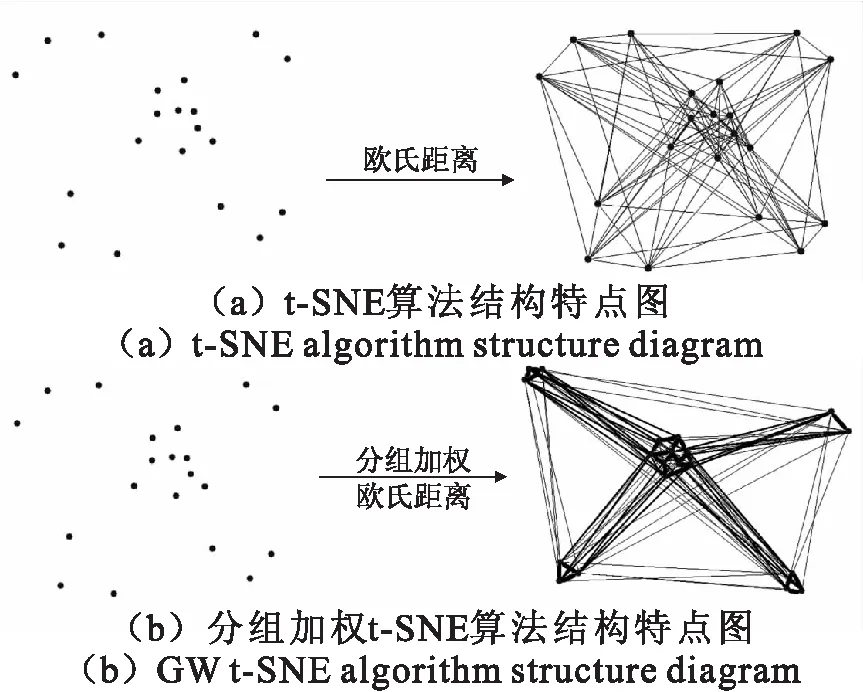
图2 Fig.2

该算法的原理如图2所示，其中图2(a)为t-SNE的相似度计算方法，无论样本之间相似程度多高，都是采用相同的欧式距离度量方法，该原理并不能反映出高维空间中样本分布的远近特征和相似关系的不同.而采用分组加权t-SNE算法的原理图见图2(b)，由于对不同的欧式距离样本对采用了不同的加权处理，使得在高维空间内距离较近的样本对的相似程度变得更高，距离较远的样本对的相似程度变得更低，而不近不远距离内的样本对相似程度保持不变，这使得其特征更加分明.

2.2 分组加权t-SNE降维算法的实现过程

本文算法首先计算出xi、xj在高维空间中的欧氏距离d(xi，xj)，并对这个欧式距离进行归一化处理，根据其距离分布特征进行分组，按照不同的距离特征进行合适的权重选取，进行加权，从而得到加权欧氏距离 d*(xi，xj).在使用分组加权t-SNE算法降维时，将加权欧氏距离替换欧氏距离，计算xi、xj在高维空间中的联合概率pij；得到yi、yj的低维空间联合概率qij；并用KL散度构建目标函数，通过梯度下降法求取数字手写体的低维表达最优解.

传统的欧氏距离计算表达式为：

(1)

在加权t-SNE算法中，通过高维目标函数的输入，可以得到其高斯核函数d(xi，xj)，它为两特征向量数据xi和xj之间的距离，即为欧氏距离.想进行加权，则先对高维样本空间的欧氏距离做归一化处理，得到矩阵m：

(2)

当dij=dmin时，m取最小值为0；当dij=dmax时，m取最大值为1.由式(1) 可以知道，加权的欧氏距离可以表示为：

(3)

其中，α表示每个距离分类的权重.

本文目前研究中将距离分为三类，近距离，较近距离和远距离，并对其进行加权，使得近距离越近，远距离越远，中间距离不变，从而得到加权距离d*=α·d.此时样本高维相似性条件概率pi|j和pj|i变为：

(4)

其中，δi是以数字手写体数据点xi为中心的高斯函数的矢量方差.

高维联合概率pij为：

(5)

低维映射联合概率为qij：

(6)

该方法最终优化目标定义为：通过最小化高维样本相似度P和低维样本相似度Q之间的KL散度得到最优结果.梯度下降的求导如公式(7)、公式(8)所示：

(7)

(8)

分组加权t-SNE算法流程图见图3，先设置总迭代次数M，另当前迭代次数为m，输入N个1*784的手写体数字样本向量，按上文步骤完成映射并将结果输出到低维空间内.

分组加权t-SNE算法运用加权欧氏距离来计算样本之间的相似度，可以反映出不同样本在高维空间内分布的远近程度，对高维降维数据中更好地保留其重要特征能起到更好地效果，由此使得高维相似度高的同类数据距离更近，相似度低的不同类数据距离更远，可以使低维空间的映射结果更加如实地反应在高维空间内的相似程度.

图3 分组加权t-SNE算法的流程图Fig.3 Flow chart of GW t-SNE algorithm

3 实验及结果分析

3.1 手写体数字奇异样本库的构建

根据MNIST手写体库，选择n个特征特异难以识别的手写体数字图片组成实验样本库，每一个图片是28*28大小的bmp图片，将其转换为n*784的高维矩阵，并将这些灰度图进行二值化处理，最终形成由0和1构成的n*784的矩阵，这就是要进行降维的高维数据，具体过程如图4所示.

图4 手写体数字奇异样本库的构建方法Fig.4 Construction method of handwritten digital singular sample library

3.2 实验设计

首先，对选择的手写体样本使用t-SNE算法进行降维及可视化，图5为2500个奇异样本数据经过t-SNE算法进行降维并映射到二维坐标的降维结果，从图中可以看出相对于其它数字，由于数字4和数字9的外形相似，因此在映射过程中出现了较多的重合，数字3、5、8的分布也较为紧密，这给手写字数字的识别带来了困难，同时也是出现误判的主要原因.因此下文将分组加权t-SNE的手写体数字降维算法分别用于手写体数字4、9以及手写体3、5、8的降维和聚类，通过使用t-SNE和分组加权t-SNE算法后的降维效果来展开对比和分析.

图5 奇异手写体数字0-9进行t-SNE算法降维结果Fig.5 Singular handwritten numeral 0-9 performs t-SNE dimensionality reduction results

3.2.1 降维及可视化实验

首先选择手写体数字4和9为一组，为了更深入的对比结果，根据样本数的不同，分别构建了奇异样本数为2000个和4000个的两个样本集.对两个样本集里不同的手写体数字奇异样本4和9分别使用t-SNE算法进行降维，再使用本文的分组加权t-SNE算法进行降维，并实现二维空间内的可视化，通过二维可视化图从聚类结果上进行对比分析.

接着在MNIST手写体库中选择易混淆的奇异手写体样本3、5、8为实验数据，同样构建2000个和4000个的不同样本集进行降维可视化映射.分别使用t-SNE算法和本文的分组加权t-SNE算法进行降维和可视化聚类.

需要说明的是由于t-SNE降维算法是将每个点通过梯度下降法进行低维映射，因为在这个过程中有随机量，所以每一次的降维结果分布会有不同，其二维坐标没有真实意义，只是用于代表映射后这些样本的相似程度.

3.2.2 实验结果的评价指标

除了可视化结果对比之外，本文还将通过查全率和查准率[22]两个评价指标对实验结果进行评价.

表1 分类结果混淆矩阵Table1 Confusion matrix of classification results

查准率P=发现的正确的映射个数/发现的所有映射个数，见公式(9)：

(9)

查全率R=发现的正确的映射个数/存在的映射数，如公式(10)：

(10)

为了能准确的对比其降维效果，选择相同的数据样本集，分别使用t-SNE算法和本文给出的分组加权t-SNE算法对其进行降维处理，使用相同的方法分别计算它的查全率和查准率.指标计算思想如下：首先分别计算出每个数字进行t-SNE降维后映射在二维空间上坐标的中心坐标，并以其中心坐标为圆心规定相同半径进行画圆，在此圆范围内，计算其评价指标.其次计算同一数据样本进行加权t-SNE算法降维，再用同样的方法计算映射后二维空间上的中心坐标，保持同组样本中相同数字的半径与t-SNE算法相同，并计算改进后算法的评价指标.

图6 数字手写体分组加权t-SNE降维算法实验过程图Fig.6 Digital handwritten GW t-SNE dimension reduction algorithm experimental process chart

由于查全率和查准率是一对矛盾的度量，一般来说，查全率越高查准率越低，查准率越高查全率越低.因此在进行实验结果验证时，要综合分析两个指标以确定降维方法的效果.需要说明的是在使用非线性降维的方法衡量样本的聚类效果时，由于样本映射到二维的点分布并不是固定的，分布也是不均匀的，计算查全率和查准率时并非直接固定其点的坐标，而是固定其相同的面积，因此在查全率和查准率上达不到均为90%的效果.此外由于本文的实验数据是奇异样本库，因此与使用机器学习算法对标准手写体数字样本库所得到的查全率与查准率的指标结果有所区别.图6为数字手写体分组加权t-SNE降维算法实验过程图.

3.3 实验结果对比及分析

3.3.1 可视化的对比及分析

图7是相同数字4、9在不同数据样本中分别进行t-SNE和分组加权t-SNE算法中的降维可视化图.

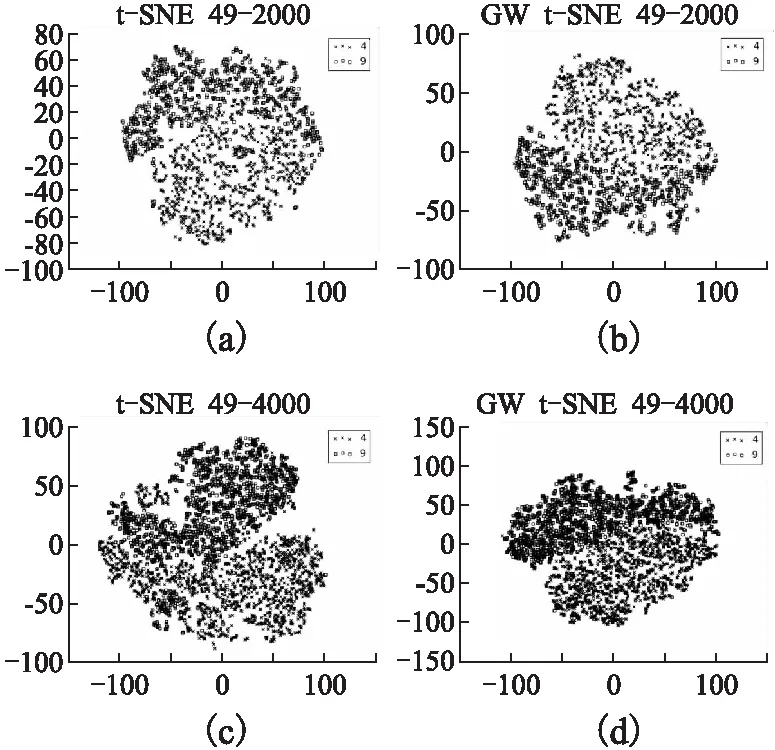
图7 数字4、9进行t-SNE和分组加权t-SNE算法的降维可视化结果Fig.7 Dimensionality reduction visualization results of t-SNE and GW t-SNE algorithm are carried out in figures 4 and 9

图7(a)为2000个4、9数据样本集在t-SNE算法中的降维效果，通过图可以清晰地看到，相同数字映射点之间间距大，图7(b)经过分组加权t-SNE算法降维后，发现相同数据点之间联系更加紧密，而不同数据点之间相对分散.

图7(c)是4000个数据样本集在t-SNE算法中的降维效果，数字4、9在可视化图中有交叉，说明数字4、9在此方法下无法清晰地分为两类.但在图7(d)的分组加权t-SNE算法可视化图中，手写体4、9虽仍有交叉部分，但可以清晰地分为两类，在二维可视化图中本文算法明显优于t-SNE算法.

图8是数字3、5、8在不同数据样本中分别进行t-SNE和分组加权t-SNE算法中的降维可视化图.

图8 数字3、5、8进行t-SNE和分组加权t-SNE算法的降维可视化结果Fig.8 Dimensionality reduction visualization results of t-SNE and GW t-SNE algorithm are carried out for numbers 3，5 and 8

图8(a)为2000个3、5、8数据样本集在t-SNE算法中的降维效果，通过图可以清晰地看出，数字之间有明显的交叉，且各个点分布稀疏.图8(b)经过分组加权t-SNE算法降维后，发现相同数据点之间联系十分紧密，且没有被其它数字完全阻隔的现象.

图8(c)是4000个数据样本集在t-SNE算法中的降维效果，数字3、5、8在可视化图中相同数字分布没有很紧密，交叉和聚类错误的点较多.但在图8(d)的分组加权t-SNE算法可视化图中，手写体3、5、8相同部分联系明显更紧密，且没有过多的交叉和重叠，因此在降维后二维可视化的聚类结果对比中，可以得出本文算法优于t-SNE算法.

3.3.2 评价指标对比及分析

图9是本文中选取的2000个样本中每个数字的评价指标的对比，图9中(a)、(c)为查全率的对比，(b)、(d)为查准率的对比，图(a)、(b)为2000个奇异样本数据集，图(c)、(d)为4000个奇异样本数据集.其中左侧表示t-SNE算法计算出的评价指标，右侧表示本文算法加权t-SNE计算出的评价指标.

从柱状图9中，明显可以看出分组加权t-SNE算法在查全率和查准率中，比t-SNE算法均有提高.

通过以上几组数据对比可以发现，二维图中同类各点分布明显聚拢，分界线相对明显，评价指标的查全率和查准率也有所提高.由于t-SNE算法存在随机变量，无法消除每次降维结果在二维空间内的随机映射现象，因此采取多次计算求平均值的方法，对查全率和查准率进行评价，评价结果表明，同组数据多次进行t-SNE和加权t-SNE算法计算后，每组查全率平均有了4%的提高，同时查准率平均也有了3.3%的提高.由于查全率和查准率是互相矛盾的一对变量，但在本文实验中，两个数字的评价指标同时都得到了提高，说明了分组加权t-SNE算法比t-SNE算法的性能更好，因而可以更好的保留数字手写体在高维的主要特征.

图9 4.9.3.5.8在t-SNE和分组加权t-SNE算法中的评价指标的对比Fig.9 Comparison of the evaluation indexes of 4.9.3.5.8 in t-SNE and GW t-SNE algorithms

4 结束语

本文以提高数字手写体易混淆奇异样本的识别率问题为目标，提出了一种分组加权t-SNE的手写数字奇异类样本聚类方法，通过对高维空间中不同欧式距离的样本对采用不同的分组加权算法计算距离，再根据新的评价距离计算高维空间中各数据样本对之间的联合密度和条件相似度的方法，达到了使高维空间内样本相似度估计更加精确的效果，从而提高了手写体数字库中奇异样本和易混淆样本的识别度.

实验结果显示，在低维聚类可视化结果图中，同类的明显结合更紧密，不同类区分更明显.并且使用分组加权的t-SNE算法在奇异手写体数字样本的查全率和查准率上均得到了提升.多次实验结果统计显示，加权t-SNE算法的查全率比t-SNE算法查全率平均提高了4%，查准率平均提高了3.3%.由此可见，本文方法对数字手写体中奇异样本在高维中主要特征的保留比普通t-SNE算法要好，因此可以得到更准确的降维效果并提高识别度，从而为手写体数字的奇异样本研究提供了理论和技术基础.

尽管本文所述方法对奇异手写体聚类有一定的改善效果，但是使用该方法将高维空间中的样本映射到低维空间中的效果还有很大的提高空间，并且该方法中高维距离分组和权重的选择对降维结果也都有一定的影响，下一步的工作也将针对这些因素展开深入研究和优化.