航空铆钉连接件的抗冲击性能

汪存显，高豪迈,，龚煦，索涛,3,*，李玉龙,3，汤忠斌,3，薛璞,3，侯亮，林家坚

1. 西北工业大学 航空学院，西安 710072 2. 中国航发商用航空发动机有限责任公司，上海 200241 3. 陕西省冲击动力学及工程应用重点实验室，西安 710072

铆接是一种无法拆卸的永久性连接，由于其拥有工艺过程简单、价格低廉、连接强度稳定可靠等诸多突出优势，因而成为航空领域应用最为广泛的连接方式[1]。通常，一架大型飞机完成整机装配所需要用到的铆钉和螺栓的数量往往可以达到150万到200万之巨[2]。飞机上铆钉连接结构的强度往往对飞机的整体结构强度有着显著的影响。尤其在飞机结构承受诸如飞鸟等离散源撞击时，极有可能造成铆接结构的失效，影响飞机的飞行安全[3]。

国内外的大多数学者将精力主要集中在铆接结构的疲劳寿命预测和静强度校核上[4-10]，然而，正如金属材料往往表现出应变率效应一样，单纯的准静态力学试验通常并不能准确地描述铆接结构在动态载荷作用下的力学行为。因此，开展铆接结构动态力学性能试验和数值模拟具有一定的必要性和迫切性。

截止到目前，在铆钉材料及其结构的动态力学性能的研究中，国内外的一些专家和学者已经开展了部分工作，并取得了一定的成果。在试验方面，Li等[11]在准静态和名义加载速度为4 m/s和8 m/s的情况下，对飞行器应用中常见的7种连接结构进行了拉伸试验。结果显示，所测试的7种铆钉连接结构中，加载速率对于铆钉连接结构的拉伸强度的影响不大，但铆钉连接结构所吸收的平均总能量随加载速率的增加而增加；对于不同的铆钉连接结构，其破坏模式也不尽相同，即使是相同的铆钉连接结构，其破坏模式也会随着加载速度的不同而发生变化。Wood等[12]使用了高速液压伺服试验机研究了自冲铆钉连接的铝板(A5754)在典型的汽车碰撞速度下的力学性能，并进行了数值仿真研究。刘小川等[13]在液压伺服试验机上进行了准静态至10 m/s的拉伸与剪切实验，并将速率项引入了工程失效准则。Porcaro等[14]利用霍普金森压杆装置进行了动态载荷作用下自冲铆钉连接结构的拉伸和剪切试验，提高了动态情况的加载速率，同时利用LS-Dyna有限元软件进行仿真模拟，并与试验结果进行比较；结果表明，自冲铆钉的破坏形式与加载速率之间并不存在明显的相关性。然而，在这些研究中，人们只对铆接结构进行了简单的动态纯拉伸、纯剪切试验，而对其动态的拉剪耦合试验还鲜有涉猎；此外，对于较高加载速率下的试验，所使用的试验装置采用了Hopkinson压杆系统，导致了试验中往往需要设计非常复杂的夹具，且使用了尼龙材质的大直径(60 mm)入射杆和透射杆，导致严重的应力波弥散效应，影响了试验的准确性。

在有限元数值模拟方面，Langrand等[15-18]通过数值建模和试验测量研究了应变率对铆接结构失效的影响。其中数值建模采用了Gurson细观损伤力学模型实现铆钉的模拟，结果表明，发明一种新型的考虑材料非线性的铆钉单元是非常必要的。Sun等[19-20]在Gurson模型的基础上考虑了孔洞形状的影响，采用了Gologanu模型并将其与3种失效准则相结合，描述了连接强度随着材料中孔洞演化而产生的变化。Hanssen等[21]则通过引入自定义的损伤参量，成功地用简化的铆钉模型模拟了不同加载角度下铆接结构的力学行为和损伤演化过程。模拟了自刺铆钉连接的不同金属板的残余应力分布，并与实验测量结果进行了比较。Huang等[22]模拟了铆钉连接的不同金属板的残余应力分布，并与实验测量结果进行了比较。张旭[23]基于LS-Dyna有限元分析软件，建立了电磁铆接过程电磁场-力场-温度场耦合数值模拟模型。其模型在Johnson-Cook模型的基础上，实时考虑了电磁场、力场以及温度场之间相互影响，对整个电磁铆接过程进行了系统分析。然而，关于铆钉连接结构的建模方法均较为复杂，且仍存在不完善的部分，尚未有研究能够提出一种令人广泛接受的方法。

本文设计了基于分离式Hopkinson拉杆系统的铆接结构动态力学性能测试装置，对以MS20615铆钉和TC4钛合金铆接试验件构成的铆接结构进行了动态下的纯剪切、30°拉剪耦合、45°拉剪耦合、60°拉剪耦合和纯拉伸试验，得到了该铆接结构的动态力学性能。同时利用电子万能试验机对该铆接结构进行了2种加载速率下的准静态纯剪切、30°拉剪耦合、45°拉剪耦合、60°拉剪耦合和纯拉伸试验，并将该试验结果和动态试验结果进行对比，讨论了加载角度、加载速率对铆接结构力学性能的影响。基于所测得的材料本构及失效参数，利用商业有限元软件LS-Dyna对铆钉的压铆过程和铆接结构的动态试验过程进行数值模拟，讨论了压铆过程产生的残余应力场对铆接结构力学性能的影响。本文的研究结果对于航空铆钉连接件在工程中应用、尤其是抗冲击领域的应用具有指导意义。

1 试样准备与试验过程

1.1 试样准备

铆钉结构所采用铆钉为Monel400镍铜合金半圆头铆钉，牌号MS20165。铆钉的钉杆直径为5/32英寸，约为4.0 mm，铆钉的有效长度为5/16英寸，约为8.0 mm。铆接试验件材料为TC4钛合金。铆钉和铆接试验件材料的基本力学性能参数如表1所示。

铆接结构试验主要包括准静态和动态下的纯剪切、30°拉剪耦合、45°拉剪耦合、60°拉剪耦合和纯拉伸试验。铆接试验件设计尽可能满足分离式Hopkinson拉杆系统的要求，为了与工程实际一致，铆接试验件平板部分的厚度分别为1 mm和1.1 mm。图1给出了不同铆接试验件与分离式Hopkinson拉杆系统连接方式。图2(a)给出了铆接结构加载角度定义。其中，θ为铆接结构的加载角度，FN与FS分别为铆接结构失效载荷F的法向分量与切向分量。对于铆接结构纯剪切试验，由于载荷相对较小，主要采用胶接方式，而对于拉剪耦合和纯拉伸试验，其载荷相对较大，前者采用胶接和销钉固定共同作用的连接方式，后者则直接采用螺纹连接的方式，以避免铆接结构试样与加载装置连接处在加载过程中发生脱落。

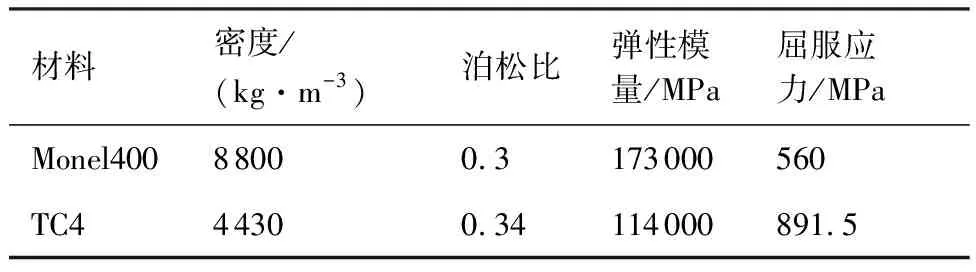
表1 Monel400镍铜合金及TC4钛合金材料参数

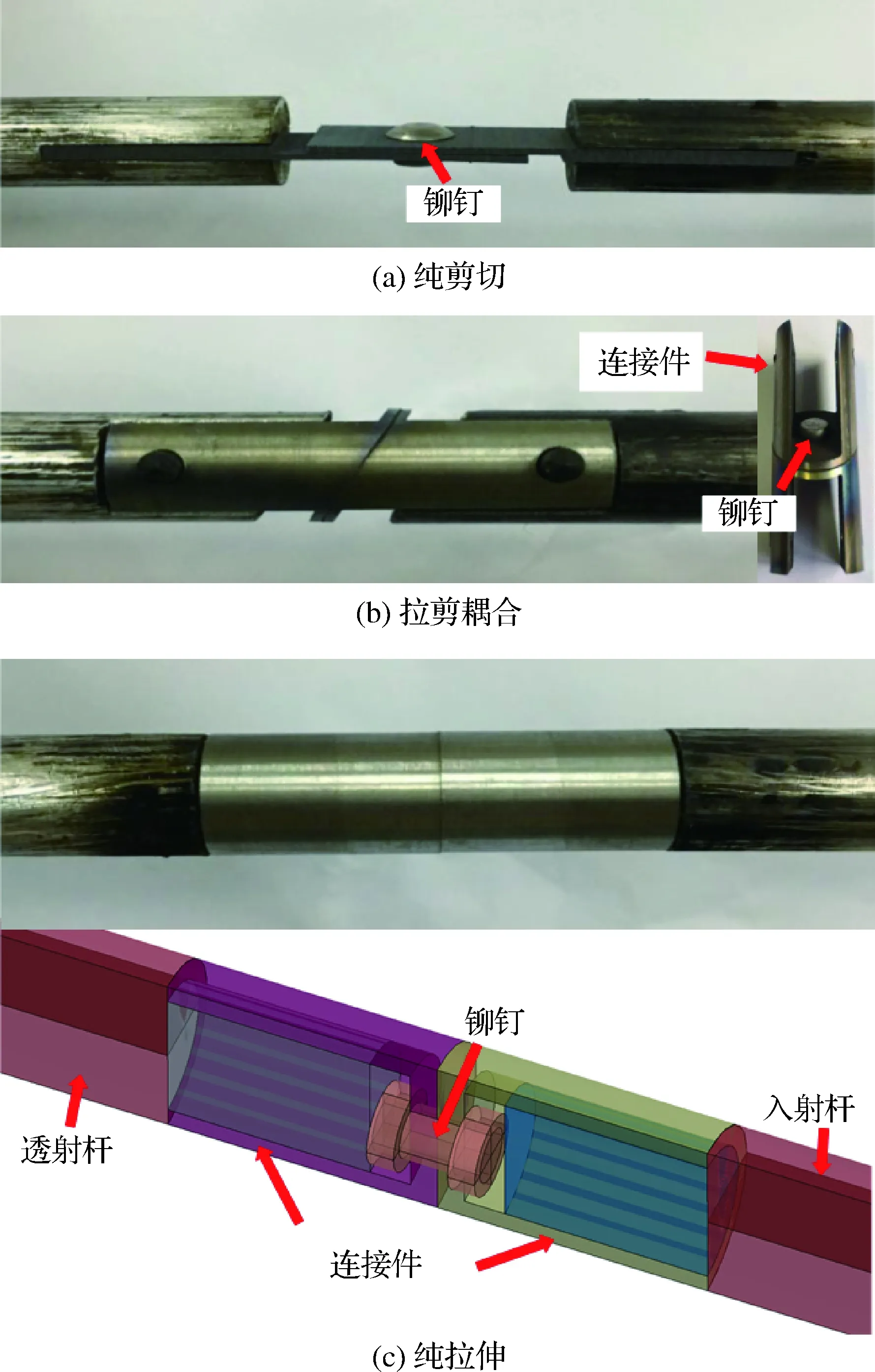
图1 铆接结构及其连接Fig.1 Riveting structures and their connection modes

试验前，需对铆接试验件进行铆接，在符合航空制造工程手册[24]的标准范围内，将铆钉镦头的外形制定为平圆台。铆钉直径为d，铆钉墩头最大直径为D，铆钉墩头最小直径为D′，则

D=1.5d

(1)

D′=d+a

(2)

其中，a取0.4 mm。铆钉镦头高度h则按照铆钉直径大小来确定，如图2(b)所示。考虑试验的一致性，本文中的铆接过程统一使用气动压铆机来完成，从而确保铆接结构制备的统一性。

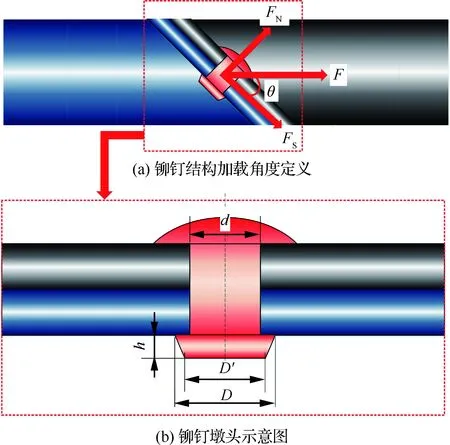
图2 铆钉结构加载角度定义及铆钉墩头示意图Fig.2 Loading angle definition of riveting structure and diagram of rivet upset head

1.2 试验装置与原理

1.2.1 准静态实验

铆接结构的准静态试验采用CSS-88010电子万能试验机进行，在试验过程中，采用引伸计测量铆接结构的变形，并结合载荷传感器所测得的铆接结构所受载荷，最终得到其载荷-位移关系曲线P-ΔL。

1.2.2 动态实验

铆接结构的动态试验采用分离式Hopkinson拉杆装置进行。如图3所示，分离式Hopkinson拉杆装置由气室、撞击杆、入射杆、透射杆、信号采集系统和夹持系统共同构成。拉杆装置的撞击杆是一个环形长管，入射杆距离试件较远的一端为一种带凸台的结构，撞击杆在气室中高压气体的作用下以一定的初速度撞击入射杆凸台，在凸台中产生一个压缩方向的应力波，该应力波在自由端面反射后，在入射杆中生成一个拉伸方向的应力波向试样传播，从而实现对试样施加动态拉伸载荷。由于试样与杆的波阻抗不匹配，一部分入射波在端面通过反射回到入射杆中，另一部分经过试样传播到透射杆中，采用粘贴在杆上的应变片可以测量入射杆和透射杆上的脉冲信号。

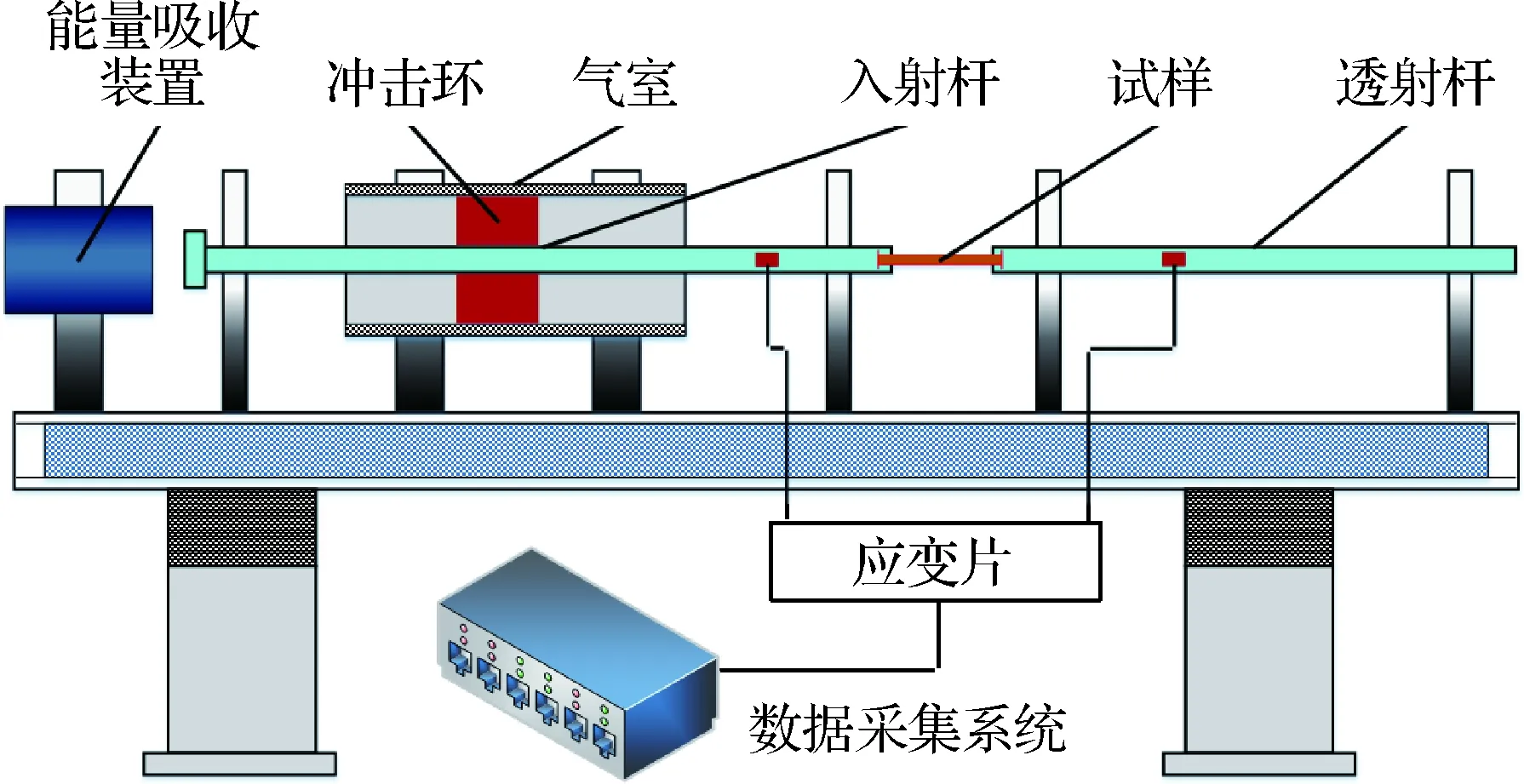
图3 Hopkinson拉杆装置示意图Fig.3 Diagram of split Hopkinson tension bar

由于沿Hopkinson杆轴向方向传播的应力波的幅值以及杆上的质点速度都可以通过应变片精确测得。根据一维弹性波理论[25]，这些参数在Hopkinson杆上任意点处的数值均相等。因此，可以根据入射杆和透射杆上应变片所测得的信号分别得到铆接结构在入射端面和透射端面上的载荷和质点运动速度的信息，用于描述铆接结构的动态力学行为，如式(3)～式(6)所示。

FInput(t)=SbE(εI(t)+εR(t))

(3)

FOutput(t)=SbEεT(t)

(4)

VInput(t)=C0(εI(t)-εR(t))

(5)

VOutput(t)=C0εT(t)

(6)

式中:FInput、FOutput、VInput和VOutput分别为铆接结构表面的载荷和速率；Sb、E和C0分别为Hopkinson杆的横截面积、弹性模量和弹性波波速；εI(t)、εR(t)和εT(t)分别为入射波、反射波和透射波脉冲；t为时间。对于铆接结构，无法用传统的应力应变曲线去描述铆接结构的动态变形特性，因此，试验中选取载荷P(t)和位移ΔL(t)来描述铆接结构的动态变形特性。在变形均匀的假设下，利用这些载荷和质点速度信息即可进一步获得铆接结构的载荷与位移信息，其与试验测量参数的关系为

P(t)=FOutput(t)

(7)

(8)

式中:τ为时间t在积分式中的变量表示。

2 试验结果

2.1 准静态试验结果

为了给铆接结构的动态试验结果提供一个准静态力学性能的参照对比，在进行铆接结构的动态试验前，首先对铆接结构开展了加载速率v为5×10-6m/s和5×10-5m/s的准静态试验。纯剪切、45°拉剪耦合和纯拉伸加载情况下铆接结构的准静态载荷-位移曲线如图4所示。

2.2 动态试验结果

在利用分离式Hopkinson拉杆装置对铆接结构进行动态加载试验时，采用调节气压的方式控制子弹撞击入射杆自由端凸台的速度，从而达到控制铆接结构动态加载速率的目的。由于铆接结构试样并非标准试样，应变率并不适合用于表征铆接结构试样的加载速率。因此，试验中利用铆接结构入射杆端面测得的速率VInput来表征动态试验的加载速率。图5给出了铆接结构在动态加载条件下的典型加载速率曲线。从图中可以发现，铆接结构的加载速率在动态加载过程中基本左右保持恒定，实现了较好的恒速率加载。

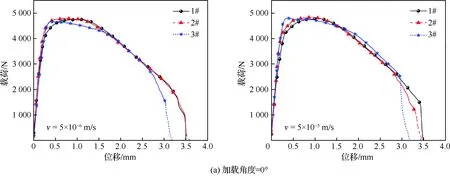
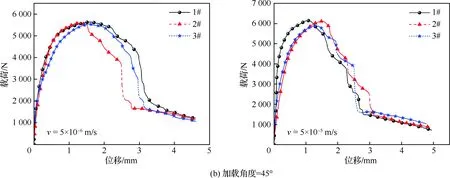
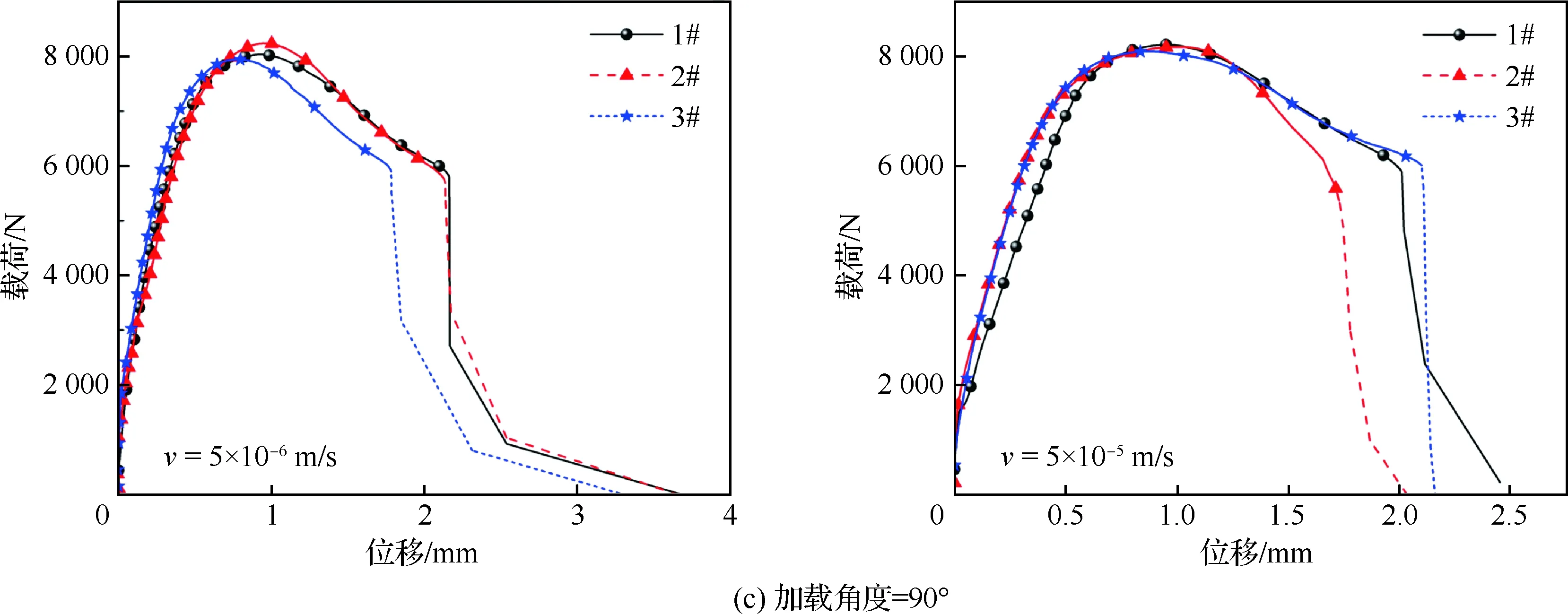
图4 准静态加载条件下铆接结构载荷-位移曲线Fig.4 Force-displacement curves of riveting structure under quasi-static loading condition

图5 铆接结构在动态加载条件下的典型加载速率曲线Fig.5 Typical loading rate curves of riveting structure under dynamic loading condition

由于铆接结构本身并非标准的拉伸试样，外形相对繁琐。当应力波传播至铆接结构时，波在其中的反射及透射机制较为复杂，极有可能出现应力不均匀的现象，从而影响试验结果的准确性与可靠性。在动态加载条件下，铆接结构试样在加载过程中是否达到载荷平衡是判断试验结果有效性的重要基准。图6给出了加载速率为15 m/s时，纯拉伸加载情况下铆接结构载荷-位移曲线对比和纯拉伸动态加载条件下铆接结构的一组典型α(t)-t曲线。结果显示，由入射杆和透射杆应变信号分别得到的铆接结构的载荷-位移曲线基本重合。载荷平衡系数由式(9)计算可得[26]

(9)

式中：FInput和FOutput分别为试样与入射杆和透射杆接触端面的载荷。由图可知，当时间达到52 μs时，载荷平衡系数降低至5%以下，铆接结构基本达到载荷平衡，此后载荷平衡系数虽有所起伏，但直到铆接结构试样失效，载荷平衡系数均低于5%，由此可以推断，该试验方法可以保证铆接结构在动态加载过程中达到载荷平衡，试验结果准确可信。

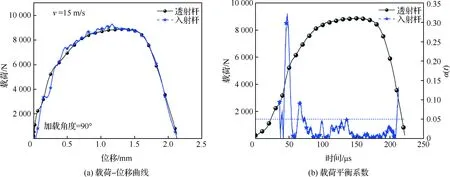
图6 纯拉伸动态加载情况下铆接结构载荷-位移曲线及载荷平衡系数Fig.6 Force-displacement curves and stress uniformity coefficient of riveting structure under dynamic pure tension loading condition

2.3 试验结果统计

铆接结构在动态纯剪切、45°拉剪耦合和纯拉伸加载情况下的典型载荷-位移曲线如图7所示。观察准静态及动态情况下铆接结构的载荷-位移曲线，可以发现曲线大致可分为弹性上升段、平台段、损伤下降段这3个部分。为了更好地说明铆接结构的力学性能，将铆接结构载荷-位移曲线达到最高点时的载荷定义为失效载荷，并将铆接结构失效瞬间的位移定义为失效位移，各加载情况下铆接结构的力学性能参数如表2所示。

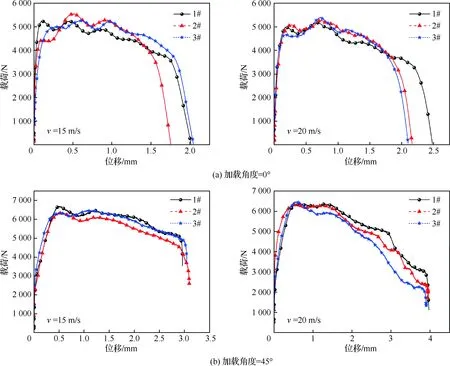
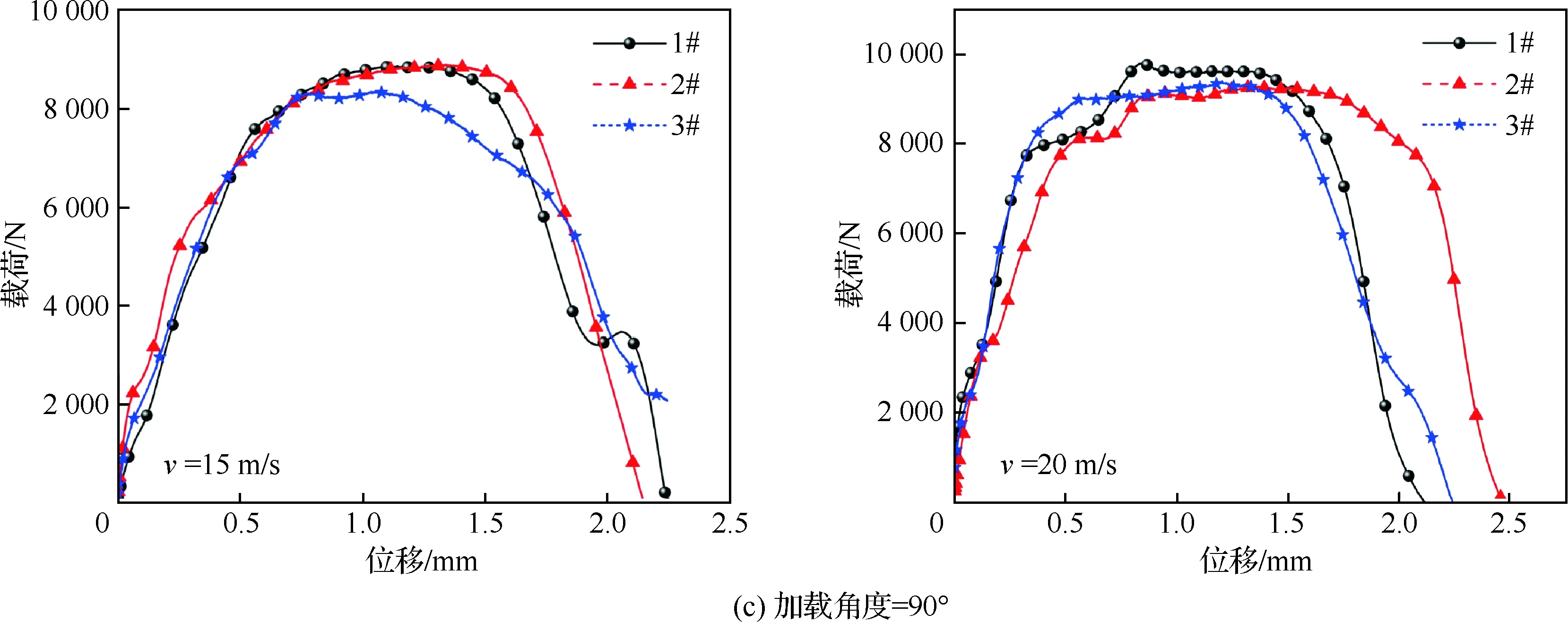
图7 动态加载条件下铆接结构载荷-位移曲线Fig.7 Force-displacement curves of riveting structure under dynamic loading condition

表2 铆接结构力学性能参数Table 2 Mechanical parameters of riveting structures

3 分析与讨论

3.1 加载角度的影响

铆接结构在不同加载角度下的失效模式图如图8所示。与此同时，图9给出了铆接结构在每种加载速率下，不同加载角度时的失效载荷和失效位移。结果显示，随着加载角度不断增加，即载荷从纯剪切向纯拉伸变化的过程中，铆接结构对应的承载能力有所提高，该铆接结构的抗拉伸能力要强于其抗剪切能力；铆接结构的失效位移则随着加载角度的增加大致呈现出先增加再减小的趋势，这是由于当加载角度为0°和30°时，铆接结构的受力主要表现为铆钉钉杆承受剪切载荷，从而造成铆接结构的失效模式为铆钉钉杆的脆性剪切断裂；而当加载角度增加到45°和60°时，由于载荷逐渐向拉伸方向转变，铆接结构受到的剪切载荷减小，拉伸载荷增大，此时铆接试验件的平板部分所受的载荷首先超过其承载能力，使得铆接结构的失效模式转变为铆接板部分的失效；当加载角度达到90°时，铆接结构承受纯拉伸载荷，由于铆钉钉杆的抗拉伸强度大于铆钉钉头的剪切强度，因而铆接结构的失效模式表现为铆钉钉头的断裂失效。

图8 铆接结构在不同加载角度下的失效模式Fig.8 Failure modes of riveting structures under different loading angles

由此可见，加载角度对铆接结构的失效模式有着重要影响，不同的加载角度会导致铆接结构产生不同的失效模式，而正是失效模式的改变引起了铆接结构位移规律变化。

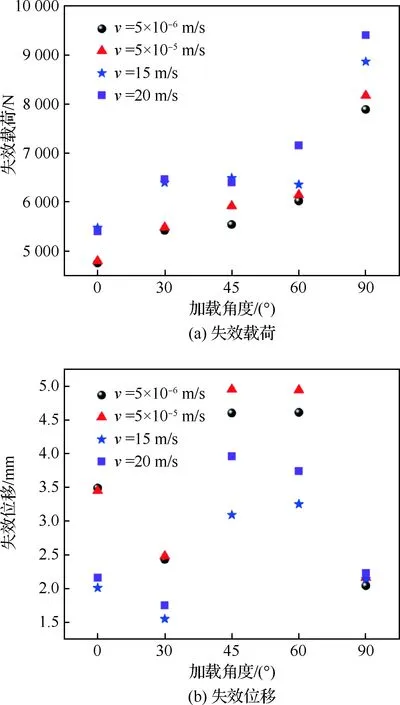
图9 铆接结构不同加载角度下的失效载荷和失效位移Fig.9 Failure loads and failure displacements of riveting structures under different loading angles

3.2 加载速率的影响

图10给出了铆接结构在5种加载角度下，不同加载速率时的失效载荷，并同样选取了加载角度30°时不同加载速率下铆接结构的载荷-位移曲线来进一步研究加载速率对失效载荷的影响。

结果显示，随着加载速率的增加，铆接结构的失效载荷整体上呈现逐渐增加的趋势，尤其当加载速率从准静态变为动态时，铆接结构的失效载荷明显增大。对于每一种加载角度，随着加载速率从准静态提高到动态，铆接结构的承载能力都得到了一定的提高。铆接结构的失效位移随着加载速率变化的规律并不十分明显。对于纯剪切、30°拉剪耦合、45°拉剪耦合和60°拉剪耦合试验，随着加载速率从准静态提高到动态，铆接结构的失效位移显著下降。而对于纯拉伸试验，铆接结构的失效位移随着加载速率的提高基本保持不变，这种特殊的现象可能是由该加载角度下铆接结构独特的失效模式导致的，即铆钉钉头的断裂失效所引起的结构失效位移几乎不受加载速率的影响。在相同的加载角度下，不同加载速率作用时，铆接结构的失效模式并不会发生变化，由此可以判断，当加载角度相同时，在一定加载速率范围内，加载速率对铆接结构的失效模式几乎没有影响；加载速率对失效位移存在一定的影响，但仍需考虑不同加载角度引起的不同失效模式。

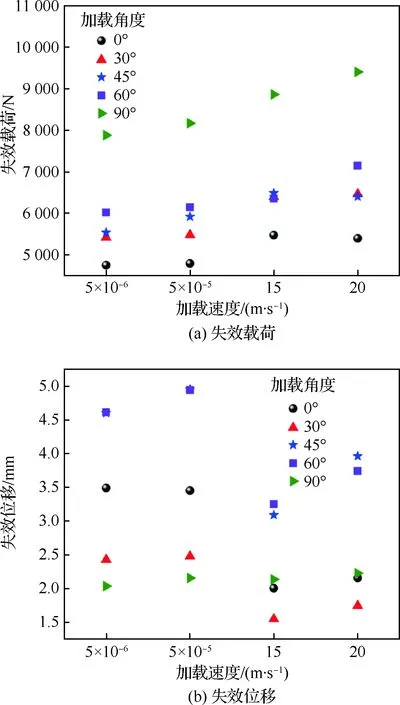
图10 铆接结构不同加载速率下的失效载荷和失效位移Fig.10 Failure loads and failure displacements of riveting structures under different loading speeds

3.3 铆接结构的失效面

如图2(a)所示，可将各加载情况下铆接结构的失效载荷分解为法向分量FN与切向分量FS，失效载荷F与法向分量FN与切向分量FS之间的关系可表示为

FN=F·sinθ

(10)

FS=F·cosθ

(11)

将铆接结构在纯拉伸、30°拉剪耦合、45°拉剪耦合、60°拉剪耦合、纯剪切等不同加载角度的加载情况下得到的失效载荷分解，以法向分量为横坐标，切向分量为纵坐标，可绘制得到铆接结构的失效面，如图11所示。

由图可知，随着加载速率从准静态到动态的提高，铆接结构的失效面呈现出逐渐往外扩大的趋势，这反映出铆接结构的承载能力会随着加载速率的提高而得到增强。由此可见，加载速率对铆接结构的失效有一定的影响，因而在建立铆接结构的模型时，考虑加载速率的影响是十分必要的。

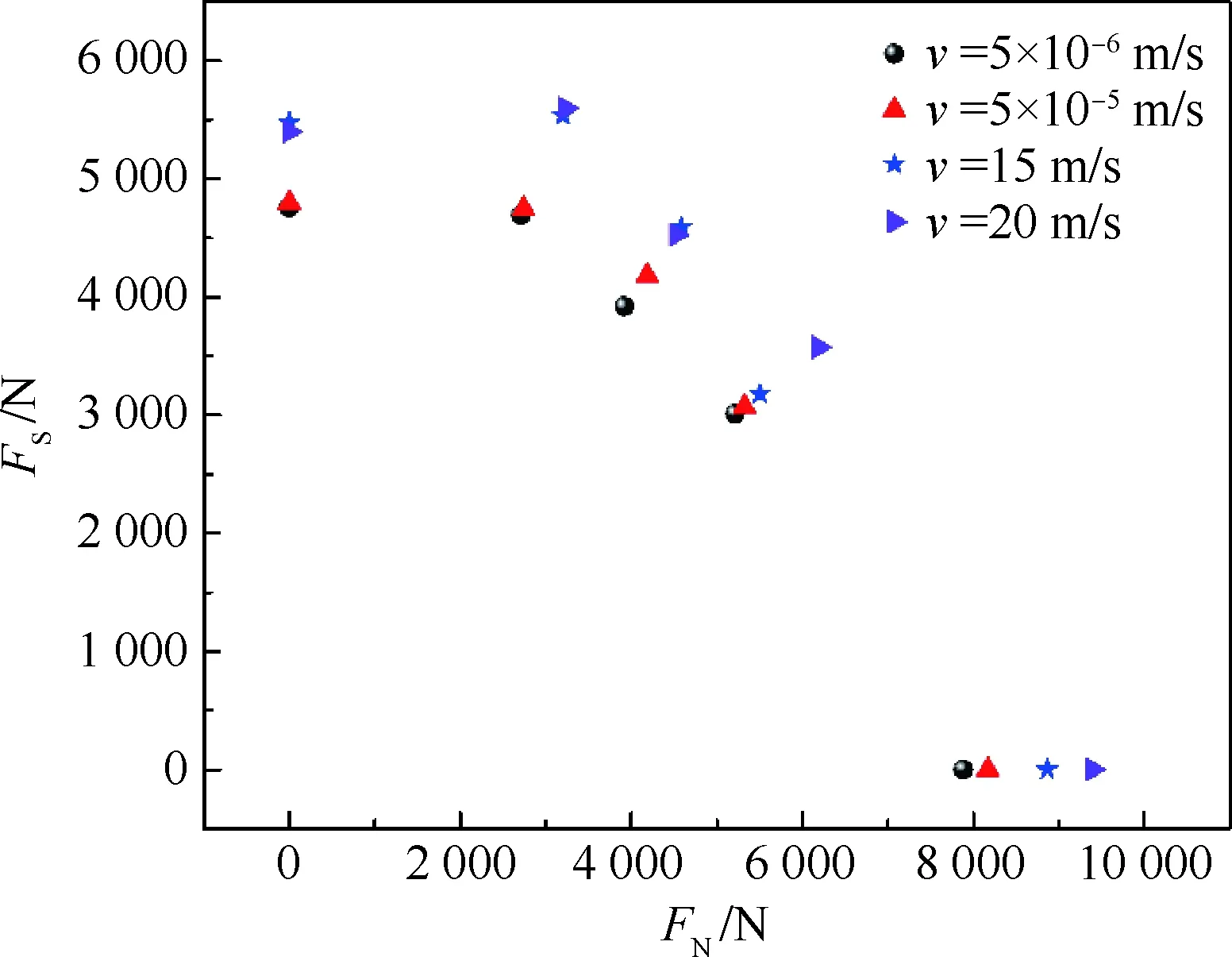
图11 铆接结构受力分解图和失效面Fig.11 Force decomposition and failure surfaces of riveting structures

4 铆接结构简化模型

4.1 动态试验过程数值模拟参数设置

由于飞机结构中的铆钉数量往往过于庞大，因此，在进行结构抗冲击仿真时，建立完整的细节模型往往需要耗费巨大的时间成本；同时，铆钉在尺寸上与结构尺寸相比存在着数量级上的差异，将铆钉及局部连接结构进行单元局部细化往往会带来十分冗长的计算时间。因此，在实际分析中，为了提高计算效率，在有限元仿真时需要对铆钉进行简化，并赋以一定的失效判据，以模拟铆接结构的失效。目前主流的商用有限元软件中常用的铆钉简化方式是建立铆钉单元来代替铆接结构，通过定义合理的失效判据并赋以准确的失效参数来模拟铆接结构的力学行为。

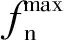
(12)

参数α为损伤参数修正项，其中α1和α2可对铆接结构在剥离与拉剪耦合加载情况下的受力进行修正，其对应的值通常小于1；α3的值通常要比1大，其主要作用是修正铆接结构在拉剪耦合加载情况下的失效位移；钉头直径d为铆钉的钉头直径，主要控制铆接结构的影响区域。根据第3节中铆接结构在准静态和动态条件下的试验结果，可得到*CONSTRAINED_SPR2模型的对应参数。表3给出了*CONSTRAINED_SPR2模型的各对应参数，用以支持铆接结构简化模型的数值模拟。其中，hm和hs分别为铆接结构主面及从面的厚度，ξn和ξt分别为铆接结构在纯拉伸和纯剪切加载条件下力位移曲线劣化的起始点。

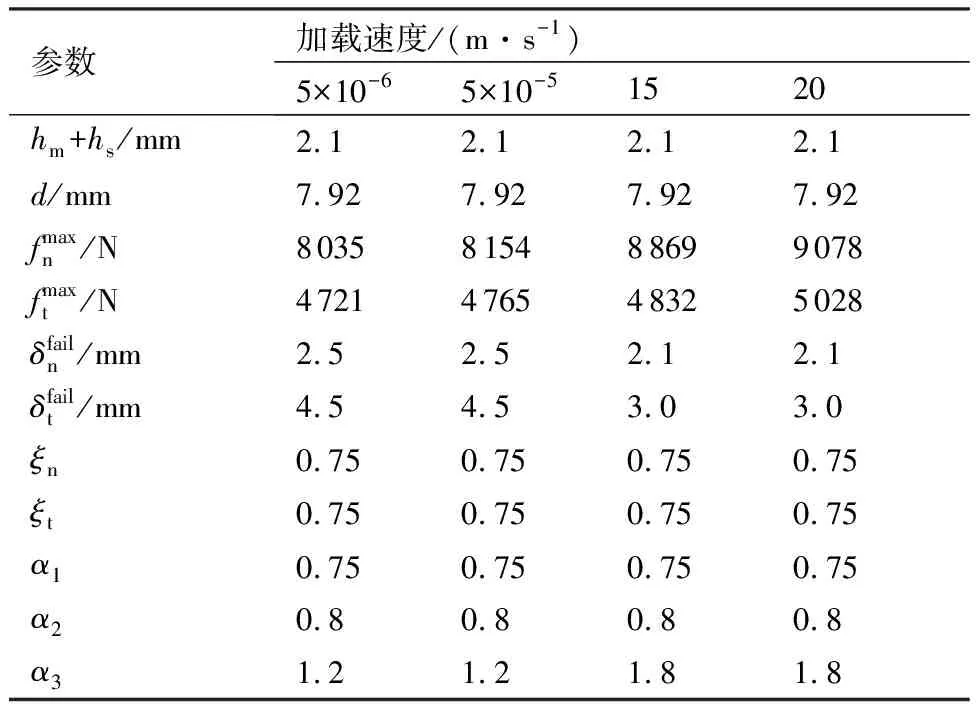
表3 *CONSTRAINED_SPR2参数表Table 3 *CONSTRAINED_SPR2 parameters

4.2 简化模型参数验证

为了验证*CONSTRAINED_SPR2模型的准确性，通过在LS-Dyna中建立壳单元简化模型对不同加载角度下的铆接结构动态纯拉伸、拉剪耦合及纯剪切试验进行数值模拟。简化模型采用Belytschko-Tsay壳单元(ELFORM=2)，并在壳单元厚度方向上设置3个积分点，网格尺寸大约为1 mm×1 mm；模型的接触采用automatic-surface-to-surface进行设置；在铆接结构的入射端设置了15 m/s的恒加载速率载荷实现动态加载。作为对比，选取加载速率为15 m/s时不同加载角度下的铆接结构动态试验结果验证简化模型的准确性。加载速率为15 m/s时不同加载角度下的铆接结构简化模型如图12所示。图13给出了采用*CONSTRAINED_SPR2的铆接结构简化模型的数值模拟结果与试验结果的对比。由图可知，铆接结构在纯剪切、45°拉剪耦合、60°拉剪耦合及纯拉伸加载情况下的仿真结果均与试验结果吻合较好，模型在失效载荷和失效位移上都能与试验结果得到较好的匹配。

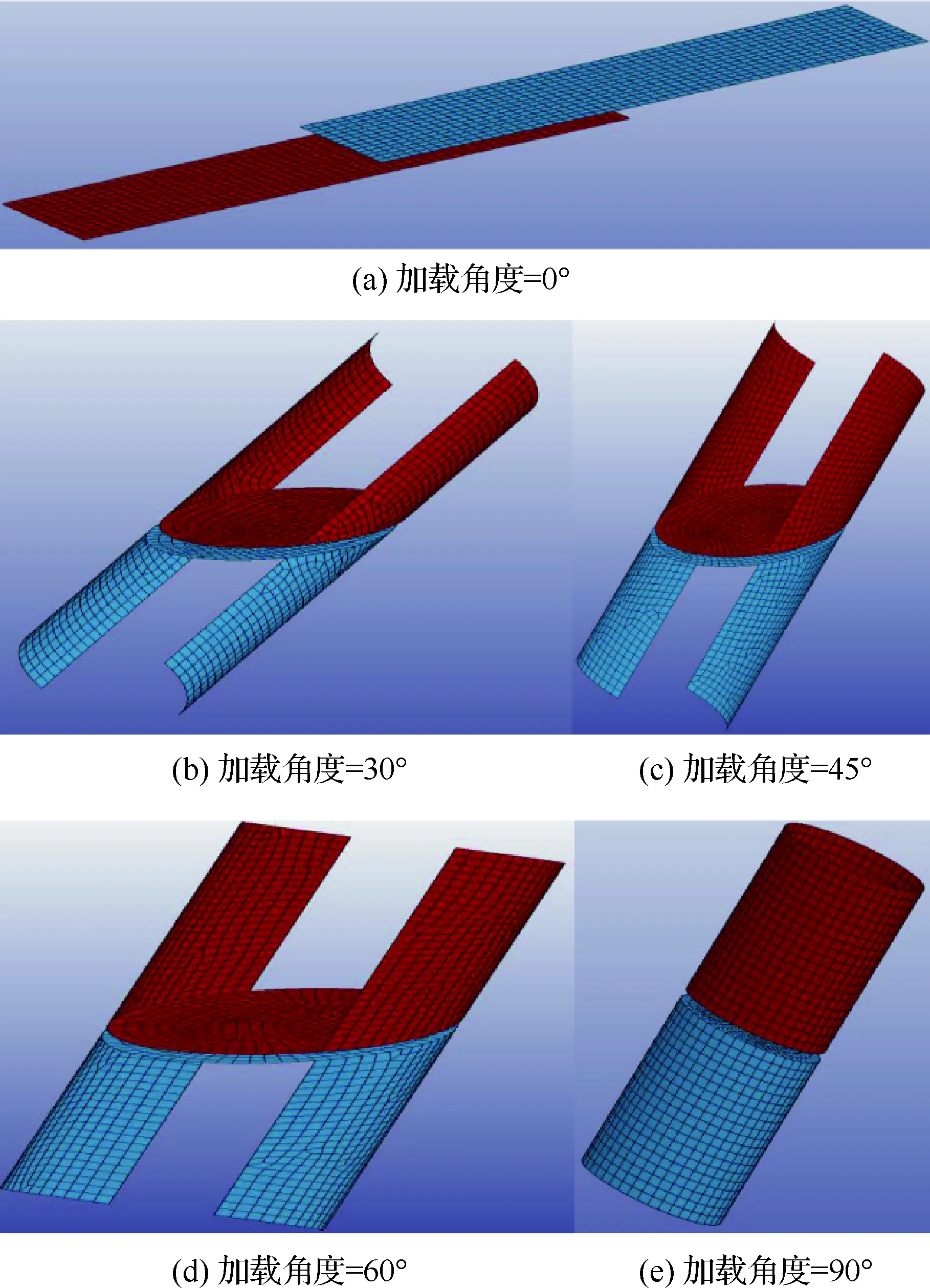
图12 动态铆接试验结构简化模型Fig.12 Simplified models for tests of dynamic riveting structure

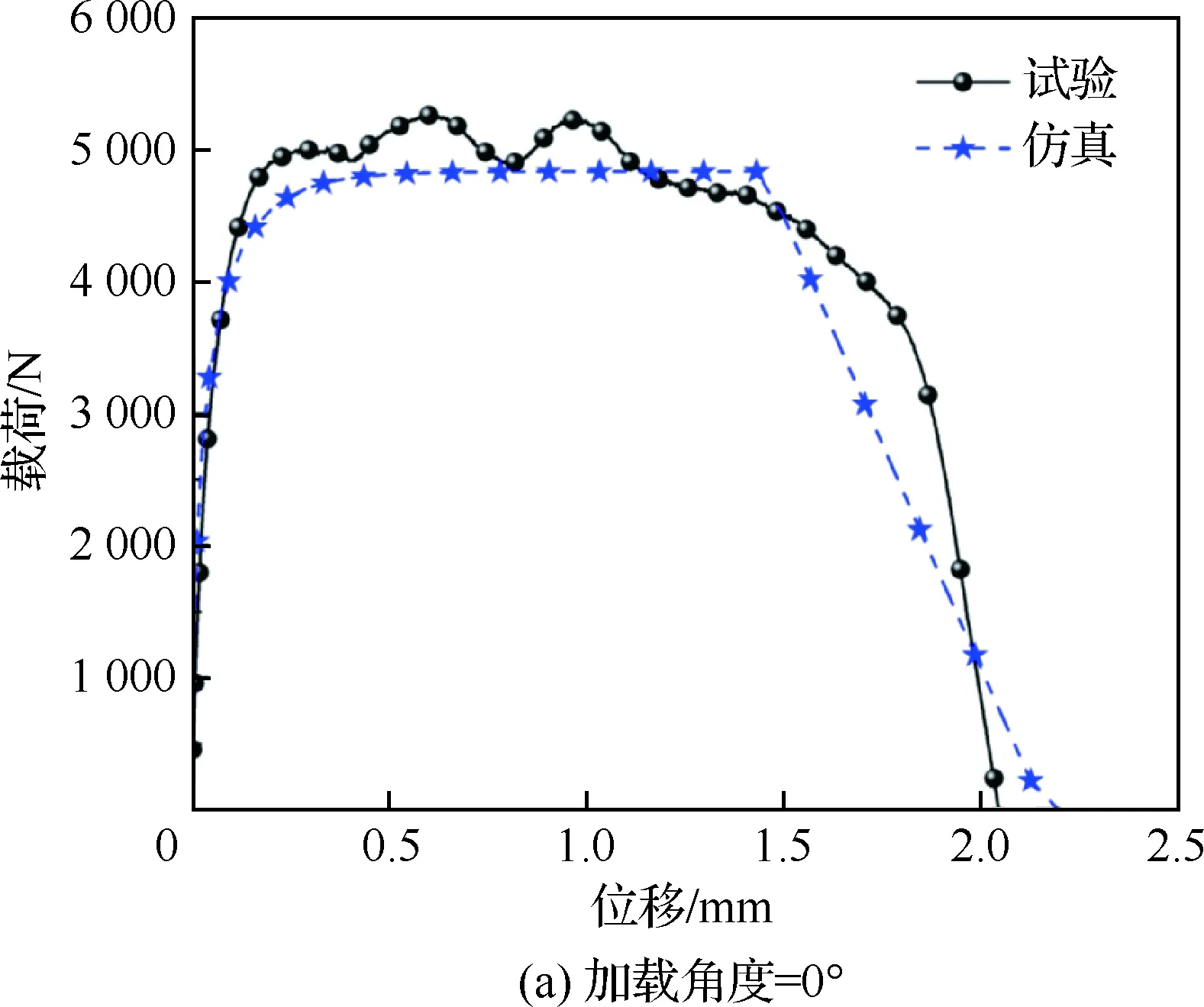
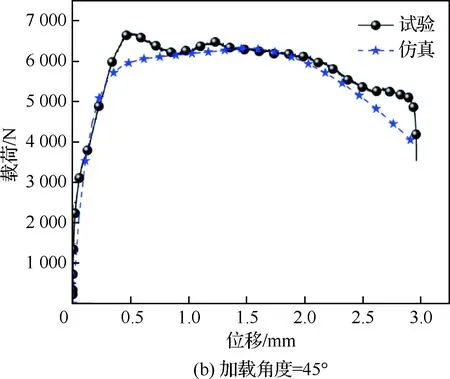
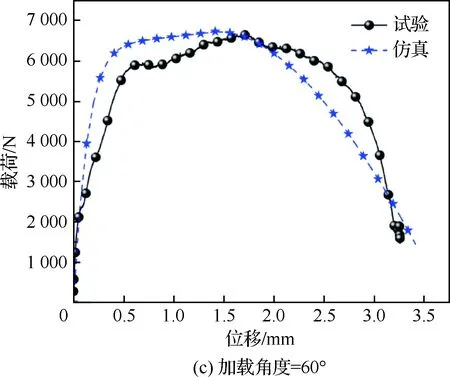
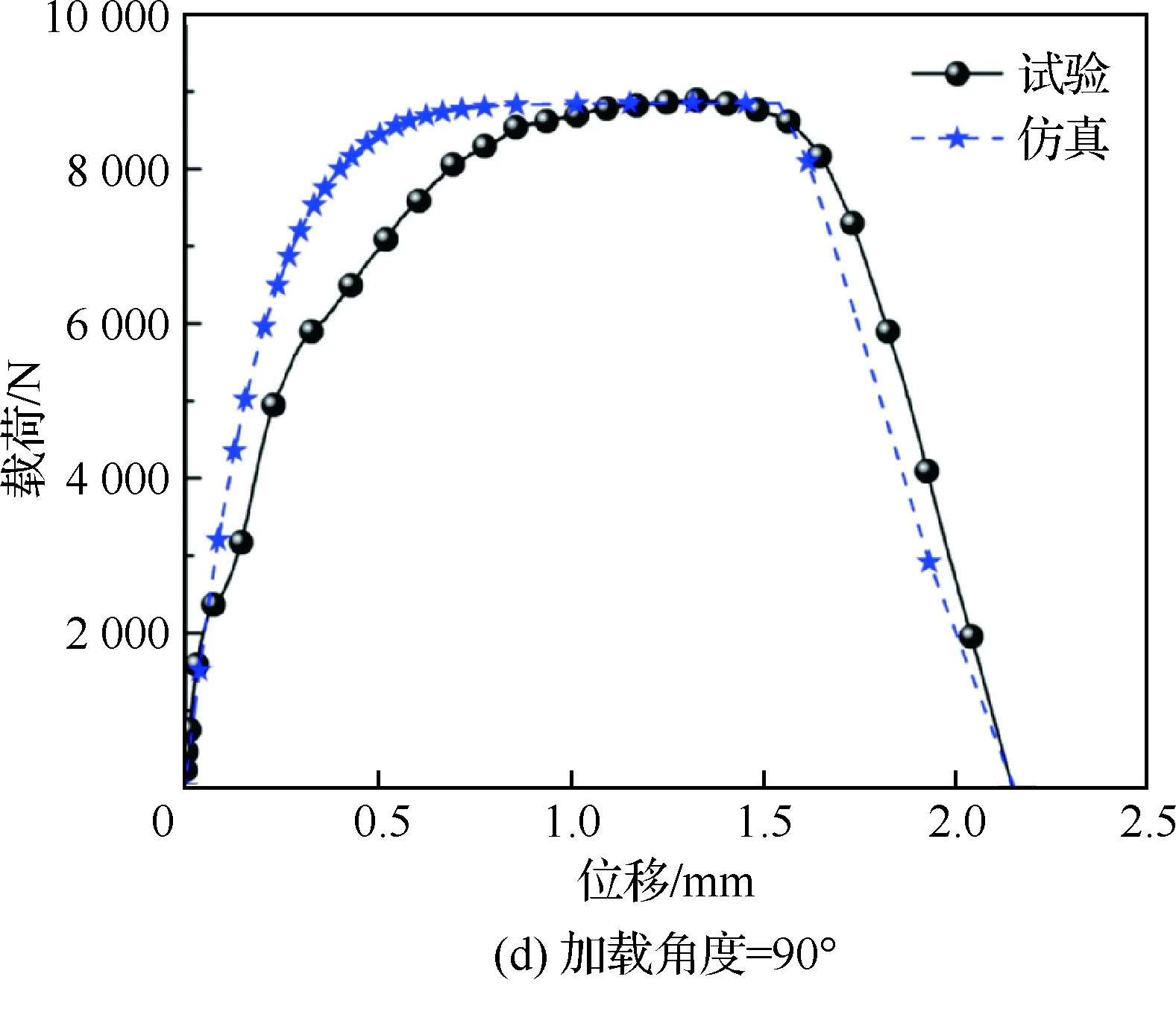
图13 铆接结构简化模型结果与试验结果对比Fig.13 Comparison between results of simplified models and test results

5 结 论

1) 设计了一种基于分离式Hopkinson拉杆系统的铆接结构动态力学性能测试装置，可以有效地实现铆接结构的动态纯剪切、拉剪耦合和纯拉伸试验。为铆接结构的动态力学行为研究提供了一种新的方法。

2) 当加载角度逐渐增大，即铆接结构所受载荷从纯剪切逐渐向纯拉伸变化的过程中，铆接结构的承载能力逐渐增大，该铆接结构承受拉伸载荷的能力强于其承受剪切载荷的能力。

3) 当加载速率逐渐增大，即铆接结构所受载荷从准静态变化为动态的过程中，铆接结构的承载能力显著增大，因而，加载速率对该铆接结构的承载能力有一定的影响，即该铆接结构的承载能力存在较为明显的加载速率效应。

4) 在试验过程中，铆接结构出现了3种失效模式，即铆钉钉杆剪断失效、铆钉钉头剪断失效、铆接试验件板破裂失效。当加载角度相同时，在一定加载速率范围内，加载速率对铆接结构的失效模式几乎没有影响；加载速率对失效位移存在一定的影响，但仍需考虑不同加载角度引起的不同失效模式。