基于分类算法的人脸识别研究

王欣宇 赵明涛 桂 扬

（安徽财经大学统计与应用数学学院，安徽 蚌埠 233030）

人脸识别主要应用于身份的识别鉴定。随着计算机运行速度的提高，图形识别技术的发展，以及各种统计软件的兴起，面部识别可以更好地实现自动监控与智能预警，在远距离、用户非配合状态下也可以快速确认人员身份。应用快速人脸检测技术可以从监控视频图象中实时查找人脸，并与人脸数据库进行比对，从而实现快速身份识别。现如今人脸识别产品已广泛应用于政府、金融、边检、司法、军队、公安、航天、电力、工厂、教育、医疗等领域，随着技术的进一步成熟和社会认同度的提高，人脸识别技术将应用在更多领域。

国内外在上世纪80年代掀起了对面部识别技术的研究，研究主要集中在面部表情模式、五官线索及文化差异等因素对识别精度的影响。但人脸识别精确度依然存在一些缺点，很多阻碍因素也随之暴露，如不同的年龄、光照水平、背景、姿态等。因此，发展面部识别技术的道路还很漫长。

1.分类算法在面部识别中的应用

分类算法是指通过已有数据集 （训练集）的学习，得到目标函数f（模型），把每个属性集映射到目标属性y（类），且y为离散变量。对于同一个人来说，在无特殊情况下不同时期的照片总存在很大的相似性，然而面容的相似度会随着年龄的变化而逐渐减小，时间越长，面部的差异性就越大，这会对身份的识别造成一系列的困扰。对此，需要建立合理的数学模型。当给出一个人不同时期的面部照片时,通过分类算法来自动识别是否为同一个人，并根据人脸数据库中的数据判断人的身份。在面部识别中，常用的分类算法为Fisher判别分析、神经网络及支持向量机。

2.基于主成分分析降维的Fisher判别分析

2.1 研究思路

为了提高运算效率，更好地比对不同面部照片的相似性，首先对图片进行分块处理，采用主成分分析对图像进行特征提取，找到人脸分布的主成分即脸部图像协方差的特征向量，然后将特征向量转化成“特征脸”，最后利用判别分析识别面部图像，计算新脸的权重集与k个已知人脸权重集的Euclidian距离（即欧式距离），距离最小的即为未知人脸的身份,并通过分类结果得到分类矩阵，计算得到识别正确率。

2.2 研究方法及结果分析

2.2.1 Fisher判别分类原理

Fisher判别分析是将多维数据投影到某个方向上，投影的原则是将总体与总体之间尽可能地分开，再选择合适的判别规则，将新的样品进行分类判别。子空间分析中，给定N个训练数据，样本集合表达为：

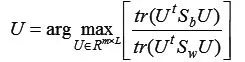
将数据标准化处理，首先将Sw和Sb变形为：

然后运用局部保持思想，分别将Sw和Sb扩展成局部类内散度矩阵和类间散度矩阵，调整和 为：

其中，Aij表示样本 Xi和Xj间的相似度：

2.2.2 特征选取

本文利用Yale人脸数据库进行研究，探究不同的人在不同时期、不同面部表情的情况下面部识别的准确性，以下图所示的六个人的不同照片为例。

图1 部分Yale人脸数据库

为了简化计算过程，减少模拟计算的时间，上述照片均进行过灰度处理，并处理为100*100像素的图片，每个像素点以0-255的灰度值进行表示，0为黑，255为白，值越大越明亮。

由于每张照片有100*100个像素点，也就是10000个变量。由于变量数过大，当采用主成分分析法对变量进行降维处理时，照片数量远远小于变量数，因此需要对变量进行分块处理：对图像形成的灰度矩阵进行列分块，即将每一列作为一个小块，对小块进行降维，再对所有小块中提取的主成分进行二次降维，最终得到少数几个新变量，这些新变量本质上为原始10000个变量的线性组合，具体步骤如表1。

?

由表1可知，当累计贡献率到达90%时，则主成分能够解释的信息量较大，即信息损失量较小，所以初步判定提取累计贡献率达到90%时的主成分，即第一主成分至第四主成分。下面我们绘制碎石图进行直观地分析。

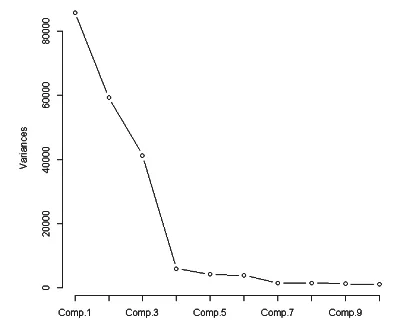
图2 碎石图

在图2中，横坐标为各个主成分，纵坐标为特征值。可以清楚地看到，在第四主成分之前特征值快速减少，第四主成分以后，特征值下降缓慢，故提取前四个主成分进行分析。

得到主成分后我们利用特征值提取图像中的“特征脸”，每一张图像都可以由“特征脸”的线性组合构成。现在我们以一张照片为例，列举出他的原始图像和四张“特征脸”。

图3 原始图像

图4 特征脸

由图4可知，特征脸一（a)与左半脸关系较为紧密，可以表示为左半脸提取出的特征；特征脸二(b)与右半脸关系较为紧密，可以表示为右半脸提取出的特征；特征脸三（c）与脸部中间关系相对紧密，可以表示为脸部中间提取出的特征；特征脸四（d)是整张脸的面部特征，但由于特征值较小，故面部特征图片显示不清楚。

2.2.3 Fisher判别分析

利用上文提取出的主成分，进行Fisher判别分析，首先绘制观测点经过标准化变换后的散点图。

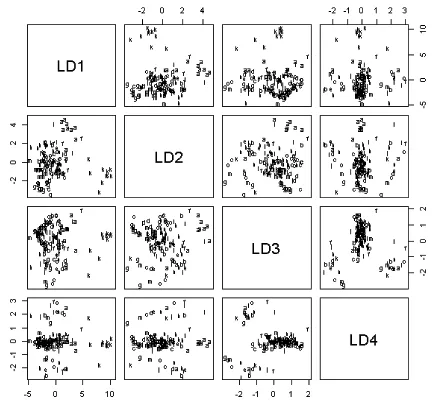
图5 变换后观测点的散点图矩阵

由图5可以看出，k类别和a类别的观测点在各个散点图中，都和其他类别有明显的区别。但是其他13类从直观上来看，难以将其进行区分，所以需要利用量化指标对各个类别进行区分，利用距离因素，得到分类矩阵。

?

表2和表3中，横轴为观测点的预测类别，纵轴为观测点的真实类别。通过表2和表3直观地进行判断，训练样本和测试样本的错判率没有显著差别。计算可知测试样本分类的正确率为53.33%，训练样本分类的正确率为52.67%。

最终通过特征值和特征向量得到判别函数为：

利用判别函数系数，我们得到拟合的图片（图 6）。

图6 拟合图片

可以观察到，拟合图片显示出了原图较多的特征及相似点，拟合效果较好。

3.BP神经网络分类算法

3.1 研究思路

首先提取面部的多个主元，用自相关神经网络将它映射到空间中，再构建一个普通的多层感知器进行判别。然后将像素点输入构建好的BP神经网络进行识别，在隐藏层提取数据的显著特征，并对输入输出层进行非线性转换。最终得到人脸分类结果，并通过结果求得分类矩阵，计算识别正确率。

3.2 研究方法及结果

3.2.1 BP神经网络原理

BP神经网络是目前运用最广泛的神经网络之一，它能学习和储存大量输入及输出模式的映射关系，BP网络结构有 3层：输入层、隐含层、输出层，如图7所示。

图7 神经网络示意图

下面为BP神经网络的具体计算过程。

（1）计算隐含层各神经元的激活值Sj。

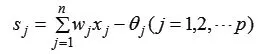
wj为输出层至隐含层的连接权；θj为隐含层的阈值。

（2）计算隐含层j单元的输出值。

阈值θj不断被修改，阈值的作用反应在函数的输出曲线上，如图8所示。

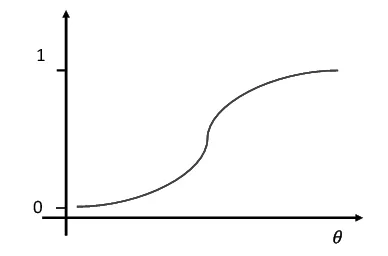
图8 函数输出曲线

可见阈值的作用相当于输出值移动了θ个单位，同理可求出输出端的激活值和输出值。

（3）计算输出层第k个单元的激活值SK。

Vij为隐含层至输出层的全值；θk为输出层单元阈值。

（4）计算实际输出值。

f(Sk)为S型激活函数

（5）纠正各单元误差。

（6）循环记忆训练，得出判别结果。

3.2.2 重要参数说明

输入层神经元数目：在这里输入层中的神经元数目为10000，即为变量数。

隐藏层神经元数目：在这里，根据前面几种方法，并结合隐藏层的特点，我们设置隐藏层神经元数目为5。

输出层神经元数目：在这里输出层神经元数目为15，即为分类数目。

最大迭代数目：基于人脸识别中变量数目较多的特点，我们设置最大迭代数目为150。

3.2.3 BP神经网络模型求解

将上述参数代入模型，构建BP神经网络框架，再将训练样本代入输入层进行迭代，最终可以得到训练好的神经网络模型。将训练样本和测试样本代入模型进行检验和正确率计算，图9为模型的检验。

图9 神经网络检验图

图 9中，由迭代误差图（a)可知，随着迭代次数的增加，迭代拟合误差线和迭代测试误差线不断下降，说明算法不断收敛，误差逐渐减小。在回归误差图（b)中，x轴为目标值，y轴为预测值，最佳拟合线为经过原点，斜率为1的直线，即为图中黑线。图（b)中红线为实际拟合线，红线越接近黑线，则预测结果越好。分析可知，红线和黑线之间偏移量较小，则预测结果较好。由图（c）、（d）ROC曲线图可以看出，训练样本的ROC曲线明显在测试样本ROC曲线上方，说明训练样本预测的准确度高于测试样本，不能只关注训练样本预测的准确率，更重要的是关注测试样本的准确度。

通过编程，可以得到训练样本和测试样本的分类矩阵（神经网络分类矩阵形式与上文中判别分析的分类矩阵形式类似。通过分类矩阵的计算可以看出，测试样本的误判率较高，训练样本的误判率较低。计算可知测试样本分类的正确率为78.26%，训练样本分类的正确率为96.85%。由正确率可知，测试样本分类正确率与训练样本分类正确率有很大差别，训练样本分类正确率远高于测试样本分类正确率，故关注焦点需放在测试样本上。

4.支持向量机算法构建人脸识别模型

4.1 研究思路

基于支持向量机空间变换的特点，提取图像的奇异值，将数据分布在二维平面内，并通过内积函数，在高维空间内确立最优分类超平面，以最大间隔将数据分开，最后得到人脸分类结果，并获取分类矩阵，计算识别正确率。

4.2 研究方法及结果分析

4.2.1 多分类支持向量机原理

多分类支持向量机的基本思想是将多分类思想转化为多个二分类问题，即将K类转化为K个二分类问题。如有5类，将1类作为正类，其余4类作为负类，然后再取1类作为正类，其余4类为负类，共做5次二分类问题。判断类别方法是将最后若干个分类器完成后，将新的样本输入每一个建好的分类器中去，最后以投票的方式，把样本得到的票数最多的类别作为他的预测值。

4.2.2 求解过程

支持向量机训练的步骤如下：

（2）选择适当的核函数类型。

（3）利用二次规划方法求解如下公式最优解，得到支持向量及最优Lagrange乘子a*。

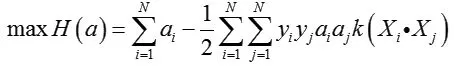
（4）利用样本库中的一个支持向量X，带入以下公式：

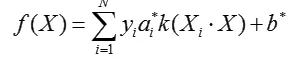
可得到偏差值b*。

支持向量机的分类步骤如下：

（1）输入待测样品X。

（2）利用训练好的 Lagrange乘子 a*、偏差值b*和核函数，求解判别函数f(X)。

（3）根据 sgn(f(X))的值，输出类别。如果 sgn(f(X))为-1，则该样品属于类 w1；如果 sgn(f(X))为1，则该样品属于类w2。

通过编程求解，得到支持向量机的分类矩阵。通过分类矩阵的计算可以看出测试样本与训练样本都有较低的误错判率。计算可知测试样本分类的正确率为93.33%，训练样本分类的正确率为100%。由正确率可知，测试样本分类的正确率与训练样本分类的正确率均极高。

5.三种分类算法的比较

5.1 研究思路

计算Fisher判别、BP神经网络和支持向量机这三种模型的正确率，并进行比较分析，最终得出最优模型。

5.2 结果分析

表4为各个分类算法的正确率。

?

由表4可知，支持向量机和BP神经网络在训练样本和测试样本的准确率上远远大于Fisher判别分析；在测试样本正确率上支持向量机仍保持较高的正确率，而BP神经网络的正确率则大幅衰减，说明支持向量机在人脸识别上有较为优越的表现，有进一步研究及推广的价值，而Fisher判别分析和BP神经网络在人脸识别上则有较大的改进空间。

6.总结

本文通过Fisher判别分析、BP神经网络及支持向量机三种分类算法构建不同人脸识别模型，并给出三种模型识别人脸的正确率，便于直接比较三种算法应用在人脸识别中的优缺点，找出最佳人脸识别模型。在利用Fisher判别分析进行人脸识别模型的构建时，首先对图片进行分块处理，并利用主成分分析对影响人像差异的向量空间进行降维处理；最后运用Fisher判别分析求解判别函数，判别未知人脸的身份，并检验模型的识别准确率。在依托神经网络进行人脸识别模型的构建时，首先提取面部的多个主元，用自相关神经网络将面部主元映射到空间中，并将像素点输入到构建好的神经网络中，提取数据的显著特征；然后对输入输出层进行非线性转化，得到最终人脸识别结果，并检验识别准确率。在构建支持向量机进行人脸识别模型时，首先提取人像图片的奇异值；然后通过核函数，利用最大间隔将数据分类，得到分类结果，并检验识别准确率；最后，比较不同模型预测的正确率大小，选择最优的面部识别模型。但是由于水平和时间有限，本文没有对支持向量机进行过多的描述。针对这个问题，我们将进行后续研究，深入探讨支持向量机在模式识别特别是人脸识别上的作用。